1. Basic algorithm

Quick sort O ( n log ⁡ n ) O(n \log n) O(nlogn)

void quick_sort(int a[], int l, int r)
{
    if(l >= r) return;
    
    int x = a[(l+r)>>1], i = l-1, j = r+1;
    while(i < j) {
        do i++; while(a[i] < x);
        do j--; while(a[j] > x);
        if(i < j) swap(a[i],a[j]);
    }
    quick_sort(a,l,j);
    quick_sort(a,j+1,r);
}

Merge sort O ( n log ⁡ n ) O(n\log n) O(nlogn)

void merge_sort(int a[], int l, int r)
{
    if(l >= r) return;

    int mid = l+r>>1;
    merge_sort(a,l,mid);
    merge_sort(a,mid+1,r);

    int k = 0, i = l, j = mid+1;
    while(i <= mid && j <= r) {
        if(a[i] <= a[j]) tmp[k++] = a[i++];
        else tmp[k++] = a[j++];
    }

    while(i <= mid) tmp[k++] = a[i++];
    while(j <= r) tmp[k++] = a[j++];

    for(int x = 0, y = l;y <= r;x++, y++) a[y] = tmp[x];

}

Dichotomy algorithm O ( log ⁡ n ) O(\log n) O(logn)

Integer bisection algorithm

bool check(int x)	// Check whether x satisfies a certain property
{
    
}

// Used when the interval [l,r] is divided into [l,mid] and [mid+1,r]

int binary_search(int l, int r)
{
    while(l < r)
    {
        int mid = (l+r)>>1;
        if(check(mid)) r = mid;
        else l = mid+1;
    }
    return l;
}

Floating point binary algorithm

const double eps = 1e-6;

bool check(double x) // Check whether x satisfies a certain property
{
    
}

double binary_search(double l, double r)
{
    while(r-l > eps)
    {
        double mid = (l+r)>>1;
        if(check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

high-precision O ( n ) O(n) O(n)

addition

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

subtraction

// C = A - B, satisfying a > = B, a > = 0, b > = 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

multiplication

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

division

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

Prefix and O ( n ) O(n) O(n) initialization O ( 1 ) O(1) O(1) query prefix and

One dimensional prefix sum

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

Binary prefix sum

S[i, j] = The first i that 's ok j The sum of all elements in the upper left part of the column grid
//The sum of submatrixes with (x1, y1) as the upper left corner and (x2, y2) as the lower right corner is:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

Difference O ( n ) O(n) O(n)

One dimensional difference

Give interval[l, r]Each number in the plus c: B[l] += c, B[r + 1] -= c

Two dimensional difference

Give(x1, y1)Is the upper left corner,(x2, y2)Add to all elements in the submatrix in the lower right corner c: 
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

Bit operation

seek n The first k Digit number: n >> k & 1
 return n Last 1: lowbit(n) = n & -n

Double pointer O ( n ) O(n) O(n)

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // Logic of specific problems
}
Classification of frequently asked questions:
    (1) For a sequence, maintain an interval with two pointers
    (2) For two sequences, maintain a certain order, such as merging two ordered sequences in merge sort

799. Longest continuous non repetitive subsequence - AcWing question bank

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-lmzmjkae-1629167397783) (C: / users / Dell / appdata / roaming / typora user images / image-20210628145907363. PNG)]

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+50;
int a[MAXN], cnt[MAXN], dis[MAXN];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    int ans = 1;
    for(int i = 1,j = 1;j <= n;j++)
    {
        cnt[a[j]]++;
        if(cnt[a[j]] > 1) {
            for(int k = i;k <= dis[a[j]];k++) {
                cnt[a[k]]--;
            }
            i = dis[a[j]]+1;
        }
        dis[a[j]] = j;
        ans = max(ans,j-i+1);
    }
    printf("%d\n",ans);
    return 0;
}

AcWing 800. Target and of array elements - acwing

#include<iostream>
using namespace std;
const int N=100010;
int a[N],b[N];
int main()
{
    int n,m,x;
    cin>>n>>m>>x;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<m;i++) cin>>b[i];
    for(int i = 0, j = m-1;i < n;i++)
    {
        while(j >= 0 && a[i] + b[j] > x) j--;
        if(a[i] + b[j] == x) {
            printf("%d %d\n",i,j);
            return 0;
        }
    }
    return 0;
}

Discretization O ( log ⁡ n ) O(\log n) O(logn)

vector<int> alls; // Store all values to be discretized
sort(alls.begin(), alls.end()); // Sort all values
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // Remove duplicate elements

// Find the discrete value corresponding to x
int find(int x) // Find the first position greater than or equal to x
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // Map to 1, 2 n
}

802. Interval sum - AcWing question bank

#include<bits/stdc++.h>
using namespace std;

typedef pair<int,int> PII;
const int MAXN = 3e5+50;
int n, m;
int a[MAXN], sum[MAXN];

vector<int>all;
vector<PII>add, query;

int find(int x)
{
    int l = 0, r = all.size()-1;

    while(l < r)
    {
        int mid = (l + r) >> 1;
        if(all[mid] >= x) r = mid;
        else l = mid+1;
    }
    return r+1;
}

vector<int>::iterator unique(vector<int> &a)
{
    int j = 0;
    for(int i = 0;i < a.size();i++)
    {
        if(!i && a[i] != a[i-1])
        {
            a[j++] = a[i];
        }
    }
    return a.begin()+j;
}

int main()
{
    scanf("%d%d",&n,&m);
    while(n--)
    {
        int x, c;
        scanf("%d%d",&x,&c);
        add.push_back({x,c});
        all.push_back(x);
    }

    while(m--)
    {
        int l, r;
        scanf("%d%d",&l,&r);
        query.push_back({l,r});
        all.push_back(l);
        all.push_back(r);
    }

    sort(all.begin(),all.end());
    all.erase(unique(all.begin(),all.end()),all.end());

    for(auto it : add)
    {
        int u = find(it.first);
        a[u] += it.second;
    }

    for(int i = 1;i <= all.size();i++)
    {
        sum[i] = sum[i-1]+a[i];
    }

    for(auto it : query)
    {
        int l = find(it.first);
        int r = find(it.second);
        int res = sum[r]-sum[l-1];
        printf("%d\n",res);
    }

    return 0;
}

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int MAXN = 3e5 + 50;
int a[MAXN], sum[MAXN];

vector<int>all;
vector<PII>add, query;
int x, c;

int main()
{
    int n, m;
    scanf("%d%d",&n,&m);
    while(n--)
    {
        scanf("%d%d",&x,&c);
        add.push_back({x,c});
        all.push_back(x);
    }

    while(m--)
    {
        int l, r;
        scanf("%d%d",&l,&r);
        query.push_back({l,r});
        all.push_back(l);
        all.push_back(r);
    }

    sort(all.begin(),all.end());
    all.erase(unique(all.begin(),all.end()),all.end());

    for(auto it : add)
    {
        int u = lower_bound(all.begin(),all.end(),it.first)-all.begin();
        a[u] += it.second;
    }

    for(int i = 1;i <= all.size();i++)
    {
        sum[i] = sum[i-1] + a[i];
    }

    for(auto it : query)
    {
        int l = lower_bound(all.begin(),all.end(),it.first)-all.begin();
        int r = lower_bound(all.begin(),all.end(),it.second)-all.begin();
        int ans = sum[r]-sum[l-1];
        printf("%d\n",ans);
    }

}

Interval merging

// Merge all intersecting intervals
void merge(vector<PII> &segs)
{
    vector<PII> res;

    sort(segs.begin(), segs.end());

    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        if (ed < seg.first)
        {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);

    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}

Left endpoint sort

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 1e5+40;

struct node{
    int l, r;
    friend bool operator<(node &a, node b)
    {
        return a.l < b.l;
    }
};

vector<node>N;

int main()
{
    int n;
    scanf("%d",&n);
    int re = n;
    while(n--)
    {
        int l, r;
        scanf("%d%d",&l,&r);
        N.push_back({l,r});
    }
    sort(N.begin(),N.end());

    int cnt = 1;
    int ir = N[0].r;
    for(int i = 1;i < re;i++)
    {
        if(N[i].l > ir) {
            cnt++;
            ir = N[i].r;
        }
        else ir = max(ir,N[i].r);
    }
    printf("%d\n",cnt);
    return 0;
}

2. Data structure

C++STL

vector, Variable length array, multiplication idea
    size()  Returns the number of elements
    empty()  Returns whether it is empty
    clear()  empty
    front()/back()
    push_back()/pop_back()
    begin()/end()
    []
    Support comparison operation, in dictionary order

pair<int, int>
    first, First element
    second, Second element
    Support comparison operation to first Is the first keyword to second Is the second keyword (dictionary order)

string，character string
    size()/length()  Return string length
    empty()
    clear()
    substr(Starting subscript,(Substring length))  Return substring
    c_str()  Returns the starting address of the character array where the string is located

queue, queue
    size()
    empty()
    push()  Insert an element at the end of the queue
    front()  Returns the queue header element
    back()  Return end of queue element
    pop()  Pop up queue header element

priority_queue, Priority queue. The default is large root heap
    size()
    empty()
    push()  Insert an element
    top()  Returns the top of heap element
    pop()  Pop top element
    How to define as a small root heap: priority_queue<int, vector<int>, greater<int>> q;

stack, Stack
    size()
    empty()
    push()  Insert an element to the top of the stack
    top()  Return stack top element
    pop()  Pop up stack top element

deque, Double ended queue
    size()
    empty()
    clear()
    front()/back()
    push_back()/pop_back()
    push_front()/pop_front()
    begin()/end()
    []

set, map, multiset, multimap, Based on balanced binary tree (red black tree), the ordered sequence is maintained dynamically
    size()
    empty()
    clear()
    begin()/end()
    ++, -- Return precursor and successor, time complexity O(logn)

    set/multiset
        insert()  Insert a number
        find()  Find a number
        count()  Returns the number of a number
        erase()
            (1) The input is a number x，Delete all x   O(k + logn)
            (2) Enter an iterator and delete it
        lower_bound()/upper_bound()
            lower_bound(x)  Return greater than or equal to x Iterator of the smallest number of
            upper_bound(x)  Return greater than x Iterator of the smallest number of
    map/multimap
        insert()  The number of inserts is one pair
        erase()  The input parameter is pair Or iterator
        find()
        []  be careful multimap This operation is not supported. The time complexity is O(logn)
        lower_bound()/upper_bound()

unordered_set, unordered_map, unordered_multiset, unordered_multimap, Hashtable 
    Similar to the above, the time complexity of adding, deleting, modifying and querying is O(1)
    I won't support it lower_bound()/upper_bound()， Iterator++，--

bitset, Pressure level
    bitset<10000> s;
    ~, &, |, ^
    >>, <<
    ==, !=
    []

    count()  Returns how many 1s there are

    any()  Determine whether there is at least one 1
    none()  Judge whether all are 0

    set()  Set all positions to 1
    set(k, v)  Will be the first k Bit becomes v
    reset()  Change all bits to 0
    flip()  Equivalent to~
    flip(k) Put the first k Bit inversion

Double linked list O ( n ) O(n) O(n)

// e [] represents the value of the node, l [] represents the left pointer of the node, r [] represents the right pointer of the node, and idx represents which node is currently used
int e[N], l[N], r[N], idx;

// initialization
void init()
{
    //0 is the left endpoint and 1 is the right endpoint
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// Insert a number x to the right of node a
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// Delete node a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

Monotone stack O ( n ) O(n) O(n)

Ensure that the top element of the stack is the largest / smallest in the stack.

Common model: find out that the nearest one on the left of each number is larger than it/Small number
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

830. Monotone stack - AcWing question bank

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 1e5+50;
int stk[MAXN], a[MAXN];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 0;i < n;i++) scanf("%d",&a[i]);
    int tt = 0;
    for(int i = 0;i < n;i++)
    {
        while(tt && a[i] <= stk[tt-1])
        {
            tt--;
        }
        if(tt == 0) printf("-1%c", n == 0 ? '\n' : ' ');
        else printf("%d%c",stk[tt-1],n == 0 ? '\n' : ' ');
        stk[tt++] = a[i];
    }
    //printf("\n");
    return 0;
}

Monotone queue O ( n ) O(n) O(n)

Common model: find the maximum value in the sliding window/minimum value
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // Judge team leader, hh++
    while (hh <= tt && check(q[tt], i)) tt -- ;  // Judge whether the tail of the team is monotonous, tt--
    q[ ++ tt] = i;
}

154. Sliding window - AcWing question bank

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e6+50;
int a[MAXN];
deque<int>q1,q2;

int main()
{
    int n, k;
    scanf("%d%d",&n,&k);
    for(int i = 0;i < n;i++) scanf("%d",&a[i]);

    for(int i = 0;i < k;i++)
    {
        while(!q1.empty() && a[i] <= a[q1.back()]) q1.pop_back();
        q1.push_back(i);
    }
    printf("%d ",a[q1.front()]);

    for(int i = k;i < n;i++)
    {
        while(!q1.empty() && a[i] <= a[q1.back()]) q1.pop_back();
        while(!q1.empty() && i - q1.front() + 1 > k) q1.pop_front();
        q1.push_back(i);
        printf("%d ",a[q1.front()]);
    }

    printf("\n");

    for(int i = 0; i < k;i++)
    {
        while(!q2.empty() && a[i] >= a[q2.back()]) q2.pop_back();
        q2.push_back(i);
    }
    printf("%d ",a[q2.front()]);
    for(int i = k;i < n;i++)
    {
        while(!q2.empty() && a[i] >= a[q2.back()]) q2.pop_back();
        while(!q2.empty() && i - q2.front() + 1 > k) q2.pop_front();
        q2.push_back(i);
        printf("%d ",a[q2.front()]);
    }
    printf("\n");

    return 0;
}

Handwritten monotone queue

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;
const int MAXN = 1e6+50;
int n, k;
int a[MAXN], q[MAXN];

int main()
{
    scanf("%d%d",&n,&k);
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    int hh = 0, tt = -1; // hh is the head and tt is the tail
    for(int i = 1;i <= n;i++)
    {
        while(hh <= tt && i - q[hh] + 1 > k) hh++;
        while(hh <= tt && a[i] <= a[q[tt]]) tt--;
        q[++tt] = i;
        if(i >= k) printf("%d ",a[q[hh]]);
    }
    printf("\n");
    hh = 0, tt = -1;
    for(int i = 1;i <= n;i++)
    {
        while(hh <= tt && i - q[hh] + 1 > k) hh++;
        while(hh <= tt && a[i] >= a[q[tt]]) tt--;
        q[++tt] = i;
        if(i >= k) printf("%d ",a[q[hh]]);
    }
    printf("\n");
    return 0;
}

KMP O ( n ) O(n) O(n)

// s [] is the long text, p [] is the pattern string, n is the length of s, and m is the length of p
 Find the of pattern string Next Array:
for (int i = 2, j = 0; i <= m; i ++ )
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

// matching
for (int i = 1, j = 0; i <= n; i ++ )
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        // Logic after successful matching
    }
}

831. KMP string - AcWing question bank

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e6+50;
int ne[MAXN];
char p[MAXN], s[MAXN];
int n, m;

int main()
{
    cin >> n;
    cin >> p+1;
    cin >> m;
    cin >> s+1;

    for(int i = 2, j = 0;i <= n;i++)
    {
        while(j && p[i] != p[j+1]) j = ne[j];
        if(p[i] == p[j+1]) j++;
        ne[i] = j;
    }

    for(int i = 1, j = 0;i <= m;i++)
    {
        while(j && s[i] != p[j+1]) j = ne[j];
        if(s[i] == p[j+1]) j++;
        if(j == n)
        {
            j = ne[j];
            printf("%d ",i-n);
        }
    }
    printf("\n");

    return 0;
}

String hash

Core idea: regard string as P Hexadecimal number, P The empirical value of is 131 or 13331, and the conflict probability of taking these two values is low
 Tip: use 2 for modulo numbers^64，Use it directly unsigned long long The result of overflow is the result of modulo

typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k] stores the hash value of the first k letters of the string, and p[k] stores P^k mod 2^64

// initialization
void init()
{
	p[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
}

// Calculate the hash value of substring str[l ~ r]
ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

841. String hash - AcWing question bank

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+50;
const int P = 131;
char str[MAXN];

int n, m;
typedef unsigned long long ULL;
ULL h[MAXN], p[MAXN]; // h[k] stores the hash value of the first k letters of the string, and p[k] stores P^k mod 2^64

// initialization
void init()
{
	p[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
}

// Calculate the hash value of substring str[l ~ r]
ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    scanf("%d%d",&n,&m);
    scanf("%s",str+1);
    init();
    while(m--)
    {
        int l1, r1, l2, r2;
        scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
        if(get(l1,r1) == get(l2,r2)) puts("Yes");
        else puts("No");
    }
    return 0;
}

Joint search set O ( n log ⁡ n ) O(n \log n) O(nlogn)

(1)Simple parallel search set:

    int p[N]; //Store the ancestor node of each point

    // Returns the ancestor node of x
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // Initialization, assuming that the node number is 1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // Merge the two sets of a and b:
    p[find(a)] = find(b);


(2)maintain size Consolidated query set:

    int p[N], size[N];
    //p [] stores the ancestral node of each point. size [] only the meaningful of the ancestral node, indicating the number of points in the set of ancestral nodes

    // Returns the ancestor node of x
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // Initialization, assuming that the node number is 1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // Merge the two sets of a and b:
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);

837. Number of points in connected blocks - AcWing question bank

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+50;
int fa[MAXN], sz[MAXN];

int find(int x)
{
    if(x != fa[x]) fa[x] = find(fa[x]);
    return fa[x];
}

int main()
{
    int n, m;
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++)
    {
        fa[i] = i;
        sz[i] = 1;
    }
    while(m--)
    {
        string op;
        int a, b;
        cin >> op;
        if(op == "Q2")
        {
            scanf("%d",&a);
            a = find(a);
            printf("%d\n",sz[a]);
        }
        else if(op == "Q1")
        {
            scanf("%d%d",&a,&b);
            if(find(a) == find(b)) puts("Yes");
            else puts("No");
        }
        else
        {
            scanf("%d%d",&a,&b);
            a = find(a);
            b = find(b);
            if(a != b)
            {
                fa[a] = b;
                sz[b] += sz[a];
            }
            
        }
    }
    return 0;
}

Trie tree O ( n ) O(n) O(n)

int son[N][26], cnt[N], idx = 0;
// Point 0 is both a root node and an empty node
// son [] [] stores the child nodes of each node in the tree
// cnt [] stores the number of words that end with each node

// Insert a string
void insert(string str)
{
    int p = 0;
    for(int i = 0;str[i] != '\0';i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p]++;
}

// The number of occurrences of the query string
int query(string str)
{
    int p = 0;
    for(int i = 0;str[i] != '\0';i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

835. Trie string Statistics - AcWing question bank

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e5+50;
char s[MAXN];
int cnt[MAXN], son[MAXN][28];
int idx = 0;


void insert(string str)
{
    int p = 0;
    for(int i = 0;str[i] != '\0';i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p]++;
}

int query(string str)
{
    int p = 0;
    for(int i = 0;str[i] != '\0';i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        string op;
        cin >> op;
        if(op == "I")
        {
            string s;
            cin >> s;
            insert(s);
        }
        else {
            string s;
            cin >> s;
            printf(
                "%d\n",query(s));
        }
    }
    return 0;
}

143. Maximum XOR pair - AcWing question bank

Maximum XOR sum

Given a sequence, find the XOR maximum of two elements in the sequence.

Dictionary tree optimization O ( n l o g n ) O(nlogn) O(nlogn)

Each time you go in the opposite direction to the current bit, ensure XOR and maximum.

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;
const int MAXN = 1e5+50;
int n, a[MAXN], son[MAXN*30][2], idx;

void insert(int x)
{
    int p = 0;
    for(int i = 30;i >= 0;i--)
    {
        int u = x >> i & 1;
        if(!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
    }
}

int query(int x)
{
    int p = 0, res = 0;
    for(int i = 30;i >= 0;i--)
    {
        int u = x >> i & 1;
        if(son[p][!u]) {
            p = son[p][!u];
            res += 1 << i;
        }
        else p = son[p][u];
    }
    return res;
}

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)
    {
        scanf("%d",&a[i]);
        insert(a[i]);
    }
    int res = 0;
    for(int i = 1;i <= n;i++) res = max(res,query(a[i]));
    printf("%d\n",res);
    
    return 0;
}

Joint search set

• Merge two sets
• Query the ancestor node of an element
• Ask if two elements are in the same collection

// Simple parallel search set:

int p[N]; //Store the ancestor node of each point

// Return the ancestor node of x + path compression
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// Initialization, assuming that the node number is 1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;

// Merge the two sets of a and b:
p[find(a)] = find(b);

Optimization mode

• Path compression O ( log ⁡ n ) O(\log n) O(logn)
• Merge by rank O ( log ⁡ n ) O(\log n) O(logn)
• Both O ( α ( n ) ) O(\alpha(n)) O(α(n))

Weighted union search set

• Record the size of each collection and bind it to the root node
• The distance (relative distance) from each node to the root node is bound to each element

// Maintain and query the set size:

int p[N], size[N];
//p [] stores the ancestral node of each point. size [] only the meaningful of the ancestral node, indicating the number of points in the set of ancestral nodes

// Returns the ancestor node of x
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// Initialization, assuming that the node number is 1~n
for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    size[i] = 1;
}

// Merge the two sets of a and b:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);

// Maintain the distance to the ancestral node and query the set:

int p[N], d[N];
//P [] stores the ancestor node of each point, and d[x] stores the distance from X to p[x]

// Returns the ancestor node of x
int find(int x)
{
    if (p[x] != x)
    {
        int root = find(p[x]);
        d[x] += d[p[x]];
        p[x] = root;
    }
    return p[x];
}

// Initialization, assuming that the node number is 1~n
for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    d[i] = 0;
}

// Merge the two sets of a and b:
p[find(a)] = find(b);
d[find(a)] = distance; // Initialize the offset of find(a) according to the specific problem

Expand domain and query set (enumeration)

1250. Grid game - AcWing question bank

Parallel set search solves the problems of connectivity (undirected graph connectivity component) and transitivity (genealogical relationship), and can be maintained dynamically. Regardless of the lattice, an edge is added to any graph to form a ring. If and only if the two points connected by this edge have been connected, the points can be divided into several sets, and each set corresponds to a connected block in the graph.

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;

const int MAXN = 40050;
int n, m, res = 1e9;
int a[MAXN], fa[MAXN];

int transfer(int x, int y)	// Convert 2D to 1D
{
    return (x-1) * n + y;
}

void init()
{
    for(int i = 1;i <= n*n;i++)
    {
        fa[i] = i;
    }
}

int find(int x)
{
    if(x != fa[x]) fa[x] = find(fa[x]);
    return fa[x];
}

int main()
{
    scanf("%d%d",&n,&m);
    init();
    for(int i = 1;i <= m;i++)
    {
        int x, y;
        char op;
        scanf("%d %d %c",&x,&y,&op);
        int res1, res2;
        
        res1 = transfer(x,y);
        if(op == 'D') res2 = transfer(x+1,y);
        else if(op == 'R') res2 = transfer(x,y+1);
        
        int u = find(res1), v = find(res2);
        if(u == v) {
            res = min(res,i);
        }
        else {
            fa[u] = v;
        }
    }
    if(res != 1e9) printf("%d\n",res);
    else puts("draw");
    return 0;
}

1252. Matching purchase - AcWing question bank

Combined search + 01 Backpack

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;
const int MAXN = 10010;
int fa[MAXN], c[MAXN], d[MAXN], dp[MAXN];
int n, m, w, id;

struct node{
    int c, d;
}Node[MAXN];

int find(int x)
{
    if(x != fa[x]) fa[x] = find(fa[x]);
    return fa[x];
}

void init()
{
    for(int i = 1;i <= n;i++) fa[i] = i;
}

int main()
{
    scanf("%d%d%d",&n,&m,&w);
    init();
    for(int i = 1;i <= n;i++)
    {
        scanf("%d%d",&c[i],&d[i]);
    }
    for(int i = 1;i <= m;i++)
    {
        int a, b;
        scanf("%d%d",&a,&b);
        int u = find(a), v = find(b);
        
        if(u != v)
        {
            fa[v] = u;
            c[u] += c[v];
            d[u] += d[v];
        }
    }
    
    for(int i = 1;i <= n;i++) {
        if(i == fa[i])
        {
            Node[id].c = c[i];
            Node[id].d = d[i];
            id++;
        }
    }
    
    for(int i = 0;i < id;i++)
    {
        for(int j = w;j >= Node[i].c;j--)
        {
            dp[j] = max(dp[j],dp[j-Node[i].c]+Node[i].d);
        }
    }
    int ans = dp[w];
    printf("%d\n",ans);
    return 0;
}

237. Automatic program analysis - AcWing question bank

Joint search set + discretization

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;
typedef long long ll;
const int MAXN = 2e6+50;

int n, T, id, cnt;
int fa[MAXN];

vector<pair<int,int>>equ, iequ;

int all[MAXN];

void init()
{
    for(int i = 0;i <= cnt;i++) fa[i] = i;
}

int search(int x)
{
    int res = lower_bound(all,all+cnt,x)-all;
    return res;
}

int find(int x)
{
    if(x != fa[x]) fa[x] = find(fa[x]);
    return fa[x];
}

int main()
{
    scanf("%d",&T);
    while(T--)
    {
        equ.clear();
        iequ.clear();
        bool flag = true;
        scanf("%d",&n);
        for(int k = 0;k < n;k++)
        {
            int i, j, e;
            scanf("%d%d%d",&i,&j,&e);
            if(e == 1) equ.push_back(make_pair(i,j));
            else iequ.push_back(make_pair(i,j));
            all[id++] = i;
            all[id++] = j;
        }
        sort(all,all+id);
        cnt = unique(all,all+id)-all;
        init();
        for(auto i : equ)
        {
            int x = search(i.first), y = search(i.second);
            int u = find(x), v = find(y);
            fa[u] = v;
        }
        for(auto i : iequ)
        {
            int x = search(i.first), y = search(i.second);
            int u = find(x), v = find(y);
            if(u == v) {
                flag = false;
                break;
            }
        }
        if(flag) puts("YES");
        else puts("NO");
    }
    return 0;
}

Tree array

Basic principles

• Quick prefix sum O ( log ⁡ n ) O(\log n) O(logn)
• Modify a number O ( log ⁡ n ) O(\log n) O(logn)

Based on binary optimization

x = 2 i k + 2 i k = 1 + 2 i k − 2 + ⋯ + 2 i 1 log ⁡ x ≥ i k ≥ i k − 1 ≥ i k − 2 ≥ ⋯ ≥ i 1 x = 2^{i_k}+2^{i_{k=1}}+2^{i_{k-2}}+\dots +2^{i_1} \qquad \qquad \log x \ge i_k \ge i_{k-1} \ge i_{k-2} \ge \dots \ge i_1 x=2ik​+2ik=1​+2ik−2​+⋯+2i1​logx≥ik​≥ik−1​≥ik−2​≥⋯≥i1​

① ( x − 2 i 1 , x ] (x-2^{i_1},x] (x−2i1​,x]

② ( x − 2 i 1 − 2 i 2 , x − 2 i 1 ] (x-2^{i_1}-2^{i_2},x-2^{i_1}] (x−2i1​−2i2​,x−2i1​]

③ ( x − 2 i 1 − 2 i 2 − 2 i 3 , x − 2 i 1 − 2 i 2 ] (x-2^{i_1}-2^{i_2}-2^{i_3},x-2^{i_1}-2^{i_2}] (x−2i1​−2i2​−2i3​,x−2i1​−2i2​]

... \dots ...

k ( x − 2 i 1 − 2 i 2 − ⋯ − 2 i k = 0 , x − 2 i 1 − 2 i 2 − ⋯ − 2 i k − 1 ] (x-2^{i_1}-2^{i_2}-\dots -2^{i_k} = 0,x-2^{i_1}-2^{i_2}-\dots -2^{i_{k-1}}] (x−2i1​−2i2​−⋯−2ik​=0,x−2i1​−2i2​−⋯−2ik−1​]

Discovery interval ( L , R ] (L,R] The interval length of (L,R] is the power corresponding to the last bit 1 of R binary l o w b i t ( R ) lowbit(R) lowbit(R)

Interval is [ R − l o w b i t ( R ) + 1 , R ] [R-lowbit(R)+1,R] [R−lowbit(R)+1,R]

remember c [ x ] c[x] c[x] is interval a [ x − l o w b i t ( x ) + 1 , x ] a[x-lowbit(x)+1,x] a[x − lowbit(x)+1,x] sum of all numbers

c i = a i + a i − 1 + ... ... + a i − l o w b i t ( i ) + 1 c_i = a_i+a_{i-1}+......+a_{i-lowbit(i)+1} ci​=ai​+ai−1​+......+ai−lowbit(i)+1​

c[1] = a[1]

c[2] = a[2]+a[1]

c[3] = a[3]

c[4] = a[4]+a[3]+a[2]+a[1]

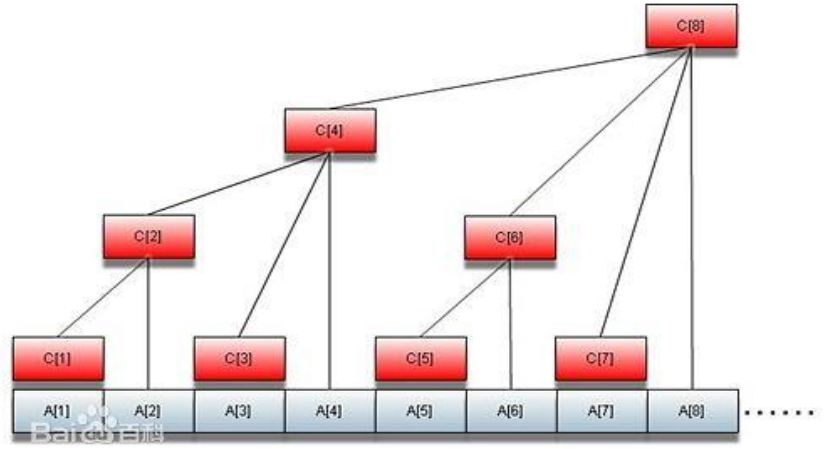
Tree array query O ( log ⁡ n ) O(\log n) O(logn)

eg query a[1]+a[2] +... + a[7]

a[7] = c[7] a[6]+a[5] = c[6] a[4]+a[3]+a[2]+a[1] = c[4]

7 = ( 111 ) 2 (111)_2 (111)2​ 6 = ( 110 ) 2 (110)_2 (110)2​ 4 = ( 100 ) 2 (100)_2 (100) 2 * subtract lowbit each time

// Sum of query a[1~x]
int sum(int x)
{
    int ret = 0;
    while(x)
    {
        ret += c[x];
        x -= lowbit(x);
    }
    return ret;
}

Tree array modification O ( log ⁡ n ) O(\log n) O(logn)

The parent node of X is x+lowbit(x)

Each modification will affect this node to the node under the root path

// a[i] += k
void change(int i, int k)
{
    while(i <= n)
    {
        c[i] += k;
        i += lowbit(i);
    }
}

lowbit(i) solution

inline int lowbit(int x)
{
    return x & (-x);
}

inline int lowbit(int x)
{
    return x & (-x);
}

// Sum of query a[1~x]
int sum(int x)
{
    int ret = 0;
    while(x)
    {
        ret += c[x];
        x -= lowbit(x);
    }
    return ret;
}

// a[i] += k
void change(int i, int k)
{
    while(i <= n)
    {
        c[i] += k;
        i += lowbit(i);
    }
}

extend

Interval modification and single point query

• a [ L , R ] a[L,R] Each element in a[L,R] + c
• seek a [ x ] a[x] What is a[x]

Using differential array + tree array

Interval modification is equivalent to modifying two points in the difference array

Single point query is equivalent to the prefix sum of difference fraction group

Interval modification and interval summation

Interval modification: differential array a [ L , R ] + = c a[L,R] += c a[L,R]+=c is equivalent to b [ R + 1 ] − = c b [ L ] − = c b[R+1] -= c \qquad b[L] -= c b[R+1]−=cb[L]−=c

Interval summation: a [ 1 ] + a [ 2 ] + a [ 3 ] + ⋯ + a [ x ] a[1]+a[2]+a[3]+\dots+a[x] a[1]+a[2]+a[3]+⋯+a[x] = ∑ i = 1 x a [ i ] = ∑ i = 1 x ∑ j = 1 i b [ j ] \sum_{i=1}^xa[i] = \sum_{i=1}^{x} \sum_{j=1}^i b[j] ∑i=1x​a[i]=∑i=1x​∑j=1i​b[j]

Consider complement

a [ 1 ] + a [ 2 ] + a [ 3 ] + ⋯ + a [ x ] = ( x + 1 ) ∗ ( b [ 1 ] + b [ 2 ] + ⋯ + b [ x ] ) − ( 1 ∗ b [ 1 ] + 2 ∗ b [ 2 ] + 3 ∗ b [ 3 ] + ⋯ + x ∗ b [ x ] ) a[1]+a[2]+a[3]+\dots+a[x] = (x+1)*(b[1]+b[2]+\dots+b[x])-(1*b[1]+2*b[2]+3*b[3]+\dots+x*b[x]) a[1]+a[2]+a[3]+⋯+a[x]=(x+1)∗(b[1]+b[2]+⋯+b[x])−(1∗b[1]+2∗b[2]+3∗b[3]+⋯+x∗b[x])

Front is b [ i ] b[i] Prefix and of b[i], followed by i ∗ b [ i ] i*b[i] Prefix and of I * b[i]

Two dimensional tree array

// a[x][y] += z;
int update(int x, int y, int z)
{
    int i = x;
    while(i <= n)
    {
        int j = y;
        while(j <= m)
        {
            c[i][j] += z;
            j += lowbit(j);
        }
        i += lowbit(i);
    }
}

// a[1][1] + ...... + a[1][y] + a[2][1] + ...... a[2][n] + ...... +a[x][1] + ...... + a[x][y]
int sum(int x, int y)
{
    int res = 0, i = x;
    while(i > 0)
    {
        j = y;
        while(j > 0)
        {
            res += c[i][j];
            j -= lowbit(j);
        }
        i -= lowbit(i);
    }
    return res;
}

Segment tree

A complete binary tree, each node represents an interval.

section [ L , R ] [L,R] [L,R] is divided into [ L , m i d ] , [ m i d + 1 , R ] [L,mid],[mid+1,R] [L,mid],[mid+1,R] m i d = ⌊ L + R 2 ⌋ mid = \lfloor \frac{L+R}{2} \rfloor mid=⌊2L+R​⌋

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-ahksiy0k-1629167397787) (C: / users / Dell / appdata / roaming / typora user images / image-20210322084255533. PNG)]

Current node x of line segment tree

Parent node ⌊ x 2 ⌋ \lfloor \frac{x}{2} \rfloor ⌊2x​⌋

Left son x < < 1 x << 1 x<<1

Right son x < < 1 ∣ 1 x << 1 | 1 x<<1∣1

Maximum range n < < 2 n << 2 n<<2

Five operations

• pushup
• pushdown
• build
• modify
• query

node structure

struct node{
    int l, r;
    ll sum, lazy;	// Sum of interval [l,r]
};

int n, m;
int w[MAXN];
node tr[MAXN << 2];

pushup

// Sum of parent nodes
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

pushdown

void pushdown(int u)	// Pass lazy flag down
{
    ll lazy = tr[u].lazy;
    if(lazy)
    {
        tr[u << 1].lazy += lazy;
        tr[u << 1 | 1].lazy += lazy;
        tr[u << 1].sum += (tr[u << 1].r - tr[u << 1].l + 1) * lazy;
        tr[u << 1 | 1].sum += (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1)*lazy;
        tr[u].lazy = 0; 	// The lazy flag of the parent node is reset to 0
    }
}

Build a tree

//build(1,1,n) establishes a segment tree from interval 1 to n
void build(int u, int l, int r)
{
    if(l == r)
    {
        tr[u] = {l,r,w[r]};
        return;
    }
    else
    {
        tr[u] = {l,r,0};
        int mid = (l+r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid+1, r);
        pushup(u);
    }
}

inquiry

// Sum interval [l,r]
// Call (1,l,r)
ll query(int u, int l, int r)
{
    if(l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
    else
    {
        pushdown(u);	// Drop lazy tag
        int mid = (tr[u].l + tr[u].r) >> 1;
        ll sum = 0;
        if(l <= mid) sum += query(u << 1, l, r);
        if(r > mid) sum += query(u << 1 | 1, l, r);
        return sum;
    }
}

Single point modification

// Call (1,x,v)
// a[x] += v
void modify(int u, int x, int v)
{
    if(tr[u].l == tr[u].r) tr[u].sum += v;
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1|1, x, v);
        pushup(u);
    }
}

Interval modification

// a[l]~a[r] += d
void change(int u, int l, int r, int d)	// Interval modification
{
    if(l <= tr[u].l && tr[u].r <= r) //If the parent node is completely overwritten, just mark the lazy flag. Don't worry about sending it down first, and then send it down when the sum needs to be used
    {
        tr[u].lazy += d;
        tr[u].sum += (tr[u].r - tr[u].l + 1) * d;
        return;
    }
    else
    {
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) change(u << 1, l, r, d);
        if(r > mid) change(u << 1 | 1, l, r, d);
        pushup(u);
    }
}

struct node{
    int l, r;
    ll sum, lazy;	// Sum of interval [l,r]
};

int n, m;
int w[MAXN];
node tr[MAXN << 2];

// Sum of parent nodes
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void pushdown(int u)	// Pass lazy flag down
{
    ll lazy = tr[u].lazy;
    if(lazy)
    {
        tr[u << 1].lazy += lazy;
        tr[u << 1 | 1].lazy += lazy;
        tr[u << 1].sum += (tr[u << 1].r - tr[u << 1].l + 1) * lazy;
        tr[u << 1 | 1].sum += (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1)*lazy;
        tr[u].lazy = 0; 	// The lazy flag of the parent node is reset to 0
    }
}

//build(1,1,n) establishes a segment tree from interval 1 to n
void build(int u, int l, int r)
{
    if(l == r)
    {
        tr[u] = {l,r,w[r]};
        return;
    }
    else
    {
        tr[u] = {l,r,0};
        int mid = (l+r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid+1, r);
        pushup(u);
    }
}

// Sum interval [l,r]
// Call (1,l,r)
ll query(int u, int l, int r)
{
    if(l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
    else
    {
        pushdown(u);	// Drop lazy tag
        int mid = (tr[u].l + tr[u].r) >> 1;
        ll sum = 0;
        if(l <= mid) sum += query(u << 1, l, r);
        if(r > mid) sum += query(u << 1 | 1, l, r);
        return sum;
    }
}

// Call (1,x,v)
// a[x] += v
void modify(int u, int x, int v)
{
    if(tr[u].l == tr[u].r) tr[u].sum += v;
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1|1, x, v);
        pushup(u);
    }
}

// a[l]~a[r] += d
void change(int u, int l, int r, int d)	// Interval modification
{
    if(l <= tr[u].l && tr[u].r <= r) //If the parent node is completely overwritten, just mark the lazy flag. Don't worry about sending it down first, and then send it down when the sum needs to be used
    {
        tr[u].lazy += d;
        tr[u].sum += (tr[u].r - tr[u].l + 1) * d;
        return;
    }
    else
    {
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) change(u << 1, l, r, d);
        if(r > mid) change(u << 1 | 1, l, r, d);
        pushup(u);
    }
}

3. Search and graph theory

Save map

Chain forward star

The data structure of this graph storage method is mainly an edge set array. As the name suggests, the edges of the graph are stored in an array.
Of course, to perfectly represent the graph structure, it is not enough to have an edge set array, but also an array to store the "pointer" to the first edge of each point.
Each edge needs to store the "pointer" of the next edge, so that it can easily traverse all edges of each point like an adjacency table.

#include <stdio.h>
#include <string.h>
// max vertex 
const int V = 100000;
// Maximum number of sides
const int E = 100000;
// Definition of edge structure
struct Edge {
    int to;         // Represents another vertex of this edge
    int next;       // Array subscript pointing to the next edge. A value of - 1 indicates that there is no next edge
};
// head[i] indicates the array subscript of the first edge of vertex 'I', - 1 indicates that vertex 'I' has no edge
int head[V];
Edge edge[E];
// For chain forward star initialization, you only need to initialize the vertex array
memset(head, -1, sizeof(head));
// How to add edges
// Add an edge a - > b, and the array subscript of this edge is ` id`
inline void addedge(int a, int b, int id)
{
    edge[id].to = b;
    edge[id].next = head[a];    // The new edge should be the first edge of vertex 'a', not the last edge
    head[a] = id++;
    return;
}
// Traverse all edges from the 'a' point
for (int i=head[a]; i!=-1; i=e[i].next) {
    // e[i] is the edge you are currently traversing, a - > e[i] to
}

search

DFS O ( m + n ) O(m+n) O(m+n)

int dfs(int u)
{
    vis[u] = true;
    for(int i = head[u];i != -1;i = edge[i].next)
    {
        int p = edge[i].to();
        if(vis[p]) continue;
        
        // Processing node
    }
}

dfs(1);

Center of gravity of tree

846. The center of gravity of the tree - AcWing question bank

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 50;
int head[MAXN];
bool vis[MAXN];
struct Edge{
    int to, next;
}edge[MAXN];
int n, id, ans;

inline void addedge(int a, int b)
{
    edge[id].to = b;
    edge[id].next = head[a];
    head[a] = id;
    id++;
}

// Number of nodes in subtree with u as root
int dfs(int u)
{
    int res = 0, sum = 1;
    vis[u] = true;
    for(int i = head[u];i != -1;i = edge[i].next)	// Traverse tree node
    {
        int p = edge[i].to;
        if(vis[p]) continue;
        int son = dfs(p);
        res = max(res, son);
        sum += son;
    }
    res = max(res,n-sum);	// The number of nodes of the subtree formed by the remaining points
    ans = min(ans,res);
    return sum;
}

int main()
{
    scanf("%d",&n);
    memset(vis,false,sizeof(vis));
    memset(head,-1,sizeof(head));
    for(int i = 1;i <= n-1;i++)
    {
        int a, b;
        scanf("%d%d",&a,&b);
        addedge(a,b);
        addedge(b,a);
    }
    ans = n;
    dfs(1);
    printf("%d\n",ans);
    return 0;
}

Width first search (BFS) O ( m + n ) O(m+n) O(m+n)

queue<int> q;
vis[1] = true; // Indicates that point 1 has been traversed
q.push(1);

while (q.size())
{
    int u = q.front();
    q.pop();

    for (int i = head[u]; i != -1; i = edge[i].next)
    {
        int p = edge[i].to;
        if(vis[p]) continue;
        vis[p] = true; // Indicates that point j has been traversed
        q.push(p);
    }
}

847. The level of the point in the figure - AcWing question bank

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e5+50;
const int inf = 0x3f3f3f3f;
int head[MAXN];
struct Edge{
    int to, next;
}edge[MAXN];
bool vis[MAXN];
int dist[MAXN];
int n, m, id;
queue<int>q;

inline void addedge(int a, int b)
{
    edge[id].to = b;
    edge[id].next = head[a];
    head[a] = id;
    id++;
    return;
}

int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++) dist[i] = inf;
    while(m--)
    {
        int a, b;
        scanf("%d%d",&a,&b);
        addedge(a,b);
    }
    q.push(1);
    vis[1] = true;
    dist[1] = 0;
    
    while(!q.empty())
    {
        int p = q.front();
        q.pop();
        
        for(int i = head[p];i != -1;i = edge[i].next)
        {
            int u = edge[i].to;
            if(vis[u]) continue;
            vis[u] = true;
            dist[u] = min(dist[u],dist[p]+1);
            q.push(u);
        }
    }
    
    if(dist[n] == inf) printf("-1\n");
    else printf("%d\n",dist[n]);
    
    return 0;
}

Topological sorting O ( m + n ) O(m+n) O(m+n)

848. Topological sequence of digraph - AcWing question bank

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<queue>
const int MAXN = 2e5+50;
using namespace std;
int n, m, id;
int head[MAXN];
struct Edge{
    int to, next;
}edge[MAXN];
bool vis[MAXN];
int ans[MAXN];
int d[MAXN]; // Storage penetration
queue<int>q;

inline void addedge(int a, int b)
{
    edge[id].to = b;
    edge[id].next = head[a];
    head[a] = id;
    id++;
    return;
}

bool topsort()
{
    int cnt = 0;
    for(int i = 1;i <= n;i++) {
        if(d[i] == 0) {
            q.push(i);
        }
    }
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        ans[cnt++] = u;

        for(int i = head[u];i != -1;i = edge[i].next)
        {
            int p = edge[i].to;
            d[p]--;
            if(d[p] == 0) q.push(p);
        }
    }
    if(cnt < n) return false;
    else return true;
}

int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    while(m--)
    {
        int a, b;
        scanf("%d%d",&a,&b);
        addedge(a,b);
        d[b]++;
    }

    bool flag = topsort();
    if(flag == true) {
        for(int i = 0;i < n;i++) printf("%d ",ans[i]);
    }

    else printf("-1\n");

    return 0;
}

Shortest path problem

• Floyd algorithm is a multi-source shortest path algorithm with the highest complexity( n 3 n^3 n3), usually used in problems where the starting point is not fixed with few points. It can solve the negative edge (negative weight) but not the negative ring.
• Dijkstra algorithm is a single source shortest path algorithm with the most common time complexity( n 2 n^2 n2) can be achieved after optimization( n l o g n nlogn nlogn), can not solve the negative edge problem, sparse graph (the range of points is large, but there are few edges, and the number of edges ∣ E ∣ |E| ∣ E ∣ much less than ∣ V ∣ ² |V|² ∣V∣ ²) It takes more space.
• SPFA algorithm is suitable for sparse graphs and can solve the problems with negative weighted edges and negative rings, but its efficiency is lower than Dijkstra in dense graphs.

Dijkstra

Naive Dijstra algorithm O ( n 2 + m ) O(n^2+m) O(n2+m)

Time complexity O ( n 2 + m ) O(n^2+m) O(n2+m)

int dijkstra()
{
    memset(dist,INF,sizeof(dist));
    dist[1] = 0;
    
    for(int i = 1;i <= n-1;i++)
    {
        int t = -1;
        for(int j = 1;j <= n;j++)
        {
            if(!vis[j] && (t == -1 || dist[j] < dist[t]))
            {
                t = j;
            }
        }
        vis[t] = true;
        for(int k = head[t];k != -1;k = edge[k].next)
        {
            int u = edge[k].to;
            if(vis[u]) continue;
            if(dist[u] > dist[t] + edge[k].w)
            {
                dist[u] = dist[t] + edge[k].w;
            }
        }
    }
    if(dist[n] == INF) return -1;
    else return dist[n];
}

849. Dijkstra finding the shortest path I - AcWing question bank

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;

const int MAXN = 1e5 + 50;
const int INF = 0x3f3f3f3f;

int head[MAXN], dist[MAXN];
bool vis[MAXN];

struct Edge{
  int to, next, w;
}edge[MAXN];

int n, m, id;

inline void addedge(int a, int b, int w)
{
    edge[id].to = b;
    edge[id].next = head[a];
    head[a] = id;
    edge[id].w = w;
    id++;
    return;
}

int dijkstra()
{
    memset(dist,INF,sizeof(dist));
    dist[1] = 0;
    
    for(int i = 1;i <= n-1;i++)	// A total of n-1 operations were performed
    {
        int t = -1;
        for(int j = 1;j <= n;j++)	// Find the minimum value
        {
            if(!vis[j] && (t == -1 || dist[j] < dist[t]))
            {
                t = j;
            }
        }
        vis[t] = true;
        for(int k = head[t];k != -1;k = edge[k].next)	// Traverse all edges starting at this vertex
        {
            int u = edge[k].to;
            if(vis[u]) continue;
            if(dist[u] > dist[t] + edge[k].w)
            {
                dist[u] = dist[t] + edge[k].w;
            }
        }
    }
    if(dist[n] == INF) return -1;
    else return dist[n];
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(head,-1,sizeof(head));
    while(m--)
    {
        int a, b, w;
        scanf("%d%d%d",&a,&b,&w);
        addedge(a,b,w);
    }
    int ans = dijkstra();
    printf("%d\n",ans);
}

Heap optimization algorithm O ( m l o g n ) O(mlogn) O(mlogn)

Time complexity O ( m l o g n ) O(mlogn) O(mlogn), n n n represents the number of points, m m m represents the number of sides

int dijkstra()
{
    for(int i = 1;i <= n;i++) dist[i] = 0x3f3f3f3f;
    dist[1] = 0;
    q.push({0,1});

    while(!q.empty())
    {
        auto u = q.top();
        q.pop();
        
        int dis = u.first;
        int idx = u.second;
        
        if(vis[idx]) continue;
        vis[idx] = true;
        
        for(int i = head[idx]; i != -1;i = edge[i].next)
        {
            int p = edge[i].to;
            if(dist[p] > dis + edge[i].w)
            {
                dist[p] = dis + edge[i].w;
                q.push({dist[p],p});	// Priority queue access minimum dist
            }
        }
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

850. Dijkstra finding the shortest path II - AcWing question bank

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

typedef pair<int,int> PII;
const int MAXN = 2e5+50;
int head[MAXN];
struct Edge{
    int to, next, w;
}edge[MAXN];
int dist[MAXN];
priority_queue<PII,vector<PII>,greater<PII>>q;
int n, m, id;
bool vis[MAXN];

inline void addedge(int a, int b, int w)
{
    edge[id].to = b;
    edge[id].next = head[a];
    edge[id].w = w;
    head[a] = id;
    id++;
    return;
}

int dijkstra()
{
    for(int i = 1;i <= n;i++) dist[i] = 0x3f3f3f3f;
    dist[1] = 0;
    q.push({0,1});

    while(!q.empty())
    {
        auto u = q.top();
        q.pop();
        
        int dis = u.first;
        int idx = u.second;
        
        if(vis[idx]) continue;
        vis[idx] = true;
        
        for(int i = head[idx]; i != -1;i = edge[i].next)
        {
            int p = edge[i].to;
            if(dist[p] > dis + edge[i].w)
            {
                dist[p] = dis + edge[i].w;
                q.push({dist[p],p});
            }
        }
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(head,-1,sizeof(head));
    while(m--)
    {
        int a, b, w;
        scanf("%d%d%d",&a,&b,&w);
        addedge(a,b,w);
    }
    int ans = dijkstra();
    printf("%d\n",ans);

    return 0;
}

Floyd O ( n 3 ) O(n^3) O(n3)

initialization:
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;

// After the algorithm, d[a][b] represents the shortest distance from a to B
void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

854. Floyd finding the shortest path - AcWing question bank

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<cstring>

const int INF = 1e9;
using namespace std;
int n, m, k;
int dist[205][205];

int main()
{
    scanf("%d%d%d",&n,&m,&k);
    
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            if(i == j) dist[i][j] = 0;
            else dist[i][j] = INF;
        }
    }
    
    while(m--)
    {
        int x, y, z;
        scanf("%d%d%d",&x,&y,&z);
        dist[x][y] = min(dist[x][y],z);
    }
    
    for(int k = 1;k <= n;k++)
    {
        for(int i = 1;i <= n;i++)
        {
            for(int j = 1;j <= n;j++)
            {
                dist[i][j] = min(dist[i][j],dist[i][k]+dist[k][j]);
            }
        }
    }
    
    while(k--)
    {
        int x, y;
        scanf("%d%d",&x,&y);
        if(dist[x][y] >= INF/2) printf("impossible\n");	// Because of the negative edge weight, it is reasonable to be greater than INF/2
        else printf("%d\n",dist[x][y]);
    }
    return 0;
}

Bellman_Ford algorithm

Naive algorithm O ( m n ) O(mn) O(mn)

Time complexity O ( m n ) O(mn) O(mn)

Limited number of edges k

bool bellman_ford()
{
    memset(dist,INF,sizeof(dist));
    dist[1] = 0;
    for(int i = 1;i <= k;i++)
    {
        memcpy(last,dist,sizeof(dist));	// The auxiliary array stores the results of the previous round to avoid multiple changes in a loop
        for(int j = 0;j < id;j++)	// Update by traversing all edges
        {
            int u = edge[j].from;
            int v = edge[j].to;
            if(dist[v] > last[u] + edge[j].w)
            {
                dist[v] = last[u] + edge[j].w;	// Slack operation
            }
        }
    }
    // After n operations, the triangular inequality dist [a] < = dist [b] + W is satisfied
    if(dist[n] >= INF /2) return false;
    else return true;
}

853. Shortest path with edge limit - AcWing question bank

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>

using namespace std;
const int MAXN = 10010;
const int INF = 0x3f3f3f3f;
int head[MAXN], dist[MAXN], last[MAXN];
struct Edge{
  int from, next, to, w;
}edge[MAXN];

int n, m, k, id;

inline void addedge(int a, int b, int w)
{
    edge[id].to = b;
    edge[id].from = a;
    edge[id].next = head[a];
    head[a] = id;
    edge[id].w = w;
    id++;
    return;
}

bool bellman_ford()
{
    memset(dist,INF,sizeof(dist));
    dist[1] = 0;
    for(int i = 1;i <= k;i++)
    {
        memcpy(last,dist,sizeof(dist));
        for(int j = 0;j < id;j++)
        {
            int u = edge[j].from;
            int v = edge[j].to;
            if(dist[v] > last[u] + edge[j].w)
            {
                dist[v] = last[u] + edge[j].w;
            }
        }
    }
    if(dist[n] >= INF /2) return false;
    else return true;
}

int main()
{
    scanf("%d%d%d",&n,&m,&k);
    memset(head,-1,sizeof(head));
    while(m--)
    {
        int a, b, w;
        scanf("%d%d%d",&a,&b,&w);
        addedge(a,b,w);
    }
    bool flag = bellman_ford();
    if(flag) printf("%d\n",dist[n]);
    else printf("impossible\n");
    return 0;
}

SPFA algorithm O ( m ) O(m) O(m)~ O ( m n ) O(mn) O(mn)

Condition: no negative ring

dist[b] = min(dist[b],dist[a]+w)

dist[b] becomes smaller only when dist[a] becomes smaller

SPFA is optimized based on this and uses a queue storage

int n;      // Total points
int h[N], w[N], e[N], ne[N], idx;       // The adjacency table stores all edges
int dist[N];        // Store the shortest distance from each point to point 1
bool st[N];     // Stores whether each point is in the queue

// Find the shortest distance from point 1 to point n. if you can't walk from point 1 to point n, return - 1
int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);
    st[1] = true;

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        st[t] = false;	// Out of line deletion

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])     // If j already exists in the queue, there is no need to insert j repeatedly
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

851. spfa finding the shortest path - AcWing question bank

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int MAXN = 1e5+50;
const int INF = 0x3f3f3f3f;

int head[MAXN], dist[MAXN];
bool vis[MAXN];
struct Edge{
    int to, next, w;
}edge[MAXN];
int n, m, id;
queue<int>q;

inline void addedge(int a, int b, int w)
{
    edge[id].to = b;
    edge[id].next = head[a];
    head[a] = id;
    edge[id].w = w;
    id++;
    return;
}

int spfa()
{
    memset(dist,INF,sizeof(dist));
    
    vis[1] = true;
    dist[1] = 0;
    q.push(1);
    
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        
        vis[u] = false;
        
        for(int i = head[u]; i != -1;i = edge[i].next)
        {
            int p = edge[i].to;
            if(dist[p] > dist[u] + edge[i].w)
            {
                dist[p] = dist[u] + edge[i].w;
                if(!vis[p])
                {
                    vis[p] = true;
                    q.push(p);
                }
            }
        }
    }
    
    if(dist[n] == INF) return -1;
    else return dist[n];
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(head,-1,sizeof(head));
    while(m--)
    {
        int x, y, z;
        scanf("%d%d%d",&x,&y,&z);
        addedge(x,y,z);
    }
    int ans = spfa();
    if(ans == -1) printf("impossible\n");
    else printf("%d\n",ans);
    return 0;
}

SPFA finding negative ring O ( m n ) O(mn) O(mn)

bool spfa()
{
    memset(cnt,0,sizeof(cnt));
    memset(dist,INF,sizeof(dist));
    
    dist[1] = 0;
    vis[1] = true;
    q.push(1);
    
    for(int i = 1;i <= n;i++) {
        vis[i] = true;
        q.push(i);
    }
    
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        
        vis[u] = false;
        
        for(int i = head[u];i != -1;i = edge[i].next)
        {
            int p = edge[i].to;
            
            if(dist[p] > dist[u] + edge[i].w)
            {
                dist[p] = dist[u] + edge[i].w;
                cnt[p] = cnt[u] + 1;
                if(cnt[p] >= n) return true;
                if(!vis[p])
                {
                    vis[p] = true;
                    q.push(p);
                }
            }
        }
    }
    return false;
}

852. spfa judgment negative loop - AcWing question bank

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>

using namespace std;
const int MAXN = 10010;
const int INF = 0x3f3f3f3f;
int head[MAXN], cnt[MAXN], dist[MAXN];
bool vis[MAXN];
struct Edge{
    int to, next, w;
}edge[MAXN];
queue<int>q;
int n, m, id;

inline void addedge(int a, int b, int w)
{
    edge[id].to = b;
    edge[id].next = head[a];
    head[a] = id;
    edge[id].w = w;
    id++;
    return;
}

bool spfa()
{
    memset(cnt,0,sizeof(cnt));
    memset(dist,INF,sizeof(dist));
    
    dist[1] = 0;
    vis[1] = true;
    q.push(1);
    
    for(int i = 1;i <= n;i++) {
        vis[i] = true;
        q.push(i);
    }
    
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        
        vis[u] = false;
        
        for(int i = head[u];i != -1;i = edge[i].next)
        {
            int p = edge[i].to;
            
            if(dist[p] > dist[u] + edge[i].w)
            {
                dist[p] = dist[u] + edge[i].w;
                cnt[p] = cnt[u] + 1;
                if(cnt[p] >= n) return true;
                if(!vis[p])
                {
                    vis[p] = true;
                    q.push(p);
                }
            }
        }
    }
    return false;
    
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(head,-1,sizeof(head));
    while(m--)
    {
        int x, y, z;
        scanf("%d%d%d",&x,&y,&z);
        addedge(x,y,z);
    }
    bool flag = spfa();
    if(flag) printf("Yes\n");
    else printf("No\n");
    return 0;
}

minimum spanning tree

Prim

Plain Prim O ( n 2 + m ) O(n^2+m) O(n2+m)

int n;      // n represents the number of points
int g[N][N];        // Adjacency matrix, storing all edges
int dist[N];        // Stores the distance from other points to the current minimum spanning tree
bool st[N];     // Stores whether each point is already in the spanning tree


// If the graph is not connected, inf (the value is 0x3f3f3f3f) is returned; otherwise, the sum of tree edge weights of the minimum spanning tree is returned
int prim()
{
    memset(dist, 0x3f, sizeof dist);

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        if (i && dist[t] == INF) return INF;

        if (i) res += dist[t];
        st[t] = true;

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
    }

    return res;
}

858. Prim algorithm for minimum spanning tree - AcWing question bank

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>

using namespace std;
const int MAXN = 1e5+50;
const int INF = 0x3f3f3f3f;
int dist[MAXN];
bool vis[MAXN];
int w[505][505];
int n, m;

int prim()
{
    int res = 0;
    memset(dist,INF,sizeof(dist));
    for(int i = 0;i < n;i++)
    {
        int t = -1;
        for(int j = 1;j <= n;j++)
        {
            if(!vis[j] && (t == -1 || dist[t] > dist[j]))
            {
                t = j;
            }
        }

        if(i && dist[t] == INF) return INF;

        if(i) res += dist[t];
        vis[t] = true;

        for(int j = 1;j <= n;j++) dist[j] = min(dist[j],w[t][j]);
    }
    return res;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            if(i == j) w[i][j] = 0;
            else w[i][j] = INF;
        }
    }
    while(m--)
    {
        int x, y, z;
        scanf("%d%d%d",&x,&y,&z);
        w[x][y] = w[y][x] = min(w[x][y],z);
    }
    int ans = prim();
    if(ans == INF) printf("impossible\n");
    else printf("%d\n",ans);
    return 0;
}

Kruskal O ( m l o g m ) O(mlogm) O(mlogm)

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 2e5+50;

struct Edge{
    int from, to, w;
    bool operator<(const Edge &a)
    {
        return w < a.w;
    }
}edge[MAXN];

int n, m;
int fa[MAXN];

int find(int x)
{
    if(x != fa[x]) fa[x] = find(fa[x]);
    return fa[x];
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 0;i < m;i++)
    {
        int x, y, w;
        scanf("%d%d%d",&x,&y,&w);
        edge[i].from = x;
        edge[i].to = y;
        edge[i].w = w;
    }
    
    int res = 0, cnt = 0;
    
    for(int i = 1;i <= n;i++) fa[i] = i;
    sort(edge,edge+m);
    
    for(int i = 0;i < m;i++)
    {
        int from = edge[i].from;
        int to = edge[i].to;
        int u = find(from), v = find(to);
        if(u != v) {
            cnt++;
            res += edge[i].w;
            fa[u] = v;
        }
    }
    
    if(cnt < n-1) printf("impossible\n");
    else printf("%d\n",res);
    
    return 0;
}

Bipartite graph

Color discrimination bipartite graph O ( m + n ) O(m+n) O(m+n)

int n;      // n represents the number of points
int h[N], e[M], ne[M], idx;     // Adjacency table storage graph
int color[N];       // Represents the color of each point, - 1 represents undyed, 0 represents white, and 1 represents black

// Parameters: u represents the current node and c represents the color of the current point
bool dfs(int u, int c)
{
    color[u] = c;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (color[j] == -1)
        {
            if (!dfs(j, !c)) return false;
        }
        else if (color[j] == c) return false;
    }

    return true;
}

bool check()
{
    memset(color, -1, sizeof color);
    bool flag = true;
    for (int i = 1; i <= n; i ++ )
        if (color[i] == -1)
            if (!dfs(i, 0))
            {
                flag = false;
                break;
            }
    return flag;
}

hungarian algorithm O ( m n ) O(mn) O(mn)

int n1, n2;     // n1 represents the number of points in the first set and n2 represents the number of points in the second set
int h[N], e[M], ne[M], idx;     // The adjacency table stores all edges. Only the edges from the first set to the second set will be used in the Hungarian algorithm, so only the edges in one direction are stored here
int match[N];       // Stores which point in the first set each point in the second set currently matches
bool st[N];     // Indicates whether each point in the second set has been traversed

bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }

    return false;
}

// Find the maximum number of matches, and enumerate whether each point in the first set can match the points in the second set
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
    memset(st, false, sizeof st);
    if (find(i)) res ++ ;
}

4. Mathematical knowledge

Divisor and factor

Determination of prime number by trial division

bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

Decomposition of prime factor by trial division O ( n 1 2 ) O(n^{\frac{1}{2}}) O(n21​)

void get_primes(int n)
{
    for(int i = 2;i <= n/i;i++)
    {
        int s = 0;
        while(n % i == 0)
        {
            n /= i;
            s++;
        }
        if(s) printf("%d %d\n",i,s);
    }
    if(n > 1) printf("%d 1\n",n);
    printf("\n");
}

Linear sieve for prime number

int primes[MAXN], cnt;     // Primes [] stores all primes
bool vis[MAXN];         // Is vis[x] storage x screened out

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!vis[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n ; j ++ )
        {
            vis[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

Try division to find divisor

void get_divisors(int n)
{
    for(int i = 1;i * i <= n;i++)
    {
        if(n % i == 0)
        {
            res.push_back(i);
            if(i * i != n) res.push_back(n/i);
        }
    }
    sort(res.begin(),res.end());
}

Sum of divisors and divisors

If N = p1^c1 * p2^c2 * ... *pk^ck
 Approximate number: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
Sum of divisors: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

greatest common divisor

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

Euler function

φ ( n ) \varphi(n) φ (n) Show 1 − N 1-N 1 − N and N N The number of N coprime numbers.

If in the fundamental theorem of arithmetic, N = p 1 α 1 p 2 α 2 ... p n α n N=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_n^{\alpha_n} N=p1α1​​p2α2​​...pnαn​​

be φ ( N ) = N ∗ p 1 − 1 p 1 ∗ p 2 − 1 p 2 ⋯ ∗ p n − 1 p n \varphi(N) = N * \frac {p_1-1}{p_1} * \frac {p_2-1}{p_2} \dots * \frac {p_n-1}{p_n} φ(N)=N∗p1​p1​−1​∗p2​p2​−1​⋯∗pn​pn​−1​

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;

int main()
{
    scanf("%d",&n);
    while(n--)
    {
        int x;
        scanf("%d",&x);
        int res = x;
        for(int i = 2;i * i <= x;i++)
        {
            if(x % i == 0) {
                res = res / i * (i-1);
                while(x % i == 0) x /= i;
            }
        }
        if(x > 1) res = res / x * (x-1);
        printf("%d\n",res);
    }
    return 0;
}

Principle of finding Euler function by linear sieve method

principle

The Euler function is independent of the number of prime numbers after decomposing the prime factor

therefore φ ( i ∗ p j ) \varphi(i*p_j) φ (i * pj) can be divided into two cases, p j p_j pj ， is a prime number

if i i i and p j p_j pj ＾ coprime

be φ ( i ∗ p j ) = ( i ∗ p j ) ∗ ( 1 − 1 p 1 ) ∗ ⋯ ∗ ( 1 − 1 p j ) ... ( 1 − 1 p k ) = φ ( i ) ∗ p j ∗ ( 1 − 1 p j ) = φ ( i ) ∗ ( p j − 1 ) \varphi(i*p_j) = (i*p_j)*(1-\frac{1}{p_1})* \dots * (1-\frac{1}{p_j}) \dots (1-\frac{1}{p_k}) = \varphi(i)*p_j*(1-\frac{1}{p_j}) = \varphi(i) * (p_j-1) φ(i∗pj​)=(i∗pj​)∗(1−p1​1​)∗⋯∗(1−pj​1​)...(1−pk​1​)=φ(i)∗pj​∗(1−pj​1​)=φ(i)∗(pj​−1)

if i i In i p j p_j pj ＾ this factor

be v a r p h i ( i ∗ p j ) = ( i ∗ p j ) ∗ ( 1 − 1 p 1 ) ∗ ⋯ ∗ ( 1 − 1 p j ) ... ( 1 − 1 p k ) = φ ( i ) ∗ p j varphi(i*p_j) = (i*p_j)*(1-\frac{1}{p_1})* \dots * (1-\frac{1}{p_j}) \dots (1-\frac{1}{p_k}) = \varphi(i)*p_j varphi(i∗pj​)=(i∗pj​)∗(1−p1​1​)∗⋯∗(1−pj​1​)...(1−pk​1​)=φ(i)∗pj​

void get_euler(int n)
{
    euler[1] = 1;

    for(int i = 2;i <= n;i++)
    {
        if(!vis[i])
        {
            prime[cnt++] = i;
            euler[i] = i-1;
        }

        for(int j = 0;prime[j] * i <= n;j++)
        {
            int t = i * prime[j];
            vis[t] = true;
            if(i % prime[j] == 0)
            {
                euler[t] = euler[i] * prime[j];
                break;
            }
            euler[t] = euler[i] * (prime[j]-1);
        }
    }
}

Euler theorem

if a a a and n n n coprime, then there is a φ ( n ) ≡ 1 ( m o d n ) a^{\varphi(n)} \equiv 1 (mod \quad n) aφ(n)≡1(modn)

prove:

In 1~n, a 1 , a 2 , ... , a φ ( n ) a_1,a_2,\dots, a_{\varphi(n)} a1​,a2​,…,a φ (n) Both and n n n coprime number

At the same time because a a a and n n n coprime, a a 1 , a a 2 , ... , a φ ( n ) aa_1,aa_2,\dots,a_{\varphi(n)} aa1​,aa2​,…,a φ (n) And n n n coprime

a a i ≡ a a j ≡ 1 m o d    n aa_i \equiv aa_j \equiv 1 \mod n aai​≡aaj​≡1modn

a ( a i − a j ) ≡ 0 m o d    n a(a_i-a_j) \equiv 0 \mod n a(ai​−aj​)≡0modn

a i ≡ a j m o d    n a_i \equiv a_j \mod n ai​≡aj​modn

therefore a 1 , a 2 , a 3 , ... a φ ( n ) a_1,a_2,a_3,\dots a_{\varphi(n)} a1​,a2​,a3​,…a φ (n) And a a 1 , a a 2 , a a 3 , ... , a φ ( n ) aa_1,aa_2,aa_3,\dots, a_{\varphi(n)} aa1​,aa2​,aa3​,…,a φ (n) Just m o d    n \mod n A rearrangement under modn

therefore a φ ( n ) ∗ a 1 ∗ a 2 ⋯ ∗ a v a r p h i ( n ) ≡ a 1 ∗ a 2 ⋯ ∗ a v a r p h i ( n ) m o d    n a^{\varphi(n)}*a_1*a_2\dots *a_{varphi(n)}\equiv a_1*a_2\dots *a_{varphi(n)} \mod n aφ(n)∗a1​∗a2​⋯∗avarphi(n)​≡a1​∗a2​⋯∗avarphi(n)​modn

therefore a φ ( n ) ≡ 1 ( m o d n ) a^{\varphi(n)} \equiv 1 (mod \quad n) aφ(n)≡1(modn)

Fast power and its application

Counting

int qmi(int a, int b, int p)
{
    int res = 1;
    while(b)
    {
        if(b & 1) res = (ll) res * a % p;
        b >>= 1;
        a = (ll) a * a % p;
    }
    return res;
}

Multiplicative inverse

a b = a ∗ b − 1 m o d    m \frac{a}{b} = a * b^{-1} \mod m ba​=a∗b−1modm

b − 1 b^{-1} b − 1 is the inverse element

Existence condition: b and m are coprime, that is, when m is a prime number, b has an inverse element

That is b ∗ x ≡ 1 m o d    n b*x \equiv 1 \mod n Solution of b * x ≡ 1modn x

According to Fermat's small theorem b n − 1 ≡ 1 m o d    n b^{n-1} \equiv 1 \mod n bn−1≡1modn

here b n − 2 b^{n-2} bn − 2 is b b A multiplicative inverse of b

extended euclidean algorithm

Pei Shu theorem

For any positive integer a, b. There must be integers x, y that satisfy a x + b y = g c d ( a , b ) ax+by = gcd(a,b) ax+by=gcd(a,b)

a x + b y = g c d ( a , b ) ax+by = gcd(a,b) ax+by=gcd(a,b)

When b = 0 b=0 When b=0, g c d ( a , b ) = a gcd(a,b)=a gcd(a,b)=a. x = 1 , y = 0 x=1,y=0 x=1,y=0 are a set of solutions satisfying the equation.

g c d ( a , b ) = g c d ( b , a   m o d   b ) gcd(a,b) = gcd(b,a\,mod\,b) gcd(a,b)=gcd(b,amodb). Substitute into the original formula and find b y + ( a − ⌊ a b ⌋ ∗ b ) ∗ x = g c d ( b , a   m o d   b ) by+(a-\lfloor \frac{a}{b} \rfloor*b)*x = gcd(b,a\,mod\,b) by+(a−⌊ba​⌋∗b)∗x=gcd(b,amodb)

therefore b y + a ∗ ( y − ⌊ a b ⌋ ∗ x ) = g c d ( b , a   m o d   b ) by+a*(y-\lfloor \frac{a}{b} \rfloor*x) = gcd(b,a\,mod\,b) by+a∗(y−⌊ba​⌋∗x)=gcd(b,amodb)

// Find x, y so that ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= (a/b) * x;
    return d;
}

Gauss elimination

// a[N][N] is an augmented matrix
int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )   // The row with the largest absolute value was found
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);      // Change the row with the largest absolute value to the top
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];      // Changes the first row of the current row to 1
        for (int i = r + 1; i < n; i ++ )       // Cancel all the following columns with the current row to 0
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; // unsolvable
        return 1; // There are infinite sets of solutions
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];

    return 0; // There is a unique solution
}

Combination number

Recursive combination number

// c[a][b] represents the number of schemes to select b from a apple
for (int i = 0; i < N; i ++ )
    for (int j = 0; j <= i; j ++ )
        if (!j) c[i][j] = 1;
        else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

Fast power combination number

//Firstly, the remainder fact[N] of all factorial modules and the inverse element infact[N] of all factorial modules are preprocessed
//If the modular number is a prime number, the inverse element can be solved by Fermat's small theorem
int qmi(int a, int b, int p) // Counting 
{
    int res = 1;
    while(b)
    {
        if(b & 1) res = (ll)res * a % p;
        b >>= 1;
        a = (ll)a * a % p;
    }
    return res;
}

void init()// Remainder of preprocessing factorial and remainder of factorial inverse
{
    fact[0] = infact[0] = 1;
    for(int i = 1;i <= 1e5+5;i++)
    {
        fact[i] = (ll)fact[i-1] * i % MOD;
        infact[i] = (ll)infact[i-1] * qmi(i,MOD-2,MOD) % MOD;
    }
}

Lucas theorem for combinatorial number

if p Is a prime number, then for any integer 1 <= m <= n，yes:
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)

int qmi(int a, int k, int p)  // Fast power template
{
    int res = 1 % p;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b, int p)  // Finding combinatorial number C(a, b) by theorem
{
    if (a < b) return 0;

    LL x = 1, y = 1;  // x is the numerator and y is the denominator
    for (int i = a, j = 1; j <= b; i --, j ++ )
    {
        x = (LL)x * i % p;
        y = (LL) y * j % p;
    }

    return x * (LL)qmi(y, p - 2, p) % p;
}

int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

Solving combinatorial number by decomposing prime factor method

When we need to find the true value of the combined number rather than the remainder of a number, the method of decomposing the prime factor is easier to use:
    1. Sieve method to find all prime numbers in the range
    2. adopt C(a, b) = a! / b! / (a - b)! This formula calculates the number of times of each quality factor. n! in p The number of times n / p + n / p^2 + n / p^3 + ...
    3. Multiply all prime factors with high-precision multiplication

int primes[N], cnt;     // Store all prime numbers
int sum[N];     // The number of times each prime number is stored
bool st[N];     // Has each number stored been screened out


void get_primes(int n)      // Finding prime number by linear sieve method
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)       // Please n! Number of times in
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)       // High precision by low precision template
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }

    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }

    return c;
}

get_primes(a);  // All prime numbers in the preprocessing range

for (int i = 0; i < cnt; i ++ )     // Find the number of times of each prime factor
{
    int p = primes[i];
    sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}

vector<int> res;
res.push_back(1);

for (int i = 0; i < cnt; i ++ )     // Multiply all prime factors with high-precision multiplication
    for (int j = 0; j < sum[i]; j ++ )
        res = mul(res, primes[i]);

Catalan number

given n 0 and n 1, they are arranged in some order, with a length of 2 n The number of sequences satisfying that the number of 0 in any prefix is not less than 1 is:
Cat(n) = C(2n, n) / (n + 1)

Inclusion exclusion principle (binary number represents set)

890. Divisible number - AcWing question bank

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

typedef long long ll;
const int MAXN = 20;
int n, m;
int primes[MAXN];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 0;i < m;i++) scanf("%d",&primes[i]);
    
    ll res = 0;
    
    for(int i = 1;i < 1 << m;i++)
    {
        int t = 1, cnt = 0;
        for(int j = 0;j < m;j++)
        {
            if(i >> j & 1)
            {
                cnt++;
                if((ll)t * primes[j] > n)
                {
                    t = -1;
                    break;
                }
                t *= primes[j];
            }
        }
        if(t != -1)
        {
            if(cnt % 2 == 1) res += n / t;
            else res -= n / t;
        }
    }
    
    printf("%d\n",res);
    
    return 0;
}

Game theory

NIM game

Given N stacks of items, the i stack of items has A i A_i Ai. Two players take turns. They can choose one pile at a time and take away any number of items. They can take away one pile, but they can't take it away. Whoever takes the last item wins. Both took the best strategy and asked whether the first hand would win.

We call this game NIM game. The state faced in the process of the game is called situation. The first action in the whole game is called the first hand, and the second action is called the second hand. If in a situation, no matter what action is taken, the game will be lost, it is said that the situation will be lost.
The so-called taking the optimal strategy means that if there is an action in a certain situation, which makes the opposite face face a doomed situation after the action, the action will be taken first. At the same time, such a situation is called victory. The game problems we discuss generally only consider the ideal situation, that is, the result of the game when both of them have no mistakes and take the optimal strategy action.
There is no draw in NIM game. There are only two situations: the first hand must win and the first hand must lose.

Theorem: the first player in NIM game must win if and only if A 1 A_1 A1​ ^$ A_2$ ^ ... ^ A n A_n An​ ≠ \ne ​= 0

Fair combination game ICG

If a game meets:

• Two players act alternately;
• At any time in the game process, the legal actions that can be performed have nothing to do with which player's turn;
• Players who cannot act will be judged negative;
• The game is called a fair combination game.
• NIM game belongs to fair combination game, but urban construction chess games, such as go, are not fair combination games. Because the two belligerents of go can only drop sunspots and whites respectively, the judgment of victory and defeat is also more complex, which does not meet conditions 2 and 3.

Directed graph game

Given a directed acyclic graph, the graph has a unique starting point on which a chess piece is placed. Two players alternately move the piece along the directed edge. They can move one step at a time. If they can't move, they will be judged negative. The game is called directed graph game.
Any fair combination game can be transformed into a directed graph game. The specific method is to regard each situation as a node in the graph, and there are directional edges from each bureau to the next situation that can be reached along the legal action.

Mex operation

Let S represent a set of nonnegative integers. mex(S) is defined as the operation to find the minimum nonnegative integer that does not belong to the set S, that is:
mex(S) = min{x}, x is a natural number, and X does not belong to S

SG function

In the directed graph game, for each node x, let there be k directed edges starting from X and reaching nodes y1, y2,..., yk respectively, define SG(x) as the set composed of the SG function values of the successor nodes y1, y2,..., yk of X, and then execute the result of mex(S) operation, that is:
SG(x) = mex({SG(y1), SG(y2), ..., SG(yk)})
In particular, the SG function value of the whole directed graph game G is defined as the SG function value of the starting point s of the directed graph game, that is, SG(G) = SG(s).

Sum of directed graph games

Let G1, G2,..., Gm be m digraph games. A directed graph game G is defined. Its action rule is to select any directed graph game Gi and take one step on Gi. G is called the sum of directed graph games G1, G2,..., Gm.
The SG function value of the sum of the digraph game is equal to the XOR sum of the SG function values of each sub game it contains, that is:
SG(G) = SG(G1) ^ SG(G2) ^ ... ^ SG(Gm)

theorem

A situation in a digraph game is certain to win if and only if the SG function value of the corresponding node is greater than 0.
A situation in a digraph game must fail if and only if the SG function value of the corresponding node is equal to 0.

893. Collection - Nim game - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<unordered_set>

using namespace std;

const int N = 110, M = 11010;
int s[N], f[M];
int n, k;

int sg(int x)
{
    if(f[x] != -1) return f[x];
    
    unordered_set<int> S;
    for(int i = 0;i < k;i++)
    {
        if(x >= s[i]) S.insert(sg(x-s[i]));
    }
    for(int i = 0;;i++)
    {
        if(S.count(i) == 0) {
            f[x] = i;
            return f[x];
        }
    }
}

int main()
{
    memset(f,-1,sizeof(f));
    scanf("%d",&k);
    for(int i = 0;i < k;i++) scanf("%d",&s[i]);
    scanf("%d",&n);
    int res = 0;
    for(int i = 0;i < n;i++)
    {
        int x;
        scanf("%d",&x);
        res ^= sg(x);
    }
    if(res) puts("Yes");
    else puts("No");
    return 0;
}

5. Dynamic planning

knapsack problem

0-1 Backpack

because f [ i ] f[i] f[i] only used f [ i − 1 ] f[i-1] f[i − 1], and the capacity of the second backpack does not exceed j j j. It can change from two dimensions to one dimension.

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;
int N, V;
const int MAXN = 1010;
int v[MAXN], w[MAXN], dp[MAXN];

int main()
{
    scanf("%d%d",&N,&V);
    for(int i = 1;i <= N;i++) scanf("%d%d",&v[i],&w[i]);
    for(int i = 1;i <= N;i++)
    {
        for(int j = V;j >= v[i];j--)
        {
            dp[j] = max(dp[j],dp[j-v[i]]+w[i]);
        }
    }
    int ans = dp[V];
    printf("%d\n",ans);
    return 0;
}

Complete Backpack

The above time complexity is O ( n 3 ) O(n^3) O(n3), which can be optimized as O ( n 2 ) O(n^2) O(n2)

#include<algorithm>
#include<iostream>
#include<cstdio>

using namespace std;
const int MAXN = 1010;

int v[MAXN], w[MAXN], dp[MAXN];
int N, V;

int main()
{
    scanf("%d%d",&N,&V);
    for(int i = 1;i <= N;i++) scanf("%d%d",&v[i],&w[i]);
    
    for(int i = 1;i <= N;i++)
    {
        for(int j = v[i];j <= V;j++)
        {
            dp[j] = max(dp[j],dp[j-v[i]]+w[i]);
        }
    }
    
    printf("%d\n",dp[V]);
    
    return 0;
}

Multiple Backpack

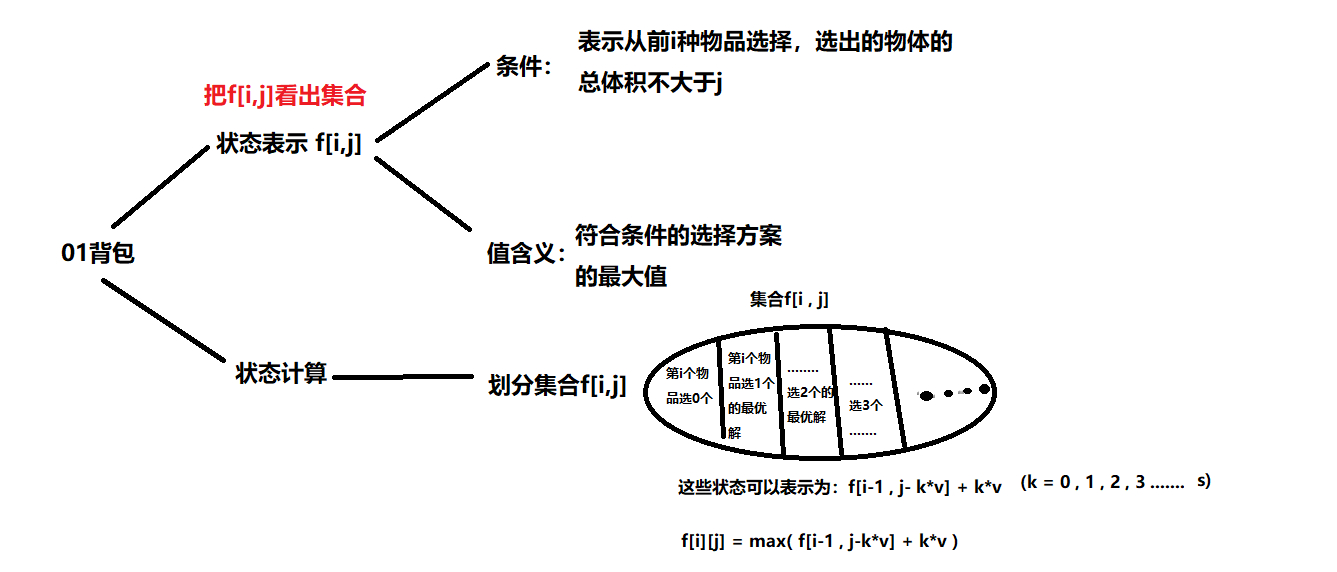
f[i][j] = max(f[i-1][j],f[i-1][j-k*v[i]]+k*w[i])       k = 0, 1, 2, .........,s[i]

Binary optimization method is adopted O ( N V log ⁡ S ) O(NV \log S) O(NVlogS)

#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;
const int MAXN = 25000, M = 2010;
int N, V, cnt;
int v[MAXN], w[MAXN], dp[M];

int main()
{
    scanf("%d%d",&N,&V);
    for(int i = 1;i <= N;i++)
    {
        int a, b, num;
        scanf("%d%d%d",&a,&b,&num);
        int k = 1;
        while(k <= num)
        {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            num -= k;
            k *= 2;
        }
        if(num > 0)
        {
            cnt++;
            v[cnt] = a * num;
            w[cnt] = b * num;
        }
    }
    
    for(int i = 1;i <= cnt;i++)
    {
        for(int j = V;j >= v[i];j--)
        {
            dp[j] = max(dp[j],dp[j-v[i]]+w[i]);
        }
    }
    
    printf("%d\n",dp[V]);
    
    return 0;
}

Group Backpack

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 110;
int N, V;
int s[MAXN], w[MAXN][MAXN], v[MAXN][MAXN], dp[MAXN][MAXN];

int main()
{
    scanf("%d%d",&N,&V);
    for(int i = 1;i <= N;i++)
    {
        scanf("%d",&s[i]);
        for(int j = 1;j <= s[i];j++)
        {
            scanf("%d%d",&v[i][j],&w[i][j]);
        }
    }
    
    for(int i = 1;i <= N;i++)
    {
        for(int j = 0;j <= V;j++)
        {
            dp[i][j] = dp[i-1][j];
            for(int k = 1;k <= s[i];k++)
            {
                if(j >= v[i][k]) dp[i][j] = max(dp[i][j], dp[i-1][j-v[i][k]]+w[i][k]);
            }
        }
    }
    
    printf("%d\n",dp[N][V]);
    return 0;
}

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;
const int MAXN = 110;
int N, V;
int v[MAXN][MAXN], w[MAXN][MAXN], s[MAXN], dp[MAXN];


int main()
{
    scanf("%d%d",&N,&V);
    for(int i = 1;i <= N;i++)
    {
        scanf("%d",&s[i]);
        for(int j = 1;j <= s[i];j++)
        {
            scanf("%d%d",&v[i][j],&w[i][j]);
        }
    }
    
    for(int i = 1;i <= N;i++)
    {
        for(int j = V;j >= 0;j--)
        {
            for(int k = 1; k <= s[i];k++)
            {
                if(j >= v[i][k]) dp[j] = max(dp[j],dp[j-v[i][k]]+w[i][k]);
            }
        }
    }
    
    printf("%d\n",dp[V]);
    
    return 0;
}

Linear DP

898. Digital triangle - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 510;
int a[MAXN][MAXN], dp[MAXN][MAXN];
int n;

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= i;j++)
        {
            scanf("%d",&a[i][j]);
        }
    }
    dp[1][1] = a[1][1];
    for(int i = 2;i <= n;i++)
    {
        for(int j = 1;j <= i;j++)
        {
            if(j == 1) dp[i][j] = dp[i-1][j] + a[i][j];
            else if(j == i) dp[i][j] = dp[i-1][j-1] + a[i][j];
            else dp[i][j] = max(dp[i-1][j],dp[i-1][j-1])+a[i][j];
        }
    }
    int ans = dp[n][1];
    for(int i = 1;i <= n;i++) ans = max(ans,dp[n][i]);
    printf("%d\n",ans);
    return 0;
}

895. Longest ascending subsequence - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

const int MAXN = 1010;
int n;
int a[MAXN], dp[MAXN];

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    for(int i = 1;i <= n;i++)
    {
        dp[i] = 1;
        for(int j = 1;j < i;j++)
        {
            if(a[i] > a[j]) dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    int ans = dp[n];
    for(int i = 1;i <= n;i++) ans = max(ans,dp[i]);
    printf("%d\n",ans);
    return 0;
}

O ( log ⁡ n ) O(\log n) O(logn) optimization

896. Longest ascending subsequence II - AcWing question bank

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;
const int MAXN = 1e5+50;
int a[MAXN], b[MAXN], n, id;

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)
    {
        scanf("%d",&a[i]);
    }
    b[id++] = a[1];
    for(int i = 2;i <= n;i++)	// Traverse each number
    {
        if(a[i] <= b[id-1])
        {
            int pos = lower_bound(b,b+id,a[i])-b;	// Binary find the first number greater than or equal to it and replace it
            b[pos] = a[i];
        }
        else b[id++] = a[i];
    }
    printf("%d\n",id);
    return 0;
}

897. Longest common subsequence - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

int n, m;
const int MAXN = 1005;
int dp[MAXN][MAXN];

int main()
{
    scanf("%d%d",&n,&m);
    char s[MAXN], t[MAXN];
    cin >> s+1 >> t+1;
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= m;j++)
        {
            if(s[i] == t[j]) dp[i][j] = dp[i-1][j-1]+1;
            else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
        }
    }
    int ans = dp[n][m];
    printf("%d\n",ans);
    return 0;
}

902. Shortest editing distance - AcWing question bank

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 1005;
int dp[MAXN][MAXN];
char s[MAXN], t[MAXN];
int n, m;

int min_3(int a, int b, int c)
{
    int tmp = min(a, b);
    return min(c,tmp);
}

int main()
{
    scanf("%d",&n);
    cin >> s+1;
    scanf("%d",&m);
    cin >> t+1;
    
    // Note initialization
    for(int i = 1;i <= n;i++) dp[i][0] = i;
    for(int j = 1;j <= m;j++) dp[0][j] = j;
    
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= m;j++)
        {
            if(s[i] == t[j]) dp[i][j] = dp[i-1][j-1];
            else dp[i][j] = min_3(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
        }
    }
    int ans = dp[n][m];
    printf("%d\n",ans);
    return 0;
}

Interval DP

282. Stone merging - AcWing question bank

Ensure that the number used in each interval is calculated before. So first enumerate the interval length.

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;
const int MAXN = 1010;

int dp[MAXN][MAXN], a[MAXN], sum[MAXN];
int n;

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) {
        scanf("%d",&a[i]);
        sum[i] = sum[i-1]+a[i];
    }
    for(int i = 1;i <= n;i++) dp[i][i] = 0;
    
    for(int len = 2;len <= n;len++)
    {
        for(int i = 1;i + len - 1 <= n;i++)
        {
            int l = i, r = i+len-1;
            dp[l][r] = dp[l][l]+dp[l+1][r]+sum[r]-sum[l-1];
            for(int k = l;k < r;k++)
            {
                dp[l][r] = min(dp[l][r],dp[l][k]+dp[k+1][r]+sum[r]-sum[l-1]);
            }
        }
    }
    int ans = dp[1][n];
    printf("%d\n",ans);
    return 0;
}

Count DP

900. Integer division - AcWing question bank

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;
const int MOD = 1e9+7;
const int MAXN = 1005;
int n;
ll dp[MAXN][MAXN];

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) dp[n][1] = 1;
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            if(j == i) dp[i][j] = (1 + dp[i][j-1]) % MOD;
            else if(i < j) dp[i][j] = dp[i][i];
            else dp[i][j] = (dp[i-j][j] + dp[i][j-1]) % MOD;
        }
    }
    printf("%d\n",dp[n][n]);
    return 0;
}

Digital DP

Case by case discussion

[a,b] 0~9 Number of occurrences
count(n,x) express[1,n]in x Number of occurrences
count(b,x)-count(a-1,x)
// Case by case discussion

Pressure DP

291. Mondrian's dream - AcWing question bank

When all the horizontal squares are finished, there is only one pendulum method for the vertical squares.

Therefore, all the placement methods are the same as the horizontal placement of small squares.

f[i][j] indicates whether column I has a small horizontal grid protruding from the previous column.

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;
typedef long long ll;
ll dp[12][3000];
bool vis[3000];

int main()
{
    while(true)
    {
        int n, m;
        scanf("%d%d",&n,&m);
        if(n == 0 && m == 0) break;
        memset(dp,0,sizeof(dp));
        for(int i = 0;i < 1 << n;i++)
        {
            vis[i] = true;
            int cnt = 0;
            for(int j = 0;j < n;j++)
            {
                if((i >> j) & 1)	// Pay attention to the operation order
                {
                    if(cnt % 2 == 1) vis[i] = false;
                }
                else cnt++;
            }
            if(cnt % 2 == 1) vis[i] = false;
        }
        dp[0][0] = 1;
        for(int i = 1;i <= m;i++)
        {
            for(int j = 0;j < (1<<n);j++)
            {
                for(int k = 0;k < (1<<n);k++)
                {
                    int s = j | k;
                    if(vis[s] && (j & k) == 0) dp[i][j] += dp[i-1][k];
                }
            }
        }
        ll ans = dp[m][0];
        printf("%lld\n",ans);
    }
    
    
    return 0;
}

91. Shortest Hamilton path - AcWing question bank

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>

using namespace std;

const int MAXN = 1 << 20;
const int INF = 0x3f3f3f3f;
int w[21][21], dp[MAXN][21];
int n;

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < n;j++)
        {
            scanf("%d",&w[i][j]);
        }
    }
    
    memset(dp,INF,sizeof(dp));
    
    dp[1][0] = 0;
    
    for(int i = 0;i < (1<<n);i++)
    {
        for(int j = 0;j < n;j++)
        {
            if((i >> j) & 1)
            {
                for(int k = 0;k < n;k++)
                {
                    if((i >> k) & 1)
                    dp[i][j] = min(dp[i][j],dp[i-(1 << j)][k] + w[k][j]);
                }
            }
        }
    }
    
    int ans = dp[(1 << n) - 1][n-1];
    printf("%d\n",ans);
    
    return 0;
}

Tree DP

// The subtree of u is s1,s2
f[u,0] = f[u,0] + max(f[s1,0],f[s1,1]) + max(f[s2,0],f[s2,1])
f[u,1] = f[u,1] + f[s1,0] + f[s2,0]

285. Dance without boss - AcWing question bank

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;
const int MAXN = 6010;
int n, id, head[MAXN], dp[MAXN][2], happy[MAXN];
struct Edge{
    int to, next;
}edge[MAXN];
bool has_father[MAXN];

void addedge(int a, int b)
{
    edge[id].to = b;
    edge[id].next = head[a];
    head[a] = id++;
    return;
}

void dfs(int u)
{
    dp[u][1] = happy[u];
    
    for(int i = head[u];i != -1;i = edge[i].next)
    {
        int p = edge[i].to;
        dfs(p);
        
        dp[u][1] += dp[p][0];
        dp[u][0] += max(dp[p][0],dp[p][1]);
    }
}

int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) scanf("%d",&happy[i]);
    
    for(int i = 1;i <= n-1;i++)
    {
        int a, b;
        scanf("%d%d",&a,&b);
        addedge(b,a);
        has_father[a] = true;
    }
    
    int root = 1;
    while(has_father[root])
    {
        root++;
    }
    dfs(root);
    int ans = max(dp[root][0],dp[root][1]);
    printf("%d\n",ans);
    
    return 0;
}

Memory search

901. Skiing - AcWing question bank

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;
const int MAXN = 305;
int n, m;
int dp[MAXN][MAXN], w[MAXN][MAXN];
int dx[4] = {0,1,0,-1}, dy[4] = {1,0,-1,0};

int dfs(int x, int y)
{
    if(dp[x][y] != -1) return dp[x][y];
    dp[x][y] = 1;
    for(int i = 0;i < 4;i++)
    {
        int u = x + dx[i], v = y + dy[i];
        if(u >= 1 && u <= n && v >= 1 && v <= m && w[u][v] < w[x][y])
        {
            dp[x][y] = max(dp[x][y],1+dfs(u,v));
        }
    }
    return dp[x][y];
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= m;j++)
        {
            scanf("%d",&w[i][j]);
        }
    }
    int ans = 1;
    memset(dp,-1,sizeof(dp));
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= m;j++)
        {
            ans = max(ans,dfs(i,j));
        }
    }
    printf("%d\n",ans);
    return 0;
}

6. Greed

Interval problem

905. Interval point selection - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

const int MAXN = 1e5+50;
int n;
struct node{	// Sort by right endpoint
    int l, r;
    bool operator<(const node &a)
    {
        if(r == a.r) return l < a.l;
        return r < a.r;
    }
}Node[MAXN];

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)
    {
        scanf("%d%d",&Node[i].l,&Node[i].r);
    }
    sort(Node+1,Node+n+1);
    int cnt = 0;
    int r;
    for(int i = 1;i <= n;i++)
    {
        if(!cnt || Node[i].l > r) {
            r = Node[i].r;
            cnt++;
        }
    }
    printf("%d\n",cnt);
    return 0;
}

908. Maximum number of disjoint intervals - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

const int MAXN = 1e5+50;
// Sort by right endpoint
struct node{
    int l, r;
    bool operator<(const node &a)
    {
        if(r == a.r) return l < a.l;
        return r < a.r;
    }
}Node[MAXN];
int n;

int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) scanf("%d%d",&Node[i].l,&Node[i].r);
    sort(Node+1,Node+1+n);
    int cnt = 0, r;
    for(int i = 1;i <= n;i++)
    {
        if(!cnt || Node[i].l > r)
        {
            r = Node[i].r;
            cnt++;
        }
    }
    printf("%d\n",cnt);
    return 0;
}

906. Interval grouping - AcWing question bank

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>

using namespace std;

const int MAXN = 1e5+50;
struct node{
    int l, r;
    bool operator<(const node &a)
    {
        if(l == a.l) return r < a.r;
        return l < a.l;
    }
}Node[MAXN];
int n;

priority_queue<int,vector<int>,greater<int>>pq;

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++)
    {
        scanf("%d%d",&Node[i].l,&Node[i].r);
    }
    sort(Node,Node+n);
    int cnt = 0;
    for(int i = 0;i < n;i++)
    {
        if(!cnt || pq.top() >= Node[i].l)
        {
            cnt++;
            pq.push(Node[i].r);
        }
        else {
            pq.pop();
            pq.push(Node[i].r);
        }
    }
    printf("%d\n",cnt);
    return 0;
}

Sort all start times and end times, add 1 to the required classrooms when meeting the start time, and reduce 1 to the required classrooms when meeting the end time. In the process of changing the number of classrooms required, the peak is the number of activities carried out at the same time, which is also the number of classrooms we need at least.

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
const int MAXN = 1e5+10;
int n;
int b[2*MAXN], idx;

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++)
    {
        int l, r;
        scanf("%d%d",&l,&r);
        b[idx++] = 2*l;	// Perform appropriate parity transformation
        b[idx++] = 2*r+1;	// Even numbers are added to avoid repetition
    }
    sort(b,b+idx);
    int t = 0, ans = 0;
    for(int i = 0;i < idx;i++)
    {
        if(b[i] % 2 == 0) t++;
        else t--;
        ans = max(ans,t);
    }
    printf("%d\n",ans);
    
    return 0;
}

AcWing 907. Interval coverage - acwing

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-iskx8axw-1629167397792) (C: / users / Dell / appdata / roaming / typora / typora user images / image-20210706105409443. PNG)]

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;

const int MAXN = 1e5+50;
struct node{
    int l, r;
    bool operator<(const node &a)	// Sort by left endpoint
    {
        return l < a.l;
    }
}Node[MAXN];
int n, le, ri;

int main()
{
    bool flag = true;
    scanf("%d%d",&le,&ri);
    scanf("%d",&n);
    for(int i = 0;i < n;i++) scanf("%d%d",&Node[i].l,&Node[i].r);
    sort(Node,Node+n);
    int start = le, tmp = le, cnt = 0;
    for(int i = 0;i < n;)
    {
        if(start >= ri) break;	// Exit beyond interval
        while(Node[i].l <= start && i < n)
        {
            tmp = max(tmp,Node[i].r);	// Fix the left endpoint and find the largest right endpoint
            i++;
        }
        cnt++;
        if(tmp == start) {
            flag = false;
            break;
        }
        start = tmp;
    }
    if(start < ri) flag = false;	// The interval length not found is recorded as false
    if(flag) printf("%d\n",cnt);
    else printf("-1\n");
    return 0;
}

Huffman tree

148. Combined fruit - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>

using namespace std;
const int MAXN = 10010;
int n;
int a[MAXN];
priority_queue<int,vector<int>,greater<int>>pq;

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++) {
        int x;
        scanf("%d",&x);
        pq.push(x);
    }
    int ans = 0;
    for(int i = 0;i < n-1;i++)
    {
        int u = pq.top();
        pq.pop();
        int v = pq.top();
        pq.pop();
        ans += u+v;
        pq.push(u+v);
    }
    printf("%d\n",ans);
    return 0;
}

sequence inequality

Activity - AcWing

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int n;
const int MAXN = 100010;
int a[MAXN];
int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++) scanf("%d",&a[i]);
    sort(a,a+n);	// Draw water according to the short one
    ll ans = 0, sum = 0;
    for(int i = 0;i < n;i++)
    {
        ans += sum;
        sum += a[i];
    }
    printf("%lld\n",ans);
}

Absolute value inequality

104. Warehouse location - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int MAXN = 100010;
int a[MAXN];
int n;
int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) {
        scanf("%d",&a[i]);
    }
    sort(a+1,a+n+1);
    int mid = a[n/2+1];	// Take the middle number as the site
    ll ans = 0;
    for(int i = 1;i <= n;i++) ans += abs(mid-a[i]);
    printf("%d\n",ans);
    return 0;
}

Push formula

So what we are asking for is to find out a kind of arrangement of cattle, so that m a x ( w 1 + ⋅ ⋅ ⋅ + w i − 1 − s i ) max(w_1+⋅⋅⋅+w_{i−1}−s_i) max(w1 + ⋅⋅⋅ + wi − 1 − si) is the smallest, and record this value as val.

In order to find the sorting scheme, you can exchange the positions of i, i+1 cattle to see what equivalent conditions are satisfied, so that the val after exchange is not larger than before.

Because s and W are positive numbers, w i − s i + 1 > − s i + 1 w_i−s_{i+1}>−s_{i+1} wi​−si+1​>−si+1​ , w i + 1 − s i > − s i w_{i+1}−s_i>−s_i wi+1​−si​>−si​
compare w i − s i + 1 w_i−s_{i+1} wi − si+1 − and w i + 1 − s i w_{i+1}−s_{i} wi+1 − si +

So we get the method: sort by w + s of each cow, and exchange when there is reverse order (i.e. ascending order),
Then calculate the dangerous value of each cow according to the meaning of the question, and record the maximum value

125. Acrobatic cow - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;
typedef long long ll;
int n;
const int MAXN = 50050;
ll sum, ans;
struct Cow{
    int s, w;
    bool operator<(const Cow &a)
    {
        return s+w < a.s+a.w;
    }
}cow[MAXN];

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++)
    {
        scanf("%d%d",&cow[i].w,&cow[i].s);
    }
    sort(cow,cow+n);
    ans -= cow[0].s;
    sum = cow[0].w;
    for(int i = 1;i < n;i++)
    {
        if(sum - cow[i].s > ans) ans = sum - cow[i].s;
        sum += cow[i].w;
    }
    printf("%lld\n",ans);
    return 0;
}

7. Spatiotemporal complexity analysis

Generally, the time limit of ACM or written test questions is 1 second or 2 seconds.
In this case, the number of operations in C + + code is controlled to 1 0 7 ∼ 1 0 8 10^7∼10^8 107 ∼ 108 is the best.

The time complexity of the code and how to select the algorithm under different data ranges are given below:

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-y0yz0fnm-1629167397793) (C: / users / Dell / appdata / roaming / typora / typora user images / image-20210706175918298. PNG)]

ode[i].l,&Node[i].r);
}
sort(Node,Node+n);
int cnt = 0;
for(int i = 0;i < n;i++)
{
if(!cnt || pq.top() >= Node[i].l)
{
cnt++;
pq.push(Node[i].r);
}
else {
pq.pop();
pq.push(Node[i].r);
}
}
printf("%d\n",cnt);
return 0;
}

Sort all start times and end times, add 1 to the required classroom when meeting the start time, and subtract 1 to the required classroom when meeting the end time,In the process of a series of changes in the number of classrooms needed, the peak is the number of simultaneous activities, which is also the number of classrooms we need at least.



```c++
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
const int MAXN = 1e5+10;
int n;
int b[2*MAXN], idx;

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++)
    {
        int l, r;
        scanf("%d%d",&l,&r);
        b[idx++] = 2*l;	// Perform appropriate parity transformation
        b[idx++] = 2*r+1;	// Even numbers are added to avoid repetition
    }
    sort(b,b+idx);
    int t = 0, ans = 0;
    for(int i = 0;i < idx;i++)
    {
        if(b[i] % 2 == 0) t++;
        else t--;
        ans = max(ans,t);
    }
    printf("%d\n",ans);
    
    return 0;
}

AcWing 907. Interval coverage - acwing

[external chain picture transferring... (IMG iskx8axw-1629167397792)]

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;

const int MAXN = 1e5+50;
struct node{
    int l, r;
    bool operator<(const node &a)	// Sort by left endpoint
    {
        return l < a.l;
    }
}Node[MAXN];
int n, le, ri;

int main()
{
    bool flag = true;
    scanf("%d%d",&le,&ri);
    scanf("%d",&n);
    for(int i = 0;i < n;i++) scanf("%d%d",&Node[i].l,&Node[i].r);
    sort(Node,Node+n);
    int start = le, tmp = le, cnt = 0;
    for(int i = 0;i < n;)
    {
        if(start >= ri) break;	// Exit beyond interval
        while(Node[i].l <= start && i < n)
        {
            tmp = max(tmp,Node[i].r);	// Fix the left endpoint and find the largest right endpoint
            i++;
        }
        cnt++;
        if(tmp == start) {
            flag = false;
            break;
        }
        start = tmp;
    }
    if(start < ri) flag = false;	// The interval length not found is recorded as false
    if(flag) printf("%d\n",cnt);
    else printf("-1\n");
    return 0;
}

Huffman tree

148. Combined fruit - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>

using namespace std;
const int MAXN = 10010;
int n;
int a[MAXN];
priority_queue<int,vector<int>,greater<int>>pq;

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++) {
        int x;
        scanf("%d",&x);
        pq.push(x);
    }
    int ans = 0;
    for(int i = 0;i < n-1;i++)
    {
        int u = pq.top();
        pq.pop();
        int v = pq.top();
        pq.pop();
        ans += u+v;
        pq.push(u+v);
    }
    printf("%d\n",ans);
    return 0;
}

sequence inequality

Activity - AcWing

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int n;
const int MAXN = 100010;
int a[MAXN];
int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++) scanf("%d",&a[i]);
    sort(a,a+n);	// Draw water according to the short one
    ll ans = 0, sum = 0;
    for(int i = 0;i < n;i++)
    {
        ans += sum;
        sum += a[i];
    }
    printf("%lld\n",ans);
}

Absolute value inequality

104. Warehouse location - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int MAXN = 100010;
int a[MAXN];
int n;
int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++) {
        scanf("%d",&a[i]);
    }
    sort(a+1,a+n+1);
    int mid = a[n/2+1];	// Take the middle number as the site
    ll ans = 0;
    for(int i = 1;i <= n;i++) ans += abs(mid-a[i]);
    printf("%d\n",ans);
    return 0;
}

Push formula

So what we are asking for is to find out a kind of arrangement of cattle, so that m a x ( w 1 + ⋅ ⋅ ⋅ + w i − 1 − s i ) max(w_1+⋅⋅⋅+w_{i−1}−s_i) max(w1 + ⋅⋅⋅ + wi − 1 − si) is the smallest, and record this value as val.

In order to find the sorting scheme, you can exchange the positions of i, i+1 cattle to see what equivalent conditions are satisfied, so that the val after exchange is not larger than before.

Because s and W are positive numbers, w i − s i + 1 > − s i + 1 w_i−s_{i+1}>−s_{i+1} wi​−si+1​>−si+1​ , w i + 1 − s i > − s i w_{i+1}−s_i>−s_i wi+1​−si​>−si​
compare w i − s i + 1 w_i−s_{i+1} wi − si+1 − and w i + 1 − s i w_{i+1}−s_{i} wi+1 − si +

So we get the method: sort by w + s of each cow, and exchange when there is reverse order (i.e. ascending order),
Then calculate the dangerous value of each cow according to the meaning of the question, and record the maximum value

125. Acrobatic cow - AcWing question bank

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;
typedef long long ll;
int n;
const int MAXN = 50050;
ll sum, ans;
struct Cow{
    int s, w;
    bool operator<(const Cow &a)
    {
        return s+w < a.s+a.w;
    }
}cow[MAXN];

int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i++)
    {
        scanf("%d%d",&cow[i].w,&cow[i].s);
    }
    sort(cow,cow+n);
    ans -= cow[0].s;
    sum = cow[0].w;
    for(int i = 1;i < n;i++)
    {
        if(sum - cow[i].s > ans) ans = sum - cow[i].s;
        sum += cow[i].w;
    }
    printf("%lld\n",ans);
    return 0;
}

7. Spatiotemporal complexity analysis

Generally, the time limit of ACM or written test questions is 1 second or 2 seconds.
In this case, the number of operations in C + + code is controlled to 1 0 7 ∼ 1 0 8 10^7∼10^8 107 ∼ 108 is the best.

The time complexity of the code and how to select the algorithm under different data ranges are given below:

[external chain picture transferring... (img-Y0yz0FNM-1629167397793)]