Search and graph theory (2)

This section is about the shortest path.

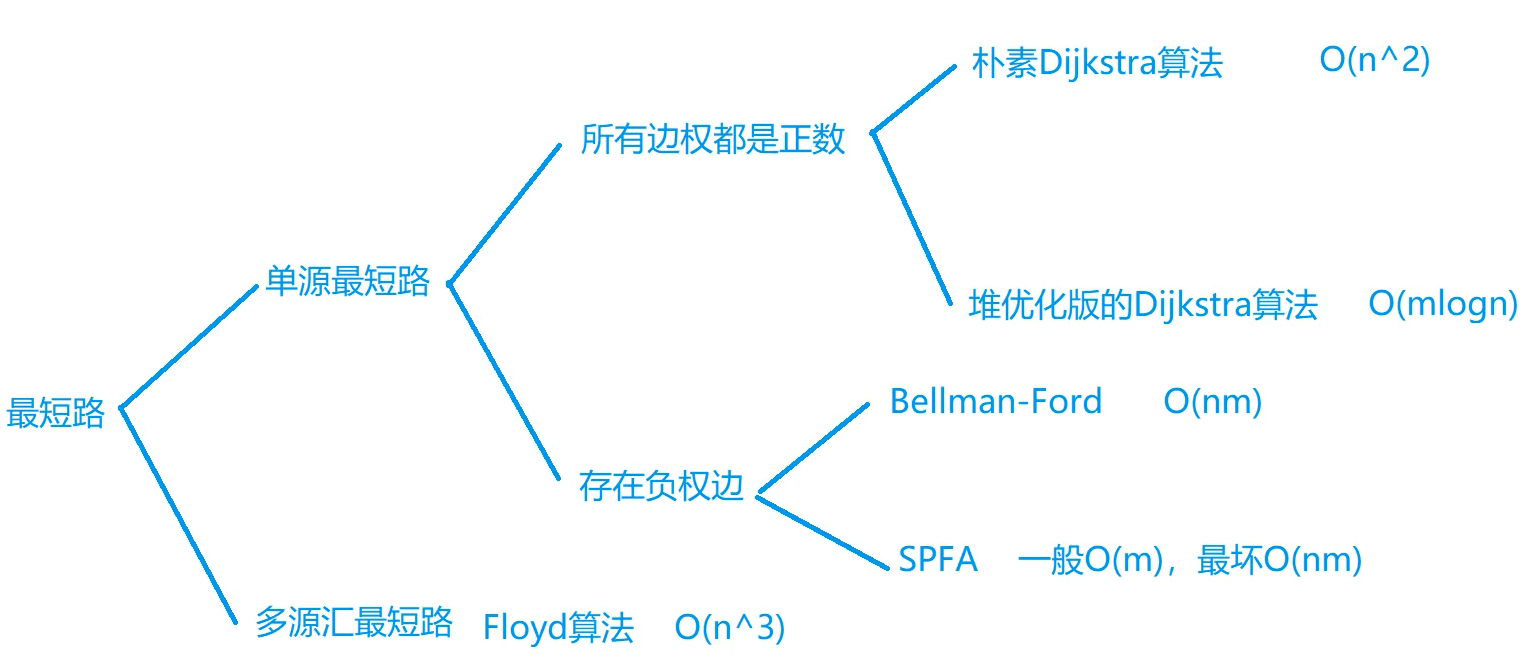
The most common short circuit problems are generally divided into two categories:

• Single source shortest circuit
• Multi source sink shortest path

In the shortest path problem, the source point is the starting point and the sink point is the end point.

Single source shortest circuit

Single source shortest path refers to finding the shortest distance from one point to all other points. (the starting point is fixed and single)

According to whether there is an edge with negative weight, it can be divided into two cases

• All edges have positive weights

  There are usually two algorithms

  • Plain Dijkstra

    Time complexity O(n2), where n is the number of vertices in the graph and m is the number of edges

  • Heap optimized version of Dijkstra

    Time complexity O(mlogn)

  Which is better or worse depends on the density of the graph (depends on the relationship between the number of points n and the number of edges m). When it is a sparse graph (N and m are at the same level), the heap optimized version of Dijkstra may be better. When it is a dense graph (M and n2 are at the same level), it is better to use naive Dijkstra.

• There are edges with negative weights

  There are usually two algorithms

  • Bellman-Ford

    Time complexity O(nm)

  • SPFA

    The time complexity is generally O(m) and the worst O(nm), which is the optimized version of the former. However, in some cases, SPFA cannot be used, and the former can only be used. For example, the shortest circuit is required to not exceed k edges. At this time, Bellman Ford can only be used

Multi source sink shortest circuit

Find the shortest path from multiple starting points to other points. (the starting point is not fixed, but multiple)

Floyd algorithm (time complexity O(n3))

The core of the shortest path problem is to abstract the problem into a shortest path problem and build a graph. The problems related to graph theory do not focus on the principle of algorithm, but on the abstraction of the problem.

Dijkstra is based on greed, Floyd is based on dynamic programming, and Bellman Ford is based on discrete mathematics.

Selection of algorithm: Generally speaking, Dijkstra is used for the shortest path of single source, if there is no negative weight edge, SPFA is usually used for those with negative weight edge, and Bellman Ford is rarely used; For the multi-source shortest circuit, use Floyd.

Algorithm idea

Plain Dijkstra

Suppose there are n points in the graph with subscripts 1~n. The distance of a point mentioned below refers to the distance from the point to the starting point (point 1).

The algorithm steps are as follows: a set s is used to store the points whose shortest distance has been determined.

1. Initialization distance, d[1] = 0, d[i] = + ∞. That is, the distance of the starting point is initialized to 0, while the distance of other points is not determined at present, which is represented by positive infinity.

2. loop

   Each time, from the points with known distance, select a point that is not in the s set and has the shortest distance (this step can be optimized with a small root heap), traverse all the edges of the point, and update the distance of the points connected by these edges. And add the selected point to the set s, because the shortest distance of the point has been determined at this time.

3. When all points are added to s, it means that the shortest distance of all points has been determined

Note that the known distance of a point does not mean that the distance of this point is the final shortest distance. In the subsequent cycle, a shorter path may be used to update.

Exercise: acwing - 849: Dijkstra finding the shortest path I

Problem solving (C + +)

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f; // Positive infinity
int g[N][N]; // Dense graphs are stored by adjacency matrix
int d[N]; // distance
int n, m;
bool visited[N];

int dijkstra() {
	d[1] = 0;
	// every time
	for(int i = 1; i <= n; i++) {
		//Find a point with the smallest distance from the starting point
		int t = 0; // d[0] is not used and its value is always INF
		for(int j = 1; j <= n; j++) {
			if(!visited[j] && d[j] < d[t]) {
				t = j;
			}
		}
		if(t == 0) break; // No point found, break in advance
		// Find the point
		visited[t] = true; // Put into set s
		// Update the distance of all other points
		for(int i = 1; i <= n; i++) {
			d[i] = min(d[i], d[t] + g[t][i]);
		}
	}
	if(d[n] == INF) return -1;
	else return d[n];
}

int main() {
	// initialization
	memset(d, 0x3f, sizeof d);
	memset(g, 0x3f, sizeof g);
	scanf("%d%d", &n, &m);
	while(m--) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		g[x][y] = min(g[x][y], z); // Repeat edges only need to keep one with the smallest weight
	}
	printf("%d", dijkstra());
	return 0;
}

Problem solving (Java)

import java.util.Arrays;
import java.util.Scanner;

/**
 * @Author yogurtzzz
 * @Date 2021/6/25 9:01
 *
 * Dense graph, stored using adjacency matrix
 **/
public class Main {

	static final int INF = 0x3f3f3f3f;

	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		int n, m;
		n = scanner.nextInt();
		m = scanner.nextInt();
		int[][] g = new int[n + 1][n + 1]; // Adjacency matrix storage of Graphs
		for(int i = 0; i < n + 1; i++) {
			for (int j = 0; j < n + 1; j++) g[i][j] = INF; // Initialize all distances to positive infinity
		}
		while(m-- > 0) {
			int x, y, z;
			x = scanner.nextInt();
			y = scanner.nextInt();
			z = scanner.nextInt();
			g[x][y] = Math.min(g[x][y], z); // Solve the multiple edges and keep the edge with the minimum distance
		}
		System.out.println(dijkstra(g, n));
	}

	/**
	 * @param g Adjacency matrix representation of Graphs
	 * @param n Number of points in the graph
	 * **/
	static int dijkstra(int[][] g, int n) {
		int[] distance = new int[n + 1];
		boolean[] visited = new boolean[n + 1]; //state variable
		Arrays.fill(distance, INF); // Initialization distance is positive infinity
		distance[1] = 0; // The distance from the starting point is 0
		// Cycle n times
		for (int i = 0; i < n; i++) {
			// First find the point with the smallest distance
			int min = 0;
			for(int j = 1; j <= n; j++) {
				if (!visited[j] && distance[j] < distance[min]) {
					min = j;
				}
			}
			if (min == 0) break; // All points are traversed to the end
			// The point with the smallest distance was found
			visited[min] = true; // This is to solve the self ring
			// Update distance, enumerate all columns
			for(int j = 1; j <= n; j++) {
				// When there is an out edge, its distance is updated
				if (g[min][j] != INF) distance[j] = Math.min(distance[j], distance[min] + g[min][j]);
			}
		}
		if (distance[n] == INF) return -1;
		else return distance[n];
	}
}

Heap optimized Dijkstra

The heap can be written by itself (simulated by array) or ready-made (priority_queue is provided in STL of C + + and priority queue is provided in JDK of Java)

Exercise: acwing - 850: Dijkstra finding the shortest path II

Solution: handwriting heap (C + +)

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
// Sparse graph is stored with adjacency table, and Dijkstra with heap optimization is selected
const int N = 2e5;
const int INF = 0x3f3f3f3f;  // Positive infinity

int h[N], e[N], w[N], ne[N], idx; // Adjacency table storage, - 1 indicates an empty node
int d[N]; // distance
bool visited[N]; // state
int n, m;

int hVal[N], hDis[N], hSize; // Array analog heap, hVal storage node number, hDis storage node distance
int ph[N], hp[N]; // Record the mapping relationship between the node subscript in the heap and the node number in the graph

// Swap 2 subscripts, which are subscripts in the heap
void heap_swap(int a, int b) {
	swap(hp[a], hp[b]); 
	swap(ph[hp[a]], ph[hp[b]]);
	swap(hVal[a], hVal[b]);
	swap(hDis[a], hDis[b]);
}

// Adjust upward, remember to adjust according to the distance hDis
void up(int pos) {
	while(pos / 2 >= 1 && hDis[pos / 2] > hDis[pos]) {
		heap_swap(pos, pos / 2);
		pos /= 2; // Write this line less and look for an hour!
	}
}

// Adjust downward, remember to adjust according to the distance hDis
void down(int pos) {
	int min = pos;
	if(2 * pos <= hSize && hDis[2 * pos] < hDis[min]) min = 2 * pos;
	if(2 * pos + 1 <= hSize && hDis[2 * pos + 1] < hDis[min]) min = 2 * pos + 1;
	if(min != pos) {
		heap_swap(pos, min);
		down(min);
	}
}

// Get and pop up the heap top node
int pop() {
	if(hSize == 0) return 0; // The heap is empty
	int res = hVal[1]; // Node number
	heap_swap(1, hSize); // Swap top and tail
	hSize--; //
	down(1); // Adjustment reactor 
	return res;
}

// Insert a node into the heap, where x is the node number and dis is the distance from the node to the starting point
void insert_to_heap(int x, int dis) {
	// Subscript starts with 1
	hSize++;
	ph[x] = hSize;
	hp[hSize] = x;
	// Insert a count to the heap
	hVal[hSize] = x; // Record node number
	hDis[hSize] = dis; // Record node distance
	up(hSize); // Upward adjustment
}

// Connect an edge between x and y, and the weight is z
void add(int x, int y, int z) {
    // Record the edge to the adjacency table
	e[idx] = y;
	w[idx] = z;
	ne[idx] = h[x];
	h[x] = idx++;
}

int dijkstra() {
	d[1] = 0; // Initialization, starting point (point 1) distance is 0
	insert_to_heap(1, 0); // Insert start point into heap
	for(int i = 1; i <= n; i++) {
		// One node at a time
		int t = pop(); // Obtain the point with the shortest current distance, and the node number is 1~n
		if(t == 0) break; // There are no elements in the heap, indicating that all nodes have been accessed and ended in advance
		if(visited[t]) continue; // This point is already in the set s. skip it directly
		visited[t] = true;
		// Update the distance of all points out of the edge
		for(int j = h[t]; j != -1; j = ne[j]) {
			int u = e[j]; // Node number
			int du = w[j]; // Side length
			if(d[u] > d[t] + w[j]) {
			    d[u] = d[t] + w[j];
			    insert_to_heap(u, d[u]); // Duplicate points can also be inserted directly. It doesn't matter
			}
		}
	}
	if(d[n] == INF) return -1;
	else return d[n];
}


int main() {
	memset(h, -1, sizeof h); // initialization
	memset(d, 0x3f, sizeof d); // Distance initialized to INF
	memset(hVal, 0, sizeof hVal);
	memset(hDis, 0, sizeof hDis);
	scanf("%d%d", &n, &m);
	while(m--) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		add(x, y, z);
	}
	printf("%d", dijkstra());
	return 0;
}

Problem solving: using off the shelf heap (Java)

import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Scanner;

/**
 * @Author yogurtzzz
 * @Date 2021/6/25 9:33
 *
 * Heap optimized version of Dijkstra
 * Sparse graph, stored with adjacent linked list
 **/
public class Main {
	
	static class Pair {
		int first;
		int second;

		Pair(int first, int second) {
			this.first = first;
			this.second = second;
		}
	}

	static Scanner scanner = new Scanner(System.in);
	
	static int INF = 0x3f3f3f3f;

	static final int N = 200000;

	static int[] h;
	static int[] e = new int[N], w = new int[N], ne = new int[N];// Graph adjacency table representation, array simulation linked list
	static int idx; // Used to assign linked list nodes
	
	public static void main(String[] args) {
		int n = readInt(), m = readInt();
		h = new int[n + 1];
		Arrays.fill(h, -1); // Initialization, all adjacent lists are - 1, indicating an empty linked list
		while(m-- > 0) {
			int x = readInt(), y = readInt(), z = readInt();
			add(x, y, z);
		}
		System.out.println(dijkstra(n));
	}
	
	private static int dijkstra(int n) {
		int[] distance = new int[n + 1];
		boolean[] visited = new boolean[n + 1];
		Arrays.fill(distance, INF);
		distance[1] = 0; // Initialize start distance
		// Small root pile
		PriorityQueue<Pair> heap = new PriorityQueue<>(Comparator.comparingInt(o -> o.first));
		heap.offer(new Pair(0, 1));  // Insert the starting point into the heap. first is the distance and second is the node number
		for(int i = 0; i < n; i++) {
			Pair p = heap.poll(); // Gets the node with the smallest current distance
			if (p == null) break; // There are no elements in the heap. It ends early
			int nodeNo = p.second, nodeDis = p.first; // Get the number and distance of the node
			visited[nodeNo] = true; // Solve self loop
			for(int j = h[nodeNo]; j != -1; j = ne[j]) {
				// Obtain all the outgoing edges of the node from the adjacency table and update them in turn
				int nextNodeNo = e[j];
				int nextNodeWeight = w[j];
				if (distance[nextNodeNo] > nodeDis + nextNodeWeight) {
					// to update
					distance[nextNodeNo] = nodeDis + nextNodeWeight;
					// Insert into heap
					heap.offer(new Pair(distance[nextNodeNo], nextNodeNo));
				}
			}
		}
		return distance[n] == INF ? -1 : distance[n];
	}
	
	// Add an edge
	private static void add(int x, int y, int z) {
		e[idx] = y;
		w[idx] = z;
		ne[idx] = h[x];
		h[x] = idx++;
	}

	private static int readInt() {
		return scanner.nextInt();
	}
}

Bellman-Ford

Algorithm idea

Cycle n times

Each loop traverses all the edges in the graph. Update d[b] = min(d[b], d[a] + w) for each edge (a, b, w), (referring to an edge with weight W from point a to point B)

(you can define a class or a structure in C + + to store a, b and W. it means that there is an edge, a point points to b point, and the weight is w). When traversing all edges, you only need to traverse all the structure arrays

Meaning of the number of cycles: suppose K cycles, the shortest distance from the starting point to each point through no more than k edges.

The algorithm can ensure that D [b] < = D [a] + W is satisfied for all edges (a, b, w) after n cycles. This inequality is called trigonometric inequality. The above update operation is called slack operation.

The algorithm is suitable for the case of negative weight edges.

Note: if there is a negative weight circuit, the shortest circuit does not necessarily exist. (note that it does not necessarily exist). When the negative weight loop is on the path from point 1 to point n, the distance will decrease every time you walk along the negative weight loop, and you can go on indefinitely, and the distance from point 1 to point n will become infinitely small (negative infinity)

The algorithm can find out whether there is a negative weight loop in the graph. If an update is performed for the nth iteration, it indicates that there is a shortest path passing through n edges. Since there are only n points and N edges need n+1 points, it indicates that there must be two points in the N edges that are the same, it indicates that there are rings and rings on the path, and the update is performed this time, indicating that the weight of the ring is negative. However, SPFA algorithm is usually used to solve the negative weight loop instead of Bellman Ford algorithm, because the latter has lower time complexity.

Since the loop is repeated N times, all edges (m edges) are traversed each time. Then the time complexity of Bellman Ford algorithm is O(n) × m).

Exercise: acwing - 853: shortest path with side limit

#include<iostream>
#include<cstring>
using namespace std;

const int N = 510, M = 10010;
const int INF = 0x3f3f3f3f;
struct Edge
{
	int a, b, w;
} edge[M]; // Directly use the structure to store all edges

int n, m, k, d[N], tmp[N];

void bellman_ford() {
	memset(d, 0x3f, sizeof d);
	d[1] = 0; // initialization
	for(int i = 0; i < k; i++) {
		memcpy(tmp, d, sizeof d); // Backup required
		for(int j = 0; j < m; j++) {
			Edge e = edge[j];
			int a = e.a, b = e.b, w = e.w;
			if(tmp[a] == INF) continue;
			if(d[b] > tmp[a] + w) { // Use the last d for calculation to prevent series connection
				// to update
				d[b] = tmp[a] + w;
			}
		}
	}
	if(d[n] == INF) printf("impossible");
	else printf("%d", d[n]);
}

int main() {
	scanf("%d%d%d", &n, &m, &k);
	for(int i = 0; i < m; i++) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		edge[i] = {x, y, z};
	}
	bellman_ford();
	return 0;
}

SPFA

If SPFA algorithm is to be used, there must be no negative weight circuit in the diagram. SPFA can be used as long as there is no negative weight loop in the figure, and the limitation of this algorithm is relatively small.

SPFA is actually an optimization of Bellman Ford.

It optimizes this step: d[b] = min(d[b], d[a] + w)

We can observe that only when d[a] becomes smaller will d[b] be updated in the next cycle

Use BFS for optimization. A queue is used to store nodes with smaller distance.

(much like Dijkstra)

Exercise: acwing - 851: spfa finding the shortest path

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;

// Because of the need to use out edges, the adjacency table is used to store the graph
int h[N], e[N], w[N], ne[N], idx;

int d[N]; // Storage distance

int n, m;

void add(int x, int y, int z) {
	e[idx] = y;
	w[idx] = z;
	ne[idx] = h[x];
	h[x] = idx++;
}

void spef() {
	memset(d, 0x3f, sizeof d); // Initialization distance
	d[1] = 0;
	queue<int> q;
	q.push(1);
	while(!q.empty()) {
		int t = q.front();
		q.pop();
		for(int i = h[t]; i != -1; i = ne[i]) {
			// Update all out edges
			int j = e[i];
			if(d[j] > d[t] + w[i]) {
				d[j] = d[t] + w[i];
				q.push(j);
			}
		}
	}
	if(d[n] == INF) printf("impossible");
	else printf("%d", d[n]);
}

int main() {
	scanf("%d%d", &n, &m);
	memset(h, -1, sizeof h); // Initialize the adjacency list, all of which are empty linked lists
	while(m--) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		add(x, y, z);
	}
	spef();
	return 0;
}

Advantages of SPFA: it can solve the problem of no negative weight edge and the problem of negative weight edge, and the efficiency is relatively high. However, when the shortest path problem with no more than k edges is required, the bellman Ford algorithm can only be used.

Exercise: acwing - 852: spfa finding negative rings

The basic idea is to add a variable int ctn[N] to record the length of the edges passing through the i-th point. If the number of edges reaching a point is greater than N, it indicates that there is a negative weight circuit

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;

// Because of the need to use the edge, the adjacency table is used to store the graph
int h[N], e[N], w[N], ne[N], idx;

int d[N]; // Storage distance
int ctn[N];
bool visited[N];

int n, m;

void add(int x, int y, int z) {
	e[idx] = y;
	w[idx] = z;
	ne[idx] = h[x];
	h[x] = idx++;
}

void spef() {
	queue<int> q;
	for(int i = 1; i <= n; i++) {
		q.push(i);
		visited[i] = true;
	}
	memset(d, 0x3f, sizeof d); // Initialization distance
	d[1] = 0;
	while(!q.empty()) {
		int t = q.front();
		q.pop();
		visited[t] = false;
		for(int i = h[t]; i != -1; i = ne[i]) {
			// Update all outgoing edges
			int j = e[i];
			if(d[j] > d[t] + w[i]) {
				d[j] = d[t] + w[i];
				ctn[j] = ctn[t] + 1;
				if(ctn[j] >= n) {
					printf("Yes");
					return;
				}
				if(!visited[j]) q.push(j);
			}
		}
	}
	printf("No");
}

int main() {
	scanf("%d%d", &n, &m);
	memset(h, -1, sizeof h); // Initialize the adjacency list, all of which are empty linked lists
	while(m--) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		add(x, y, z);
	}
	spef();
	return 0;
}

Floyd

Solving the shortest path problem of multiple sources and sinks can also deal with the case of negative edge weight, but it can not deal with the case of negative weight circuit.

Use adjacency matrix to store graphs. Initially, d[i][j] is used to store the graph and store all edges

Algorithm idea: three-layer loop

for(k = 1; k <= n; k++)

​ for(i = 1; i <= n; i++)

​ for(j = 1; j <= n; j++)

​ d[i,j] = min(d[i,j] , d[i,k] + d[k,j])

At the end of the cycle, d[i][j] stores the shortest distance from point I to j.

The principle is based on dynamic planning (the specific principle will be explained in detail in the subsequent dynamic planning chapter).

The state representation is: d(k, i, j), the shortest distance from point i to point j only through the intermediate points of 1 ~ k

Exercise: acwing - 854: Floyd finding the shortest path

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 210, INF = 0x3f3f3f3f;
int g[N][N]; // Adjacency matrix storage
int n, m, k;

void floyd() {
	for(int p = 1; p <= n; p++) {
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= n; j++) {
				if(g[i][p] != INF && g[p][j] != INF) g[i][j] = min(g[i][j], g[i][p] + g[p][j]);
			}
		}
	}
}

int main() {
	scanf("%d%d%d", &n, &m, &k);
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) {
			if(i == j) g[i][j] = 0;
			else g[i][j] = INF;
		}
	}
	while(m--) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		g[x][y] = min(g[x][y], z); // Handle heavy edges
	}
	floyd();
	while(k--) {
		int x, y;
		scanf("%d%d", &x, &y);
		if(g[x][y] == INF) printf("impossible\n");
		else printf("%d\n", g[x][y]);
	}
	return 0;
}