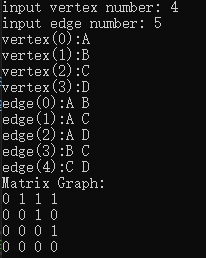
Adjacency matrix (note the directed adjacency matrix graph implemented here)
The adjacency matrix of a graph is stored in two arrays. A one-dimensional array stores the vertex information in the graph, and a two-dimensional array (adjacency matrix) stores the edge or arc information in the graph.
Let graph G have n vertices, then the adjacency matrix is a square matrix of nn, which is defined as:
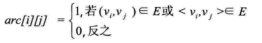
Look at an example. The left side of the figure below is an undirected graph.
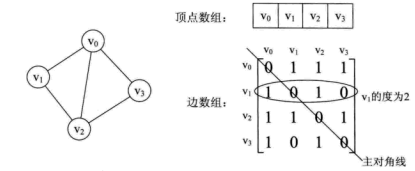
As can be seen from the above, the edge array of an undirected graph is a symmetric matrix. The so-called symmetric matrix is that the elements of the n-order matrix satisfy aij = aji. That is, the main diagonal from the upper left corner to the lower right corner of the matrix is the axis, and the elements in the upper right corner and the corresponding elements in the lower left corner are all equal.
From this matrix, it is easy to know the information in the figure.
(1) It is easy to judge whether any two vertices have edges or not;
(2) You should know that the degree of a vertex is actually the sum of the elements of the vertex vi in row i or column i of the adjacency matrix;
(3) To find all adjacent points of vertex vi is to scan the elements in the ith row of the matrix, and arc[i][j] is 1, which is the adjacent point;
The directed graph pays attention to the in degree and out degree. The in degree of vertex vi is 1, which is exactly the sum of the numbers in column i. The exitance of vertex vi is 2, that is, the sum of the numbers in row i.
If graph G is a network graph with n vertices, the adjacency matrix is a square matrix of nn, which is defined as:
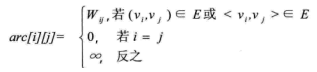
The difference between adjacency table and adjacency matrix:
For an undirected graph with n vertices and e edges
Its adjacency table represents n vertex table nodes and 2e edge table nodes
For a directed graph with n vertices and e edges
Its adjacency table represents n vertex table nodes and e edge table nodes
If the number of edges in a graph is much less than n^2, it is called sparse graph, which saves space by using adjacency table than adjacency matrix
If the number of edges in a graph is close to n^2, an undirected graph close to n*(n-1) is called a dense graph. Considering the chain domain to be added to the adjacency table, the adjacency matrix representation is appropriate
Code implementation of adjacency matrix (note the directed adjacency matrix diagram implemented here) (C + +):
/*
Adjacency matrix
@author lph
@date 2022/02/24
*/
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;
constexpr auto MAX = 100;
class MatrixDG {
private:
char mVexs[MAX]; // Vertex set
int mVexNum; // Number of vertices
int mEdgNum; // Number of sides
int mMatrix[MAX][MAX]; // adjacency matrix
public:
// Create diagram (input data by yourself)
MatrixDG();
// Create diagram (with provided matrix)
MatrixDG(char vexs[], int vlen, char edges[][2], int elen);
~MatrixDG();
// Print matrix queue diagram
void print();
private:
// Read an input character
char readChar();
// Returns the position of ch in the mMatrix matrix
int getPosition(char ch);
};
/*
Create diagram (input data by yourself)
*/
MatrixDG::MatrixDG() {
char c1, c2;
int i, p1, p2;
// Enter the number of vertices and edges
cout << "input vertex number: ";
cin >> mVexNum;
cout << "input edge number: ";
cin >> mEdgNum;
if (mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum - 1)))) {
cout << "input error: invalid parameters!" << endl;
return;
}
// Initialize vertex
for (i = 0; i < mVexNum; ++i) {
cout << "vertex(" << i << "):";
mVexs[i] = readChar();
}
// Initialize edge
// First initialize the edges from all starting vertices to other vertices to 0
for (i = 0; i < mVexNum; i++)
{
for (int j = 0; j < mVexNum; ++j)
mMatrix[i][j] = 0;
}
for (i = 0; i < mEdgNum; ++i) {
// Reads the start and end vertices of the edge
cout << "edge(" << i << "):";
c1 = readChar();
c2 = readChar();
p1 = getPosition(c1);
p2 = getPosition(c2);
if (p1 == -1 || p2 == -1) {
cout << "input error: invalid edge!" << endl;
return;
}
mMatrix[p1][p2] = 1;
}
}
/*
Create diagram (using existing matrix)
Parameter Description:
vexs -- vertex array
vlen -- Length of vertex array
edges -- Edge array
elen -- Length of edge array
*/
MatrixDG::MatrixDG(char vexs[], int vlen, char edges[][2], int elen) {
int i, p1, p2;
// Initializes the number of vertices and edges
mVexNum = vlen;
mEdgNum = elen;
// Initialize vertex
for (i = 0; i < mVexNum; ++i)
mVexs[i] = vexs[i];
// Initialize edge
// First initialize the edges from all starting vertices to other vertices to 0
for (i = 0; i < mVexNum; i++)
{
for (int j = 0; j < mVexNum; ++j)
mMatrix[i][j] = 0;
}
for (i = 0; i < mEdgNum; ++i) {
// Reads the start and end vertices of the edge
p1 = getPosition(edges[i][0]);
p2 = getPosition(edges[i][1]);
mMatrix[p1][p2] = 1;
}
}
/*
Destructor
*/
MatrixDG::~MatrixDG() {
}
/*
Returns the position of ch in the mMatrix matrix
*/
int MatrixDG::getPosition(char ch) {
int i;
for (i = 0; i < mVexNum; ++i)
if (mVexs[i] == ch)
return i;
return -1;
}
/*
Read an input character
*/
char MatrixDG::readChar() {
char ch;
do {
cin >> ch;
} while (!((ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z')));
return ch;
}
/*
Print matrix queue diagram
*/
void MatrixDG::print() {
int i, j;
cout << "Matrix Graph:" << endl;
for (i = 0; i < mVexNum; ++i) {
for (j = 0; j < mVexNum; ++j)
cout << mMatrix[i][j] << " ";
cout << endl;
}
}
int main() {
char vexs[] = { 'A', 'B', 'C', 'D', 'E', 'D', 'F', 'G' };
char edges[][2] = {
{'A', 'B'},
{'B', 'C'},
{'B', 'E'},
{'B', 'F'},
{'C', 'E'},
{'D', 'C'},
{'E', 'B'},
{'E', 'D'},
{'F', 'G'}
};
int vlen = sizeof(vexs) / sizeof(vexs[0]);
int elen = sizeof(edges) / sizeof(edges[0]);
MatrixDG* pG;
// Custom chart (input matrix queue)
//pG = new MatrixDG();
// Use existing data
pG = new MatrixDG(vexs, vlen, edges, elen);
// Print results
pG->print();
return 0;
}Print results (note the directed adjacency matrix diagram implemented here):
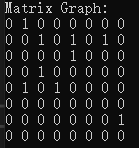
Print the data input by yourself (note the directed adjacency matrix diagram implemented here):