Higher order data structure
Splay
AcWing 2437. Splay
AcWing 950.Depressed teller
AcWing 1063.Never Township
AcWing 955.Maintain columns

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 500010, INF = 1e9;
int n, m;
struct Node
{
int s[2], p, v;
int rev, same;
int size, sum, ms, ls, rs;
void init(int _v, int _p)
{
s[0] = s[1] = 0, p = _p, v = _v;
rev = same = 0;
size = 1, sum = ms = v;
ls = rs = max(v, 0);
}
}tr[N];
int root, nodes[N], tt;
int w[N];
void pushup(int x)
{
auto &u = tr[x], &l = tr[u.s[0]], &r = tr[u.s[1]];
u.size = l.size + r.size + 1;
u.sum = l.sum + r.sum + u.v;
u.ls = max(l.ls, l.sum + u.v + r.ls);
u.rs = max(r.rs, r.sum + u.v + l.rs);
u.ms = max(max(l.ms, r.ms), l.rs + u.v + r.ls);
}
void pushdown(int x)
{
auto &u = tr[x], &l = tr[u.s[0]], &r = tr[u.s[1]];
if (u.same)
{
u.same = u.rev = 0;
if (u.s[0]) l.same = 1, l.v = u.v, l.sum = l.v * l.size;
if (u.s[1]) r.same = 1, r.v = u.v, r.sum = r.v * r.size;
if (u.v > 0)
{
if (u.s[0]) l.ms = l.ls = l.rs = l.sum;
if (u.s[1]) r.ms = r.ls = r.rs = r.sum;
}
else
{
if (u.s[0]) l.ms = l.v, l.ls = l.rs = 0;
if (u.s[1]) r.ms = r.v, r.ls = r.rs = 0;
}
}
else if (u.rev)
{
u.rev = 0, l.rev ^= 1, r.rev ^= 1;
swap(l.ls, l.rs), swap(r.ls, r.rs);
swap(l.s[0], l.s[1]), swap(r.s[0], r.s[1]);
}
}
void rotate(int x)
{
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x, int k)
{
while (tr[x].p != k)
{
int y = tr[x].p, z = tr[y].p;
if (z != k)
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
rotate(x);
}
if (!k) root = x;
}
int get_k(int k)
{
int u = root;
while (u)
{
pushdown(u);
if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0];
else if (tr[tr[u].s[0]].size + 1 == k) return u;
else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1];
}
}
int build(int l, int r, int p)
{
int mid = l + r >> 1;
int u = nodes[tt -- ];
tr[u].init(w[mid], p);
if (l < mid) tr[u].s[0] = build(l, mid - 1, u);
if (mid < r) tr[u].s[1] = build(mid + 1, r, u);
pushup(u);
return u;
}
void dfs(int u)
{
if (tr[u].s[0]) dfs(tr[u].s[0]);
if (tr[u].s[1]) dfs(tr[u].s[1]);
nodes[ ++ tt] = u;
}
int main()
{
for (int i = 1; i < N; i ++ ) nodes[ ++ tt] = i;
scanf("%d%d", &n, &m);
tr[0].ms = w[0] = w[n + 1] = -INF;
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
root = build(0, n + 1, 0);
char op[20];
while (m -- )
{
scanf("%s", op);
if (!strcmp(op, "INSERT"))
{
int posi, tot;
scanf("%d%d", &posi, &tot);
for (int i = 0; i < tot; i ++ ) scanf("%d", &w[i]);
int l = get_k(posi + 1), r = get_k(posi + 2);
splay(l, 0), splay(r, l);
int u = build(0, tot - 1, r);
tr[r].s[0] = u;
pushup(r), pushup(l);
}
else if (!strcmp(op, "DELETE"))
{
int posi, tot;
scanf("%d%d", &posi, &tot);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
dfs(tr[r].s[0]);
tr[r].s[0] = 0;
pushup(r), pushup(l);
}
else if (!strcmp(op, "MAKE-SAME"))
{
int posi, tot, c;
scanf("%d%d%d", &posi, &tot, &c);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
auto& son = tr[tr[r].s[0]];
son.same = 1, son.v = c, son.sum = c * son.size;
if (c > 0) son.ms = son.ls = son.rs = son.sum;
else son.ms = c, son.ls = son.rs = 0;
pushup(r), pushup(l);
}
else if (!strcmp(op, "REVERSE"))
{
int posi, tot;
scanf("%d%d", &posi, &tot);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
auto& son = tr[tr[r].s[0]];
son.rev ^= 1;
swap(son.ls, son.rs);
swap(son.s[0], son.s[1]);
pushup(r), pushup(l);
}
else if (!strcmp(op, "GET-SUM"))
{
int posi, tot;
scanf("%d%d", &posi, &tot);
int l = get_k(posi), r = get_k(posi + tot + 1);
splay(l, 0), splay(r, l);
printf("%d\n", tr[tr[r].s[0]].sum);
}
else printf("%d\n", tr[root].ms);
}
return 0;
}
Tree Cover Tree
AcWing 2488.Tree Nest Tree - Simple Edition
AcWing 2476.Tree Cover Tree

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2000010, INF = 1e9;
int n, m;
struct Node
{
int s[2], p, v;
int size;
void init(int _v, int _p)
{
v = _v, p = _p;
size = 1;
}
}tr[N];
int L[N], R[N], T[N], idx;
int w[N];
void pushup(int x)
{
tr[x].size = tr[tr[x].s[0]].size + tr[tr[x].s[1]].size + 1;
}
void rotate(int x)
{
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int& root, int x, int k)
{
while (tr[x].p != k)
{
int y = tr[x].p, z = tr[y].p;
if (z != k)
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
rotate(x);
}
if (!k) root = x;
}
void insert(int& root, int v)
{
int u = root, p = 0;
while (u) p = u, u = tr[u].s[v > tr[u].v];
u = ++ idx;
if (p) tr[p].s[v > tr[p].v] = u;
tr[u].init(v, p);
splay(root, u, 0);
}
int get_k(int root, int v)
{
int u = root, res = 0;
while (u)
{
if (tr[u].v < v) res += tr[tr[u].s[0]].size + 1, u = tr[u].s[1];
else u = tr[u].s[0];
}
return res;
}
void update(int& root, int x, int y)
{
int u = root;
while (u)
{
if (tr[u].v == x) break;
if (tr[u].v < x) u = tr[u].s[1];
else u = tr[u].s[0];
}
splay(root, u, 0);
int l = tr[u].s[0], r = tr[u].s[1];
while (tr[l].s[1]) l = tr[l].s[1];
while (tr[r].s[0]) r = tr[r].s[0];
splay(root, l, 0), splay(root, r, l);
tr[r].s[0] = 0;
pushup(r), pushup(l);
insert(root, y);
}
void build(int u, int l, int r)
{
L[u] = l, R[u] = r;
insert(T[u], -INF), insert(T[u], INF);
for (int i = l; i <= r; i ++ ) insert(T[u], w[i]);
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
int query(int u, int a, int b, int x)
{
if (L[u] >= a && R[u] <= b) return get_k(T[u], x) - 1;
int mid = L[u] + R[u] >> 1, res = 0;
if (a <= mid) res += query(u << 1, a, b, x);
if (b > mid) res += query(u << 1 | 1, a, b, x);
return res;
}
void change(int u, int p, int x)
{
update(T[u], w[p], x);
if (L[u] == R[u]) return;
int mid = L[u] + R[u] >> 1;
if (p <= mid) change(u << 1, p, x);
else change(u << 1 | 1, p, x);
}
int get_pre(int root, int v)
{
int u = root, res = -INF;
while (u)
{
if (tr[u].v < v) res = max(res, tr[u].v), u = tr[u].s[1];
else u = tr[u].s[0];
}
return res;
}
int get_suc(int root, int v)
{
int u = root, res = INF;
while (u)
{
if (tr[u].v > v) res = min(res, tr[u].v), u = tr[u].s[0];
else u = tr[u].s[1];
}
return res;
}
int query_pre(int u, int a, int b, int x)
{
if (L[u] >= a && R[u] <= b) return get_pre(T[u], x);
int mid = L[u] + R[u] >> 1, res = -INF;
if (a <= mid) res = max(res, query_pre(u << 1, a, b, x));
if (b > mid) res = max(res, query_pre(u << 1 | 1, a, b, x));
return res;
}
int query_suc(int u, int a, int b, int x)
{
if (L[u] >= a && R[u] <= b) return get_suc(T[u], x);
int mid = L[u] + R[u] >> 1, res = INF;
if (a <= mid) res = min(res, query_suc(u << 1, a, b, x));
if (b > mid) res = min(res, query_suc(u << 1 | 1, a, b, x));
return res;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
build(1, 1, n);
while (m -- )
{
int op, a, b, x;
scanf("%d", &op);
if (op == 1)
{
scanf("%d%d%d", &a, &b, &x);
printf("%d\n", query(1, a, b, x) + 1);
}
else if (op == 2)
{
scanf("%d%d%d", &a, &b, &x);
int l = 0, r = 1e8;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (query(1, a, b, mid) + 1 <= x) l = mid;
else r = mid - 1;
}
printf("%d\n", r);
}
else if (op == 3)
{
scanf("%d%d", &a, &x);
change(1, a, x);
w[a] = x;
}
else if (op == 4)
{
scanf("%d%d%d", &a, &b, &x);
printf("%d\n", query_pre(1, a, b, x));
}
else
{
scanf("%d%d%d", &a, &b, &x);
printf("%d\n", query_suc(1, a, b, x));
}
}
return 0;
}
AcWing 2306.K Major Query
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 50010, P = N * 17 * 17, M = N * 4;
int n, m;
struct Tree
{
int l, r, sum, add;
}tr[P];
int L[M], R[M], T[M], idx;
struct Query
{
int op, a, b, c;
}q[N];
vector<int> nums;
int get(int x)
{
return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}
void build(int u, int l, int r)
{
L[u] = l, R[u] = r, T[u] = ++ idx;
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
int intersection(int a, int b, int c, int d)
{
return min(b, d) - max(a, c) + 1;
}
void update(int u, int l, int r, int pl, int pr)
{
tr[u].sum += intersection(l, r, pl, pr);
if (l >= pl && r <= pr)
{
tr[u].add ++ ;
return;
}
int mid = l + r >> 1;
if (pl <= mid)
{
if (!tr[u].l) tr[u].l = ++ idx;
update(tr[u].l, l, mid, pl, pr);
}
if (pr > mid)
{
if (!tr[u].r) tr[u].r = ++ idx;
update(tr[u].r, mid + 1, r, pl, pr);
}
}
void change(int u, int a, int b, int c)
{
update(T[u], 1, n, a, b);
if (L[u] == R[u]) return;
int mid = L[u] + R[u] >> 1;
if (c <= mid) change(u << 1, a, b, c);
else change(u << 1 | 1, a, b, c);
}
int get_sum(int u, int l, int r, int pl, int pr, int add)
{
if (l >= pl && r <= pr) return tr[u].sum + (r - l + 1) * add;
int mid = l + r >> 1, res = 0;
add += tr[u].add;
if (pl <= mid)
{
if (tr[u].l) res += get_sum(tr[u].l, l, mid, pl, pr, add);
else res += intersection(l, mid, pl, pr) * add;
}
if (pr > mid)
{
if (tr[u].r) res += get_sum(tr[u].r, mid + 1, r, pl, pr, add);
else res += intersection(mid + 1, r, pl, pr) * add;
}
return res;
}
int query(int u, int a, int b, int c)
{
if (L[u] == R[u]) return R[u];
int mid = L[u] + R[u] >> 1;
int k = get_sum(T[u << 1 | 1], 1, n, a, b, 0);
if (k >= c) return query(u << 1 | 1, a, b, c);
return query(u << 1, a, b, c - k);
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i ++ )
{
scanf("%d%d%d%d", &q[i].op, &q[i].a, &q[i].b, &q[i].c);
if (q[i].op == 1) nums.push_back(q[i].c);
}
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
build(1, 0, nums.size() - 1);
for (int i = 0; i < m; i ++ )
{
int op = q[i].op, a = q[i].a, b = q[i].b, c = q[i].c;
if (op == 1) change(1, a, b, get(c));
else printf("%d\n", nums[query(1, a, b, c)]);
}
return 0;
}
1782.Dynamic Ranking
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<map>
using namespace std;
const int N = 100010, M = 100010;
struct operation {
int kind, l, r, k, x, y, ans;
// kind = 1 means a query operation, otherwise a modification operation
}q[M];
int n, m;
int a[N], b[N << 1], len = 0, t[N << 1];
void msort(int head, int tail) {
if (head == tail) return;
int mid = (head + tail) >> 1;
msort(head, mid); msort(mid + 1, tail);
int pointer1 = head, pointer2 = mid + 1;
for (int i = 0; i < tail - head + 1; i++) {
if (pointer1 <= mid && pointer2 <= tail) {
if (b[pointer1] < b[pointer2]) t[i] = b[pointer1++];
else t[i] = b[pointer2++];
}
else if (pointer1 <= mid)t[i] = b[pointer1++];
else t[i] = b[pointer2++];
}
for (int i = 0; i < tail - head + 1; i++) b[i + head] = t[i];
}
const int S = N * 400;
int leftson[S], rightson[S], sum[S], cnt = 0, root[N];
/*
* Next, we'll use the idea of a tree array to construct a segment tree
* That is, the root[i] segment tree is responsible for information about some items in the a array
* For example, if there is a node in root[i] that is u and the interval that u is responsible for is l ~ r, then sum[u] records that
* a Some items in the array appear several times in l ~ r.
* So what exactly are the items of the a array? That's the idea of a tree array, where the item a[x] appears in the root[i] corresponding to the I determined in the following loop
* for(int i = x; i <= n ; i += lowbit(i))
* So if you want to know a[1], a[2],...A[x] How many of these 1 ~ x items are present in l ~ r, so you should look in these root[i] below
* for(int i = x; i > 0 ; i -= lowbit(i))
*/
int store[2][N], number[2];
/*
What does this store do, li k e now we're going to query the number of KTH places in a[left] ~ a[right]
Let's do it with a dichotomy, assuming we have [L, R], and we already know that there are so many res less than L in a[left] ~ a[right]
So we just want to see if mid = (L + R) > 1 can do the number k in a[left] ~ a[right], that's to find out a[left] ~ a[right]
How many of them are <= mid, because the k-th number in the rank must satisfy a[left] ~ a[right] where at least k are less than or equal to him, and he is the smallest number that meets this condition
The proof is very good. I won't write it.
So all we need to do is figure out how many of a[1] ~ a[left - 1] are <= mid, and then subtract from a[1] ~ a[right] how many are <= mid
Since we know there are so many res for < L in a[left] ~ a[right], we just need to find out how many of a[1] ~ a[left-1], a[1] ~ a[right] are in
[L, mid]This interval is fine, and then you find that what we need is a[1], a[2], a[3],...How many of a [left - 1] appear in L ~ mid, and the segment trees you need are the following
for(int i = left - 1; i > 0; i -= lowbit(i)),We determine that i exists in store[0] by this loop
Similarly, you need for (int I = right; I > 0; I - = lowbit (i)) to have the I determined by this loop in the store[1]
number[0]And number[1] is of course how many line segments are involved in storing the two loops separately
And we can combine the two-part process with the search process.
*/
void modify(int u, int l, int r, int x, int c) {
sum[u] += c;
if (l == r) return;
int mid = (l + r) >> 1;
if (x <= mid) {
if (leftson[u] == 0) leftson[u] = ++cnt;
modify(leftson[u], l, mid, x, c);
}
else {
if (rightson[u] == 0) rightson[u] = ++cnt;
modify(rightson[u], mid + 1, r, x, c);
}
}
// You will find that there is no need for pushup here, because this is a single modification, that is, there is more c in the x position of l ~ r.
int lowbit(int i) {
return i & -i;
}
void lookfortrees(int left, int right) {
number[0] = 0; number[1] = 0;
for (int i = left - 1; i > 0; i -= lowbit(i)) store[0][++number[0]] = root[i];
for (int i = right; i > 0; i -= lowbit(i)) store[1][++number[1]] = root[i];
}
void query(int L, int R, int pos) {
// Now we are using the dichotomy to find the answer to the pos operation, which of course means that the pos operation must be a query operation
if (L == R) { q[pos].ans = b[L]; return; }
// We guarantee that the root node of the segment tree now stored in the store is responsible for exactly L~R
int res = 0;
int mid = (L + R) >> 1;
for (int i = 1; i <= number[0]; i++) res -= sum[leftson[store[0][i]]];
for (int i = 1; i <= number[1]; i++) res += sum[leftson[store[1][i]]];
if (res >= q[pos].k) {
// If res >= q[pos]. K means you should go to the left
for (int i = 1; i <= number[0];i++) store[0][i] = leftson[store[0][i]];
for (int i = 1; i <= number[1]; i++) store[1][i] = leftson[store[1][i]];
query(L, mid, pos);
}
else {
q[pos].k -= res; // I don't want to explain this step anymore, just as part of the overall dichotomy template
for (int i = 1; i <= number[0]; i++) store[0][i] = rightson[store[0][i]];
for (int i = 1; i <= number[1]; i++) store[1][i] = rightson[store[1][i]];
query(mid + 1, R, pos);
}
// The above operation is really clever, making full use of the two partitions you are looking for, and the intervals responsible for the segment tree are in sync
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
b[++len] = a[i];
}
for (int i = 1; i <= m; i++) {
char op = 0; cin >> op;
if (op == 'Q') {
scanf("%d%d%d", &q[i].l, &q[i].r, &q[i].k);
q[i].kind = 1;
}
else {
scanf("%d%d", &q[i].x, &q[i].y);
b[++len] = q[i].y;
}
}
sort(b + 1, b + 1 + len);len = unique(b + 1, b + len + 1) - b - 1;
for (int x = 1; x <= n; x++) {
for (int i = x; i <= n; i += lowbit(i)) {
if (root[i] == 0) root[i] = ++cnt;
int p = lower_bound(b + 1, b + len + 1, a[x]) - b;
modify(root[i], 1, len, p, 1);
}
}
for (int i = 1; i <= m; i++) {
if (q[i].kind == 1) {
// This is a query operation
lookfortrees(q[i].l, q[i].r);
query(1, len, i);
printf("%d\n", q[i].ans);
}
else {
// Otherwise it is a modification operation
int x = q[i].x;
int p = lower_bound(b + 1, b + len + 1, a[x]) - b;
for (int i = x; i <= n; i += lowbit(i)) {
if (root[i] == 0) root[i] = ++cnt;
modify(root[i], 1, len, p, -1);
}
a[x] = q[i].y;
p = lower_bound(b + 1, b + len + 1, a[x]) - b;
for (int i = x; i <= n; i += lowbit(i)) {
if (root[i] == 0) root[i] = ++cnt;
modify(root[i], 1, len, p, 1);
}
}
}
}
2997.An inexperienced Librarian

// P3759 [TJOI2017] Undiligent Librarian
//2-D Segment Tree
#include<bits/stdc++.h>
#define Pli pair<ll,int>
#define mp make_pair
#define fir first
#define sec second
using namespace std;
typedef long long ll;
const ll sz=50050,N=sz*256,mod=1e9+7,RNK=51000;
void Plus(Pli &x,Pli y){x.fir+=y.fir;x.sec+=y.sec;}
/**************************Inner Segment Tree****************************/
//Weight Segment Tree, Book Priority is Weight
ll size[N];//Number of pages in a Book
int ch[N][2],cnt[N],tot;//Son Node, Number of Books, Dynamic Open Point Count
queue<int>rec;//Garbage collection
#define lson ch[k][0],l,mid
#define rson ch[k][1],mid+1,r
void destroy(int &k){size[k]=cnt[k]=ch[k][0]=ch[k][1]=0;rec.push(k);k=0;}
int newnode()
{
if (rec.empty()) return ++tot;
int ret=rec.front();
rec.pop();
return ret;
}
void add(int &k,int l,int r,int pos,ll x,int y)//Insert an x-page book at pos, a y-book, which can be negative
{
if (!k) k=newnode();
size[k]+=x;cnt[k]+=y;
size[k]=(size[k]+mod)%mod;
if (l==r)
{
if (!cnt[k]) destroy(k);
return;
}
int mid=(l+r)>>1;
if (pos<=mid) add(lson,pos,x,y);
else add(rson,pos,x,y);
if (!cnt[k]) destroy(k);
}
Pli Query(int k,int l,int r,int x,int y)//Number of pages and books in x~y interval
{
if (!k) return mp(0ll,0ll);
if (x<=l&&r<=y) return mp(size[k],cnt[k]);
int mid=(l+r)>>1;
Pli ret;
ret.fir=0ll;ret.sec=0;
if (x<=mid) Plus(ret,Query(lson,x,y));
if (y>mid) Plus(ret,Query(rson,x,y));
return ret;
}
#undef lson
#undef rson
/*************************Outer Segment Tree*****************************************/
#define lson k<<1,l,mid
#define rson k<<1|1,mid+1,r
int root[N];
void insert(int k,int l,int r,int pos,int x,int sum)
{
add(root[k],1,RNK,x,sum,1);
if (l==r) return;
int mid=(l+r)>>1;
if (pos<=mid) insert(lson,pos,x,sum);
else insert(rson,pos,x,sum);
}
void del(int k,int l,int r,int pos,int x,int sum)
{
add(root[k],1,RNK,x,-sum,-1);//Negative number, delete
if (l==r) return;
int mid=(l+r)>>1;
if (pos<=mid) del(lson,pos,x,sum);
else del(rson,pos,x,sum);
}
Pli Ask(int k,int l,int r,int x,int y,int L,int R)
//Number of pages and books of L~R (weight interval) in x~y
{
if (x<=l&&r<=y) return Query(root[k],1,RNK,L,R);
int mid=(l+r)>>1;
Pli ret;
ret.fir=0ll;ret.sec=0;
if (x<=mid) Plus(ret,Ask(lson,x,y,L,R));
if (y>mid) Plus(ret,Ask(rson,x,y,L,R));
ret.fir%=mod;
return ret;
}
#undef lson
#undef rson
/************************************************************/
int a[sz],n,m;
ll sum[sz],ans;
//a[i] i Priority of books on location
//Number of pages of a book in sum[i] i position
ll read()
{
register ll ret=0;
register char ch=getchar();
while (ch>'9'||ch<'0') ch=getchar();
while (ch<='9'&&ch>='0') ret=(ret<<1)+(ret<<3)+(ch^48),ch=getchar();
return ret;
}
int main()
{
register int i,x,y;
n=read();m=read();
for (i=1;i<=n;i++) a[i]=read(),sum[i]=read()%mod;
for (i=1;i<=n;i++) insert(1,1,n,i,a[i],sum[i]);
for (i=1;i<=n;i++)
{
Pli cur=Ask(1,1,n,i+1,n,1,a[i]);
ans+=sum[i]*cur.sec+cur.fir;
ans%=mod;
}
while(m--)
{
x=read(),y=read();
if(x>y) swap(x,y);
if(x==y){printf("%lld\n",ans);continue;}//No exchange
int L=a[x],R=a[y],cnt,mn=min(L,R),mx=max(L,R);
ll size;
Pli cur;
//Books with weights greater than mn and less than mx in x~y contribute
cur=Ask(1,1,n,x,y,mn+1,mx-1);
size=cur.fir,cnt=cur.sec;
ans+=(mn==L?1:-1)*(2*size%mod+(ll)(cnt+1)*(sum[x]+sum[y])%mod)%mod;
ans%=mod;
//Books with weights less than mn in x~y contribute
cur=Ask(1,1,n,x,y,1,mn-1);
cnt=cur.sec;
(ans+=(ll)cnt*(sum[y]-sum[x])%mod)%=mod;
//Books with weights greater than mx in x~y contribute
cur=Ask(1,1,n,x,y,mx+1,n);
cnt=cur.sec;
(ans+=(ll)cnt*(sum[x]-sum[y])%mod)%=mod;
if(ans<0) ans+=mod;
del(1,1,n,x,a[x],sum[x]);del(1,1,n,y,a[y],sum[y]);//Delete the original
insert(1,1,n,x,a[y],sum[y]);insert(1,1,n,y,a[x],sum[x]);//Add New
swap(a[x],a[y]);swap(sum[x],sum[y]);//change
printf("%lld\n",ans);
}
}
Blocking is good if you don't want to write or don't want to write data structures. Then there are two ways to write, one is to sort each block, the other is to maintain a tree array for each block.
In this way, L and R are in the same block, the two incomplete blocks where L and R are located, and the complete blocks that L and R cross are discussed in three cases.
Note!! The first two situations in this question must not be violent rebuilding blocks! Violent rebuilding takes 1200+s, only 80+s if only the changed parts are updated.
Another problem is that because the complexity of the block marker is O(nSlogn), where S is the size of the block, S is set to nlogn__twice as fast as n_.
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
typedef long long ll;
#define rep(i,l,r) for (register int i=l; i<=r; i++)
using namespace std;
const ll N=50100,md=1000000007;
int n,m,mx,L,R,B,a[N],v[N],sz[N],bl[N],cnt,sum[N],d[300],c[250][N],c1[250][N],ans;
void add(int c[],int x,int k){ for (; x<=n; x+=x&-x) c[x]=(c[x]+k)%md; }
int que(int c[],int x){ ll res=0; for (; x; x-=x&-x) res=(res+c[x])%md; return res; }
void add1(int c1[],int x,int k){ for (; x<=n; x+=x&-x) c1[x]=(c1[x]+k)%md; }
int que1(int c1[],int x){ ll res=0; for (; x; x-=x&-x) res=(res+c1[x])%md; return res; }
int get(int x){ return x>=0 ? x : x+md; }
void cal(int x,int y,int z){
if (a[x]<a[z]) ans=(ans+v[x]+v[z])%md; else ans=(ans-v[x]-v[z]+md+md)%md;
if (a[y]<a[z]) ans=(ans+md+md-v[y]-v[z])%md; else ans=(ans+v[y]+v[z])%md;
}
void work(int L,int R){
if (L==R) return;
if (bl[L]==bl[R]){
rep(i,L+1,R-1) cal(L,R,i); swap(a[L],a[R]); swap(v[L],v[R]);
}else{
rep(i,L+1,(bl[L]-1)*B+sz[bl[L]]) cal(L,R,i);
rep(i,(bl[R]-1)*B+1,R-1) cal(L,R,i);
swap(a[L],a[R]); swap(v[L],v[R]);
sum[bl[L]]=(sum[bl[L]]+md-v[R]+v[L])%md; sum[bl[R]]=(sum[bl[R]]+md-v[L]+v[R])%md;
add(c[bl[R]],a[L],-v[L]); add(c[bl[L]],a[R],-v[R]); add1(c1[bl[R]],a[L],-1); add1(c1[bl[L]],a[R],-1);
add(c[bl[L]],a[L],v[L]); add(c[bl[R]],a[R],v[R]); add1(c1[bl[L]],a[L],1); add1(c1[bl[R]],a[R],1);
rep(i,bl[L]+1,bl[R]-1){
ans=get((1ll*ans-(que(c[i],a[R]-1)+1ll*que1(c1[i],a[R]-1)*v[R])%md));
ans=get((1ll*ans+(que(c[i],a[L]-1)+1ll*que1(c1[i],a[L]-1)*v[L]))%md);
ans=get((1ll*ans-(sum[i]-que(c[i],a[L])+1ll*(sz[i]-que1(c1[i],a[L]))*v[L]))%md);
ans=get((1ll*ans+(sum[i]-que(c[i],a[R])+1ll*(sz[i]-que1(c1[i],a[R]))*v[R]))%md);
}
}
if (a[R]<a[L]) ans=(1ll*ans+v[L]+v[R])%md; else ans=get((1ll*ans-(v[L]+v[R]))%md);
}
int main(){
freopen("book.in","r",stdin);
freopen("book.out","w",stdout);
scanf("%d%d",&n,&m); B=(int)sqrt(n*17);
rep(i,1,n) scanf("%d%d",&a[i],&v[i]);
rep(i,1,n) bl[i]=(i-1)/B+1; mx=(n-1)/B+1;
rep(i,1,mx-1) sz[i]=B; sz[mx]=n-(mx-1)*B;
rep(i,1,n) add(c[bl[i]],a[i],v[i]),add1(c1[bl[i]],a[i],1),sum[bl[i]]=(sum[bl[i]]+v[i])%md;
rep(i,1,n){
ans=get((1ll*ans+(i-1-1ll*que1(c1[0],a[i]-1))*v[i]+cnt-que(c[0],a[i]-1))%md);
add(c[0],a[i],v[i]); add1(c1[0],a[i],1); cnt=(cnt+v[i])%md;
}
rep(i,1,m) scanf("%d%d",&L,&R),work(min(L,R),max(L,R)),printf("%d\n",ans);
return 0;
}
The basic idea of partitioning
AcWing 243.A simple integer problem 2
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
typedef long long LL;
const int N = 100010, M = 350;
int n, m, len;
LL add[M], sum[M];
int w[N];
int get(int i)
{
return i / len;
}
void change(int l, int r, int d)
{
if (get(l) == get(r)) // Direct Violence in Segments
{
for (int i = l; i <= r; i ++ ) w[i] += d, sum[get(i)] += d;
}
else
{
int i = l, j = r;
while (get(i) == get(l)) w[i] += d, sum[get(i)] += d, i ++ ;
while (get(j) == get(r)) w[j] += d, sum[get(j)] += d, j -- ;
for (int k = get(i); k <= get(j); k ++ ) sum[k] += len * d, add[k] += d;
}
}
LL query(int l, int r)
{
LL res = 0;
if (get(l) == get(r)) // Direct Violence in Segments
{
for (int i = l; i <= r; i ++ ) res += w[i] + add[get(i)];
}
else
{
int i = l, j = r;
while (get(i) == get(l)) res += w[i] + add[get(i)], i ++ ;
while (get(j) == get(r)) res += w[j] + add[get(j)], j -- ;
for (int k = get(i); k <= get(j); k ++ ) res += sum[k];
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
len = sqrt(n);
for (int i = 1; i <= n; i ++ )
{
scanf("%d", &w[i]);
sum[get(i)] += w[i];
}
char op[2];
int l, r, d;
while (m -- )
{
scanf("%s%d%d", op, &l, &r);
if (*op == 'C')
{
scanf("%d", &d);
change(l, r, d);
}
else printf("%lld\n", query(l, r));
}
return 0;
}
Blocked Chain List
AcWing 947.text editor
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2000, M = 2010;
int n, x, y;
struct Node
{
char s[N + 1];
int c, l, r;
}p[M];
char str[2000010];
int q[M], tt; // Memory Recycling
void move(int k) // Move after the first k characters
{
x = p[0].r;
while (k > p[x].c) k -= p[x].c, x = p[x].r;
y = k - 1;
}
void add(int x, int u) // Insert node u to the right of node x
{
p[u].r = p[x].r, p[p[u].r].l = u;
p[x].r = u, p[u].l = x;
}
void del(int u) // Delete Node u
{
p[p[u].l].r = p[u].r;
p[p[u].r].l = p[u].l;
p[u].l = p[u].r = p[u].c = 0; // Empty Node u
q[ ++ tt] = u; // Recycle Node u
}
void insert(int k) // Insert k characters after cursor
{
if (y < p[x].c - 1) // Split from cursor
{
int u = q[tt -- ]; // Create a new node
for (int i = y + 1; i < p[x].c; i ++ )
p[u].s[p[u].c ++ ] = p[x].s[i];
p[x].c = y + 1;
add(x, u);
}
int cur = x;
for (int i = 0; i < k;)
{
int u = q[tt -- ]; // Create a new block
while (p[u].c < N && i < k)
p[u].s[p[u].c ++ ] = str[i ++ ];
add(cur, u);
cur = u;
}
}
void remove(int k) // Delete k characters after cursor
{
if (p[x].c - 1 - y >= k) // Delete within node
{
for (int i = y + k + 1, j = y + 1; i < p[x].c; i ++, j ++ ) p[x].s[j] = p[x].s[i];
p[x].c -= k;
}
else
{
k -= p[x].c - y - 1; // Delete the remainder of the current node
p[x].c = y + 1;
while (p[x].r && k >= p[p[x].r].c)
{
int u = p[x].r;
k -= p[u].c;
del(u);
}
int u = p[x].r; // Delete the first half of the end node
for (int i = 0, j = k; j < p[u].c; i ++, j ++ ) p[u].s[i] = p[u].s[j];
p[u].c -= k;
}
}
void get(int k) // Returns k characters from the cursor
{
if (p[x].c - 1 - y >= k) // Return within node
{
for (int i = 0, j = y + 1; i < k; i ++, j ++ ) putchar(p[x].s[j]);
}
else
{
k -= p[x].c - y - 1;
for (int i = y + 1; i < p[x].c; i ++ ) putchar(p[x].s[i]); // Output the remainder of the current node
int cur = x;
while (p[cur].r && k >= p[p[cur].r].c)
{
int u = p[cur].r;
for (int i = 0; i < p[u].c; i ++ ) putchar(p[u].s[i]);
k -= p[u].c;
cur = u;
}
int u = p[cur].r;
for (int i = 0; i < k; i ++ ) putchar(p[u].s[i]);
}
puts("");
}
void prev() // Move the cursor one place forward
{
if (!y)
{
x = p[x].l;
y = p[x].c - 1;
}
else y -- ;
}
void next() // Move the cursor one bit backward
{
if (y < p[x].c - 1) y ++ ;
else
{
x = p[x].r;
y = 0;
}
}
void merge() // Core of block chain table time complexity by merging short neighboring nodes
{
for (int i = p[0].r; i; i = p[i].r)
{
while (p[i].r && p[i].c + p[p[i].r].c < N)
{
int r = p[i].r;
for (int j = p[i].c, k = 0; k < p[r].c; j ++, k ++ )
p[i].s[j] = p[r].s[k];
if (x == r) x = i, y += p[i].c; // Update cursor position
p[i].c += p[r].c;
del(r);
}
}
}
int main()
{
for (int i = 1; i < M; i ++ ) q[ ++ tt] = i;
scanf("%d", &n);
char op[10];
str[0] = '>';
insert(1); // Insert Sentry
move(1); // Move the cursor behind the sentry
while (n -- )
{
int a;
scanf("%s", op);
if (!strcmp(op, "Move"))
{
scanf("%d", &a);
move(a + 1);
}
else if (!strcmp(op, "Insert"))
{
scanf("%d", &a);
int i = 0, k = a;
while (a)
{
str[i] = getchar();
if (str[i] >= 32 && str[i] <= 126) i ++, a -- ;
}
insert(k);
merge();
}
else if (!strcmp(op, "Delete"))
{
scanf("%d", &a);
remove(a);
merge();
}
else if (!strcmp(op, "Get"))
{
scanf("%d", &a);
get(a);
}
else if (!strcmp(op, "Prev")) prev();
else next();
}
return 0;
}
The Foundation of Moche Team
AcWing 2492.HH Necklace
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 50010, M = 200010, S = 1000010;
int n, m, len;
int w[N], ans[M];
struct Query
{
int id, l, r;
}q[M];
int cnt[S];
int get(int x)
{
return x / len;
}
bool cmp(const Query& a, const Query& b)
{
int i = get(a.l), j = get(b.l);
if (i != j) return i < j;
return a.r < b.r;
}
void add(int x, int& res)
{
if (!cnt[x]) res ++ ;
cnt[x] ++ ;
}
void del(int x, int& res)
{
cnt[x] -- ;
if (!cnt[x]) res -- ;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
scanf("%d", &m);
len = max(1, (int)sqrt((double)n * n / m));
for (int i = 0; i < m; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
q[i] = {i, l, r};
}
sort(q, q + m, cmp);
for (int k = 0, i = 0, j = 1, res = 0; k < m; k ++ )
{
int id = q[k].id, l = q[k].l, r = q[k].r;
while (i < r) add(w[ ++ i], res);
while (i > r) del(w[i -- ], res);
while (j < l) del(w[j ++ ], res);
while (j > l) add(w[ -- j], res);
ans[id] = res;
}
for (int i = 0; i < m; i ++ ) printf("%d\n", ans[i]);
return 0;
}
Moche Team with Modified Moche Team
AcWing 2521.Number color
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 10010, S = 1000010;
int n, m, mq, mc, len;
int w[N], cnt[S], ans[N];
struct Query
{
int id, l, r, t;
}q[N];
struct Modify
{
int p, c;
}c[N];
int get(int x)
{
return x / len;
}
bool cmp(const Query& a, const Query& b)
{
int al = get(a.l), ar = get(a.r);
int bl = get(b.l), br = get(b.r);
if (al != bl) return al < bl;
if (ar != br) return ar < br;
return a.t < b.t;
}
void add(int x, int& res)
{
if (!cnt[x]) res ++ ;
cnt[x] ++ ;
}
void del(int x, int& res)
{
cnt[x] -- ;
if (!cnt[x]) res -- ;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
for (int i = 0; i < m; i ++ )
{
char op[2];
int a, b;
scanf("%s%d%d", op, &a, &b);
if (*op == 'Q') mq ++, q[mq] = {mq, a, b, mc};
else c[ ++ mc] = {a, b};
}
len = cbrt((double)n * mc) + 1;
sort(q + 1, q + mq + 1, cmp);
for (int i = 0, j = 1, t = 0, k = 1, res = 0; k <= mq; k ++ )
{
int id = q[k].id, l = q[k].l, r = q[k].r, tm = q[k].t;
while (i < r) add(w[ ++ i], res);
while (i > r) del(w[i -- ], res);
while (j < l) del(w[j ++ ], res);
while (j > l) add(w[ -- j], res);
while (t < tm)
{
t ++ ;
if (c[t].p >= j && c[t].p <= i)
{
del(w[c[t].p], res);
add(c[t].c, res);
}
swap(w[c[t].p], c[t].c);
}
while (t > tm)
{
if (c[t].p >= j && c[t].p <= i)
{
del(w[c[t].p], res);
add(c[t].c, res);
}
swap(w[c[t].p], c[t].c);
t -- ;
}
ans[id] = res;
}
for (int i = 1; i <= mq; i ++ ) printf("%d\n", ans[i]);
return 0;
}
Moche team roll back Moche team
AcWing 2523.Historical Studies

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, m, len;
int w[N], cnt[N];
LL ans[N];
struct Query
{
int id, l, r;
}q[N];
vector<int> nums;
int get(int x)
{
return x / len;
}
bool cmp(const Query& a, const Query& b)
{
int i = get(a.l), j = get(b.l);
if (i != j) return i < j;
return a.r < b.r;
}
void add(int x, LL& res)
{
cnt[x] ++ ;
res = max(res, (LL)cnt[x] * nums[x]);
}
int main()
{
scanf("%d%d", &n, &m);
len = sqrt(n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]), nums.push_back(w[i]);
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
for (int i = 1; i <= n; i ++ )
w[i] = lower_bound(nums.begin(), nums.end(), w[i]) - nums.begin();
for (int i = 0; i < m; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
q[i] = {i, l, r};
}
sort(q, q + m, cmp);
for (int x = 0; x < m;)
{
int y = x;
while (y < m && get(q[y].l) == get(q[x].l)) y ++ ;
int right = get(q[x].l) * len + len - 1;
// Violent inquiry within block
while (x < y && q[x].r <= right)
{
LL res = 0;
int id = q[x].id, l = q[x].l, r = q[x].r;
for (int k = l; k <= r; k ++ ) add(w[k], res);
ans[id] = res;
for (int k = l; k <= r; k ++ ) cnt[w[k]] -- ;
x ++ ;
}
// Ask outside block
LL res = 0;
int i = right, j = right + 1;
while (x < y)
{
int id = q[x].id, l = q[x].l, r = q[x].r;
while (i < r) add(w[ ++ i], res);
LL backup = res;
while (j > l) add(w[ -- j], res);
ans[id] = res;
while (j < right + 1) cnt[w[j ++ ]] -- ;
res = backup;
x ++ ;
}
memset(cnt, 0, sizeof cnt);
}
for (int i = 0; i < m; i ++ ) printf("%lld\n", ans[i]);
return 0;
}
Tree of Moquorum
AcWing 2534.Tree Count 2
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
const int N = 100010;
int n, m, len;
int w[N];
int h[N], e[N], ne[N], idx;
int depth[N], f[N][16];
int seq[N], top, first[N], last[N];
int cnt[N], st[N], ans[N];
int que[N];
struct Query
{
int id, l, r, p;
}q[N];
vector<int> nums;
void add_edge(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int father)
{
seq[ ++ top] = u;
first[u] = top;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j != father) dfs(j, u);
}
seq[ ++ top] = u;
last[u] = top;
}
void bfs()
{
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[1] = 1;
int hh = 0, tt = 0;
que[0] = 1;
while (hh <= tt)
{
int t = que[hh ++ ];
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (depth[j] > depth[t] + 1)
{
depth[j] = depth[t] + 1;
f[j][0] = t;
for (int k = 1; k <= 15; k ++ )
f[j][k] = f[f[j][k - 1]][k - 1];
que[ ++ tt] = j;
}
}
}
}
int lca(int a, int b)
{
if (depth[a] < depth[b]) swap(a, b);
for (int k = 15; k >= 0; k -- )
if (depth[f[a][k]] >= depth[b])
a = f[a][k];
if (a == b) return a;
for (int k = 15; k >= 0; k -- )
if (f[a][k] != f[b][k])
{
a = f[a][k];
b = f[b][k];
}
return f[a][0];
}
int get(int x)
{
return x / len;
}
bool cmp(const Query& a, const Query& b)
{
int i = get(a.l), j = get(b.l);
if (i != j) return i < j;
return a.r < b.r;
}
void add(int x, int& res)
{
st[x] ^= 1;
if (st[x] == 0)
{
cnt[w[x]] -- ;
if (!cnt[w[x]]) res -- ;
}
else
{
if (!cnt[w[x]]) res ++ ;
cnt[w[x]] ++ ;
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]), nums.push_back(w[i]);
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
for (int i = 1; i <= n; i ++ )
w[i] = lower_bound(nums.begin(), nums.end(), w[i]) - nums.begin();
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add_edge(a, b), add_edge(b, a);
}
dfs(1, -1);
bfs();
for (int i = 0; i < m; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
if (first[a] > first[b]) swap(a, b);
int p = lca(a, b);
if (a == p) q[i] = {i, first[a], first[b]};
else q[i] = {i, last[a], first[b], p};
}
len = sqrt(top);
sort(q, q + m, cmp);
for (int i = 0, L = 1, R = 0, res = 0; i < m; i ++ )
{
int id = q[i].id, l = q[i].l, r = q[i].r, p = q[i].p;
while (R < r) add(seq[ ++ R], res);
while (R > r) add(seq[R -- ], res);
while (L < l) add(seq[L ++ ], res);
while (L > l) add(seq[ -- L], res);
if (p) add(p, res);
ans[id] = res;
if (p) add(p, res);
}
for (int i = 0; i < m; i ++ ) printf("%d\n", ans[i]);
return 0;
}
MO Team's Second Offline Mo Team
AcWing 2535.Second Offline Mouse Team

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 500010, M = 5000007, INF = 0x3f3f3f3f;
int read()
{
int x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}
return x * f;
}
int n, m;
int block, k;
int w[N];
ll ans[N];
struct Query
{
int id, l, r;
ll res;
}q[N];
struct Range
{
int id, l, r, t;//t denotes type+/-
};
vector<Range>range[N];
int f[N], g[N];
//How many 1's are there under the binary of x
inline int get_count(int x)
{
int res = 0;
while(x)res += x & 1, x >>= 1;
return res;
}
inline int get_block(int x)
{
return x / block;
}
bool cmp(const Query& a, const Query& b)
{
int x = get_block(a.l);
int y = get_block(b.l);
if(x != y)return x < y;
return a.r < b.r;
}
int main()
{
n = read(), m = read(), k = read();
for(int i = 1; i <= n; ++ i)
w[i] = read();
vector<int> nums;
//Preprocess all binary numbers in a given range to k
for(int i = 0; i < (1 << 14); ++ i){
if(get_count(i) == k)
nums.push_back(i);
}
for(int i = 1; i <= n; ++ i){
//g[i] is a bucket indicating how many of the first I pair with x
for(auto it : nums) ++ g[w[i] ^ it];
//f[i] indicates how many pairs of wi+1 exist in w1 ~ wi
f[i] = g[w[i + 1]];
}
for(int i = 0; i < m; ++ i){
int l = read(), r = read();
q[i] = {i, l, r};
}
block = sqrt(n);
sort(q, q + m, cmp);
for(int i = 0, L = 1, R = 0; i < m; ++ i){
int l = q[i].l, r = q[i].r, id = q[i].id;
if(R < r) range[L - 1].push_back({i, R + 1, r, -1});
while(R < r) q[i].res += f[R ++ ];
if(R > r) range[L - 1].push_back({i, r + 1, R, 1});
while(R > r) q[i].res -= f[ -- R];//S(R) = f(R - 1)
if(L < l) range[R].push_back({i, L, l - 1, -1});
while(L < l) q[i].res += f[L - 1] + (k == 0), L ++ ;
if(L > l) range[R].push_back({i, l, L - 1, 1});
while(L > l) q[i].res -= f[L - 2] + (k == 0), L -- ;
}
memset(g, 0, sizeof g);
for(int i = 1; i <= n; ++ i){
for(auto it : nums) ++ g[w[i] ^it];
for(auto it : range[i]){
int id = it.id, l = it.l, r = it.r, t = it.t;
for(int x = l; x <= r; ++ x)
q[id].res += g[w[x]] * t;
}
}
for(int i = 1; i < m; ++ i) q[i].res += q[i - 1].res;
for(int i = 0; i < m; ++ i) ans[q[i].id] = q[i].res;
for(int i = 0; i < m; ++ i) printf("%lld\n", ans[i]);
return 0;
}
Author: Fan Fanさん
Links: https://www.acwing.com/solution/content/26293/
Source: AcWing
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.
Tree Chain Split
AcWing 2568.Tree Chain Split
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, M = N << 1;
int n, m;
int h[N], w[N], e[M], ne[M], idx; //Build Trees
int id[N], nw[N], cnt; //Id: The dfn sequence number of the node, nw[id[i]] is the weight w of I (mapping of w -> nw)
int dep[N], sz[N], top[N], fa[N], son[N];
//sz: Number of subtree nodes, top: Vertex of heavy chain, son: Heavy son, fa: Parent node
struct SegmentTree
{
int l, r;
LL sum, flag;
}tr[N << 2];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
//dfs1 preprocessing
void dfs1(int u, int father, int depth)
{
dep[u] = depth, fa[u] = father, sz[u] = 1;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == father) continue;
dfs1(j, u, depth + 1);
sz[u] += sz[j];
if (sz[son[u]] < sz[j]) son[u] = j; //The second son is the son with the most subtree nodes
}
}
//dfs2 is split (t is the vertex of the heavy chain)
void dfs2(int u, int t)
{
id[u] = ++ cnt, nw[cnt] = w[u], top[u] = t;
if (!son[u]) return; //End of leaf node
dfs2(son[u], t); //Heavy Chain Splitting for Heavy Sons
//Handle your younger son
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa[u] || j == son[u]) continue;
dfs2(j, j); //The pinnacle of the light son's heavy chain is himself
}
}
//--------------------------------------------------------------------------------\
void pushup(int u)
{
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
if (root.flag)
{
left.sum += root.flag * (left.r - left.l + 1);
left.flag += root.flag;
right.sum += root.flag * (right.r - right.l + 1);
right.flag += root.flag;
root.flag = 0;
}
}
void build(int u, int l, int r)
{
tr[u] = {l, r, nw[r], 0};
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
void update(int u, int l, int r, int k)
{
if (l <= tr[u].l && r >= tr[u].r)
{
tr[u].flag += k;
tr[u].sum += k * (tr[u].r - tr[u].l + 1);
return;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) update(u << 1, l, r, k);
if (r > mid) update(u << 1 | 1, l, r, k);
pushup(u);
}
LL query(int u, int l, int r)
{
if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum;
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
LL res = 0;
if (l <= mid) res += query(u << 1, l, r);
if (r > mid) res += query(u << 1 | 1, l, r);
return res;
}
//--------------------------------------------------------------------------------\
void update_path(int u, int v, int k)
{
while (top[u] != top[v]) //Climb up to find the same heavy chain
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
update(1, id[top[u]], id[u], k); //dfs order reason, the id of the node above must be less than the id of the node below
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
update(1, id[v], id[u], k); //In the same heavy chain, process the remaining intervals
}
LL query_path(int u, int v)
{
LL res = 0;
while (top[u] != top[v]) //Climb up to find the same heavy chain
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
res += query(1, id[top[u]], id[u]);
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
res += query(1, id[v], id[u]); //In the same heavy chain, process the remaining intervals
return res;
}
void update_tree(int u, int k) //Subtree plus k
{
update(1, id[u], id[u] + sz[u] - 1, k); //Because of dfs order, intervals can be found directly by using the number of subtree nodes
}
LL query_tree(int u)
{
return query(1, id[u], id[u] + sz[u] - 1); //For the same reason
}
int main()
{
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
for (int i = 1; i < n; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
dfs1(1, -1, 1);
dfs2(1, 1);
build(1, 1, n);
scanf("%d", &m);
while (m -- )
{
int t, u, v, k;
scanf("%d%d", &t, &u);
if (t == 1)
{
scanf("%d%d", &v, &k);
update_path(u, v, k);
}
else if (t == 2)
{
scanf("%d", &k);
update_tree(u, k);
}
else if (t == 3)
{
scanf("%d", &v);
printf("%lld\n", query_path(u, v));
}
else printf("%lld\n", query_tree(u));
}
return 0;
}
Author: Colored Pencil
Links: https://www.acwing.com/solution/content/62664/
Source: AcWing
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.
2524.Tree Chain Split II (Root-changing Tree Chain Split)

#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, M = N << 1;
int n, m;
int h[N], e[M], ne[M], w[M], idx;
int id[N], nw[N], cnt;
int dep[N], sz[N], top[N], fa[N], son[N];
int root;
struct SegmentTree
{
int l, r;
LL sum, flag;
}tr[N << 2];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs1(int u, int father, int depth)
{
dep[u] = depth, fa[u] = father, sz[u] = 1;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == father) continue;
dfs1(j, u, depth + 1);
sz[u] += sz[j];
if (sz[son[u]] < sz[j]) son[u] = j;
}
}
void dfs2(int u, int t)
{
id[u] = ++ cnt, nw[cnt] = w[u], top[u] = t;
if (!son[u]) return;
dfs2(son[u], t);
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa[u] || j == son[u]) continue;
dfs2(j, j);
}
}
//--------------------------------------------------------------------------------\
void pushup(int u)
{
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
if (root.flag)
{
left.sum += root.flag * (left.r - left.l + 1);
left.flag += root.flag;
right.sum += root.flag * (right.r - right.l + 1);
right.flag += root.flag;
root.flag = 0;
}
}
void build(int u, int l, int r)
{
tr[u] = {l, r, nw[r], 0};
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
void update(int u, int l, int r, int k)
{
if (l <= tr[u].l && r >= tr[u].r)
{
tr[u].flag += k;
tr[u].sum += k * (tr[u].r - tr[u].l + 1);
return;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) update(u << 1, l, r, k);
if (r > mid) update(u << 1 | 1, l, r, k);
pushup(u);
}
LL query(int u, int l, int r)
{
if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum;
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
LL res = 0;
if (l <= mid) res += query(u << 1, l, r);
if (r > mid) res += query(u << 1 | 1, l, r);
return res;
}
//--------------------------------------------------------------------------------\
int lca(int u, int v)
{
while (top[u] != top[v])
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
u = fa[top[u]];
}
if (dep[u] > dep[v]) swap(u, v);
return u;
}
void update_path(int u, int v, int k)
{
while (top[u] != top[v])
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
update(1, id[top[u]], id[u], k);
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
update(1, id[v], id[u], k);
}
LL query_path(int u, int v)
{
LL res = 0;
while (top[u] != top[v])
{
if (dep[top[u]] < dep[top[v]]) swap(u, v);
res += query(1, id[top[u]], id[u]);
u = fa[top[u]];
}
if (dep[u] < dep[v]) swap(u, v);
res += query(1, id[v], id[u]);
return res;
}
void update_tree(int u, int k)
{
if (u == root) update(1, 1, n, k);
else if (lca(u, root) == u)
{
update(1, 1, n, k);
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (lca(j, root) == j)
{
update(1, id[j], id[j] + sz[j] - 1, -k);
break;
}
}
}
else update(1, id[u], id[u] + sz[u] - 1, k);
}
LL query_tree(int u)
{
if (u == root) return query(1, 1, n);
else if (lca(u, root) == u)
{
LL res = query(1, 1, n);
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (lca(j, root) == j)
{
res -= query(1, id[j], id[j] + sz[j] - 1);
return res;
}
}
}
else return query(1, id[u], id[u] + sz[u] - 1);
}
int main()
{
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
for (int i = 2; i <= n; i ++ )
{
int a;
scanf("%d", &a);
add(a, i);
}
dfs1(1, -1, 1);
dfs2(1, 1);
build(1, 1, n);
scanf("%d", &m);
while (m -- )
{
int t, u, v, k;
scanf("%d%d", &t, &u);
if (t == 1) root = u;
else if (t == 2)
{
scanf("%d%d", &v, &k);
update_path(u, v, k);
}
else if (t == 3)
{
scanf("%d", &k);
update_tree(u, k);
}
else if (t == 4)
{
scanf("%d", &v);
printf("%lld\n", query_path(u, v));
}
else printf("%lld\n", query_tree(u));
}
return 0;
}
AcWing 918. Package Manager


Lightweight Chain Split
It is not difficult to see that this dependency is a tree rooted at point 00.
Each operation on a node numbered xx
Installation requires that all points from the root node to the xx path be set to 11
The uninstall operation requires that all points in the subtree rooted in xx be set to 00
Analysis that seems to have no value
Each operation requires the number of packages whose state has been changed, so maintain the sum of installed packages in the segment tree.
Interval assignments are also lazy to mark pushdown.
See code for details.
Time Complexity O(mlog2n)
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100010, M = N << 1;
int h[N], e[N], ne[N], idx;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int n, m;
int dep[N], f[N], sz[N], son[N];
void dfs(int u, int fa)
{
dep[u] = dep[fa] + 1, f[u] = fa, sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
dfs(j, u);
sz[u] += sz[j];
if(sz[j] > sz[son[u]]) son[u] = j;
}
}
int id[N], rk[N], top[N], tot;
void dfs2(int u, int t)
{
id[u] = ++ tot, rk[tot] = u, top[u] = t;
if(son[u]) dfs2(son[u], t);
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(son[u] == j) continue;
dfs2(j, j);
}
}
struct Node{
int l, r;
int sum, lazy;
}tr[N << 2];
void build(int u, int l, int r)
{
tr[u] = {l, r};
if(l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void pushup(int u)
{
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
if(tr[u].lazy)
{
Node &left = tr[u << 1], &right = tr[u << 1 | 1];
if(tr[u].lazy == 1)
{
left.sum = left.r - left.l + 1;
right.sum = right.r - right.l + 1;
}
else
left.sum = right.sum = 0;
left.lazy = right.lazy = tr[u].lazy;
tr[u].lazy = 0;
}
}
// Typee is 1 interval coverage, type is 2 interval deletion
void modify(int u, int l, int r, int type)
{
if(tr[u].l >= l and tr[u].r <= r)
{
if(type == 1)
{
tr[u].sum = tr[u].r - tr[u].l + 1;
tr[u].lazy = 1;
}
else
{
tr[u].sum = 0;
tr[u].lazy = 2;
}
return;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u << 1, l, r, type);
if(r > mid) modify(u << 1 | 1, l, r, type);
pushup(u);
}
int query(int u, int l, int r)
{
if(tr[u].l >= l and tr[u].r <= r) return tr[u].sum;
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1, res = 0;
if(l <= mid) res = query(u << 1, l, r);
if(r > mid) res += query(u << 1 | 1, l, r);
return res;
}
// Set the root node to all points on the x-path to 1
int install(int x)
{
int res = 0;
while(x)
{
res += (id[x] - id[top[x]] + 1) - query(1, id[top[x]], id[x]);
modify(1, id[top[x]], id[x], 1);
x = f[top[x]];
}
return res;
}
// Set all points in the subtree rooted in x to zero
int uninstall(int x)
{
int res = query(1, id[x], id[x] + sz[x] - 1);
modify(1, id[x], id[x] + sz[x] - 1, 2);
x = f[top[x]];
return res;
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d", &n);
for(int i = 2; i <= n; i ++)
{
int x;
scanf("%d", &x);
x ++;
add(x, i);
}
dfs(1, 0);
dfs2(1, 1);
build(1, 1, n);
scanf("%d", &m);
while(m --)
{
char op[10];
int x;
scanf("%s%d", op, &x);
x ++;
if(op[0] == 'i') printf("%d\n", install(x));
else printf("%d\n", uninstall(x));
}
return 0;
}
Author: Funny_ωノ
Links: https://www.acwing.com/solution/content/21661/
Source: AcWing
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.
Dynamic Tree
Link - Cut Tree
LCT is a data structure for solving dynamic tree problems
Dynamic Tree Problem:
Maintain a forest, support deleting an edge, add an edge, and make sure to add an edge, even after deletion!! Forest!!. We want to maintain some information about the forest.
General operations have two points of connectivity, two-point path weights, connecting two points and cutting an edge, modifying information, and so on
He is somewhat similar to tree splitting, which is done by dividing by subtree size and then dynamically maintaining the lognlog_n intervals split
LCT uses multiple Splays to maintain multiple real chains, and Splay's characteristics allow us to merge and split trees.
The benefits of LCT are:
LCT s that Tree-chain splitting can do are basically able to do
The time complexity of a tree chain split processing query is O(log2 n)O(log2_n), while LCTLCT is O(log n)O(log_n)
Note, however, that the LCTLCT constant is very large (as can be seen from its complexity)
So you can add macro definitions and convergence functions appropriately in the board (my constant is very large, Judge Ji, please bear with it)
Real Chain Split
For a point to connect to the edge of all its sons, we select an edge to divide. We call the selected edge a real one and the other a virtual one.
For Shibian, we refer to the son it connects as Shibian.
For a chain composed of real edges, we also call it a real chain.
For each real chain, we build a Splay to maintain information for the entire chain interval.
It is precisely because real chains allow us to make our own choices so that real-chain partitioning can be applied to dynamic tree problems
Convention pastes an abstract diagram of y total
Auxiliary tree splay
An auxiliary tree consists of several Splays, each of which maintains a path in the original tree, and traverses the Splay sequence of points in a middle order, corresponding to a top-down path of the original tree from front to back
Each node of the original tree corresponds to the Splay node of the auxiliary tree one-to-one
The parent node of each Splay's root node should be empty, but the parent node of each Splay's root node in the LCT points to the father node of the chain in the original tree (that is, the father node of the top point of the chain).This kind of father link differs from Splay's father link in that the son knows his father, whereas the father does not know his son, which corresponds to a virtual edge of the original tree. Therefore, the father node at exactly one point in each block of connectivity is empty.
The illustration is as follows (Source: OI-WiKi)
Raw tree:
Corresponding auxiliary trees:
The relationship between auxiliary tree and primitive tree
The solid chains in the original tree are all in the same Splay in the auxiliary tree
Virtual Chain in Original Tree: In the auxiliary tree, the Father of the Splay where the child node is located points to the parent node, but neither of the sons of the parent node points to the child node.
The Father Point of the original tree is not equal to the Father Point of the auxiliary tree.
Auxiliary trees can change roots arbitrarily when they satisfy the properties of auxiliary trees and Splay.
The virtual-real chain transformation can be easily completed on the auxiliary tree, which also implements the dynamic maintenance of tree chain partitioning.
That's a general introduction to LCT. Next, you just need to implement the billion-point function to complete the LCT.
Splay Variations of system functions
pushup(x): What this topic needs to maintain is the exclusive or sum of paths
void pushup(int x)
{
tr[x].sum = tr[tr[x].s[0]].sum ^ tr[x].v ^ tr[tr[x].s[1]].sum;
}
pushdown(x): Unlike the question of flipping intervals, here the lazy marker maintains the modified lazy marker
void pushdown(int x)
{
if (tr[x].rev)
{
pushrev(tr[x].s[0]), pushrev(tr[x].s[1]);
tr[x].rev = 0;
}
}
rotate(int x): In Modification z and y Special judgment on this side y Is it the root node
I've already described it before, and it's splay The root node should not have a parent node, but LCT Here we have this null pointer to maintain the virtual edge
isroot(x) Functions are described later
void rotate(int x)
{
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x; //The only difference
tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
splay(int x): Put Node x Go to Auxiliary Tree splay Root node
Let me first tell you about the different places here, in the past splay When looking for a node, it is always looking down from the root node (as per BST Nature)
But in LCT Medium, splay As a secondary tree, we get splay The node in is the number of the corresponding node in the original tree
In other words, we get it directly splay One of the nodes in the
So, doing it splay When rotating to the root node, we need to download the lazy flag first from top to bottom
This is traditional splay Contradictions
There are two ways to write, one is recursion (less yardage, but a comparison of Judging Ji's mood), the other is iteration ( y Total stack writing)
//Recursive Writing
void update(int x)
{
if (!isroot(x)) update(tr[x].p);
pushdown(x);
}
void splay(int x)
{
update(x);
while (!isroot(x))
{
int y = tr[x].p, z = tr[y].p;
if (!isroot(y))
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
rotate(x);
}
}
//---------------------------------
//Iterative Writing
void splay(int x)
{
int top = 0, r = x;
stk[ ++ top] = r;
while (!isroot(r)) stk[ ++ top] = r = tr[r].p;
while (top) pushdown(stk[top -- ]);
while (!isroot(x))
{
int y = tr[x].p, z = tr[y].p;
if (!isroot(y))
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
rotate(x);
}
}
New Operation
access(x) : Create a path from the root node to x The real chain (which will also x Become corresponding splay Root node)
Go the current node to the root.
Change your son into a previous node.
Update the information of the current point.
Replace the current point with the father of the current point and continue.
void access(int x) //Establish a real chain from the root node to X (while changing x to the root node of the corresponding splay)
{
int z = x; //Record initial node number
for (int y = 0; x; y = x, x = tr[x].p) //x Finds the root along the imaginary edge
{
splay(x); //Go to the root of the current auxiliary tree first
tr[x].s[1] = y, pushup(x); //Connect the previous tree to the middle traverse
}
splay(z); //Turn the initial node to the root
}
makeroot(x) take x Become the root node of the original tree
access(x) After the operation, x Will be rotated to splay Tree roots, at this point we just need to reverse x,You can do the reverse splay Effect of middle traversal
and splay The middle traversal is reversed, which means that in the original tree, from the root node to x The path is reversed so that the x Operation to become root
void makeroot(int x) //Make x the root node of the original tree (and the left subtree is empty)
{
access(x); //In this case, x is the root node of the auxiliary tree, and traverse in reverse order directly.
pushrev(x);
}
findroot(x) : find x The root node of the original tree where it is located, and then rotates the root node of the original tree to the root node of the auxiliary tree
before access(x) From the root node to x Real Chain (at this point) x stay splay Root node), and then find the splay First node traversed in middle order
int findroot(int x) //Find the root node of the original tree where x is located, and rotate the root node of the original tree to the root node of the auxiliary tree
{
access(x); //Break through the real chain from root node to x, where x is currently located at the root node of the secondary tree
while (tr[x].s[0]) pushdown(x), x = tr[x].s[0]; //Find the first element in the secondary tree that is sequentially traversed (lower left corner)
splay(x); //Go to Root Node
return x;
}
split(x, y) : take x reach y Path becomes a real-edge path
Simple, first put x Put it in the root and get through from the root to the root y Path is sufficient
void split(int x, int y) //Change the path from x to y to a real-edge path
{
makeroot(x); //Set x as root first
access(y); //You can just open the real chain from root to y
}
link(x, y) : if x , y If not, join (x, y) This Edge
First put x Put it in the root and look for it y Is the root node of the tree it is in x.
If not (Finding the root node will y Go to the root node of his auxiliary tree) Add an edge
void link(int x, int y) //If x, y are disconnected, join the (x, y) edge
{
makeroot(x); //Set x as root first
if (findroot(y) != x) tr[x].p = y; //If it is not connected, then the real link of x to y is sufficient
}
cut(x, y) : If Edge (x, y) If it exists, delete it ( x, y)This Edge
First put x Put it at the root and judge when:
y Is the root in the same tree x
y Is the parent node of the x
y Is there a left child (middle traverse next to x Back)
Satisfy the above three to illustrate the edge (x,y) Exists, cut fall
void cut(int x, int y) //If an edge (x, y) exists, delete the edge (x, y)
{
makeroot(x);
if (findroot(y) == x && tr[x].s[1] == y && !tr[y].s[0])
{
tr[x].s[1] = tr[y].p = 0;
pushup(x);
}
}
isroot(x) : judge x Is it in the auxiliary tree splay Root node
It's simple. As we said before, he has a father, but his father doesn't recognize his tears
bool isroot(int u) //Determine if u is the top of a real chain
{
return tr[tr[u].p].s[0] != u && tr[tr[u].p].s[1] != u;
}
Some reminders ( From OI-Wiki)
Think about what you don't need before you do anything PushUp perhaps PushDown, LCT For reasons of extra flexibility, Pushdown perhaps Pushup It is possible to change the change to a point that should not be changed at once!
LCT Of Rotate and Splay Not the same, if (z) Always put it in front.
LCT Of Splay The operation is to rotate to the root, not to whose son because it is not needed.
AcWing 2539. Dynamic Tree
Code
The following is the complete code for this topic:
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
struct Splay
{
int s[2], p, v;
int sum, rev;
}tr[N];
bool isroot(int u) //Determine if u is the top of a real chain
{
return tr[tr[u].p].s[0] != u && tr[tr[u].p].s[1] != u;
}
//----------------------------------------------------------\
void pushup(int u)
{
tr[u].sum = tr[tr[u].s[0]].sum ^ tr[u].v ^ tr[tr[u].s[1]].sum;
}
void pushrev(int u)
{
swap(tr[u].s[0], tr[u].s[1]);
tr[u].rev ^= 1;
}
void pushdown(int u)
{
if (tr[u].rev)
{
pushrev(tr[u].s[0]);
pushrev(tr[u].s[1]);
tr[u].rev = 0;
}
}
void rotate(int x)
{
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x; //The only difference
tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x) //Iterative Writing
{
static int stk[N]; //Download Lazy Marks Top Down First
int tt = 0, t = x;
stk[ ++ tt] = t;
while (!isroot(t)) stk[ ++ tt] = t = tr[t].p;
while (tt) pushdown(stk[tt -- ]);
//Next it's basically the same as the splay board
while (!isroot(x))
{
int y = tr[x].p, z = tr[y].p;
if (!isroot(y))
if ((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
else rotate(y);
rotate(x);
}
}
//----------------------------------------------------------\
void access(int x) //Establish a real chain from the root node to X (while changing x to the root node of the corresponding splay)
{
int z = x; //Record initial node number
for (int y = 0; x; y = x, x = tr[x].p) //x Finds the root along the imaginary edge
{
splay(x); //Go to the root of the current auxiliary tree first
tr[x].s[1] = y, pushup(x); //Connect the previous tree to the middle traverse
}
splay(z); //Turn the initial node to the root
}
void makeroot(int x) //Make x the root node of the original tree (and the left subtree is empty)
{
access(x); //In this case, x is the root node of the auxiliary tree, and traverse in reverse order directly.
pushrev(x);
}
int findroot(int x) //Find the root node of the original tree where x is located, and rotate the root node of the original tree to the root node of the auxiliary tree
{
access(x); //Break through the real chain from root node to x, where x is currently located at the root node of the secondary tree
while (tr[x].s[0]) pushdown(x), x = tr[x].s[0]; //Find the first element in the secondary tree that is sequentially traversed (lower left corner)
splay(x); //Go to Root Node
return x;
}
void split(int x, int y) //Change the path from x to y to a real-edge path
{
makeroot(x); //Set x as root first
access(y); //You can just open the real chain from root to y
}
void link(int x, int y) //If x, y are disconnected, join the (x, y) edge
{
makeroot(x); //Set x as root first
if (findroot(y) != x) tr[x].p = y; //If it is not connected, then the real link of x to y is sufficient
}
void cut(int x, int y) //If an edge (x, y) exists, delete the edge (x, y)
{
makeroot(x);
if (findroot(y) == x && tr[x].s[1] == y && !tr[y].s[0])
{
tr[y].p = tr[x].s[1] = 0;
pushup(x);
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &tr[i].v);
while (m -- )
{
int t, x, y;
scanf("%d%d%d", &t, &x, &y);
if (t == 0)
{
split(x, y);
printf("%d\n", tr[y].sum);
}
else if (t == 1) link(x, y);
else if (t == 2) cut(x, y);
else
{
splay(x);
tr[x].v = y;
pushup(x);
}
}
return 0;
}
Author: Colored Pencil
Links: https://www.acwing.com/solution/content/63747/
Source: AcWing
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.
AcWing 999. Magic Forest
LCT + Pre-cheese and Search
Title Description
Given n n n points and m edges.
Each edge contains x, y, a, b, indicating the start, end, minimum limit for a elf, minimum limit for B elf.
Only those carrying more than or equal to the limit can cross this route.
Now find the minimum number of elves to carry from 1 to n (that is, the number of a and b elves).
Topic ideas
Since both a and B are required to pass through an edge, the result must be aiai or bibi for an edge, so the information for a can be fixed to reduce complexity.
That is, each time an edge less than or equal to the aiai size is selected to maintain a path from 1 to n.
So first sort the edges by the number of a, then you only need to maintain the maximum b in the path from 1 to n.
Set bmxbmx to the maximum number of b-elves required on the current path from 1 to n, a i a i to indicate the number of a-elves required on edge i.
Press a to join the edge gradually from small to large. If 1 and N are connected after joining the edge, the elf that represents 1 to n is ai+bmx ai+bmx.
Then the final answer is the minimum value in the process.
Dynamic Edge plus Maintenance Maximum!Direct to LCT.Are you a data structure fool.jpg
Although the title gives you a picture, you only need to maintain a path from 1 to n.
So when adding a new edge makes the maintained tree a graph, you need to find the ring. If the new edge is smaller than the maximum value in the ring, delete the largest edge in the ring and add a new edge.
Why delete the longest side?Since the answer to each edge is ai+bmx ai+bmx, deleting the largest edge and adding an edge smaller than the largest edge will not necessarily increase the answer.
Note: findroot will be stuck, so look it up
Tip: Edge weight to point weight, which can be assigned by adding a new point between two points.
/*
* Ideas:
* Sort all edges in ascending order by a, join edges from smallest to largest, find the maximum value of B in the path from 1 to n on the graph where edges have been added, find the maximum value of b, and update the global minimum answer for the sum of currently enumerated a
* The original point id is from 1 to n, the weight is 0, the edge is abstracted as a point, if there is one edge
* (A, B), The weight value is W and the edge id is i, which is abstracted as a point whose weight is W. Adding an edge (A, B) means adding two edges (A, i+(n+1)) and (B, i+(n+1)) on the graph, so the problem is converted to
* Dynamically maximizes the point weight of B on the path between node 1 and node n. When an edge (A,B) is added, if AB is found to be connected, adding (A,B) will form a ring, and then find A on the graph and the path between B is the largest.
* If max_w > W, the largest edge can be deleted and then added (A,B) without affecting connectivity or causing leaks, if max_w <= W
* Then (A,B) there is no need to add this edge, because it is impossible to get a better understanding by adding this edge. This strategy allows you to keep the graph free of loops and the shape always forest, so you can use dynamic trees to maintain it
* This graph uses the properties of a dynamic tree to quickly find the maximum point weight on a path
*
*/
#include <algorithm>
using namespace std;
// Maximum number of nodes, node number from 1
const int MAX_NODE_NUM = 200005;
// Splay Node
struct Node {
int child[2]; // Two child node IDs
int parent; // Parent node id
int val; // Number of nodes
int max_val; // Maximum value on interval
int max_node_idx; // Number of the point with the largest value
int rev_flag; // Interval flip marks
} __node_pool[MAX_NODE_NUM];
int stack[MAX_NODE_NUM];
// Maximum number of edges
const int MAX_EDGE_NUM = 100005;
// Edge Structures
struct edge_node {
int node1, node2, a, b;
bool operator < (const edge_node& other) const {
return a < other.a;
}
} __edge_nodes[MAX_EDGE_NUM];
int n, m;
// And an array for collection
int pp[MAX_NODE_NUM];
// Flip the left and right subtrees of the current node
void __process_rev(int idx) {
Node& node = __node_pool[idx];
int t = node.child[0];
node.child[0] = node.child[1];
node.child[1] = t;
}
// The result of merging two subtrees
void __push_up(int idx) {
Node& node = __node_pool[idx];
int ans = node.val;
int ans_idx = idx;
if (node.child[0] != 0) {
if (__node_pool[node.child[0]].max_val > ans) {
ans_idx = __node_pool[node.child[0]].max_node_idx;
ans = __node_pool[node.child[0]].max_val;
}
}
if (node.child[1] != 0) {
if (__node_pool[node.child[1]].max_val > ans) {
ans_idx = __node_pool[node.child[1]].max_node_idx;
ans = __node_pool[node.child[1]].max_val;
}
}
node.max_val = ans;
node.max_node_idx = ans_idx;
}
// Download interval flips lazy tag
void __push_down_rev_flag(int idx) {
Node& node = __node_pool[idx];
if (node.rev_flag == 0) {
return;
}
if (node.child[0] != 0) {
__node_pool[node.child[0]].rev_flag ^= 1;
}
if (node.child[1] != 0) {
__node_pool[node.child[1]].rev_flag ^= 1;
}
}
// push_down operation with interval inversion
void __push_down_rev(int idx) {
Node& node = __node_pool[idx];
if (node.rev_flag == 0) {
return;
}
__push_down_rev_flag(idx);
if (node.child[0] != 0) {
__process_rev(node.child[0]);
}
if (node.child[1] != 0) {
__process_rev(node.child[1]);
}
node.rev_flag = 0;
}
// Unified push_down function
void __push_down(int idx) {
__push_down_rev(idx);
}
// Determine whether a node is the root node of its splay
bool is_splay_root(int idx) {
int parent = __node_pool[idx].parent;
return idx != __node_pool[parent].child[0] && idx != __node_pool[parent].child[1];
}
// Modify the value of the lazy tag
void reverse_flag(int idx) {
Node& node = __node_pool[idx];
node.rev_flag ^= 1;
__process_rev(idx); // Modify the lazy tag so that the effect of the tag is applied once on the current node
}
// Unified left-handed and right-handed functions rotate the node numbered x up one level
void __rotate(int x) {
int y = __node_pool[x].parent, z = __node_pool[y].parent;
int k1 = __node_pool[y].child[1] == x, k2 = __node_pool[z].child[1] == y;
// If y is the root of splay, then z's child node pointer represents real edge information and cannot modify z's child node information
if (!is_splay_root(y)) {
__node_pool[z].child[k2] = x;
}
__node_pool[x].parent = z;
__node_pool[y].child[k1] = __node_pool[x].child[k1^1];
__node_pool[__node_pool[x].child[k1^1]].parent = y;
__node_pool[x].child[k1^1] = y;
__node_pool[y].parent = x;
__push_up(y);
__push_up(x);
}
// Use the lazy tags on the Splay corresponding to the real edge path where x is located and rotate x to the root of the Splay
void splay(int x) {
int top = 0;
int r = x;
stack[++top] = x;
while (!is_splay_root(r)) {
r = __node_pool[r].parent;
stack[++top] = r;
}
// push_down once from top to bottom
while (top) {
__push_down(stack[top--]);
}
// Rotate x to the root of the splay to which it belongs
while (!is_splay_root(x)) {
int y = __node_pool[x].parent;
int z = __node_pool[y].parent;
if (!is_splay_root(y)) {
if ((__node_pool[y].child[1] == x) ^ (__node_pool[z].child[1] == y)) {
__rotate(x);
} else {
__rotate(y);
}
}
__rotate(x);
}
}
// Make the path between the root r and X of the dynamic tree to which node x belongs a real edge path and x the root of the splay to which it belongs last
void access(int x) {
int z = x;
for (int y = 0; x != 0; y = x, x = __node_pool[x].parent) {
splay(x);
__node_pool[x].child[1] = y;
__push_up(x);
}
splay(z);
}
// Change x to the root of the entire dynamic tree
void make_root(int x) {
access(x);
reverse_flag(x);
}
// Find the root node id of the dynamic tree to which x belongs and rotate the node to the root of the Play to which it belongs
int find_root(int x) {
access(x);
while (__node_pool[x].child[0] != 0) {
__push_down(x);
x = __node_pool[x].child[0];
}
splay(x);
return x;
}
// Change the path between two nodes x, y to a real edge path and y to the root of the splay to which they belong
void split(int x, int y) {
make_root(x);
access(y);
}
// If x and y are not in a dynamic tree, add a virtual edge from x to y
void link(int x, int y) {
make_root(x);
if (find_root(y) != x) {
__node_pool[x].parent = y;
}
}
// If xy had previously connected edges on a dynamic tree, break that edge
void cut(int x, int y) {
make_root(x);
if (find_root(y) == x && __node_pool[y].parent == x && __node_pool[y].child[0] == 0) {
__node_pool[x].child[1] = __node_pool[y].parent = 0;
__push_up(x);
}
}
int get_root(int node) {
if (pp[node] == node) {
return node;
}
pp[node] = get_root(pp[node]);
return pp[node];
}
void merge(int a, int b) {
int root1 = get_root(a), root2 = get_root(b);
if (root1 != root2) {
pp[root1] = root2;
}
}
bool in_same_set(int a, int b) {
return get_root(a) == get_root(b);
}
// Gets the number of the point with the largest weight on the path from node1 to node2 in the dynamic tree
int get_max_dis_node_idx(int node1, int node2) {
split(node1, node2);
return __node_pool[node2].max_node_idx;
}
// Getting the Maximum Point Weight on the Dynamic Tree from Noe1 to Noe2 Path
int get_max_dis(int node1, int node2) {
split(node1, node2);
return __node_pool[node2].max_val;
}
// Add an edge
void add_edge(int node1, int node2, int edge_node, int w) {
if (in_same_set(node1, node2)) {
int max_node_idx = get_max_dis_node_idx(node1, node2);
int max_weight = __node_pool[max_node_idx].val;
if (max_weight <= w) {
// There's no need to add that side right now, it won't make the answer better
return;
}
cut(max_node_idx, __edge_nodes[max_node_idx - (n+1)].node1);
cut(max_node_idx, __edge_nodes[max_node_idx - (n+1)].node1);
}
link(edge_node, node1);
link(edge_node, node2);
}
int main() {
//freopen("/Users/grh/Programming/CLionProjects/SimpleTest/input.txt", "r", stdin);
int node1, node2, a, b;
scanf("%d %d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d %d %d %d", &(__edge_nodes[i].node1), &(__edge_nodes[i].node2), &(__edge_nodes[i].a), &(__edge_nodes[i].b));
}
// Sort by a-weight
sort(__edge_nodes, __edge_nodes + m);
// The original point weights that already exist on the initial graph are all 0, numbered from 1 to n
for (int i = 1; i <= n; i++) {
__node_pool[i].val = 0;
__node_pool[i].max_val = 0;
__node_pool[i].max_node_idx = i;
pp[i] = i;
}
// Numbers of points abstracted from edges n+1 to n+m
for (int i = 0; i < m; i++) {
__node_pool[i+n+1].val = __edge_nodes[i].b;
__node_pool[i+n+1].max_val = __edge_nodes[i].b;
__node_pool[i+n+1].max_node_idx = i+n+1;
pp[i+n+1] = i+n+1;
}
int ans = 0x7fffffff;
int i = 0;
while (i < m) {
int j = i;
int wei_a = __edge_nodes[i].a;
while (j < m && __edge_nodes[j].a == wei_a) {
if (__edge_nodes[j].node1 != __edge_nodes[j].node2) {
add_edge(__edge_nodes[j].node1, __edge_nodes[j].node2, j+(n+1), __edge_nodes[j].b);
merge(__edge_nodes[j].node1, __edge_nodes[j].node2);
}
j += 1;
}
if (in_same_set(1, n)) {
ans = min(ans, wei_a + get_max_dis(1, n));
}
i = j;
}
if (ans != 0x7fffffff) {
printf("%d\n", ans);
} else {
printf("-1\n");
}
return 0;
}
Author: Keep your head open
Links: https://www.acwing.com/solution/content/48969/
Source: AcWing
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.
Precise coverage of DLX
AcWing 1067.Precise Coverage Problem
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 5510;
int n, m;
int l[N], r[N], u[N], d[N], s[N], row[N], col[N], idx;
int ans[N], top;
void init()
{
for (int i = 0; i <= m; i ++ )
{
l[i] = i - 1, r[i] = i + 1;
u[i] = d[i] = i;
}
l[0] = m, r[m] = 0;
idx = m + 1;
}
void add(int& hh, int& tt, int x, int y)
{
row[idx] = x, col[idx] = y, s[y] ++ ;
u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;
tt = idx ++ ;
}
void remove(int p)
{
r[l[p]] = r[p], l[r[p]] = l[p];
for (int i = d[p]; i != p; i = d[i])
for (int j = r[i]; j != i; j = r[j])
{
s[col[j]] -- ;
u[d[j]] = u[j], d[u[j]] = d[j];
}
}
void resume(int p)
{
for (int i = u[p]; i != p; i = u[i])
for (int j = l[i]; j != i; j = l[j])
{
u[d[j]] = j, d[u[j]] = j;
s[col[j]] ++ ;
}
r[l[p]] = p, l[r[p]] = p;
}
bool dfs()
{
if (!r[0]) return true;
int p = r[0];
for (int i = r[0]; i; i = r[i])
if (s[i] < s[p])
p = i;
remove(p);
for (int i = d[p]; i != p; i = d[i])
{
ans[ ++ top] = row[i];
for (int j = r[i]; j != i; j = r[j]) remove(col[j]);
if (dfs()) return true;
for (int j = l[i]; j != i; j = l[j]) resume(col[j]);
top -- ;
}
resume(p);
return false;
}
int main()
{
scanf("%d%d", &n, &m);
init();
for (int i = 1; i <= n; i ++ )
{
int hh = idx, tt = idx;
for (int j = 1; j <= m; j ++ )
{
int x;
scanf("%d", &x);
if (x) add(hh, tt, i, j);
}
}
if (dfs())
{
for (int i = 1; i <= top; i ++ ) printf("%d ", ans[i]);
puts("");
}
else puts("No Solution!");
return 0;
}
AcWing 169.Sudoku

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20000;
int m = 16 * 16 * 4;
int u[N], d[N], l[N], r[N], s[N], col[N], row[N], idx;
int ans[N], top;
struct Op
{
int x, y;
char z;
}op[N];
char g[20][20];
void init()
{
for (int i = 0; i <= m; i ++ )
{
l[i] = i - 1, r[i] = i + 1;
s[i] = 0;
d[i] = u[i] = i;
}
l[0] = m, r[m] = 0;
idx = m + 1;
}
void add(int& hh, int& tt, int x, int y)
{
row[idx] = x, col[idx] = y, s[y] ++ ;
u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;
tt = idx ++ ;
}
void remove(int p)
{
r[l[p]] = r[p], l[r[p]] = l[p];
for (int i = d[p]; i != p; i = d[i])
for (int j = r[i]; j != i; j = r[j])
{
s[col[j]] -- ;
u[d[j]] = u[j], d[u[j]] = d[j];
}
}
void resume(int p)
{
for (int i = u[p]; i != p; i = u[i])
for (int j = l[i]; j != i; j = l[j])
{
u[d[j]] = j, d[u[j]] = j;
s[col[j]] ++ ;
}
r[l[p]] = p, l[r[p]] = p;
}
bool dfs()
{
if (!r[0]) return true;
int p = r[0];
for (int i = r[0]; i; i = r[i])
if (s[i] < s[p])
p = i;
remove(p);
for (int i = d[p]; i != p; i = d[i])
{
ans[ ++ top] = row[i];
for (int j = r[i]; j != i; j = r[j]) remove(col[j]);
if (dfs()) return true;
for (int j = l[i]; j != i; j = l[j]) resume(col[j]);
top -- ;
}
resume(p);
return false;
}
int main()
{
while (~scanf("%s", g[0]))
{
for (int i = 1; i < 16; i ++ ) scanf("%s", g[i]);
init();
for (int i = 0, n = 1; i < 16; i ++ )
for (int j = 0; j < 16; j ++ )
{
int a = 0, b = 15;
if (g[i][j] != '-') a = b = g[i][j] - 'A';
for (int k = a; k <= b; k ++, n ++ )
{
int hh = idx, tt = idx;
op[n] = {i, j, k + 'A'};
add(hh, tt, n, i * 16 + j + 1);
add(hh, tt, n, 256 + i * 16 + k + 1);
add(hh, tt, n, 256 * 2 + j * 16 + k + 1);
add(hh, tt, n, 256 * 3 + (i / 4 * 4 + j / 4) * 16 + k + 1);
}
}
dfs();
for (int i = 1; i <= top; i ++ )
{
auto t = op[ans[i]];
g[t.x][t.y] = t.z;
}
for (int i = 0; i < 16; i ++ ) puts(g[i]);
puts("");
}
return 0;
}
AcWing 956.Smart Bead Game
Duplicate Overwrite Problem for DLX
AcWing 2713.Duplicate Coverage Problem
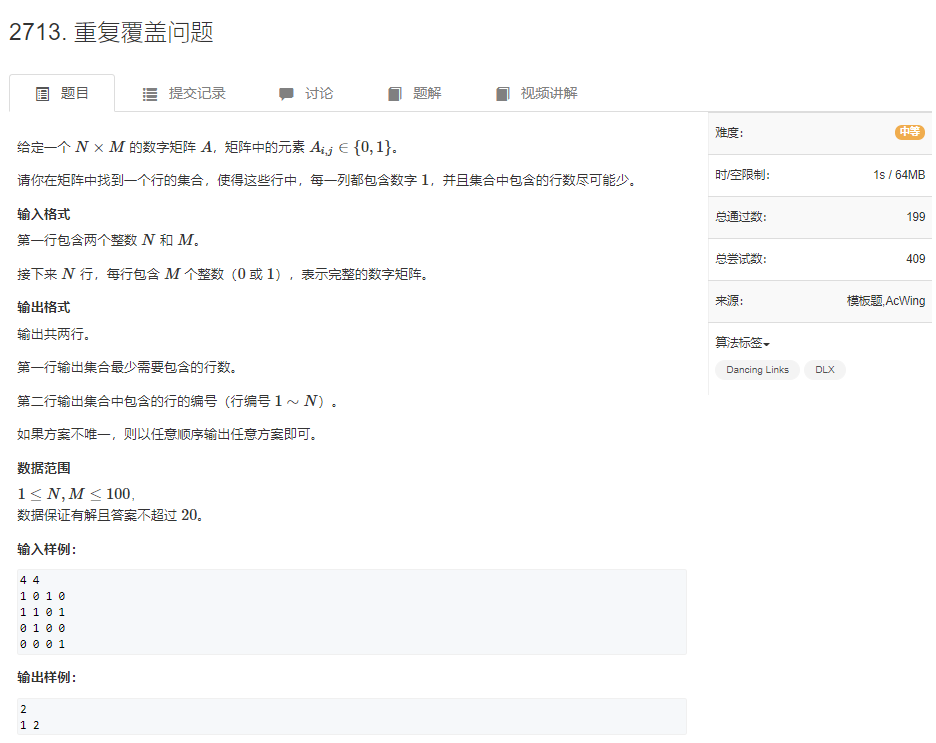
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
int n, m;
int l[N], r[N], u[N], d[N], col[N], row[N], s[N], idx;
int ans[N];
bool st[110];
void init()
{
for (int i = 0; i <= m; i ++ )
{
l[i] = i - 1, r[i] = i + 1;
col[i] = u[i] = d[i] = i;
s[i] = 0;
}
l[0] = m, r[m] = 0;
idx = m + 1;
}
void add(int& hh, int& tt, int x, int y)
{
row[idx] = x, col[idx] = y, s[y] ++ ;
u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;
tt = idx ++ ;
}
int h()
{
int cnt = 0;
memset(st, 0, sizeof st);
for (int i = r[0]; i; i = r[i])
{
if (st[col[i]]) continue;
cnt ++ ;
st[col[i]] = true;
for (int j = d[i]; j != i; j = d[j])
for (int k = r[j]; k != j; k = r[k])
st[col[k]] = true;
}
return cnt;
}
void remove(int p)
{
for (int i = d[p]; i != p; i = d[i])
{
r[l[i]] = r[i];
l[r[i]] = l[i];
}
}
void resume(int p)
{
for (int i = u[p]; i != p; i = u[i])
{
r[l[i]] = i;
l[r[i]] = i;
}
}
bool dfs(int k, int depth)
{
if (k + h() > depth) return false;
if (!r[0]) return true;
int p = r[0];
for (int i = r[0]; i; i = r[i])
if (s[p] > s[i])
p = i;
for (int i = d[p]; i != p; i = d[i])
{
ans[k] = row[i];
remove(i);
for (int j = r[i]; j != i; j = r[j]) remove(j);
if (dfs(k + 1, depth)) return true;
for (int j = l[i]; j != i; j = l[j]) resume(j);
resume(i);
}
return false;
}
int main()
{
scanf("%d%d", &n, &m);
init();
for (int i = 1; i <= n; i ++ )
{
int hh = idx, tt = idx;
for (int j = 1; j <= m; j ++ )
{
int x;
scanf("%d", &x);
if (x) add(hh, tt, i, j);
}
}
int depth = 0;
while (!dfs(0, depth)) depth ++ ;
printf("%d\n", depth);
for (int i = 0; i < depth; i ++ ) printf("%d ", ans[i]);
return 0;
}
AcWing 182.Destroy Square
AcWing 2724.radar
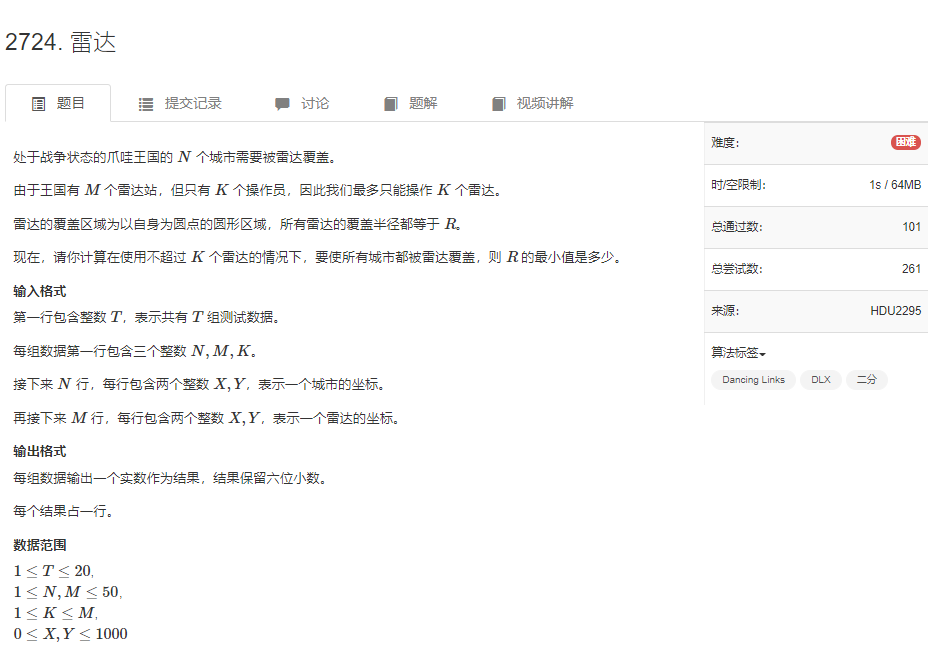
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 55, M = N * N;
int n, m, k;
int l[M], r[M], u[M], d[M], row[M], col[M], s[M], idx;
bool st[N];
PDD city[N], station[N];
void init()
{
for (int i = 0; i <= n; i ++ )
{
l[i] = i - 1, r[i] = i + 1;
col[i] = u[i] = d[i] = i;
s[i] = 0;
}
l[0] = n, r[n] = 0;
idx = n + 1;
}
void add(int& hh, int& tt, int x, int y)
{
row[idx] = x, col[idx] = y, s[y] ++ ;
u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;
tt = idx ++ ;
}
int h()
{
int res = 0;
memset(st, 0, sizeof st);
for (int i = r[0]; i; i = r[i])
{
if (st[i]) continue;
res ++ ;
st[i] = true;
for (int j = d[i]; j != i; j = d[j])
for (int k = r[j]; k != j; k = r[k])
st[col[k]] = true;
}
return res;
}
void remove(int p)
{
for (int i = d[p]; i != p; i = d[i])
{
r[l[i]] = r[i];
l[r[i]] = l[i];
}
}
void resume(int p)
{
for (int i = u[p]; i != p; i = u[i])
{
r[l[i]] = i;
l[r[i]] = i;
}
}
bool dfs(int k, int depth)
{
if (k + h() > depth) return false;
if (!r[0]) return true;
int p = r[0];
for (int i = r[0]; i; i = r[i])
if (s[p] > s[i])
p = i;
for (int i = d[p]; i != p; i = d[i])
{
remove(i);
for (int j = r[i]; j != i; j = r[j]) remove(j);
if (dfs(k + 1, depth)) return true;
for (int j = l[i]; j != i; j = l[j]) resume(j);
resume(i);
}
return false;
}
bool check(PDD a, PDD b, double mid)
{
double dx = a.x - b.x;
double dy = a.y - b.y;
return dx * dx + dy * dy <= mid * mid;
}
bool check(double mid)
{
init();
for (int i = 1; i <= m; i ++ )
{
int hh = idx, tt = idx;
for (int j = 1; j <= n; j ++ )
if (check(station[i], city[j], mid))
add(hh, tt, i, j);
}
int depth = 0;
while (depth <= k && !dfs(0, depth)) depth ++ ;
return depth <= k;
}
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; i ++ ) scanf("%lf%lf", &city[i].x, &city[i].y);
for (int i = 1; i <= m; i ++ ) scanf("%lf%lf", &station[i].x, &station[i].y);
double l = 0, r = 2000;
while (r - l > 1e-10)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
printf("%lf\n", r);
}
return 0;
}
Left Partial Tree
AcWing 2714.Left Partial Tree
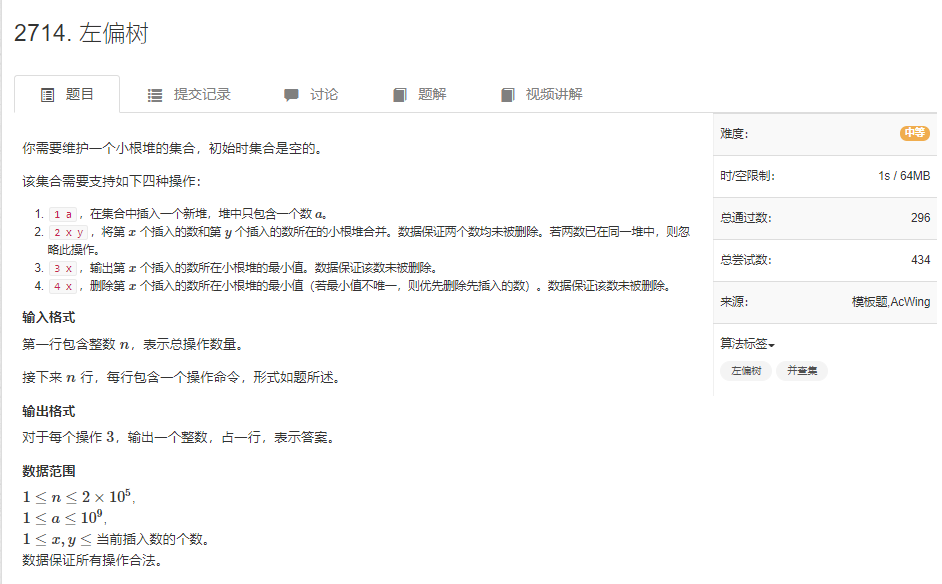
/*
Forest Realization with Left Deflection Tree
The following operations are supported:
1. Construct a new left skewed tree heap make_new_heap(val) with a numeric value, returning the id number of the new node
2. Combines the left-skewed tree where the Id1 element is located with the left-skewed tree merge(id1, id2) where the Id2 element is located, returning the ID number of the root of the new left-skewed tree
3. Place the new value Valin the left-hand skewed tree put(id, val) where the number ID exists, and return the ID number of the new node where the value is val
4. Query the value get_top_val(id) of the top heap element of the heap where the ID number element is located to return a tuple of top heap element(id, val)
5. Remove the top element of the heap where the ID number is located from the heap, pop_top_val(id), and return the top element (id, val) binary
6. get_val(id) directly from the node's ID number
Be careful:
All IDs are generated internally by the left skewed tree data structure itself, and can only be acquired externally. You cannot create any id number yourself
0 Number node indicates invalid meaning, all valid nodes have id numbers greater than or equal to 1
id = 0 The heap where the node is located represents an empty heap
Code Template 2714.Title of skewed left tree is blueprint
Input data format
1 a,Insert a new heap into the collection containing only one number a.
2 x y,Merge the number of Xth inserts with the small root heap where the number of YTH inserts is located. The data ensures that neither number is deleted. If both numbers are alread y in the same heap, this operation is ignored.
3 x,The minimum value of the smallest root heap in which the number inserted Xth of the output is located. The data ensures that the number is not deleted.
4 x,Delete the minimum value of the smallest root heap where the number of Xth inserts is located (if the minimum value is not unique, the number inserted first is deleted first). The data ensures that the number is not deleted.
*/
#include <stdio.h>
#include <algorithm>
using namespace std;
const int MAX_NODE_NUN = 200100;
int ll[MAX_NODE_NUN]; // Left Pointer
int rr[MAX_NODE_NUN]; // Right Pointer
int val[MAX_NODE_NUN]; // In the actual problem, the node value is not necessarily the int type. In the actual use, modify it according to the specific situation, and correspond to the template parameter T, which requires T type to implement less than operator
int dis[MAX_NODE_NUN]; // Distance of nodes
int pp[MAX_NODE_NUN]; // And set arrays
int __buffer[MAX_NODE_NUN]; // Cache and use when collecting operations
int __pool_pos = 1; // End of current object pool
template<typename T>
class LeftistHeapForest {
// Get and lookup the root id in the set
int __get_union_find_root(int node) {
int pos = 0;
int p = node;
while (p != pp[p]) {
__buffer[pos++] = p;
p = pp[p];
}
for (int i = 0; i < pos; i++) {
pp[__buffer[i]] = p;
}
return p;
}
// Is it in the same and checked set
bool __in_same_union_find(int id1, int id2) {
return __get_union_find_root(id1) == __get_union_find_root(id2);
}
// And look up the collection and merge
void __merge_union_find(int id1, int id2) {
pp[__get_union_find_root(id1)] = __get_union_find_root(id2);
}
// And set modification root id
void __change_union_find_root_id(int id) {
pp[__get_union_find_root(id)] = id;
pp[id] = id;
}
// The merged root is id1 and the root is id2 heaps, returning the id number of the heap top node of the new heap
int __merge(int id1, int id2) {
if (id1 == 0 || id2 == 0) {
return id1 + id2;
}
T val1 = val[id1], val2 = val[id2];
if (val2 < val1 || (val1 == val2 && id2 < id1)) {
id1 = id1 ^ id2, id2 = id1 ^ id2, id1 = id1 ^ id2;
}
int new_root_id = __merge(rr[id1], id2);
rr[id1] = new_root_id;
dis[id1] = dis[new_root_id] + 1;
int l_id = ll[id1], r_id = rr[id1];
if (dis[r_id] > dis[l_id]) {
ll[id1] = r_id, rr[id1] = l_id;
}
return id1;
}
public:
// Create a new heap with the value v, returning the id of the newly created node
int make_new_heap(T v) {
int id = __pool_pos++;
ll[id] = rr[id] = dis[id] = 0;
val[id] = v;
pp[id] = id;
return id;
}
// Merge the heap where id1 is located with the heap where id2 is located to return the id of the top element of the new heap
int merge(int id1, int id2) {
if (id1 == 0 || id2 == 0) {
return __get_union_find_root(id1 + id2);
}
if (__in_same_union_find(id1, id2)) {
return __get_union_find_root(id1);
}
int new_root_id = __merge(__get_union_find_root(id1), __get_union_find_root(id2));
__merge_union_find(id1, id2); // Two trees merge in and collect
__change_union_find_root_id(new_root_id); // Replace the root of the union set where the new root is located with the new root itself
return new_root_id;
}
// Place the new val ue Valin the left partial tree of the node with id number, and return the new node id number
int put(int id, T val) {
int new_id = make_new_heap(val);
merge(new_id, id);
return new_id;
}
// Gets the top element of the heap on which the node ID is located (heap top id, heap top val)
pair<int, T> get_top_val(int id) {
int top_id = __get_union_find_root(id);
return pair<int, T>{top_id, val[top_id]};
}
// Remove the top element of the heap where the ID number is located from the heap and return the top element (heap top id, heap top val)
pair<int, T> pop_top_val(int id) {
int top_id = __get_union_find_root(id);
int new_root_id = __merge(ll[top_id], rr[top_id]);
__change_union_find_root_id(new_root_id);
return pair<int, T>{top_id, val[top_id]};
}
};
int main() {
//freopen("/Users/grh/Programming/CLionProjects/SimpleTest/input.txt", "r", stdin);
LeftistHeapForest<int> algo;
int n, op;
int a, b;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &op);
switch(op) {
case 1:
scanf("%d", &a);
algo.make_new_heap(a);
break;
case 2:
scanf("%d %d", &a, &b);
algo.merge(a, b);
break;
case 3:
scanf("%d", &a);
printf("%d\n", algo.get_top_val(a).second);
break;
case 4:
scanf("%d", &a);
algo.pop_top_val(a);
break;
default:
break;
}
}
return 0;
}
2646.Tricky operation

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=3e5+10;
struct qnode{
char op[3];
int x,y;
}p[N];
struct node{
int to,next;
}a[N];
int n,q,tot,cnt,ls[N],w[N],fa[N],l[N],r[N];
struct SegTree{
int w[N<<2],lazy[N<<2];
void Downdata(int x){
if(!lazy[x])return;
w[x*2]+=lazy[x];lazy[x*2]+=lazy[x];
w[x*2+1]+=lazy[x];lazy[x*2+1]+=lazy[x];
lazy[x]=0;return;
}
void Change(int x,int L,int R,int l,int r,int val){
if(L==l&&R==r){w[x]+=val;lazy[x]+=val;return;}
int mid=(L+R)>>1;Downdata(x);
if(r<=mid)Change(x*2,L,mid,l,r,val);
else if(l>mid)Change(x*2+1,mid+1,R,l,r,val);
else Change(x*2,L,mid,l,mid,val),Change(x*2+1,mid+1,R,mid+1,r,val);
w[x]=max(w[x*2],w[x*2+1]);return;
}
int Ask(int x,int L,int R,int l,int r){
if(L==l&&R==r){return w[x];}
int mid=(L+R)>>1;Downdata(x);
if(r<=mid)return Ask(x*2,L,mid,l,r);
if(l>mid)return Ask(x*2+1,mid+1,R,l,r);
return max(Ask(x*2,L,mid,l,mid),Ask(x*2+1,mid+1,R,mid+1,r));
}
}T;
void addl(int x,int y){
if(x==y)return;
a[++tot].to=y;
a[tot].next=ls[x];
ls[x]=tot;return;
}
int find(int x)
{return (fa[x]==x)?x:(fa[x]=find(fa[x]));}
void dfs(int x){
l[x]=r[x]=++cnt;T.Change(1,1,n,cnt,cnt,w[x]);
for(int i=ls[x];i;i=a[i].next)
dfs(a[i].to);
return;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&w[i]),fa[i]=i;
scanf("%d",&q);
for(int i=1;i<=q;i++){
scanf("%s",p[i].op);
if(p[i].op[0]=='U'){
scanf("%d%d",&p[i].x,&p[i].y);
p[i].x=find(p[i].x);p[i].y=find(p[i].y);
if(p[i].x==p[i].y)continue;
if(p[i].x<p[i].y)swap(p[i].x,p[i].y);
fa[p[i].y]=p[i].x;
}
else if(p[i].op[0]=='A'&&p[i].op[1]=='1')
scanf("%d%d",&p[i].x,&p[i].y);
else if(p[i].op[0]=='A'&&p[i].op[1]=='2')
scanf("%d%d",&p[i].x,&p[i].y);
else if(p[i].op[0]!='F'||p[i].op[1]!='3')
scanf("%d",&p[i].x);
}
for(int i=q;i>=1;i--)
if(p[i].op[0]=='U')addl(p[i].x,p[i].y);
for(int i=1;i<=n;i++)
if(find(i)==i)dfs(i);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=q;i++){
int x=p[i].x,y=p[i].y;
if(p[i].op[0]=='U'){
if(x==y)continue;
fa[y]=x;r[x]=r[y];
}
else if(p[i].op[0]=='A'&&p[i].op[1]=='1')
T.Change(1,1,n,l[x],l[x],y);
else if(p[i].op[0]=='A'&&p[i].op[1]=='2')
x=find(x),T.Change(1,1,n,l[x],r[x],y);
else if(p[i].op[0]=='A'&&p[i].op[1]=='3')
T.Change(1,1,n,1,n,x);
else if(p[i].op[0]=='F'&&p[i].op[1]=='1')
printf("%d\n",T.Ask(1,1,n,l[x],l[x]));
else if(p[i].op[0]=='F'&&p[i].op[1]=='2')
x=find(x),printf("%d\n",T.Ask(1,1,n,l[x],r[x]));
else printf("%d\n",T.Ask(1,1,n,1,n));
}
return 0;
}
AcWing 2725.Number Sequence
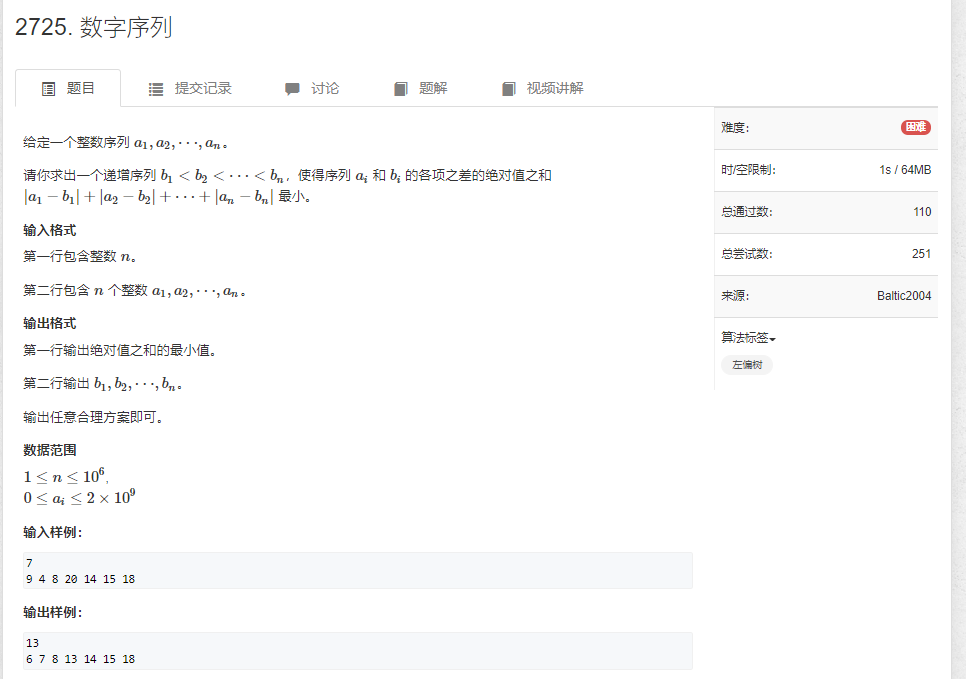
#include <stdio.h>
#include <algorithm>
using namespace std;
const int MAX_NODE_NUN = 2001000;
struct range_node {
int start, end; // Interval start and end positions
int root_id; // Root id of the left-hand tree
} ranges[MAX_NODE_NUN];
int range_idx = 0;
int ll[MAX_NODE_NUN]; // Left Pointer
int rr[MAX_NODE_NUN]; // Right Pointer
long long val[MAX_NODE_NUN]; // In the actual problem, the node value is not necessarily the int type. In the actual use, modify it according to the specific situation, and correspond to the template parameter T, which requires T type to implement less than operator
int dis[MAX_NODE_NUN]; // Distance of nodes
int pp[MAX_NODE_NUN]; // And set arrays
int __buffer[MAX_NODE_NUN]; // Cache and use when collecting operations
int __pool_pos = 1; // End of current object pool
long long arr[MAX_NODE_NUN];
template<typename T>
class LeftistHeapForest {
// The merged root is id1 and the root is id2 heaps, returning the id number of the heap top node of the new heap
int __merge(int id1, int id2) {
if (id1 == 0 || id2 == 0) {
return id1 + id2;
}
T val1 = val[id1], val2 = val[id2];
if (val2 > val1 || (val1 == val2 && id2 < id1)) {
id1 = id1 ^ id2, id2 = id1 ^ id2, id1 = id1 ^ id2;
}
int new_root_id = __merge(rr[id1], id2);
rr[id1] = new_root_id;
dis[id1] = dis[new_root_id] + 1;
int l_id = ll[id1], r_id = rr[id1];
if (dis[r_id] > dis[l_id]) {
ll[id1] = r_id, rr[id1] = l_id;
}
return id1;
}
public:
LeftistHeapForest() {
__pool_pos = 1;
}
// Create a new heap with the value v, returning the id of the newly created node
int make_new_heap(T v) {
int id = __pool_pos++;
ll[id] = rr[id] = dis[id] = 0;
val[id] = v;
return id;
}
// The merge heap top is the heap root1 and the heap top is the heap root2, returning the id of the heap top element of the new heap
int merge(int root1, int root2) {
return __merge(root1, root2);
}
// Gets the top element (top id, top val) of the heap on which the node with ID is located
T get_top_val(int root) {
return val[root];
}
// Remove the top element of a heap whose top is the root node from the heap and return (new heap top id, popped heap top val)
pair<int, T> pop_top_val(int root) {
int new_root_id = __merge(ll[root], rr[root]);
return pair<int, T>{new_root_id, val[root]};
}
};
int main() {
//freopen("/Users/grh/Programming/CLionProjects/SimpleTest/input.txt", "r", stdin);
int n;
long long node_val, prev_val;
scanf("%d", &n);
LeftistHeapForest<long long> algo;
scanf("%lld", &node_val);
arr[0] = node_val;
ranges[range_idx++] = {0, 0, algo.make_new_heap(node_val)};
for (int i = 1; i < n; i++) {
scanf("%lld", &node_val);
arr[i] = node_val;
node_val -= i; // a'[i] = a[i] - i for mapping
ranges[range_idx++] = {i, i, algo.make_new_heap(node_val)};
while (range_idx >= 2) {
node_val = val[ranges[range_idx-1].root_id];
prev_val = val[ranges[range_idx-2].root_id];
if (node_val >= prev_val) {
break;
}
int new_root = algo.merge(ranges[range_idx-1].root_id, ranges[range_idx-2].root_id);
if (((ranges[range_idx-1].end - ranges[range_idx-1].start + 1) & 1) && ((ranges[range_idx-2].end - ranges[range_idx-2].start + 1) & 1)) {
// Both left deflection trees are odd in size, maintain a median, and merge to add one more node to the new heap.
new_root = algo.pop_top_val(new_root).first;
}
ranges[range_idx-2] = {ranges[range_idx-2].start, ranges[range_idx-1].end, new_root};
range_idx -= 1;
}
}
long long ans = 0;
for (int i = 0; i < range_idx; i++) {
long long top_val = val[ranges[i].root_id];
for (int j = ranges[i].start; j <= ranges[i].end; j++) {
ans += abs((top_val + j) - arr[j]);
}
}
printf("%lld\n", ans);
for (int i = 0; i < range_idx; i++) {
long long top_val = val[ranges[i].root_id]; // The top of the heap is the median of the segment, which is the solution of b'[i] for the entire interval
for (int j = ranges[i].start; j <= ranges[i].end; j++) {
printf("%lld ", top_val+j); // b[i] = b'[i] + i, mapped back to the solution b sequence corresponding to the original a sequence
}
}
printf("\n");
}
AcWing 2721.K-Monotonicity

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int f[N][11], cost[N][N];
int w[N], v[N], dist[N], l[N], r[N];
struct Segment
{
int root;
int tot_sum, tot_size;
int tree_sum, tree_size;
int get_cost()
{
int mid = v[root];
return mid * tree_size - tree_sum + tot_sum - tree_sum - (tot_size - tree_size) * mid;
}
}stk[N];
int merge(int x, int y)
{
if (!x || !y) return x + y;
if (v[x] < v[y]) swap(x, y);
r[x] = merge(r[x], y);
if (dist[l[x]] < dist[r[x]]) swap(l[x], r[x]);
dist[x] = dist[r[x]] + 1;
return x;
}
int pop(int x)
{
return merge(l[x], r[x]);
}
void get_cost(int u)
{
int tt = 0, res = 0;
for (int i = u; i <= n; i ++ )
{
auto cur = Segment({i, v[i], 1, v[i], 1});
l[i] = r[i] = 0, dist[i] = 1;
while (tt && v[cur.root] < v[stk[tt].root])
{
res -= stk[tt].get_cost();
cur.root = merge(cur.root, stk[tt].root);
bool is_pop = cur.tot_size % 2 && stk[tt].tot_size % 2;
cur.tot_size += stk[tt].tot_size;
cur.tot_sum += stk[tt].tot_sum;
cur.tree_size += stk[tt].tree_size;
cur.tree_sum += stk[tt].tree_sum;
if (is_pop)
{
cur.tree_size --;
cur.tree_sum -= v[cur.root];
cur.root = pop(cur.root);
}
tt -- ;
}
stk[ ++ tt] = cur;
res += cur.get_cost();
cost[u][i] = min(cost[u][i], res);
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
memset(cost, 0x3f, sizeof cost);
for (int i = 1; i <= n; i ++ ) v[i] = w[i] - i;
for (int i = 1; i <= n; i ++ ) get_cost(i);
for (int i = 1; i <= n; i ++ ) v[i] = -w[i] - i;
for (int i = 1; i <= n; i ++ ) get_cost(i);
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
for (int k = 1; k <= i; k ++ )
f[i][j] = min(f[i][j], f[i - k][j - 1] + cost[i - k + 1][i]);
printf("%d\n", f[n][m]);
return 0;
}
Suffix Array
AcWing 2715.Suffix Array
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int n, m;
char s[N];
int sa[N], x[N], y[N], c[N], rk[N], height[N];
void get_sa()
{
for (int i = 1; i <= n; i ++ ) c[x[i] = s[i]] ++ ;
for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];
for (int i = n; i; i -- ) sa[c[x[i]] -- ] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
for (int i = n - k + 1; i <= n; i ++ ) y[ ++ num] = i;
for (int i = 1; i <= n; i ++ )
if (sa[i] > k)
y[ ++ num] = sa[i] - k;
for (int i = 1; i <= m; i ++ ) c[i] = 0;
for (int i = 1; i <= n; i ++ ) c[x[i]] ++ ;
for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];
for (int i = n; i; i -- ) sa[c[x[y[i]]] -- ] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i ++ )
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++ num;
if (num == n) break;
m = num;
}
}
void get_height()
{
for (int i = 1; i <= n; i ++ ) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i ++ )
{
if (rk[i] == 1) continue;
if (k) k -- ;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k ++ ;
height[rk[i]] = k;
}
}
int main()
{
scanf("%s", s + 1);
n = strlen(s + 1), m = 122;
get_sa();
get_height();
for (int i = 1; i <= n; i ++ ) printf("%d ", sa[i]);
puts("");
for (int i = 1; i <= n; i ++ ) printf("%d ", height[i]);
puts("");
return 0;
}
AcWing 1004.Grandeur of Wine
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<LL, LL> PLL;
const int N = 300010;
const LL INF = 2e18;
int n, m;
char s[N];
int sa[N], x[N], y[N], c[N], rk[N], height[N];
int w[N], p[N], sz[N];
LL max1[N], max2[N], min1[N], min2[N];
vector<int> hs[N];
PLL ans[N];
void get_sa()
{
for (int i = 1; i <= n; i ++ ) c[x[i] = s[i]] ++ ;
for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];
for (int i = n; i; i -- ) sa[c[x[i]] -- ] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
for (int i = n - k + 1; i <= n; i ++ ) y[ ++ num] = i;
for (int i = 1; i <= n; i ++ )
if (sa[i] > k)
y[ ++ num] = sa[i] - k;
for (int i = 1; i <= m; i ++ ) c[i] = 0;
for (int i = 1; i <= n; i ++ ) c[x[i]] ++ ;
for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];
for (int i = n; i; i -- ) sa[c[x[y[i]]] -- ] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i ++ )
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++ num;
if (num == n) break;
m = num;
}
}
void get_height()
{
for (int i = 1; i <= n; i ++ ) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i ++ )
{
if (rk[i] == 1) continue;
if (k) k -- ;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k ++ ;
height[rk[i]] = k;
}
}
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
LL get(int x)
{
return x * (x - 1ll) / 2;
}
PLL calc(int r)
{
static LL cnt = 0, maxv = -INF;
for (auto x: hs[r])
{
int a = find(x - 1), b = find(x);
cnt -= get(sz[a]) + get(sz[b]);
p[a] = b;
sz[b] += sz[a];
cnt += get(sz[b]);
if (max1[a] >= max1[b])
{
max2[b] = max(max1[b], max2[a]);
max1[b] = max1[a];
}
else if (max1[a] > max2[b]) max2[b] = max1[a];
if (min1[a] <= min1[b])
{
min2[b] = min(min1[b], min2[a]);
min1[b] = min1[a];
}
else if (min1[a] < min2[b]) min2[b] = min1[a];
maxv = max(maxv, max(max1[b] * max2[b], min1[b] * min2[b]));
}
if (maxv == -INF) return {cnt, 0};
return {cnt, maxv};
}
int main()
{
scanf("%d", &n), m = 122;
scanf("%s", s + 1);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
get_sa();
get_height();
for (int i = 2; i <= n; i ++ ) hs[height[i]].push_back(i);
for (int i = 1; i <= n; i ++ )
{
p[i] = i, sz[i] = 1;
max1[i] = min1[i] = w[sa[i]];
max2[i] = -INF, min2[i] = INF;
}
for (int i = n - 1; i >= 0; i -- ) ans[i] = calc(i);
for (int i = 0; i < n; i ++ ) printf("%lld %lld\n", ans[i].x, ans[i].y);
return 0;
}
.
AcWing 2572.Generate a magic spell
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, m;
int s[N];
int sa[N], x[N], y[N], c[N], rk[N], height[N];
int u[N], d[N];
LL ans[N];
int get(int x)
{
static unordered_map<int, int> hash;
if (hash.count(x) == 0) hash[x] = ++ m;
return hash[x];
}
void get_sa()
{
for (int i = 1; i <= n; i ++ ) c[x[i] = s[i]] ++ ;
for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];
for (int i = n; i; i -- ) sa[c[x[i]] -- ] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
for (int i = n - k + 1; i <= n; i ++ ) y[ ++ num] = i;
for (int i = 1; i <= n; i ++ )
if (sa[i] > k)
y[ ++ num] = sa[i] - k;
for (int i = 1; i <= m; i ++ ) c[i] = 0;
for (int i = 1; i <= n; i ++ ) c[x[i]] ++ ;
for (int i = 2; i <= m; i ++ ) c[i] += c[i - 1];
for (int i = n; i; i -- ) sa[c[x[y[i]]] -- ] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i ++ )
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++ num;
if (num == n) break;
m = num;
}
}
void get_height()
{
for (int i = 1; i <= n; i ++ ) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i ++ )
{
if (rk[i] == 1) continue;
if (k) k -- ;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k ++ ;
height[rk[i]] = k;
}
}
int main()
{
scanf("%d", &n);
for (int i = n; i; i -- ) scanf("%d", &s[i]), s[i] = get(s[i]);
get_sa();
get_height();
LL res = 0;
for (int i = 1; i <= n; i ++ )
{
res += n - sa[i] + 1 - height[i];
u[i] = i - 1, d[i] = i + 1;
}
d[0] = 1, u[n + 1] = n;
for (int i = 1; i <= n; i ++ )
{
ans[i] = res;
int k = rk[i], j = d[k];
res -= n - sa[k] + 1 - height[k];
res -= n - sa[j] + 1 - height[j];
height[j] = min(height[j], height[k]);
res += n - sa[j] + 1 - height[j];
d[u[k]] = d[k], u[d[k]] = u[k];
}
for (int i = n; i; i -- ) printf("%lld\n", ans[i]);
return 0;
}
Suffix Automaton

AcWing 2766.Suffix Automaton
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2000010;
int tot = 1, last = 1;
struct Node
{
int len, fa;
int ch[26];
}node[N];
char str[N];
LL f[N], ans;
int h[N], e[N], ne[N], idx;
void extend(int c)
{
int p = last, np = last = ++ tot;
f[tot] = 1;
node[np].len = node[p].len + 1;
for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;
if (!p) node[np].fa = 1;
else
{
int q = node[p].ch[c];
if (node[q].len == node[p].len + 1) node[np].fa = q;
else
{
int nq = ++ tot;
node[nq] = node[q], node[nq].len = node[p].len + 1;
node[q].fa = node[np].fa = nq;
for (; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
}
}
}
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
for (int i = h[u]; ~i; i = ne[i])
{
dfs(e[i]);
f[u] += f[e[i]];
}
if (f[u] > 1) ans = max(ans, f[u] * node[u].len);
}
int main()
{
scanf("%s", str);
for (int i = 0; str[i]; i ++ ) extend(str[i] - 'a');
memset(h, -1, sizeof h);
for (int i = 2; i <= tot; i ++ ) add(node[i].fa, i);
dfs(1);
printf("%lld\n", ans);
return 0;
}
AcWing 1283.Basaltic Code
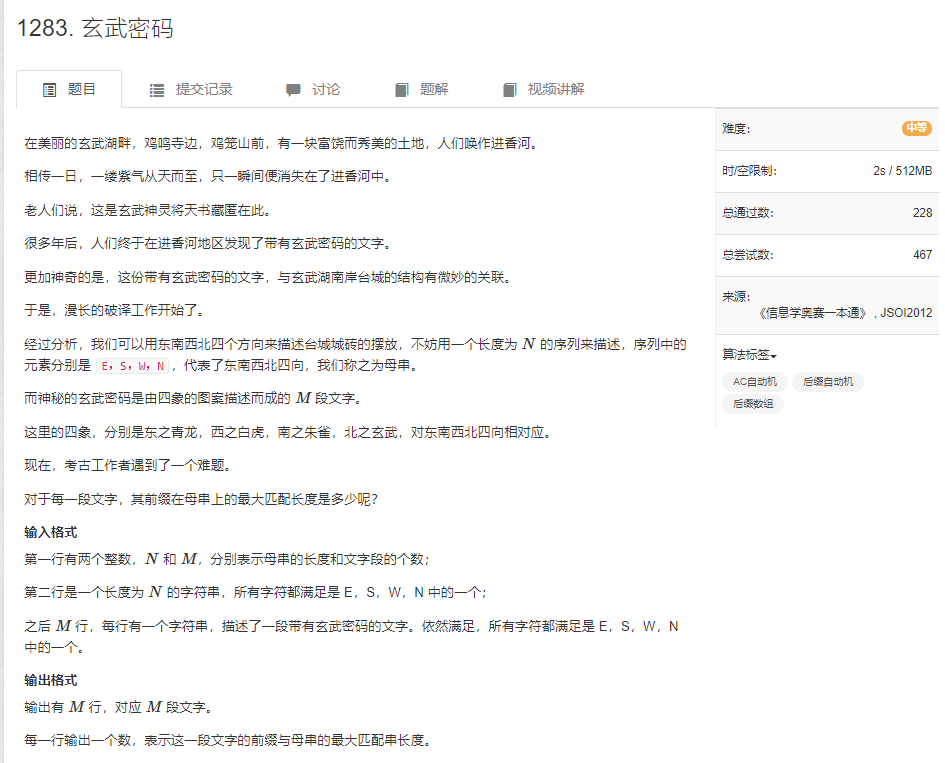
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
const int N = 10000010;
int n, m;
int tot = 1, last = 1;
char str[N];
struct Node
{
int len, fa;
int ch[4];
}node[N * 2];
inline int get(char c)
{
if (c == 'E') return 0;
if (c == 'S') return 1;
if (c == 'W') return 2;
return 3;
}
void extend(int c)
{
int p = last, np = last = ++ tot;
node[np].len = node[p].len + 1;
for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;
if (!p) node[np].fa = 1;
else
{
int q = node[p].ch[c];
if (node[q].len == node[p].len + 1) node[np].fa = q;
else
{
int nq = ++ tot;
node[nq] = node[q], node[nq].len = node[p].len + 1;
node[q].fa = node[np].fa = nq;
for (; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
}
}
}
int main()
{
scanf("%d%d", &n, &m);
scanf("%s", str);
for (int i = 0; str[i]; i ++ ) extend(get(str[i]));
while (m -- )
{
scanf("%s", str);
int p = 1, res = 0;
for (int i = 0; str[i]; i ++ )
{
int c = get(str[i]);
if (node[p].ch[c]) p = node[p].ch[c], res ++ ;
else break;
}
printf("%d\n", res);
}
return 0;
}
AcWing 2811.Longest Common Substring
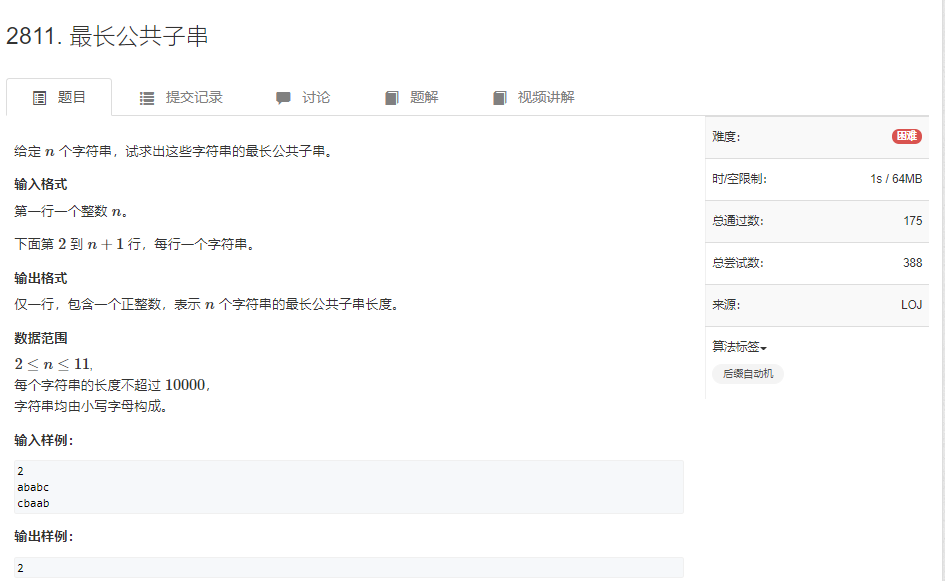
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20010;
int n;
int tot = 1, last = 1;
char str[N];
struct Node
{
int len, fa;
int ch[26];
}node[N];
int ans[N], now[N];
int h[N], e[N], ne[N], idx;
void extend(int c)
{
int p = last, np = last = ++ tot;
node[np].len = node[p].len + 1;
for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;
if (!p) node[np].fa = 1;
else
{
int q = node[p].ch[c];
if (node[q].len == node[p].len + 1) node[np].fa = q;
else
{
int nq = ++ tot;
node[nq] = node[q], node[nq].len = node[p].len + 1;
node[q].fa = node[np].fa = nq;
for (; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
}
}
}
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
for (int i = h[u]; ~i; i = ne[i])
{
dfs(e[i]);
now[u] = max(now[u], now[e[i]]);
}
}
int main()
{
scanf("%d", &n);
scanf("%s", str);
for (int i = 0; str[i]; i ++ ) extend(str[i] - 'a');
for (int i = 1; i <= tot; i ++ ) ans[i] = node[i].len;
memset(h, -1, sizeof h);
for (int i = 2; i <= tot; i ++ ) add(node[i].fa, i);
for (int i = 0; i < n - 1; i ++ )
{
scanf("%s", str);
memset(now, 0, sizeof now);
int p = 1, t = 0;
for (int j = 0; str[j]; j ++ )
{
int c = str[j] - 'a';
while (p > 1 && !node[p].ch[c]) p = node[p].fa, t = node[p].len;
if (node[p].ch[c]) p = node[p].ch[c], t ++ ;
now[p] = max(now[p], t);
}
dfs(1);
for (int j = 1; j <= tot; j ++ ) ans[j] = min(ans[j], now[j]);
}
int res = 0;
for (int i = 1; i <= tot; i ++ ) res = max(res, ans[i]);
printf("%d\n", res);
return 0;
}
Spot Division
AcWing 252.tree
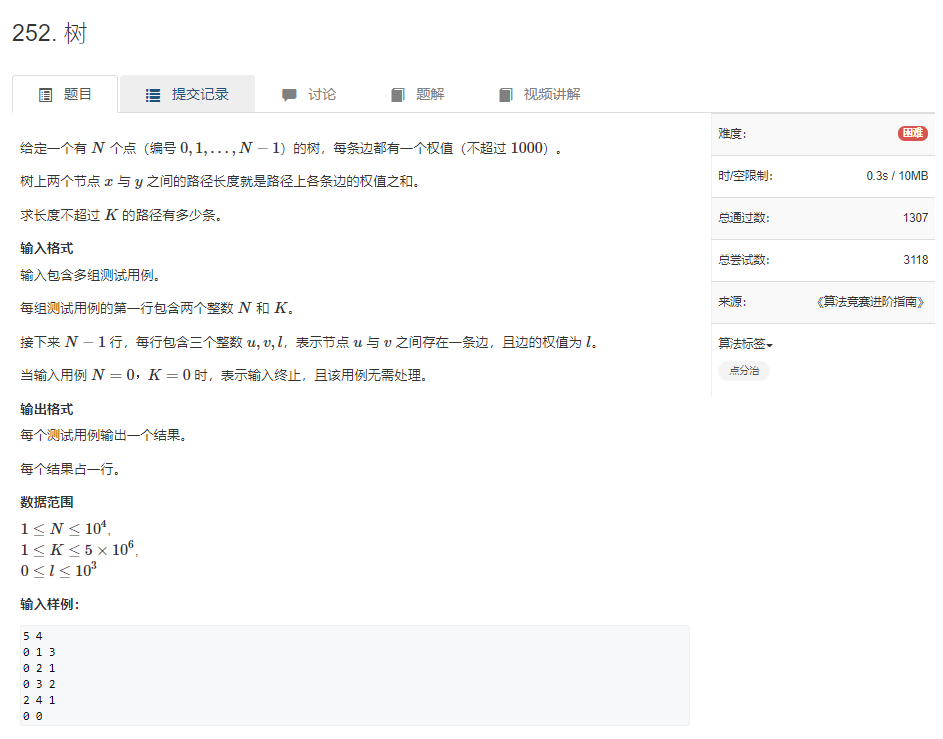
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010, M = N * 2;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
bool st[N];
int p[N], q[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int get_size(int u, int fa) // Find Subtree Size
{
if (st[u]) return 0;
int res = 1;
for (int i = h[u]; ~i; i = ne[i])
if (e[i] != fa)
res += get_size(e[i], u);
return res;
}
int get_wc(int u, int fa, int tot, int& wc) // Center of gravity
{
if (st[u]) return 0;
int sum = 1, ms = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
int t = get_wc(j, u, tot, wc);
ms = max(ms, t);
sum += t;
}
ms = max(ms, tot - sum);
if (ms <= tot / 2) wc = u;
return sum;
}
void get_dist(int u, int fa, int dist, int& qt)
{
if (st[u]) return;
q[qt ++ ] = dist;
for (int i = h[u]; ~i; i = ne[i])
if (e[i] != fa)
get_dist(e[i], u, dist + w[i], qt);
}
int get(int a[], int k)
{
sort(a, a + k);
int res = 0;
for (int i = k - 1, j = -1; i >= 0; i -- )
{
while (j + 1 < i && a[j + 1] + a[i] <= m) j ++ ;
j = min(j, i - 1);
res += j + 1;
}
return res;
}
int calc(int u)
{
if (st[u]) return 0;
int res = 0;
get_wc(u, -1, get_size(u, -1), u);
st[u] = true; // Remove center of gravity
int pt = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i], qt = 0;
get_dist(j, -1, w[i], qt);
res -= get(q, qt);
for (int k = 0; k < qt; k ++ )
{
if (q[k] <= m) res ++ ;
p[pt ++ ] = q[k];
}
}
res += get(p, pt);
for (int i = h[u]; ~i; i = ne[i]) res += calc(e[i]);
return res;
}
int main()
{
while (scanf("%d%d", &n, &m), n || m)
{
memset(st, 0, sizeof st);
memset(h, -1, sizeof h);
idx = 0;
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
printf("%d\n", calc(0));
}
return 0;
}
AcWing 264.Weight
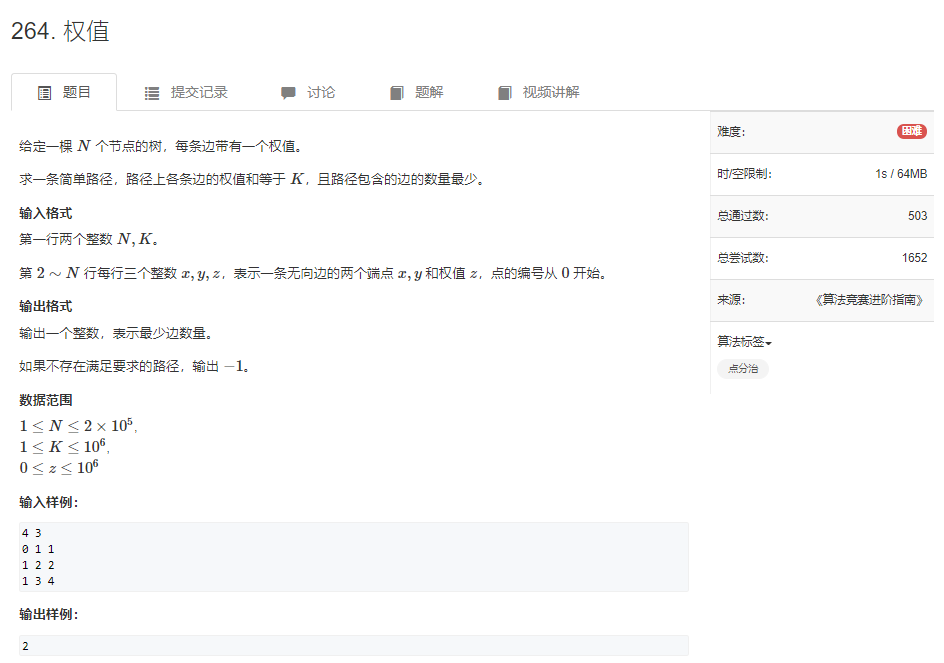
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 200010, M = N * 2, S = 1000010, INF = 0x3f3f3f3f;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
int f[S], ans = INF;
PII p[N], q[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int get_size(int u, int fa)
{
if (st[u]) return 0;
int res = 1;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
res += get_size(j, u);
}
return res;
}
int get_wc(int u, int fa, int tot, int& wc)
{
if (st[u]) return 0;
int sum = 1, ms = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
int t = get_wc(j, u, tot, wc);
ms = max(ms, t);
sum += t;
}
ms = max(ms, tot - sum);
if (ms <= tot / 2) wc = u;
return sum;
}
void get_dist(int u, int fa, int dist, int cnt, int& qt)
{
if (st[u] || dist > m) return;
q[qt ++ ] = {dist, cnt};
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
get_dist(j, u, dist + w[i], cnt + 1, qt);
}
}
void calc(int u)
{
if (st[u]) return;
get_wc(u, -1, get_size(u, -1), u);
st[u] = true;
int pt = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i], qt = 0;
get_dist(j, u, w[i], 1, qt);
for (int k = 0; k < qt; k ++ )
{
auto& t = q[k];
if (t.x == m) ans = min(ans, t.y);
ans = min(ans, f[m - t.x] + t.y);
p[pt ++ ] = t;
}
for (int k = 0; k < qt; k ++ )
{
auto& t = q[k];
f[t.x] = min(f[t.x], t.y);
}
}
for (int i = 0; i < pt; i ++ )
f[p[i].x] = INF;
for (int i = h[u]; ~i; i = ne[i]) calc(e[i]);
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
memset(f, 0x3f, sizeof f);
calc(0);
if (ans == INF) ans = -1;
printf("%d\n", ans);
return 0;
}
Point Tree
AcWing 2226.Open a shop


#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 150010, M = N * 2;
int n, m, A;
int h[N], e[M], w[M], ne[M], idx;
int age[N];
bool st[N];
struct Father
{
int u, num;
LL dist;
};
vector<Father> f[N];
struct Son
{
int age;
LL dist;
bool operator< (const Son& t) const
{
return age < t.age;
}
};
vector<Son> son[N][3];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int get_size(int u, int fa)
{
if (st[u]) return 0;
int res = 1;
for (int i = h[u]; ~i; i = ne[i])
if (e[i] != fa)
res += get_size(e[i], u);
return res;
}
int get_wc(int u, int fa, int tot, int& wc)
{
if (st[u]) return 0;
int sum = 1, ms = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
int t = get_wc(j, u, tot, wc);
ms = max(ms, t);
sum += t;
}
ms = max(ms, tot - sum);
if (ms <= tot / 2) wc = u;
return sum;
}
void get_dist(int u, int fa, LL dist, int wc, int k, vector<Son>& p)
{
if (st[u]) return;
f[u].push_back({wc, k, dist});
p.push_back({age[u], dist});
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
get_dist(j, u, dist + w[i], wc, k, p);
}
}
void calc(int u)
{
if (st[u]) return;
get_wc(u, -1, get_size(u, -1), u);
st[u] = true;
for (int i = h[u], k = 0; ~i; i = ne[i])
{
int j = e[i];
if (st[j]) continue;
auto& p = son[u][k];
p.push_back({-1, 0}), p.push_back({A + 1, 0});
get_dist(j, -1, w[i], u, k, p);
k ++ ;
sort(p.begin(), p.end());
for (int i = 1; i < p.size(); i ++ ) p[i].dist += p[i - 1].dist;
}
for (int i = h[u]; ~i; i = ne[i]) calc(e[i]);
}
LL query(int u, int l, int r)
{
LL res = 0;
for (auto& t: f[u])
{
int g = age[t.u];
if (g >= l && g <= r) res += t.dist;
for (int i = 0; i < 3; i ++ )
{
if (i == t.num) continue;
auto& p = son[t.u][i];
if (p.empty()) continue;
int a = lower_bound(p.begin(), p.end(), Son({l, -1})) - p.begin();
int b = lower_bound(p.begin(), p.end(), Son({r + 1, -1})) - p.begin();
res += t.dist * (b - a) + p[b - 1].dist - p[a - 1].dist;
}
}
for (int i = 0; i < 3; i ++ )
{
auto& p = son[u][i];
if (p.empty()) continue;
int a = lower_bound(p.begin(), p.end(), Son({l, -1})) - p.begin();
int b = lower_bound(p.begin(), p.end(), Son({r + 1, -1})) - p.begin();
res += p[b - 1].dist - p[a - 1].dist;
}
return res;
}
int main()
{
scanf("%d%d%d", &n, &m, &A);
for (int i = 1; i <= n; i ++ ) scanf("%d", &age[i]);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
calc(1);
LL res = 0;
while (m -- )
{
int u, a, b;
scanf("%d%d%d", &u, &a, &b);
int l = (a + res) % A, r = (b + res) % A;
if (l > r) swap(l, r);
res = query(u, l, r);
printf("%lld\n", res);
}
return 0;
}
CDQ Dividing
AcWing 2815.3-D Partial Order
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200010;
int n, m;
struct Data
{
int a, b, c, s, res;
bool operator< (const Data& t) const
{
if (a != t.a) return a < t.a;
if (b != t.b) return b < t.b;
return c < t.c;
}
bool operator== (const Data& t) const
{
return a == t.a && b == t.b && c == t.c;
}
}q[N], w[N];
int tr[M], ans[N];
int lowbit(int x)
{
return x & -x;
}
void add(int x, int v)
{
for (int i = x; i < M; i += lowbit(i)) tr[i] += v;
}
int query(int x)
{
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
void merge_sort(int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(l, mid), merge_sort(mid + 1, r);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
if (q[i].b <= q[j].b) add(q[i].c, q[i].s), w[k ++ ] = q[i ++ ];
else q[j].res += query(q[j].c), w[k ++ ] = q[j ++ ];
while (i <= mid) add(q[i].c, q[i].s), w[k ++ ] = q[i ++ ];
while (j <= r) q[j].res += query(q[j].c), w[k ++ ] = q[j ++ ];
for (i = l; i <= mid; i ++ ) add(q[i].c, -q[i].s);
for (i = l, j = 0; j < k; i ++, j ++ ) q[i] = w[j];
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
q[i] = {a, b, c, 1};
}
sort(q, q + n);
int k = 1;
for (int i = 1; i < n; i ++ )
if (q[i] == q[k - 1]) q[k - 1].s ++ ;
else q[k ++ ] = q[i];
merge_sort(0, k - 1);
for (int i = 0; i < k; i ++ )
ans[q[i].res + q[i].s - 1] += q[i].s;
for (int i = 0; i < n; i ++ ) printf("%d\n", ans[i]);
return 0;
}
AcWing 2847.Old C's Task

/*
*
* The idea is to expand the point to three-dimensional (x, y, z) z 1 to represent the point in the query and Z 0 to represent the point already on the original map.
* Each query corresponds to a two-dimensional difference problem. The key problem is how to find Xi <= x for a coordinate point (x, y)
* And Yi <= y, the weight of all points, plus z, is exactly the same as the point with z=1 (x, y, z). All of
* xi <= x and y1 <= y and zi = 0 The weight of all points, so that it can be converted to a CDQ Division
*
*/
#include <stdio.h>
#include <string.h>
#include <map>
#include <algorithm>
using namespace std;
const int MAX_NODE_NUM = 1000000;
// A tuple representing three dimension attribute values
struct Node {
int a, b; // a, b corresponds to x, y coordinates
int c; // The c value is 0, 1, 0 for points on the original diagram and 1 for points involved in the query
long long sum; // Weights and values of all points with c equal to 0 in the lower left corner of the current point
long long wei; // Point weight
bool operator < (const Node& other) const {
if (a != other.a) return a < other.a;
if (b != other.b) return b < other.b;
return c < other.c;
}
bool operator == (const Node& other) {
return a == other.a && b == other.b && c == other.c;
}
} buf[1000000], merge_buf[1000000], q[1000000]; // BUF is the cache of the input data as well as the result cache, merge_buf is the extra cache used when merging and sorting
void merge_sort(int ll, int rr) {
if (ll == rr) {
return;
}
int mid = (ll + rr) >> 1;
merge_sort(ll, mid);
merge_sort(mid+1, rr);
int ii = ll - 1;
int pos = -1;
long long tot = 0;
for (int jj = mid + 1; jj <= rr; jj++) {
while (ii+1 <= mid && buf[ii+1].b <= buf[jj].b) {
ii += 1;
if (buf[ii].c == 0) {
tot += buf[ii].wei;
}
merge_buf[++pos] = buf[ii];
}
if (buf[jj].c == 1) {
buf[jj].sum += tot;
}
merge_buf[++pos] = buf[jj];
}
while (ii+1 <= mid) {
ii += 1;
merge_buf[++pos] = buf[ii];
}
// Subinterval Combination
for (int i = ll; i <= rr; i++) {
buf[i] = merge_buf[i-ll];
}
}
// n is the length of the input triple array
void cdq(int n) {
sort(buf, buf + n);
merge_sort(0, n-1);
}
int ans[1000000];
int main() {
// freopen("/Users/grh/Programming/CLionProjects/SimpleTest/input.txt", "r", stdin);
int n, m;
int a, b, w;
scanf("%d %d", &n, &m);
int pos = 0;
for (int i = 0; i < n; i++) {
scanf("%d %d %lld", &(buf[pos].a), &(buf[pos].b), &(buf[pos].wei));
buf[pos].c = 0;
buf[pos].sum = 0;
pos += 1;
}
int x1, y1, x2, y2;
int q_pos = 0;
for (int i = 0; i < m; i++) {
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
if (x1 > x2) {
swap(x1, x2);
}
if (y1 > y2) {
swap(y1, y2);
}
buf[pos].a = x2, buf[pos].b = y2, buf[pos].c = 1;
buf[pos].wei = 0, buf[pos].sum = 0;
q[q_pos++] = buf[pos];
pos += 1;
buf[pos].a = x1-1, buf[pos].b = y2, buf[pos].c = 1;
buf[pos].wei = 0, buf[pos].sum = 0;
q[q_pos++] = buf[pos];
pos += 1;
buf[pos].a = x2, buf[pos].b = y1-1, buf[pos].c = 1;
buf[pos].wei = 0, buf[pos].sum = 0;
q[q_pos++] = buf[pos];
pos += 1;
buf[pos].a = x1-1, buf[pos].b = y1-1, buf[pos].c = 1;
buf[pos].wei = 0, buf[pos].sum = 0;
q[q_pos++] = buf[pos];
pos += 1;
}
cdq(pos);
map<Node, long long> nodes;
for (int i = 0; i < pos; i++) {
if (buf[i].c == 1) {
nodes[buf[i]] = buf[i].sum;
}
}
// Differential calculation using four key points of a rectangle
for (int i = 0; i < q_pos >> 2; i++) {
long long tot = 0;
tot += nodes[q[i * 4]];
tot -= nodes[q[i * 4 + 1]];
tot -= nodes[q[i * 4 + 2]];
tot += nodes[q[i * 4 + 3]];
printf("%lld\n", tot);
}
return 0;
}
AcWing 2819.Dynamic Reverse Order Pair
/*
*
* Construct three attributes. The three-dimensional partial order problem is solved by CDQ division algorithm. Attribute a is the weight of the point, that is, the value from 1 to N, attribute b is the subscript of the point, and attribute c is the point at which the point was deleted. Set the first one
* The deletion time of deleted points is N, and the deletion time of subsequently deleted points decreases in turn (deletion time of points without deletion is randomly divided from the remaining points)
*
* Assuming that the point whose deletion time is I and the point whose deletion time is j constitute an inverse order pair (i,j), then (j, i) is also an inverse order pair, but the two inverse order pairs can only be counted once, the uniform rule is to accumulate the count to I
* j The larger of the middle, that I s, the earlier deleted point, the definition s[i] means the inverse pair counts that are accumulated at the point where the deletion time i s I. Under such a specially constructed definition, the problem requires the deletion
* The inverse logarithmic number before a point'(assuming the point deletion time i s i), i s s[i] + s[i-1] + s[i-2] +.....S[1], i s a prefix sum, so just consider how to find s[i]
*
* Nodes with deletion time i may have two reverse pairs (where i is the c attribute in the node):
*
* First, the value of node(i) is small, and point j with a larger value deleted later is paired in reverse order, contributing to the I node:
* node(j).a > node(i).a && node(j).b < node(i).b && node(j).c < node(i).c
*
* Second, the node(i) has a larger value and a smaller point j deleted later is paired in reverse order, contributing to the I node:
* node(j).a < node(i).a && node(j).b > node(i).b && node(j).c < node(i).c
*
* (The two types of reverse order are also okay for swapping roles, and the problem is symmetrical or the same)
*
* For these two types of reverse order pairs, each node is given all the two types of reverse order pairs that can be constructed, and the contribution values are accumulated at the corresponding locations. All reverse order pairs are not missed.
* So the problem becomes two separate three-dimensional partial ordering problems (greater than sign in the problem, the opposite number of the original attribute can become less than sign), solve them separately, and prefix them again
* And, for each query, print out the corresponding prefix and
*
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_FENWICK_LEN = 100005;
int sum_seg[MAX_FENWICK_LEN];
class FenwickTree {
private:
int data_len; // Length of stored prefixes and sums
// Gets the prefix and sum of the intervals [0, end]
int __get_sum_with_end(int end) {
int ans = 0;
while (end) {
ans += sum_seg[end];
end &= (end - 1);
}
return ans;
}
public:
FenwickTree(int n) : data_len(n) {
for (int i = 1; i <= n; i++) {
sum_seg[i] = 0;
}
}
// Get the original value at x
int get_orig_val(int x) {
x += 1;
if (x < 1 || x > data_len) {
// Exception Branch
return 0;
}
int ans = sum_seg[x];
int lca = x & (x-1);
x--;
while (x != lca) {
ans -= sum_seg[x];
x &= (x-1);
}
return ans;
}
// Gets the prefix and sum of the interval [start, end]
int get_sum(int start, int end) {
start++, end++;
if (! (end >= start && start >= 1 && end <= data_len)) {
// Exception Branch
return 0;
}
if (start == 1) {
return __get_sum_with_end(end);
}
return __get_sum_with_end(end) - __get_sum_with_end(start - 1);
}
// The original sequence value at x position increases delta
void add_val(int x, int delta) {
x += 1;
while (x <= data_len) {
sum_seg[x] += delta;
x += x & (-x);
}
}
};
const int MAX_NODE_NUM = 100005;
// A tuple representing three dimension attribute values
struct Node {
int a, b, c; // Attribute values for three dimensions
int cnt; // Number of nodes in the original sequence whose values are equal to (a, b, c)
int le_num; // For point X in the original sequence with numeric value equal to (a, b, c), the 3-D partial order is less than the number of primitive nodes equal to X (excluding the X node itself)
bool operator < (const Node& other) const {
if (a != other.a) return a < other.a;
if (b != other.b) return b < other.b;
return c < other.c;
}
bool operator == (const Node& other) {
return a == other.a && b == other.b && c == other.c;
}
} buf[MAX_NODE_NUM], buf1[MAX_NODE_NUM], buf2[MAX_NODE_NUM], merge_buf[MAX_NODE_NUM]; // BUF is the cache of the input data as well as the result cache, merge_buf is the extra cache used when merging and sorting
// Divide and conquer resolves problems within [ll, rr] intervals, sorting by merge based on b attribute
FenwickTree fenwick(100005 + 10);
// s[i] denotes and deletes that the timestamp i s the inverse logarithm of the numeric pairing of I
long long s[MAX_NODE_NUM];
void merge_sort(int ll, int rr) {
if (ll == rr) {
return;
}
int mid = (ll + rr) >> 1;
merge_sort(ll, mid);
merge_sort(mid+1, rr);
int ii = ll - 1;
int pos = -1;
for (int jj = mid + 1; jj <= rr; jj++) {
while (ii+1 <= mid && buf[ii+1].b <= buf[jj].b) {
ii += 1;
fenwick.add_val(buf[ii].c, buf[ii].cnt);
merge_buf[++pos] = buf[ii];
}
int sum_val = fenwick.get_sum(0, buf[jj].c);
s[buf[jj].c] += sum_val;
buf[jj].le_num += sum_val;
merge_buf[++pos] = buf[jj];
}
// Restore the tree array back
for (int i = ll; i <= ii; i++) {
fenwick.add_val(buf[i].c, -buf[i].cnt);
}
while (ii+1 <= mid) {
ii += 1;
merge_buf[++pos] = buf[ii];
}
// Subinterval Combination
for (int i = ll; i <= rr; i++) {
buf[i] = merge_buf[i-ll];
}
}
// n is the length of the input triple array
void cdq(int n) {
sort(buf, buf + n);
merge_sort(0, n-1);
}
// Mapping of values to Subscripts
int val2idx[MAX_NODE_NUM];
int main(void) {
int n, m;
scanf("%d %d", &n, &m);
int val;
for (int i = 0; i < n; i++) {
scanf("%d", &val);
val2idx[val] = i;
buf1[i].a = val;
buf1[i].b = i;
buf1[i].c = 0;
buf1[i].cnt = 1;
}
for (int i = 0; i < m; i++) {
scanf("%d", &val);
buf1[val2idx[val]].c = n - i;
}
int rank = n-m;
for (int i = 0; i < n; i++) {
if (buf1[i].c == 0) {
buf1[i].c = rank--;
}
}
for (int i = 0; i < n; i++) {
buf[i] = buf1[i];
buf[i].a = n+1 - buf1[i].a;
}
cdq(n);
for (int i = 0; i < n; i++) {
buf[i] = buf1[i];
buf[i].b = n+1 - buf1[i].b;
}
cdq(n);
// s sums the prefix
for (int i = 1; i <= n; i++) {
s[i] += s[i-1];
}
for (int i = n; i > n-m; i--) {
printf("%lld\n", s[i]);
}
return 0;
}
Author: Keep your head open
Links: https://www.acwing.com/solution/content/50059/
Source: AcWing
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.
- Construct three attributes. The three-dimensional partial order problem is solved by CDQ division algorithm. Attribute a is the weight of the point, that is, the value from 1 to N, attribute b is the subscript of the point, and attribute c is the point at which the point was deleted. Set the first one
- The deletion time of deleted points is N, and the deletion time of subsequently deleted points decreases in turn (deletion time of points without deletion is randomly divided from the remaining points)
- Assuming that the point whose deletion time is I and the point whose deletion time is j constitute an inverse order pair (i,j), then (j, i) is also an inverse order pair, but the two inverse order pairs can only be counted once, the uniform rule is to accumulate the count to I
- The larger point in j, that I s, the earlier deleted point, defines s[i] as an inverse pair count that i s accumulated at the point where the deletion time i s I. Under such a specially constructed definition, the problem requires a "delete"
- The inverse logarithmic number before a point'(assuming the point deletion time i s i) i s s[i] + s[i-1] + s[i-2] +...s[1], which i s a prefix sum, so just consider how s[i]
- Nodes with deletion time i may have two reverse pairs (where i is the c attribute in the node):
- First, the value of node(i) is small, and point j with a larger value deleted later is paired in reverse order, contributing to the I node:
- node(j).a > node(i).a && node(j).b < node(i).b && node(j).c < node(i).c
- Second, the node(i) has a larger value and a smaller point j deleted later is paired in reverse order, contributing to the I node:
- node(j).a < node(i).a && node(j).b > node(i).b && node(j).c < node(i).c
- (The two types of reverse order are also okay for swapping roles, and the symmetrical problem is the same)
- For these two types of reverse order pairs, each node is given all the two types of reverse order pairs that can be constructed, and the contribution values are accumulated at the corresponding locations. All reverse order pairs are not missed.
- So the problem becomes two separate three-dimensional partial ordering problems (greater than sign in the problem, the opposite number of the original attribute can become less than sign), solve them separately, and prefix them again
- And, for each query, print out the corresponding prefix and
Cactus
AcWing 2863.shortest path
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 12010, M = N * 3;
int n, m, Q, new_n;
int h1[N], h2[N], e[M], w[M], ne[M], idx;
int dfn[N], low[N], cnt;
int s[N], stot[N], fu[N], fw[N];
int fa[N][14], depth[N], d[N];
int A, B;
void add(int h[], int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void build_circle(int x, int y, int z)
{
int sum = z;
for (int k = y; k != x; k = fu[k])
{
s[k] = sum;
sum += fw[k];
}
s[x] = stot[x] = sum;
add(h2, x, ++ new_n, 0);
for (int k = y; k != x; k = fu[k])
{
stot[k] = sum;
add(h2, new_n, k, min(s[k], sum - s[k]));
}
}
void tarjan(int u, int from)
{
dfn[u] = low[u] = ++ cnt;
for (int i = h1[u]; ~i; i = ne[i])
{
int j = e[i];
if (!dfn[j])
{
fu[j] = u, fw[j] = w[i];
tarjan(j, i);
low[u] = min(low[u], low[j]);
if (dfn[u] < low[j]) add(h2, u, j, w[i]);
}
else if (i != (from ^ 1)) low[u] = min(low[u], dfn[j]);
}
for (int i = h1[u]; ~i; i = ne[i])
{
int j = e[i];
if (dfn[u] < dfn[j] && fu[j] != u)
build_circle(u, j, w[i]);
}
}
void dfs_lca(int u, int father)
{
depth[u] = depth[father] + 1;
fa[u][0] = father;
for (int k = 1; k <= 13; k ++ )
fa[u][k] = fa[fa[u][k - 1]][k - 1];
for (int i = h2[u]; ~i; i = ne[i])
{
int j = e[i];
d[j] = d[u] + w[i];
dfs_lca(j, u);
}
}
int lca(int a, int b)
{
if (depth[a] < depth[b]) swap(a, b);
for (int k = 13; k >= 0; k -- )
if (depth[fa[a][k]] >= depth[b])
a = fa[a][k];
if (a == b) return a;
for (int k = 13; k >= 0; k -- )
if (fa[a][k] != fa[b][k])
{
a = fa[a][k];
b = fa[b][k];
}
A = a, B = b;
return fa[a][0];
}
int main()
{
scanf("%d%d%d", &n, &m, &Q);
new_n = n;
memset(h1, -1, sizeof h1);
memset(h2, -1, sizeof h2);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(h1, a, b, c), add(h1, b, a, c);
}
tarjan(1, -1);
dfs_lca(1, 0);
while (Q -- )
{
int a, b;
scanf("%d%d", &a, &b);
int p = lca(a, b);
if (p <= n) printf("%d\n", d[a] + d[b] - d[p] * 2);
else
{
int da = d[a] - d[A], db = d[b] - d[B];
int l = abs(s[A] - s[B]);
int dm = min(l, stot[A] - l);
printf("%d\n", da + dm + db);
}
}
return 0;
}
AcWing 2752.cactus
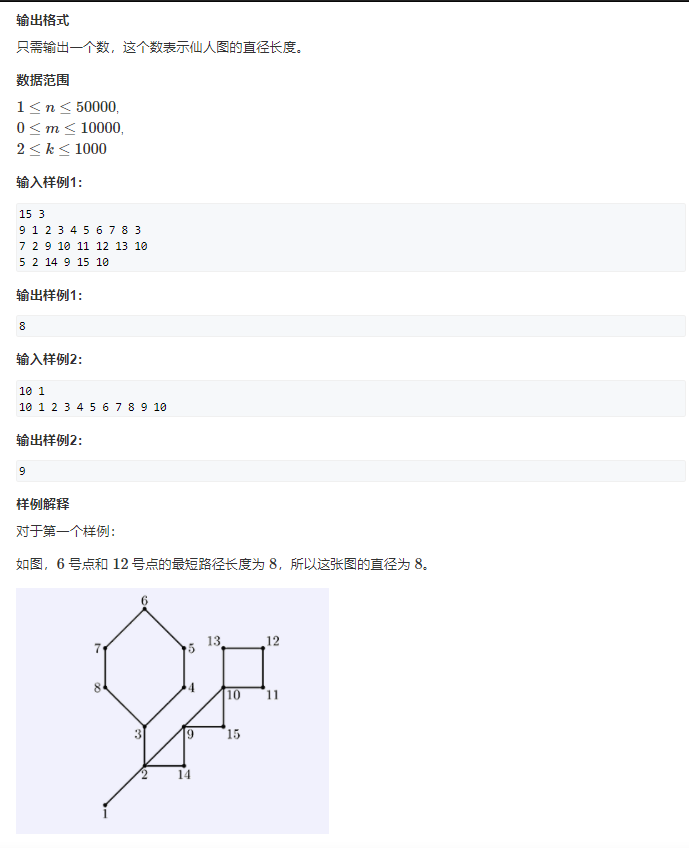
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = N * 3, INF = 1e8;
int n, m, new_n;
int h1[N], h2[N], e[M], w[M], ne[M], idx;
int dfn[N], low[N], cnt;
int s[N], stot[N], fu[N], fw[N];
int d[N], f[N], q[N];
int ans;
void add(int h[], int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void build_circle(int x, int y, int z)
{
int sum = z;
for (int k = y; k != x; k = fu[k])
{
s[k] = sum;
sum += fw[k];
}
s[x] = stot[x] = sum;
add(h2, x, ++ new_n, 0);
for (int k = y; k != x; k = fu[k])
{
stot[k] = sum;
add(h2, new_n, k, min(s[k], sum - s[k]));
}
}
void tarjan(int u, int from)
{
dfn[u] = low[u] = ++ cnt;
for (int i = h1[u]; ~i; i = ne[i])
{
int j = e[i];
if (!dfn[j])
{
fu[j] = u, fw[j] = w[i];
tarjan(j, i);
low[u] = min(low[u], low[j]);
if (dfn[u] < low[j]) add(h2, u, j, w[i]);
}
else if (i != (from ^ 1)) low[u] = min(low[u], dfn[j]);
}
for (int i = h1[u]; ~i; i = ne[i])
{
int j = e[i];
if (dfn[u] < dfn[j] && fu[j] != u)
build_circle(u, j, w[i]);
}
}
int dfs(int u)
{
int d1 = 0, d2 = 0;
for (int i = h2[u]; ~i; i = ne[i])
{
int j = e[i];
int t = dfs(j) + w[i];
if (t >= d1) d2 = d1, d1 = t;
else if (t > d2) d2 = t;
}
f[u] = d1;
if (u <= n) ans = max(ans, d1 + d2); // u is a dot
else // u is a square point
{
int sz = 0;
d[sz ++ ] = -INF;
for (int i = h2[u]; ~i; i = ne[i])
d[sz ++ ] = f[e[i]];
for (int i = 0; i < sz; i ++ ) d[sz + i] = d[i];
int hh = 0, tt = -1;
for (int i = 0; i < sz * 2; i ++ )
{
if (hh <= tt && i - q[hh] > sz / 2) hh ++ ;
if (hh <= tt) ans = max(ans, d[i] + i + d[q[hh]] - q[hh]);
while (hh <= tt && d[q[tt]] - q[tt] <= d[i] - i) tt -- ;
q[ ++ tt] = i;
}
}
return f[u];
}
int main()
{
scanf("%d%d", &n, &m);
new_n = n;
memset(h1, -1, sizeof h1);
memset(h2, -1, sizeof h2);
while (m -- )
{
int k, x, y;
scanf("%d%d", &k, &x);
for (int i = 0; i < k - 1; i ++ )
{
scanf("%d", &y);
add(h1, x, y, 1), add(h1, y, x, 1);
x = y;
}
}
tarjan(1, -1);
dfs(1);
printf("%d\n", ans);
return 0;
}