Knowledge point 01: Nine sorting algorithms

public class Sort {
    public static void main(String[] args) {
        testTime();
        testSort();
    }

    public static void testTime() {
        int[] arr = new int[10000];
        for (int i = 0; i < 10000; i++) {
            arr[i] = (int) (Math.random() * 100 + 1);
        }
        long s = System.currentTimeMillis();
//        bubbleSort(arr);
//        selectionSort(arr);
//        insertionSort(arr);
//        shellSort(arr);
//        quickSort(arr, 0, arr.length - 1);
//        mergeSort(arr, 0, arr.length - 1, new int[arr.length]);
//        radixSort(arr);
//        countingSort(arr);
//        heapSort(arr);
        long e = System.currentTimeMillis();
        System.out.println((e - s) + "ms");
    }

    public static void testSort() {
        int[] arr = new int[50];
        for (int i = 0; i < 50; i++) {
            arr[i] = (int) (Math.random() * 100 + 1);
        }
//        bubbleSort(arr);
//        selectionSort(arr);
//        insertionSort(arr);
//        shellSort(arr);
//        quickSort(arr, 0, arr.length - 1);
//        mergeSort(arr, 0, arr.length - 1, new int[arr.length]);
//        radixSort(arr);
//        countingSort(arr);
//        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    //Heap sorting (large top heap: ascending algorithm, small top heap: descending algorithm)
    public static void heapSort(int arr[]) {
        //Create large top heap
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            heapAdjust(arr, i, arr.length);
        }
        //Adjust the large top reactor
        for (int i = arr.length - 1; i > 0; i--) {
            //Exchange element
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;
            //Adjust new heap
            heapAdjust(arr, 0, i);
        }
    }

    //Heap adjustment
    public static void heapAdjust(int arr[], int ci, int length) {
        //Cache current node
        int temp = arr[ci];
        //Start cycle adjustment
        for (int li = ci * 2 + 1; li < length; li = li * 2 + 1) {
            //It indicates that the value of the left child node is less than that of the right child node
            if (li + 1 < length && arr[li] < arr[li + 1]) {
                li = li + 1;
            }
            //Indicates that the value of the current child node is greater than that of the parent node
            if (arr[li] > temp) {
                arr[ci] = arr[li];
                ci = li;
            } else {
                break;
            }
        }
        //Place in the adjustment position
        arr[ci] = temp;
    }

    //Count sorting: ascending algorithm
    public static void countingSort(int[] arr) {
        if (arr == null || arr.length == 0) return;
        int max = arr[0];
        int min = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) max = arr[i];
            if (arr[i] < min) min = arr[i];
        }
        //Statistical times
        int[] counts = new int[max - min + 1];
        for (int i = 0; i < arr.length; i++) {
            counts[arr[i] - min]++;
        }
        //accumulative frequency
        for (int i = 1; i < counts.length; i++) {
            counts[i] += counts[i - 1];
        }
        //Reverse rearrangement
        int[] newArr = new int[arr.length];
        for (int i = arr.length - 1; i >= 0; i--) {
            newArr[--counts[arr[i] - min]] = arr[i];
        }
        //Copy array
        for (int i = 0; i < arr.length; i++) {
            arr[i] = newArr[i];
        }
    }

    //Cardinality sorting: ascending algorithm
    public static void radixSort(int[] arr) {
        if (arr == null || arr.length == 0) return;
        int max = arr[0];
        int min = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) max = arr[i];
            if (arr[i] < min) min = arr[i];
        }
        for (int i = 0; i < arr.length; i++) {
            arr[i] -= min;
        }
        int maxLength = String.valueOf(max - min).length();
        int[][] bucket = new int[10][arr.length];
        int[] bucketIndex = new int[10];
        for (int rounds = 0, base = 1; rounds < maxLength; rounds++, base *= 10) {
            for (int i = 0; i < arr.length; i++) {
                int digit = arr[i] / base % 10;
                bucket[digit][bucketIndex[digit]++] = arr[i];
            }
            int pos = 0;
            for (int i = 0; i < bucketIndex.length; i++) {
                for (int j = 0; j < bucketIndex[i]; j++) {
                    arr[pos++] = bucket[i][j];
                }
                bucketIndex[i] = 0;
            }
        }
        for (int i = 0; i < arr.length; i++) {
            arr[i] += min;
        }
    }

    //Merge sort: ascending algorithm
    public static void mergeSort(int[] arr, int L, int R, int[] temp) {
        if (L >= R) return;
        int tIdx = L, left = L, middle = (L + R) / 2, right = middle + 1;
        mergeSort(arr, L, middle, temp);
        mergeSort(arr, right, R, temp);
        while (left <= middle && right <= R) {
            if (arr[left] <= arr[right]) {
                temp[tIdx++] = arr[left++];
            } else {
                temp[tIdx++] = arr[right++];
            }
        }
        while (left <= middle) temp[tIdx++] = arr[left++];
        while (right <= R) temp[tIdx++] = arr[right++];
        for (int i = L; i <= R; i++) {
            arr[i] = temp[i];
        }
    }

    //Quick sort: ascending algorithm
    public static void quickSort(int[] arr, int L, int R) {
        if (L >= R) return;
        int left = L, right = R, pivot = arr[L];
        while (left < right) {
            while (left < right && arr[right] >= pivot) right--;
            arr[left] = arr[right];
            while (left < right && arr[left] <= pivot) left++;
            arr[right] = arr[left];
        }
        arr[left] = pivot;
        quickSort(arr, L, left - 1);
        quickSort(arr, left + 1, R);
    }

    //Hill sorting: ascending algorithm
    public static void shellSort(int[] arr) {
        for (int step = arr.length / 2; step > 0; step /= 2) {
            for (int i = step; i < arr.length; i++) {
                int temp = arr[i];
                int j = i - step;
                while (j >= 0 && arr[j] > temp) {
                    arr[j + step] = arr[j];
                    j -= step;
                }
                arr[j + step] = temp;
            }
        }
    }

    //Insert sort: ascending algorithm
    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int temp = arr[i];
            int j = i - 1;
            while (j >= 0 && arr[j] > temp) {
                arr[j + 1] = arr[j];
                j -= 1;
            }
            arr[j + 1] = temp;
        }
    }

    //Select Sorting: ascending algorithm
    public static void selectionSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[minIndex] > arr[j]) {
                    minIndex = j;
                }
            }
            if (minIndex != i) {
                int temp = arr[minIndex];
                arr[minIndex] = arr[i];
                arr[i] = temp;
            }
        }
    }

    //Bubble sorting: ascending algorithm
    public static void bubbleSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }
}

Knowledge point 02: binary search algorithm

Recursive version:

public static int binarySearch(int[] arr, int target) {
    return binarySearch(arr, 0, arr.length - 1, target);
}

private static int binarySearch(int[] arr, int left, int right, int target) {
    while (left <= right) {
        int middle = (left + right) / 2;
        if (target < arr[middle]) {
            right = middle - 1;
        } else if (target > arr[middle]) {
            left = middle + 1;
        } else {
            return middle;
        }
    }
    return -1;
}

Iteration:

public static int binarySearch(int[] arr, int target) {
    return binarySearch(arr, 0, arr.length - 1, target);
}

private static int binarySearch(int[] arr, int left, int right, int target) {
    if (left > right) return -1;
    int middle = (left + right) / 2;
    if (target < arr[middle]) {
        return binarySearch(arr, left, middle - 1, target);
    } else if (target > arr[middle]) {
        return binarySearch(arr, middle + 1, right, target);
    } else {
        return middle;
    }
}

Knowledge point 03: traversal of binary tree

Tree node:

class TreeNode {
    int data;
    TreeNode left;
    TreeNode right;

    public TreeNode() {}

    public TreeNode(int data) {
        this.data = data;
    }
}

Recursive version:

//Middle left and right
public static void preOrder(TreeNode root) {
    if (root == null) return;
    System.out.print(root.data + " ");
    preOrder(root.left);
    preOrder(root.right);
}

//Left middle right
public static void midOrder(TreeNode root) {
    if (root == null) return;
    midOrder(root.left);
    System.out.print(root.data + " ");
    midOrder(root.right);
}

//Zuo Youzhong
public static void postOrder(TreeNode root) {
    if (root == null) return;
    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.data + " ");
}

Iteration:

//Middle left and right = > right left (hollow)
public static void preOrder(TreeNode root) {
    if (root == null) return;
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node != null) {
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
            stack.push(node);
            stack.push(null);
        } else {
            node = stack.pop();
            System.out.print(node.data + " ");
        }
    }
}

//Left middle right = > right (hollow)
public static void midOrder(TreeNode root) {
    if (root == null) return;
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node != null) {
            if (node.right != null) stack.push(node.right);
            stack.push(node);
            stack.push(null);
            if (node.left != null) stack.push(node.left);
        } else {
            node = stack.pop();
            System.out.print(node.data + " ");
        }
    }
}

//Left and right middle = > (hollow) right and left
public static void postOrder(TreeNode root) {
    if (root == null) return;
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node != null) {
            stack.push(node);
            stack.push(null);
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        } else {
            node = stack.pop();
            System.out.print(node.data + " ");
        }
    }
}

Sequence traversal:

public static void layerOrder(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        System.out.print(node.data + " ");
        if (node.left != null) queue.offer(node.left);
        if (node.right != null) queue.offer(node.right);
    }
}

Knowledge point 04: Spring IOC

Execution process:

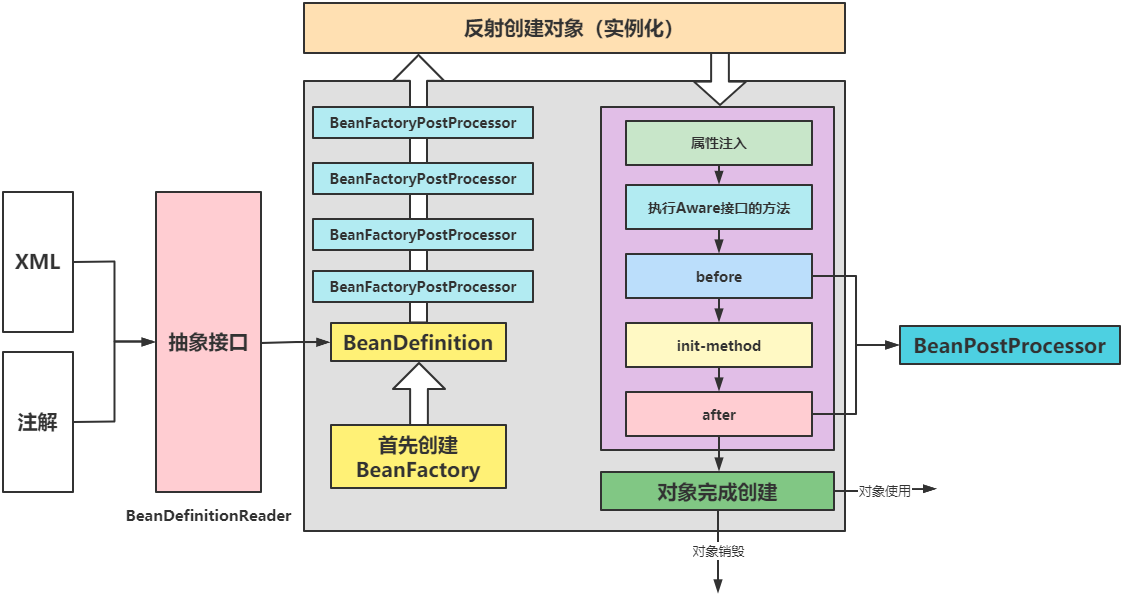
Life cycle:

Circular dependency:

name	Complete definition	Storage type
L1 cache	private final Map<String, Object> singletonObjects = new ConcurrentHashMap<>(256);	Finished product object
L2 cache	private final Map<String, Object> earlySingletonObjects = new ConcurrentHashMap<>(16);	Semi finished product object
L3 cache	private final Map<String, ObjectFactory<?>> singletonFactories = new HashMap<>(16);	lambda expressions

1. If there is only one level cache, can we solve the problem of circular dependency?

If there is only one level cache, it means that both finished objects and semi-finished objects should be placed in the first level cache. When obtaining objects, it is possible to obtain semi-finished objects, which cannot be used directly. Therefore, it is necessary to use the first level cache to store finished objects and the second level cache to store semi-finished objects.

2. Can only L1 and L2 cache solve the problem of circular dependency?

Only the L1 and L2 caches can solve the circular dependency problem, but there are preconditions. The premise is that AOP is not used. If AOP is enabled, Spring will create proxy objects. If there is a circular dependency problem of proxy objects, it still exists.

3. Then the question comes again. Why do you need L3 cache?

The purpose of L3 cache is to solve the problem of circular dependency in the process of proxy.

4. Use the code to demonstrate the whole process of circular dependency execution?

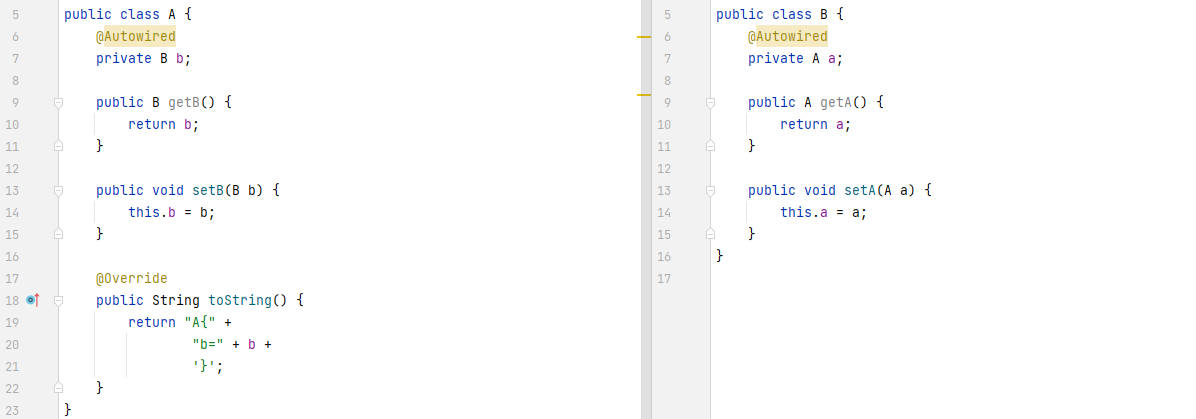
<bean id="a" class="io.github.caochenlei.domain.A">
    <property name="b" ref="b"></property>
</bean>

<bean id="b" class="io.github.caochenlei.domain.B">
    <property name="a" ref="a"></property>
</bean>

public class ABTest {
    public static void main(String[] args) {
        ApplicationContext applicationContext = new ClassPathXmlApplicationContext("ab.xml");
        A a = applicationContext.getBean(A.class);
        System.out.println(a);
        B b = applicationContext.getBean(B.class);
        System.out.println(b);
    }
}

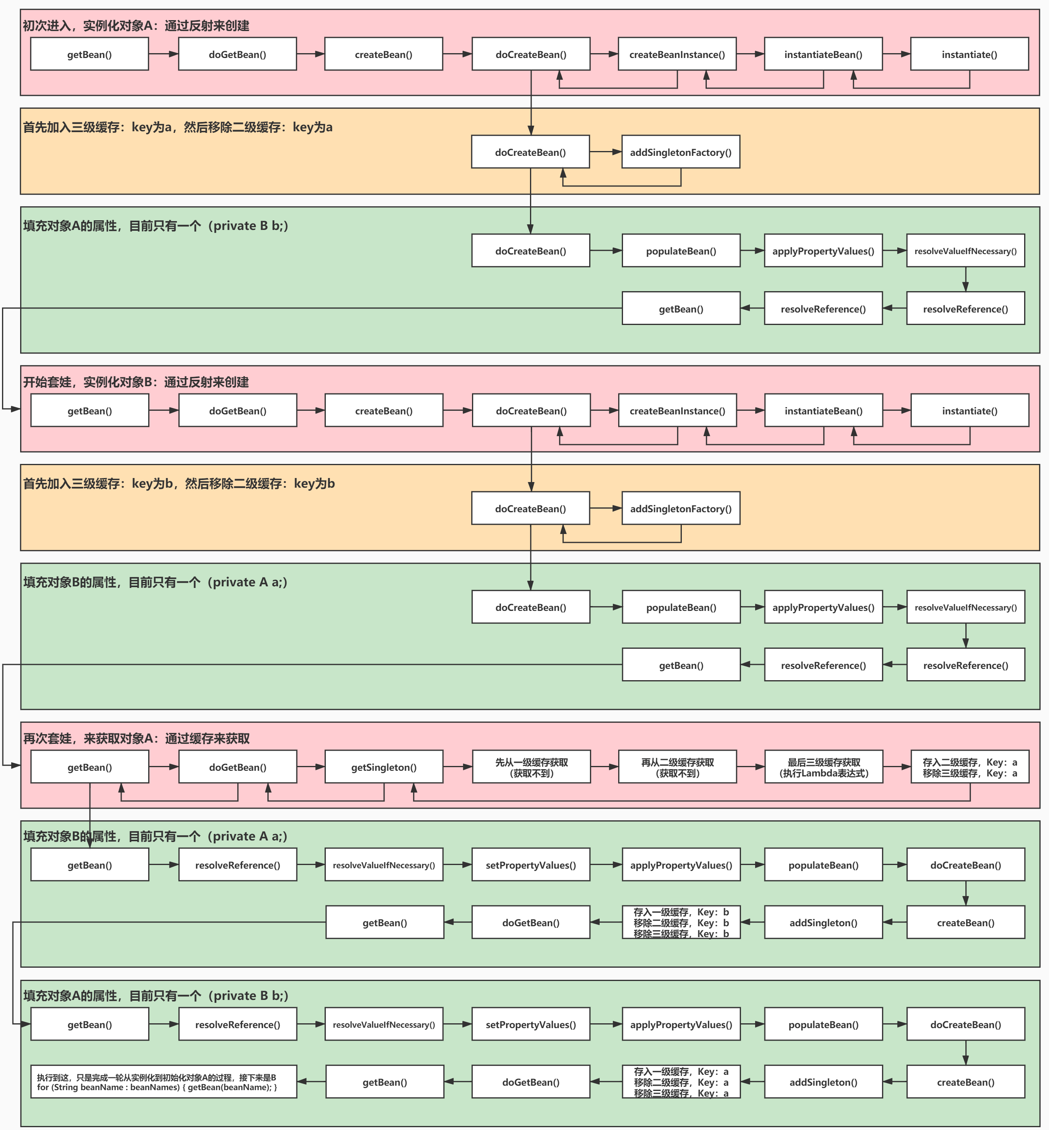
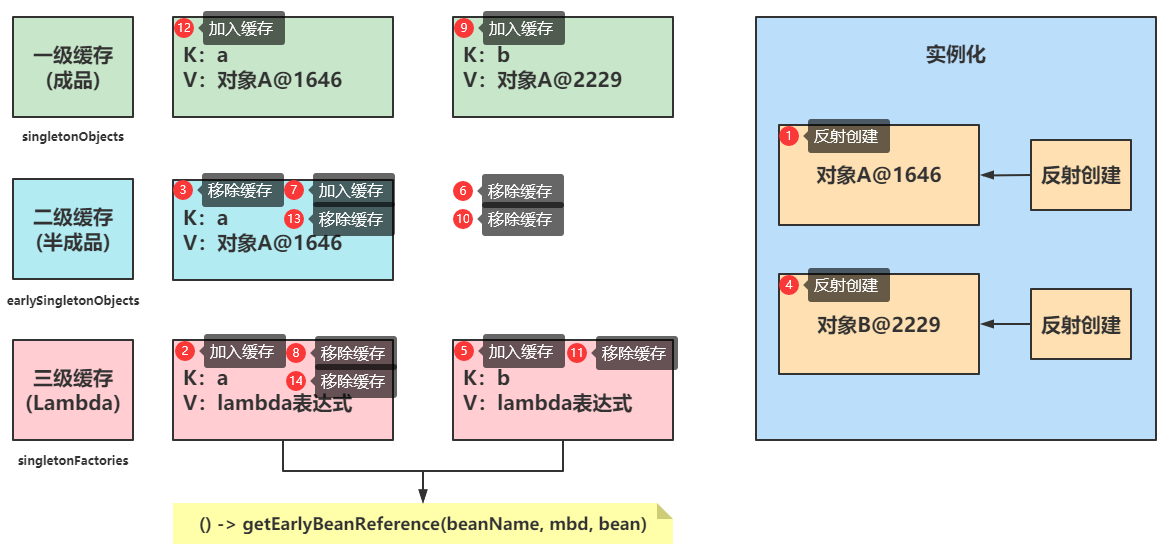
Knowledge point 05: Spring AOP

Not updated yet

Knowledge point 06: TCP triple handshake

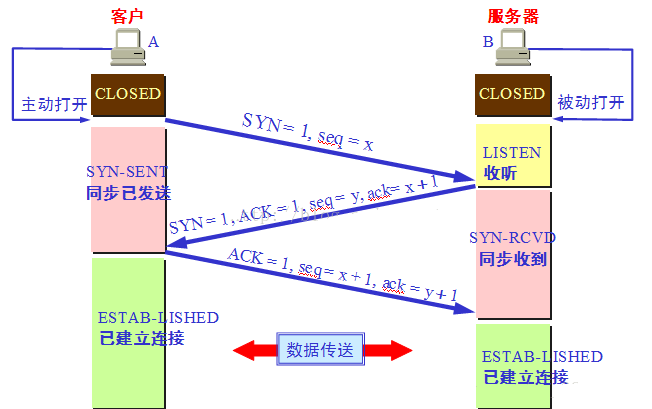
• First handshake: at first, both ends are CLOSED. The Client sets the flag SYN to 1, randomly generates a value seq=x, and sends the packet to the Server. The Client enters the SYN-SENT state and waits for the Server to confirm;
• The second handshake: after the Server receives the data packet, the flag bit SYN=1 knows that the Client requests to establish a connection. The Server sets the flag bits SYN and ack to 1, ack=x+1, randomly generates a value seq=y, and sends the data packet to the Client to confirm the connection request. The Server enters the SYN-RCVD state. At this time, the operating system allocates TCP cache and variables for the TCP connection;
• The third Handshake: after receiving the confirmation, the Client checks whether the ACK is x+1 and the ACK is 1. If it is correct, set the flag bit ack to 1 and ack=y+1. At this time, the operating system allocates TCP cache and variables for the TCP connection and sends the data packet to the Server. The Server checks whether the ACK is y+1 and ACK is 1. If it is correct, the connection is ESTABLISHED successfully, The Client and Server enter the ESTABLISHED state, complete the handshake three times, and then the Client and Server can start transmitting data.

Knowledge point 07: TCP wave four times

• Waving for the first time: the application process of A sends A connection release message segment (FIN=1, sequence number seq=u) to its TCP, stops sending data again, actively closes the TCP connection, enters the FIN-WAIT-1 state, and waits for the confirmation of B.
• Second wave: after receiving the connection release message segment, B sends A confirmation message segment (ACK=1, seq=v, ack=u+1). B enters the CLOSE-WAIT state. At this time, TCP is in the semi closed state and the connection from A to B is released. After receiving the confirmation from B, A enters the FIN-WAIT-2 state and waits for the connection release message segment sent by B.
• The third wave: B has no data to send to A, B sends the connection release message segment (FIN=1, ACK=1, seq=w, ack=u+1), B enters the LAST-ACK state and waits for A's confirmation.
• The fourth wave: after receiving the connection release message segment from B, A sends A confirmation message segment (ACK=1, seq=u+1, ack=w+1), and A enters the TIME-WAIT state. At this time, TCP is not released, and A enters the CLOSED state after the time 2MSL set by the time waiting timer.