Air return problem of school bus transportation
Record the code solution of problem A in the mathematical modeling competition of "University of Technology Press" in 2021
background
Every day, some teachers and staff of a school take a bus from the old campus to the new campus to work. After work, most people will return. The logistics group will arrange vehicles to run back and forth between new and old campuses every day. However, in some periods, the number of people who need to take the bus in the new and old campuses is uneven. For example, in the morning, the teaching staff in the old campus mainly take the bus to the new campus, and in the noon and afternoon after work, the teaching staff mainly return to the new campus from the old campus. Due to the limited vehicles, sometimes in order to meet the needs of vehicles in the current campus, it is necessary to dispatch empty vehicles from another campus (called empty return). How to minimize the number of empty vehicles is a matter of great concern to the logistics group.
The running schedule of the school bus is as follows:
1, Monday to Friday
-
Old campus to new campus
7:00,8:00,9:20,10:00,11:00,12:00,12:50,14:00,14:50,16:00,17:00,17:50,21:00,22:30. -
New campus to old campus
9:00,10:30,11:00,12:30,14:00,15:00,16:00,17:10,18:00,19:00,21:00,22:30.
2, Saturday, Sunday -
Old campus to new campus
8:00,9:20,12:50,14:00,18:00,20:00. -
New campus to old campus
9:00, 11:00,12:30,17:00,18:00,21:00.The running time of vehicles in the two campuses is about one hour. For simplicity, it is assumed that the time for each vehicle to travel from one campus to another is one hour. Due to the unbalanced demand for vehicles at different times in the two campuses, when a campus needs a large number of vehicles and the existing vehicles can not meet the demand, it is necessary to dispatch empty vehicles from another campus. The empty train can start at a certain time in the existing departure schedule, or one hour in advance when necessary.
The school has a total of 20 vehicles, each of which can carry 47 guests. Please build a mathematical model and carefully consider the following problems.
Model overview
This problem is an integer programming model. The decision variables are the actual number of buses at all departure times and the number of school buses at the two campuses at the initial time. The objective function is the number of empty returns, which is actually the actual number of departures minus the target number of departures. Then sum each moment.
subject
Question 1
If the number of vehicles required for 14 departure times from the old campus to the new campus on a certain day (Monday to Friday) is 7, 6, 4, 3, 1, 1, 4, 3, 1, 2, 1, 2, 1 and 1; The number of vehicles required from the new campus to the old campus is 2, 3, 2, 6, 2, 1, 7, 6, 4, 2, 1 and 1. Through calculation, explore whether the vehicle can realize no-load. If it can be realized, the vehicle arrangement method shall be given; If there must be no load, how can we arrange to minimize the number of empty return vehicles? What if the number of vehicles required from the old campus to the new campus is 9, 8, 4, 3, 1, 1, 4, 3, 1, 2, 1, 2, 1 and 1, and the number of vehicles required from the new campus to the old campus is 3, 4, 2, 6, 2, 1, 7, 8, 4, 2, 1 and 1? Please give the initial number of vehicles in the two campuses, the number of vehicles in the two campuses after stopping operation on the same day, and the total number of empty return vehicles.
Lingo Code:
When switching between one and two small questions, you only need to modify the annotation of target.
MODEL:
!Define set;
SETS:
new/1..12/:new_school,new_time,target_new;
old/1..14/:old_school,old_time,target_old;
un/1..11/;
uo/1..13/;
initial/1/:old_init_num;
ENDSETS
DATA:
new_time=9,10.5,11,12.5,14,15,16,17,18,19,21,22.5;
old_time=7,8,9.3333,10,11,12,12.8333,14,14.8333,16,17,17.8333,21,22.5;
target_new=3,4,2,6, 2,1,7,8, 4,2,1,1;
target_old=9,8,4,3,1,1,4,3,1,2,1,2,1,1;
!target_new=2,3,2,6, 2,1,7,6, 4,2,1,1;
!target_old=7,6,4,3,1,1,4,3,1,2,1,2,1,1;
@ole('C://Users//86183//Desktop//output1_1.xlsx','A')=new_school;
@ole('C://Users//86183//Desktop//output1_1.xlsx','B')=old_school;
@ole('C://Users//86183//Desktop//output1_1.xlsx','S')=old_init_num;
ENDDATA
min=@sum(new(i):(new_school(i)-target_new(i)))+@sum(old(i):(old_school(i)-target_old(i)));
@for(initial(i):
old_init_num(i)>=old_school(1)+old_school(2);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(new(i):
new_school(i)>=target_new(i)
);
@for(old(i):
old_school(i)>=target_old(i)
);
@for(new(i):
@for(uo(j)|(old_time(j)+1)#le#new_time(i) #and# new_time(i)#lt#(old_time(j+1)+1):
(20-old_init_num(1))+(@sum(old(k)|k#le#j:old_school(k))-@sum(new(k)|k#lt#i:new_school(k)))>=new_school(i)
)
);
@for(old(i)|i#ge#3:
@for(un(j)|(new_time(j)+1)#le#old_time(i) #and# old_time(i)#lt#(new_time(j+1)+1):
old_init_num(1)+(@sum(new(k)|k#le#j:new_school(k))-@sum(old(k)|k#lt#i:old_school(k)))>=old_school(i)
)
);
@for(new(i):
@gin(new_school(i))
);
@for(old(i):
@gin(old_school(i))
);
The final solution is:
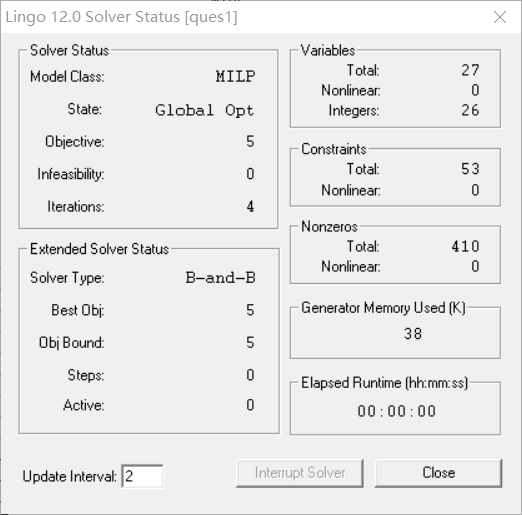
For the second question of question 1, the minimum number of empty returns is 5.
Question 2
If it keeps running continuously every day, the number of vehicles required for each shift in the old campus is still 9,8,4,3,1,1,4,3,1,2,1,2,1,1; The number of vehicles required for each shift in the new campus is still 3,4,2,6,2,1,7,8,4,2,1,1. How can we arrange to minimize the total number of empty return vehicles in a week (Monday to Friday)?
It is required to give the initial number of vehicles in the two campuses on Monday, the number of vehicles in the two campuses after stopping operation on Friday, and the total number of empty return vehicles.
Lingo Code:
MODEL:
!Define set;
SETS:
new/1..12/:new_time,target_new;
old/1..14/:old_time,target_old;
un/1..11/;
uo/1..13/;
initial/1..5/:old_init_num;
days/1..5/;
dayso/1..4/;
newweek(days,new):new_school;
oldweek(days,old):old_school;
ENDSETS
DATA:
new_time=9,10.5,11,12.5,14,15,16,17,18,19,21,22.5;
old_time=7,8,9.3333,10,11,12,12.8333,14,14.8333,16,17,17.8333,21,22.5;
target_new=3,4,2,6, 2,1,7,8, 4,2,1,1;
target_old=9,8,4,3,1,1,4,3,1,2,1,2,1,1;
@ole('C:\Users\86183\Desktop\output2.xlsx','q')=new_school;
@ole('C:\Users\86183\Desktop\output2.xlsx','w')=old_school;
@ole('C:\Users\86183\Desktop\output2.xlsx','e')=old_init_num;
ENDDATA
min=@sum(newweek(i,j):(new_school(i,j)-target_new(j)))+@sum(oldweek(i,j):(old_school(i,j)-target_old(j)));
@for(initial(i):
old_init_num(i)>=old_school(i,1)+old_school(i,2);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(newweek(i,j):
new_school(i,j)>=target_new(j)
);
@for(oldweek(i,j):
old_school(i,j)>=target_old(j)
);
!For the new campus;
@for(days(i):
@for(new(j):
@for(uo(n)|(old_time(n)+1)#le#new_time(j) #and# new_time(j)#lt#(old_time(n+1)+1):
(20-old_init_num(i))+@sum(old(k)|k#le#n:old_school(i,k))-@sum(new(k)|k#lt#j:new_school(i,k))>=new_school(i,j)
)
)
);
!For the old campus;
@for(days(i):
@for(old(j)|j#ge#3:
@for(un(n)|(new_time(n)+1)#le#old_time(j) #and# old_time(j)#lt#(new_time(n+1)+1):
old_init_num(i)+@sum(new(s)|s#le#n:new_school(i,s))-@sum(old(s)|s#lt#j:old_school(i,s))>=old_school(i,j)
)
)
);
@for(dayso(i):old_init_num(i+1)=old_init_num(i)
-@sum(old(j):old_school(i,j))
+@sum(new(j):new_school(i,j))
);
@for(newweek(i,j):
@gin(new_school(i,j))
);
@for(oldweek(i,j):
@gin(old_school(i,j))
);
The final solution is:
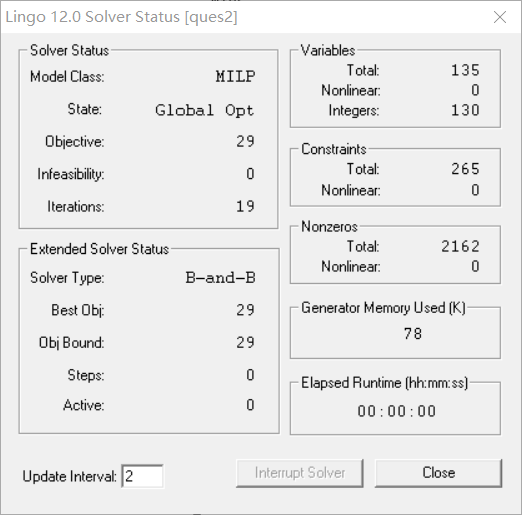
For question 2, the minimum number of empty returns is 29.
Question 3
If the number of vehicles required for each shift in the old campus on Saturday is: 5,4,6,4,3,2; The new campus is: 3,5,7,6,2,1. The number of vehicles required for each shift in the old campus on Sunday is: 5,4,4,6,3,7; The new campus is: 2,6,5,3,3,1. Considering that there are 7 days from Monday to Sunday, how to arrange to minimize the number of empty return vehicles?
It is required to give the initial number of vehicles in the two campuses on Monday, the number of vehicles in the two campuses after stopping operation on Sunday, and the total number of empty return vehicles.
Lingo Code:
MODEL:
!Define set;
SETS:
new/1..12/:new_time,target_new;
old/1..14/:old_time,target_old;
sat_new/1..6/:new_sat_time,target_new_sat,new_school_sat;
sat_old/1..6/:old_sat_time,target_old_sat,old_school_sat;
sun_new/1..6/:new_sun_time,target_new_sun,new_school_sun;
sun_old/1..6/:old_sun_time,target_old_sun,old_school_sun;
un/1..11/;
uo/1..13/;
un_weekend/1..5/;
uo_weekend/1..5/;
initial/1..7/:old_init_num;
days/1..5/;
dayso/1..4/;
sat/1/;
sun/1/;
newweek(days,new):new_school;
oldweek(days,old):old_school;
ENDSETS
DATA:
new_time=9,10.5,11,12.5,14,15,16,17,18,19,21,22.5;
old_time=7,8,9.3333,10,11,12,12.8333,14,14.8333,16,17,17.8333,21,22.5;
new_sat_time=9,11,12.5,17,18,21;
old_sat_time=8,9.3333,12.8333,14,18,20;
new_sun_time=9,11,12.5,17,18,21;
old_sun_time=8,9.3333,12.8333,14,18,20;
target_new=3,4,2,6, 2,1,7,8, 4,2,1,1;
target_old=9,8,4,3,1,1,4,3,1,2,1,2,1,1;
target_new_sat=3,5,7,6,2,1;
target_old_sat=5,4,6,4,3,2;
target_new_sun=2,6,5,3,3,1;
target_old_sun=5,4,4,6,3,7;
@ole('C:\Users\86183\Desktop\output3.xlsx','q')=new_school;
@ole('C:\Users\86183\Desktop\output3.xlsx','w')=old_school;
@ole('C:\Users\86183\Desktop\output3.xlsx','e')=old_init_num;
@ole('C:\Users\86183\Desktop\output3.xlsx','a')=new_school_sat;
@ole('C:\Users\86183\Desktop\output3.xlsx','s')=old_school_sat;
@ole('C:\Users\86183\Desktop\output3.xlsx','d')=new_school_sun;
@ole('C:\Users\86183\Desktop\output3.xlsx','f')=old_school_sun;
ENDDATA
min=@sum(newweek(i,j):(new_school(i,j)-target_new(j)))+@sum(oldweek(i,j):(old_school(i,j)-target_old(j))) +
@sum(sat_new(i):(new_school_sat(i)-target_new_sat(i))) + @sum(sat_old(i):(old_school_sat(i)-target_old_sat(i)))+
@sum(sun_new(i):(new_school_sun(i)-target_new_sun(i))) + @sum(sun_old(i):(old_school_sun(i)-target_old_sun(i)))
;
@for(initial(i)|i#le#5:
old_init_num(i)>=old_school(i,1)+old_school(i,2);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(initial(i)|i#eq#6:
old_init_num(i)>=old_school_sat(1);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(initial(i)|i#eq#7:
old_init_num(i)>=old_school_sun(1);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(newweek(i,j):
new_school(i,j)>=target_new(j)
);
@for(oldweek(i,j):
old_school(i,j)>=target_old(j)
);
@for(sat_new(i):
new_school_sat(i)>=target_new_sat(i)
);
@for(sat_old(i) :
old_school_sat(i)>=target_old_sat(i)
);
@for(sun_new(i):
new_school_sun(i)>=target_new_sun(i)
);
@for(sun_old(i) :
old_school_sun(i)>=target_old_sun(i)
);
!For the new campus;
@for(days(i):
@for(new(j):
@for(uo(n)|(old_time(n)+1)#le#new_time(j) #and# new_time(j)#lt#(old_time(n+1)+1):
(20-old_init_num(i))+@sum(old(k)|k#le#n:old_school(i,k))-@sum(new(k)|k#lt#j:new_school(i,k))>=new_school(i,j)
)
)
);
@for(sat_new(i):
@for(uo_weekend(j)|(old_sat_time(j)+1)#le#new_sat_time(i) #and# new_sat_time(i) #lt#(old_sat_time(j+1)+1):
(20-old_init_num(6))+@sum(sat_old(k)|k#le#j:old_school_sat(k))-@sum(sat_new(k)|k #lt#i:new_school_sat(k))>=new_school_sat(i)
)
);
@for(sun_new(i):
@for(uo_weekend(j)|(old_sun_time(j)+1)#le#new_sun_time(i) #and# new_sun_time(i) #lt#(old_sun_time(j+1)+1):
(20-old_init_num(7))+@sum(sun_old(k)|k#le#j:old_school_sun(k))-@sum(sun_new(k)|k #lt#i:new_school_sun(k))>=new_school_sun(i)
)
);
!For the old campus;
@for(days(i):
@for(old(j)|j#ge#3:
@for(un(n)|(new_time(n)+1)#le#old_time(j) #and# old_time(j)#lt#(new_time(n+1)+1):
old_init_num(i)+@sum(new(s)|s#le#n:new_school(i,s))-@sum(old(s)|s#lt#j:old_school(i,s))>=old_school(i,j)
)
)
);
@for(sat_old(i)|i#ge#2:
@for(un_weekend(j)|(new_sat_time(j)+1)#le#old_sat_time(i) #and# old_sat_time(i)#lt#(new_sat_time(j+1)+1):
old_init_num(6)+(@sum(sat_new(k)|k#le#j:new_school_sat(k))-@sum(sat_old(k)|k#lt#i:old_school_sat(k)))>=old_school_sat(i)
)
);
@for(sun_old(i)|i#ge#2:
@for(un_weekend(j)|(new_sun_time(j)+1)#le#old_sun_time(i) #and# old_sun_time(i)#lt#(new_sun_time(j+1)+1):
old_init_num(7)+(@sum(sun_new(k)|k#le#j:new_school_sun(k))-@sum(sun_old(k)|k#lt#i:old_school_sun(k)))>=old_school_sun(i)
)
);
@for(dayso(i):old_init_num(i+1)=old_init_num(i)
-@sum(old(j):old_school(i,j))
+@sum(new(j):new_school(i,j))
);
@for(sat(i):old_init_num(i+5)=old_init_num(5)
-@sum(old(j):old_school(5,j))
+@sum(new(j):new_school(5,j))
);
@for(sun(i):old_init_num(i+6)=old_init_num(6)
-@sum(sat_old(j):old_school_sat(j))
+@sum(sat_new(j):new_school_sat(j))
);
@for(newweek(i,j):
@gin(new_school(i,j))
);
@for(oldweek(i,j):
@gin(old_school(i,j))
);
@for(sat_new(i):
@gin(new_school_sat(i));
);
@for(sat_old(i):
@gin(old_school_sat(i));
);
@for(sun_new(i):
@gin(new_school_sun(i));
);
@for(sun_old(i):
@gin(old_school_sun(i));
);
The final solution is:
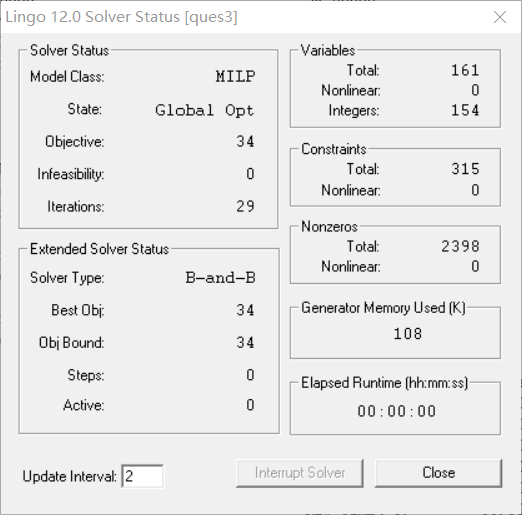
For question 3, the minimum number of empty returns is 34.
Question 4
In the actual vehicle scheduling, it is hoped that it can run continuously every week. Under the requirements of question 3, if the number of vehicles in the two campuses after stopping operation on Sunday is the same as that in the initial two campuses on Monday, how to arrange to minimize the number of empty return vehicles?
It is required to give the number of vehicles in the initial two campuses on Monday or after stopping operation on Sunday, and the total number of empty return vehicles.
Lingo Code:
MODEL:
!Define set;
SETS:
new/1..12/:new_time,target_new;
old/1..14/:old_time,target_old;
sat_new/1..6/:new_sat_time,target_new_sat,new_school_sat;
sat_old/1..6/:old_sat_time,target_old_sat,old_school_sat;
sun_new/1..6/:new_sun_time,target_new_sun,new_school_sun;
sun_old/1..6/:old_sun_time,target_old_sun,old_school_sun;
un/1..11/;
uo/1..13/;
un_weekend/1..5/;
uo_weekend/1..5/;
initial/1..8/:old_init_num;
days/1..5/;
dayso/1..4/;
sat/1/;
sun/1/;
mon/1/;
newweek(days,new):new_school;
oldweek(days,old):old_school;
ENDSETS
DATA:
new_time=9,10.5,11,12.5,14,15,16,17,18,19,21,22.5;
old_time=7,8,9.3333,10,11,12,12.8333,14,14.8333,16,17,17.8333,21,22.5;
new_sat_time=9,11,12.5,17,18,21;
old_sat_time=8,9.3333,12.8333,14,18,20;
new_sun_time=9,11,12.5,17,18,21;
old_sun_time=8,9.3333,12.8333,14,18,20;
target_new=3,4,2,6, 2,1,7,8, 4,2,1,1;
target_old=9,8,4,3,1,1,4,3,1,2,1,2,1,1;
target_new_sat=3,5,7,6,2,1;
target_old_sat=5,4,6,4,3,2;
target_new_sun=2,6,5,3,3,1;
target_old_sun=5,4,4,6,3,7;
@ole('C:\Users\86183\Desktop\output4.xlsx','q')=new_school;
@ole('C:\Users\86183\Desktop\output4.xlsx','w')=old_school;
@ole('C:\Users\86183\Desktop\output4.xlsx','e')=old_init_num;
@ole('C:\Users\86183\Desktop\output4.xlsx','a')=new_school_sat;
@ole('C:\Users\86183\Desktop\output4.xlsx','s')=old_school_sat;
@ole('C:\Users\86183\Desktop\output4.xlsx','d')=new_school_sun;
@ole('C:\Users\86183\Desktop\output4.xlsx','f')=old_school_sun;
ENDDATA
min=@sum(newweek(i,j):(new_school(i,j)-target_new(j)))+@sum(oldweek(i,j):(old_school(i,j)-target_old(j))) +
@sum(sat_new(i):(new_school_sat(i)-target_new_sat(i))) + @sum(sat_old(i):(old_school_sat(i)-target_old_sat(i)))+
@sum(sun_new(i):(new_school_sun(i)-target_new_sun(i))) + @sum(sun_old(i):(old_school_sun(i)-target_old_sun(i)))
;
@for(initial(i)|i#le#5:
old_init_num(i)>=old_school(i,1)+old_school(i,2);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(initial(i)|i#eq#6:
old_init_num(i)>=old_school_sat(1);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(initial(i)|i#eq#7:
old_init_num(i)>=old_school_sun(1);
old_init_num(i)>=0;
old_init_num(i)<=20;
);
@for(newweek(i,j):
new_school(i,j)>=target_new(j)
);
@for(oldweek(i,j):
old_school(i,j)>=target_old(j)
);
@for(sat_new(i):
new_school_sat(i)>=target_new_sat(i)
);
@for(sat_old(i) :
old_school_sat(i)>=target_old_sat(i)
);
@for(sun_new(i):
new_school_sun(i)>=target_new_sun(i)
);
@for(sun_old(i) :
old_school_sun(i)>=target_old_sun(i)
);
!For the new campus;
@for(days(i):
@for(new(j):
@for(uo(n)|(old_time(n)+1)#le#new_time(j) #and# new_time(j)#lt#(old_time(n+1)+1):
(20-old_init_num(i))+@sum(old(k)|k#le#n:old_school(i,k))-@sum(new(k)|k#lt#j:new_school(i,k))>=new_school(i,j)
)
)
);
@for(sat_new(i):
@for(uo_weekend(j)|(old_sat_time(j)+1)#le#new_sat_time(i) #and# new_sat_time(i) #lt#(old_sat_time(j+1)+1):
(20-old_init_num(6))+@sum(sat_old(k)|k#le#j:old_school_sat(k))-@sum(sat_new(k)|k #lt#i:new_school_sat(k))>=new_school_sat(i)
)
);
@for(sun_new(i):
@for(uo_weekend(j)|(old_sun_time(j)+1)#le#new_sun_time(i) #and# new_sun_time(i) #lt#(old_sun_time(j+1)+1):
(20-old_init_num(7))+@sum(sun_old(k)|k#le#j:old_school_sun(k))-@sum(sun_new(k)|k #lt#i:new_school_sun(k))>=new_school_sun(i)
)
);
!For the old campus;
@for(days(i):
@for(old(j)|j#ge#3:
@for(un(n)|(new_time(n)+1)#le#old_time(j) #and# old_time(j)#lt#(new_time(n+1)+1):
old_init_num(i)+@sum(new(s)|s#le#n:new_school(i,s))-@sum(old(s)|s#lt#j:old_school(i,s))>=old_school(i,j)
)
)
);
@for(sat_old(i)|i#ge#2:
@for(un_weekend(j)|(new_sat_time(j)+1)#le#old_sat_time(i) #and# old_sat_time(i)#lt#(new_sat_time(j+1)+1):
old_init_num(6)+(@sum(sat_new(k)|k#le#j:new_school_sat(k))-@sum(sat_old(k)|k#lt#i:old_school_sat(k)))>=old_school_sat(i)
)
);
@for(sun_old(i)|i#ge#2:
@for(un_weekend(j)|(new_sun_time(j)+1)#le#old_sun_time(i) #and# old_sun_time(i)#lt#(new_sun_time(j+1)+1):
old_init_num(7)+(@sum(sun_new(k)|k#le#j:new_school_sun(k))-@sum(sun_old(k)|k#lt#i:old_school_sun(k)))>=old_school_sun(i)
)
);
@for(dayso(i):old_init_num(i+1)=old_init_num(i)
-@sum(old(j):old_school(i,j))
+@sum(new(j):new_school(i,j))
);
@for(sat(i):old_init_num(i+5)=old_init_num(5)
-@sum(old(j):old_school(5,j))
+@sum(new(j):new_school(5,j))
);
@for(sun(i):old_init_num(i+6)=old_init_num(6)
-@sum(sat_old(j):old_school_sat(j))
+@sum(sat_new(j):new_school_sat(j))
);
@for(mon(i):old_init_num(i+7)=old_init_num(7)
-@sum(sun_old(j):old_school_sun(j))
+@sum(sun_new(j):new_school_sun(j))
);
@for(mon(i):old_init_num(i+7)=old_init_num(1)
);
@for(newweek(i,j):
@gin(new_school(i,j))
);
@for(oldweek(i,j):
@gin(old_school(i,j))
);
@for(sat_new(i):
@gin(new_school_sat(i));
);
@for(sat_old(i):
@gin(old_school_sat(i));
);
@for(sun_new(i):
@gin(new_school_sun(i));
);
@for(sun_old(i):
@gin(old_school_sun(i));
);
The final solution is:
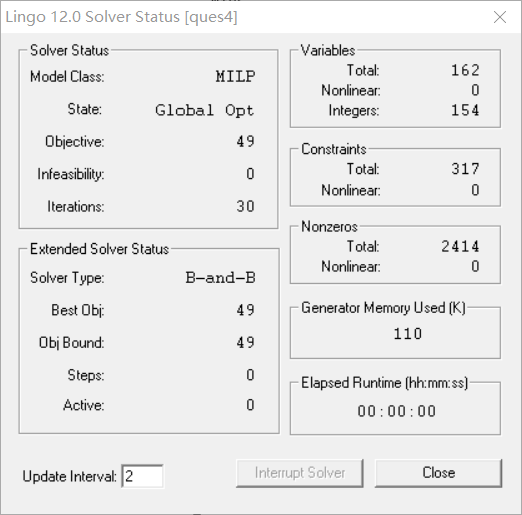
For question 3, the minimum number of empty returns is 49.