And look up the set and map
Joint search set
- There are several types of samples a, b, C and d, assuming V
2) In the parallel search set, each sample is considered to be in a separate set at the beginning
3) The user can call the following two methods at any time:
Boolean issameset (VX, V, y): query whether sample x and sample y belong to a set
Void Union (V, x, V, y): merge all samples of the respective sets of X and Y into -- sets - The lower the cost of the isSameSet and union methods, the better
Steps:
Establish a map, where k is the node and v is the pointing node of the node
1. The first step is to integrate all their numbers into a set (each node forms a set separately)
2. In a set, each node is the representative node in its own set. When the set is merged, if it is decided to hang 2 under 1, only 1 node in the set where 2 is located points to itself, so 1 is the representative node of the set.
3. Since each set has a representative node of a set, you can judge whether it is in the same set through the representative node, or you can connect the representative node of another set to this set. At this time, the whole set has only one representative node to realize the integration of the set. (first, judge the number of elements and hang the set of few elements under the multi elements)
Optimization: in the process of upward lookup, all elements on the path are directly connected to the representative node.
import java.util.HashMap;
import java.util.List;
import java.util.Stack;
public class Code04_UnionFind {
public static class Element<V> {//Add a package
public V value;
public Element(V value) {
this.value = value;
}
}
public static class UnionFindSet<V> {
public HashMap<V, Element<V>> elementMap;//v is the value [user courseware], and Element is the Element [for your own use]
public HashMap<Element<V>, Element<V>> fatherMap;//Parent node
public HashMap<Element<V>, Integer> sizeMap;//How many nodes are there in the collection representing nodes
public UnionFindSet(List<V> list) {
elementMap = new HashMap<>();
fatherMap = new HashMap<>();
sizeMap = new HashMap<>();
for (V value : list) {
//initialization
Element<V> element = new Element<V>(value);
elementMap.put(value, element);
fatherMap.put(element, element);//Each node is its own parent
sizeMap.put(element, 1);//Each node is its own representative node
}
}
private Element<V> findHead(Element<V> element) {
Stack<Element<V>> path = new Stack<>();//The road along the way
while (element != fatherMap.get(element)) {
path.push(element);//Go all the way to the representative node
element = fatherMap.get(element);
}
while (!path.isEmpty()) {
//Flattening, all nodes directly point to the representative nodes
fatherMap.put(path.pop(), element);
}
return element;
}
public boolean isSameSet(V a, V b) {
//See if a has registered. Each value has a corresponding element
if (elementMap.containsKey(a) && elementMap.containsKey(b)) {
return findHead(elementMap.get(a)) == findHead(elementMap.get(b));
}
// If a point has not been registered, it will not be searched
return false;
}
public void union(V a, V b) {
if (elementMap.containsKey(a) && elementMap.containsKey(b)) {
//Find the representative node [header node] first
Element<V> aF = findHead(elementMap.get(a));//Find the representative node of the element corresponding to a
Element<V> bF = findHead(elementMap.get(b));//Represents the size of this combination in the node
if (aF != bF) {
int aSetsize = sizeMap. get(aHead);
int bSetSize = sizeMap . get(bHead);
// If bf is small, hang the small node on the large node and directly record in the subtropical high parents
if (aSetSize >= bSetSize) {
parents . put(bF, aF);
sizeMap. put(aF, aSetSize + bSetSize); .
sizeMap . remove(bF);
} else {
parents . put( aF, bF);
sizeMap . put(bHead, aSetSize + bSetSize);
sizeMap . remove(bF);
}
}
}
}
}
Island issue
There are only two values of 0 and 1 in a matrix. Each position can match its own up, down, left and right
- Four positions are connected. If a piece of 1 is connected together, this part is called an island. How many islands are there in a matrix?
- give an example:
0 0 1 0 1 0
1 1 1 0 1 0
1 0 0 1 0 0
0 0 0 0 0 0
There are three islands in this matrix.
public static int countIslands(Int[][] m){
if(m == null || m[0] == null){
return 0;
}
int N = m.length;
int M = m[0].length;
int res = 0;
for(int i = 0;i<N;i++){
for(int j = 0;j<M;j++{
if(m[i][j] == 1){
res++;
infect(m,i,j,N,M);
}
}
}
return res;
}
public static void infect(int[][]m,int i,int j,int N,int M){
if(i<0 || i>=N||j<0||j>=M || m[i][j] != 1){
return ;
}
m[i][j] =2;
infect(m,i+1,j,N,M);
infect(m,i,j+1,N,M);
infect(m,i-1,j,N,M);
infect(m,i,j-1,N,M);
}
Sharding matrix, parallel
Core logic: cutting matrix. Divide into n blocks and record the boundary information
Let's Mark 2 near the knife as belonging to A. then when merging, let's see if ac is a set, no, but the knife is left and right, so it is merged into an island.
/pic:mw://ab700fc9385dd3b9f86fbd2cc0c71d65
Record the boundary information, establish nodes, and then use the union set to judge how many sets there are
chart
1) It consists of a set of points and a set of edges
2) Although there are the concepts of directed graph and undirected graph, they can be expressed by directed graph
3) There may be weights on the edges

Figure:
public class Graph {
public HashMap<Integer,Node> nodes;//Collection of points
public HashSet<Edge> edges;//Set of edges
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
Point:
public class Node {
public int value;//Value of node
public int in;//Penetration (how many nodes point to me)
public int out;//Out degree (how many nodes do I point to)
public ArrayList<Node> nexts;//The next level node that can be reached from me, the neighbor node
public ArrayList<Edge> edges;//A collection of edges emanating from me
public Node(int value) {
this.value = value;
in = 0;
out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}
Edge:
public class Edge {
public int weight;//What is the weight of this edge
public Node from;//Where does this side start
public Node to;//Where did this side arrive
public Edge(int weight, Node from, Node to) {
this.weight = weight;
this.from = from;
this.to = to;
}
}
Graph generator:
public class GraphGenerator {
public static Graph createGraph(Integer[][] matrix) {//Enter a matrix
Graph graph = new Graph();//Initialize custom graph
for (int i = 0; i < matrix.length; i++) {
Integer weight = matrix[i][0];//Edge weights
Integer from = matrix[i][1];//Sequence of from nodes
Integer to = matrix[i][2];//Sequence of to nodes
if (!graph.nodes.containsKey(from)) {//First check whether the from node exists. If it does not exist, create it
graph.nodes.put(from, new Node(from));
}
if (!graph.nodes.containsKey(to)) {//Then check whether the to node exists. If it does not exist, it will be established
graph.nodes.put(to, new Node(to));
}
Node fromNode = graph.nodes.get(from);//Take out the from point
Node toNode = graph.nodes.get(to);//Take out some
Edge newEdge = new Edge(weight, fromNode, toNode);//Create a new edge
fromNode.nexts.add(toNode);//The adjacency point of from adds a to node
fromNode.out++;//from plus 1
toNode.in++;//to node penetration plus 1
fromNode.edges.add(newEdge);//The edge set of the from node increases
graph.edges.add(newEdge);//Add to the edge set of the whole graph
}
return graph;
}
}
Breadth first traversal
1. Using queue
2. Start from the source node, enter the queue according to the width, and then pop up
3. For each pop-up point, put all adjacent points of the node that have not entered the queue into the queue
4. Wait until the queue becomes empty
public class Code_01_BFS {
public static void bfs(Node node) {//Breadth first traversal
if (node == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
HashSet<Node> map = new HashSet<>();
queue.add(node);
map.add(node);
while (!queue.isEmpty()) {
Node cur = queue.poll();//Take out the current node
System.out.println(cur.value);//Print current node
for (Node next : cur.nexts) {//Traverse all adjacent points of the current node
if (!map.contains(next)) {//If an adjacent node is already in the set, it is no longer needed
map.add(next);
queue.add(next);
}
}
}
}
}
Depth first traversal
1. Using stack
2. Start from the source node, put the node into the stack according to the depth, and then pop up
3. For each pop-up point, put the next adjacent point of the node that has not been in the stack into the stack
4. Until the stack becomes empty
public class Code_02_DFS {
public void dfs(Node node){
if(node == null){
return;
}
Stack<Node> stack = new Stack<>();
HashSet<Node> set = new HashSet<>();
stack.add(node);
set.add(node);
System.out.println(node.value);
while (!stack.isEmpty()){
Node cur = stack.pop();
for(Node next : cur.nexts){
if(!set.contains(next)){//If there is no next node in the set, continue
stack.push(cur);//First put the current node back on the stack
stack.push(next);//Then put the next node into the stack
set.add(next);//Add the next node to the set
System.out.println(next.value);//Prints the value of the next node
break;//No longer continue the current loop, return to the while loop and continue the traversal of the next node
}
}
}
}
}
Topological sorting algorithm
Scope of application: it is required to have a directed graph, nodes with penetration of 0, and no ring
The logic of the implementation is: first find the nodes with a penetration of 0, then print them, and delete them immediately after printing, then continue to search the graph, find new nodes with a penetration of 0, and continue the previous operation until the graph is completely traversed.
public class Code_03_TopologySort {
// directed graph and no loop
public static List<Node> sortedTopology(Graph graph) {
HashMap<Node, Integer> inMap = new HashMap<>();//Record all entry points
Queue<Node> zeroInQueue = new LinkedList<>();//Record all nodes with a penetration of 0
for (Node node : graph.nodes.values()) {//values means all the current points
inMap.put(node, node.in);//Register all entry points
if (node.in == 0) {
zeroInQueue.add(node);//Register all nodes with a penetration of 0
}
}
List<Node> result = new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
Node cur = zeroInQueue.poll();
result.add(cur);
for (Node next : cur.nexts) {
inMap.put(next, inMap.get(next) - 1);//Find a new point with a penetration of 0
if (inMap.get(next) == 0) {
zeroInQueue.add(next);
}
}
}
return result;
}
}
Minimum spanning tree and related algorithms
Several conceptual definitions of graphs:
Connected graph: in an undirected graph, if any two vertices vivi and vjvj have paths connected, the undirected graph is called a connected graph.
Strongly connected graph: in a directed graph, if any two vertices vivi and vjvj have paths connected, the directed graph is called strongly connected graph.
Connected network: in a connected graph, if the edges of the graph have a certain meaning, each edge corresponds to a number, which is called weight; Weight represents the cost of connecting vertices. This connected graph is called a connected network.
Spanning tree: the spanning tree of a connected graph refers to a connected subgraph, which contains all n vertices in the graph, but only enough n-1 edges to form a tree. A spanning tree with n vertices has only n-1 edges. If another edge is added to the spanning tree, it must be a ring.
Minimum spanning tree: in all spanning trees of a connected network, the cost of all edges and the minimum spanning tree are called minimum spanning trees.
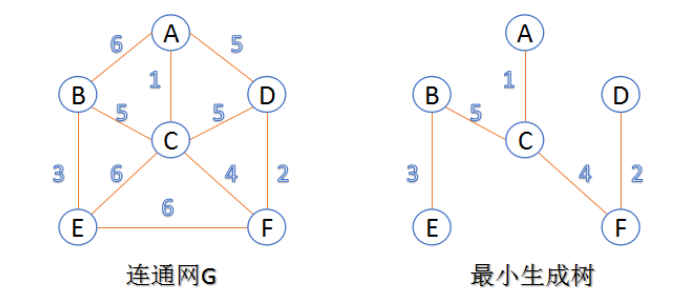
Application scope of kruskal algorithm (K algorithm): undirected graph is required
1) Always start from the edge with the smallest weight and investigate the edge with the larger weight in turn
2) The current edge either enters the collection of the minimum spanning tree or is discarded
3) If the current edge enters the set of the minimum spanning tree and does not form a ring, the current edge is selected
4) If the current edge enters the set of the minimum spanning tree to form a ring, do not use the current edge
5) After examining all the edges, the set of the minimum spanning tree is also obtained
This algorithm can be called "edge adding method". The initial minimum number of spanning tree edges is 0. Each iteration selects a minimum cost edge that meets the conditions and adds it to the edge set of the minimum spanning tree.
All edges in the graph are sorted according to the cost from small to large;
The n vertices in the graph are regarded as a forest composed of independent n trees;
Select the edge from small to large according to the weight. If the two vertices UI, viui and VI connected by the selected edge belong to two different trees, they will become one edge of the minimum spanning tree, and the two trees will be merged as one tree.
Repeat (3) until all vertices are in a tree or have n-1 edges.

//undirected graph only
public class Code_04_Kruskal {
// Union-Find Set
public static class UnionFind {
private HashMap<Node, Node> fatherMap;
private HashMap<Node, Integer> rankMap;
public UnionFind() {
fatherMap = new HashMap<Node, Node>();
rankMap = new HashMap<Node, Integer>();
}
private Node findFather(Node n) {
Node father = fatherMap.get(n);
if (father != n) {
father = findFather(father);
}
fatherMap.put(n, father);
return father;
}
public void makeSets(Collection<Node> nodes) {
fatherMap.clear();
rankMap.clear();
for (Node node : nodes) {
fatherMap.put(node, node);
rankMap.put(node, 1);
}
}
public boolean isSameSet(Node a, Node b) {
return findFather(a) == findFather(b);
}
public void union(Node a, Node b) {
if (a == null || b == null) {
return;
}
Node aFather = findFather(a);
Node bFather = findFather(b);
if (aFather != bFather) {
int aFrank = rankMap.get(aFather);
int bFrank = rankMap.get(bFather);
if (aFrank <= bFrank) {
fatherMap.put(aFather, bFather);
rankMap.put(bFather, aFrank + bFrank);
} else {
fatherMap.put(bFather, aFather);
rankMap.put(aFather, aFrank + bFrank);
}
}
}
}
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> kruskalMST(Graph graph) {
UnionFind unionFind = new UnionFind();
unionFind.makeSets(graph.nodes.values());
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
for (Edge edge : graph.edges) {
priorityQueue.add(edge);
}
Set<Edge> result = new HashSet<>();
while (!priorityQueue.isEmpty()) {
Edge edge = priorityQueue.poll();
if (!unionFind.isSameSet(edge.from, edge.to)) {
result.add(edge);
unionFind.union(edge.from, edge.to);
}
}
return result;
}
}
Prim algorithm (P algorithm)
This algorithm can be called "point adding method". Each iteration selects the point corresponding to the edge with the lowest cost and adds it to the minimum spanning tree. The algorithm starts from a vertex s and gradually grows to cover all vertices of the whole connected network.
All vertex sets of the graph are VV; Initial order set u={s},v=V − uu={s},v=V − u;
Among the edges that can be composed of two sets u, VU and V, select the least cost edge (u0,v0)(u0,v0), add it to the minimum spanning tree, and incorporate v0v0 into set U.
Repeat the above steps until the minimum spanning tree has n-1 edges or n vertices.
Since points are added to the set u, the minimum cost edge must be updated synchronously; An auxiliary array closedge needs to be established to maintain the information of each vertex in set v and the least cost edge in set U
// undirected graph only
public class Code_05_Prim {
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> primMST(Graph graph) {
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(
new EdgeComparator());
HashSet<Node> set = new HashSet<>();
Set<Edge> result = new HashSet<>();
for (Node node : graph.nodes.values()) {
if (!set.contains(node)) {
set.add(node);
for (Edge edge : node.edges) {
priorityQueue.add(edge);
}
while (!priorityQueue.isEmpty()) {
Edge edge = priorityQueue.poll();//Pop the smallest edge from the priority queue
Node toNode = edge.to;
if (!set.contains(toNode)) {
set.add(toNode);
result.add(edge);
for (Edge nextEdge : toNode.edges) {
priorityQueue.add(nextEdge);
}
}
}
}
}
return result;
}
}
Dijkstra's algorithm
Solve the shortest path problem of unit points: given the weighted directed graph G and source point v, find the shortest path from V to other vertices in G
Limiting condition: there is no edge with negative weight in graph G
The dijestra algorithm has done two things in total:
[1] Continuously run the breadth first algorithm to find the visible point and calculate the distance from the visible point to the source point
[2] Select the shortest length from the currently known paths and add its vertices to S as the vertices that determine the shortest path found.
// no negative weight
public class Code_06_Dijkstra {
public static HashMap<Node, Integer> dijkstra1(Node from) {
HashMap<Node, Integer> distanceMap = new HashMap<>();
distanceMap.put(from, 0);
//Selected nodes
HashSet<Node> selectedNodes = new HashSet<>();
Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
while (minNode != null) {
int distance = distanceMap.get(minNode);
for (Edge edge : minNode.edges) {
Node toNode = edge.to;
if (!distanceMap.containsKey(toNode)) {
distanceMap.put(toNode, distance + edge.weight);
}
distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));
}
selectedNodes.add(minNode);
minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
}
return distanceMap;
}
public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap,
HashSet<Node> touchedNodes) {
Node minNode = null;
int minDistance = Integer.MAX_VALUE;
for (Entry<Node, Integer> entry : distanceMap.entrySet()) {
Node node = entry.getKey();
int distance = entry.getValue();
if (!touchedNodes.contains(node) && distance < minDistance) {
minNode = node;
minDistance = distance;
}
}
return minNode;
}
public static class NodeRecord {
public Node node;
public int distance;
public NodeRecord(Node node, int distance) {
this.node = node;
this.distance = distance;
}
}
public static class NodeHeap {
private Node[] nodes;
private HashMap<Node, Integer> heapIndexMap;
private HashMap<Node, Integer> distanceMap;
private int size;
public NodeHeap(int size) {
nodes = new Node[size];
heapIndexMap = new HashMap<>();
distanceMap = new HashMap<>();
this.size = 0;
}
public boolean isEmpty() {
return size == 0;
}
public void addOrUpdateOrIgnore(Node node, int distance) {
if (inHeap(node)) {
distanceMap.put(node, Math.min(distanceMap.get(node), distance));
insertHeapify(node, heapIndexMap.get(node));
}
if (!isEntered(node)) {
nodes[size] = node;
heapIndexMap.put(node, size);
distanceMap.put(node, distance);
insertHeapify(node, size++);
}
}
public NodeRecord pop() {
NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0]));
swap(0, size - 1);
heapIndexMap.put(nodes[size - 1], -1);
distanceMap.remove(nodes[size - 1]);
nodes[size - 1] = null;
heapify(0, --size);
return nodeRecord;
}
private void insertHeapify(Node node, int index) {
while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) {
swap(index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private void heapify(int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left])
? left + 1 : left;
smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index;
if (smallest == index) {
break;
}
swap(smallest, index);
index = smallest;
left = index * 2 + 1;
}
}
private boolean isEntered(Node node) {
return heapIndexMap.containsKey(node);
}
private boolean inHeap(Node node) {
return isEntered(node) && heapIndexMap.get(node) != -1;
}
private void swap(int index1, int index2) {
heapIndexMap.put(nodes[index1], index2);
heapIndexMap.put(nodes[index2], index1);
Node tmp = nodes[index1];
nodes[index1] = nodes[index2];
nodes[index2] = tmp;
}
}
public static HashMap<Node, Integer> dijkstra2(Node head, int size) {
NodeHeap nodeHeap = new NodeHeap(size);
nodeHeap.addOrUpdateOrIgnore(head, 0);
HashMap<Node, Integer> result = new HashMap<>();
while (!nodeHeap.isEmpty()) {
NodeRecord record = nodeHeap.pop();
Node cur = record.node;
int distance = record.distance;
for (Edge edge : cur.edges) {
nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);
}
result.put(cur, distance);
}
return result;
}
}