catalogue
Analysis of simple matching algorithm:
Preprocessing: find fingerprint
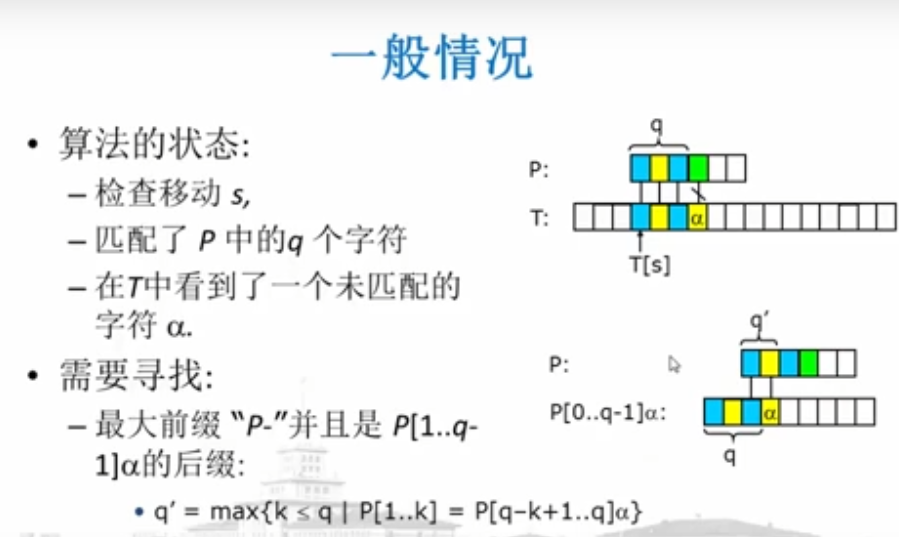
Step: the key is the calculation of each shift
The prefix table of size m is pre calculated to store the value of π [q] (0 < = q
String matching problem:
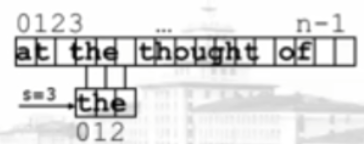
Input:
Text T = "at the thought of"
n=length(T) =17
Mode P="the"
m=length(P) = 3
Output: move to S (S is the subscript in the text)
S is the minimum integer satisfying t [s.. S + M-1] = P [0.. M-1] (0 < = s < = n-m)
If no such s exists, - 1 is returned
Simple matching algorithm:
Violent search: check all values from 0 to n-m
Pseudo code
Native-Search (T,P) for s <- 0 to n-m j <- 0 //check if T[s..s+m-1] = P[0..m-1] while T[s+j]= P[j] do j <- j+1 if j = m return s return -1
How many comparisons are needed to make t = "at the thought of", P = "though"?
Analysis of simple matching algorithm:
Worst case scenario:
- Outer loop: n-m [how many times does the first letter of P align with the letter of T]
- Inner circulation: m []
- Total (n-m)*m = O(nm)
- What inputs produce the worst case? [each time P is matched, the mismatch is found only after the last one]
Best case: n-m [mismatch found at the beginning of each time]
Completely random text and patterns: O(n-m)
Idea: if the text is completely random and the alphabet size is k, then any two letters are 1/k each. Comparing the first letter of P and T, the probability of their matching is 1/k and the probability of mismatch is 1-1/k. The probability of exactly two comparisons is (1/k) * (1-1/k)
7.2 Rabin Karp algorithm
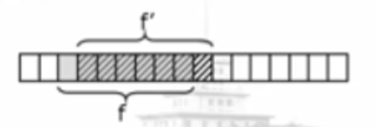
Fingerprint idea
Assumptions:
- We can calculate the fingerprint f(P) of a P in O(m) time
- If the fingerprints are not equal, f(P) ≠ f (T[s..s+m-1]), then the substrings are not equal
- We can compare fingerprints at O(1) time
- We can calculate the current fingerprint of F '(t [S + 1.. S + M]) and the fingerprint after moving one bit from F (t [s.. S + M-1]) at O(1)
Fingerprint based algorithm:
Let the alphabet be Σ = {0,1,2,3,4,5,6,7,8,9}
Make the fingerprint a decimal number, that is, f("1045") =1*10**3 + 0*10**2 +4*10**1 + 5 =1045
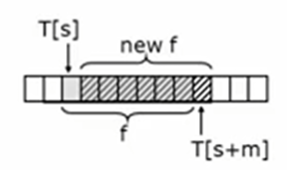
Fingerprint-Search (T,P) fp <- compute f(P) //Pattern or reference substring f <- compute f(T[0..m-1]) for s <- 0 to n-m do if fp = f return s f <- (f - T[s]*10**(m-1) )*10 + T[s+m] return -1
The running time is 2 O (m) + O (n-m) = O (n)
Start counting two fingerprints 2 O(m) + time for sequential comparison n-m rounds, each round is O(1)
Using the Hash function
Problem: in fact, we can't assume that we can perform arithmetic operation on m digits in O(1) time.
Solution: use the hash function h = f mod q
For example, if q = 7, H ("52") = 52 mod 7 = 3
h(S1) ≠ h(S2) => S1 ≠ S2
But h(S1) = h(S2) does not mean S1 = S2
For example, if q = 7, H ("73") = 3 but "73" ≠ "52"
But mod arithmetic operation - the operand is limited to Q. if q is small enough / constant, it can be in O(1)
Arithmetic operation in time
(a+b)mod q= (a mod q +b mod q)mod q
(a*b)mod q=(a mod q)*(b mod q)mod q
Preprocessing: find fingerprint
Disassemble (Qin Jiushao)
fp=P[m-1] + 10* ( P[m-2] + 10*(P[m-3] +...+10*(P[1] + 10* (P[0]) ) ) mod q
ft can also be calculated from T[0...m-1]
For example, P = "2531", q = 7, FP =?
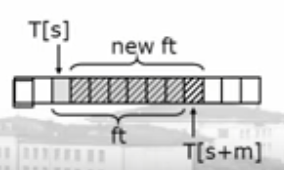
Step: the key is the calculation of each shift
ft = ( ft-T[s]*10**(m-1) mod q) *10 + T[s+m] ) mod q
//T[s+m] is less than Q, and mod q is not required. The formula T[s]*10**(m-1) may be greater than Q, and mod q is required, while T[s] is also less than Q, so mod q is required for 10**(m-1)
10**(m-1) mod q is calculated once in the pretreatment
Rabin Karp algorithm:
Karbin-Karp-Search (T,P) q <- a prime larger than m//Select a prime number q greater than m to c <- 10**(m-1) mod q //run a loop multiplying by 10 mod q fp <- 0 ; ft <- 0 for i <- 0 to m-1 //preprocessing fp <- (10*dp +P[i] ) mod q ft <- (10*ft +T[i] ) mod q for s <- 0 to n-m //Matching matching if fp= ft then //Fingerprint equality does not mean string matching if P[0..m-1] = T[s..s+m-1] return s//You also need to match each character ft <- ( (ft - T[s]*c ) *10 + T[s+m ] ) mod q //displacement return -1
How many times?
analysis:
If q is a prime number, the hash function will make the m-bit string evenly distributed among Q values.
Therefore, only every q times in s rotation needs to match the fingerprint (matching is slow, and O(m) times need to be compared). Every q time you need a fingerprint, others need a comparison.
Expected running time (if Q > m)
Preprocessing: O(m) / / each Pattern character needs to be calculated once
External circulation: O(n-m) / / ratio from head to tail
All internal loops: (n-m)/q * m = O(n-m) / / specific fingerprint comparison
Total time: O(n-m) / / linear
Worst run time: O(nm) / / and violent search are matched every time, but it is found that the last letter is different every time
Application:

KMP algorithm
Matching of N comparisons
Target: each character in the text matches only once
Simple algorithm problem:
The knowledge in the existing partial matching is not utilized
T="Tweedledee and Tweedledum" P="Tweedledum"
T="pappar" P="pappappappar"
Automata search
Algorithm:
Pretreatment:
For each Q (1 < = q < = m-1) and each α ∈∑ calculate a new value of Q in advance and record it as σ (q, α)
Fill in a table with the size of m * ∑
Scan text:
When a mismatch is found, (P[q] ≠ T[s+q]): set s=s+q - σ (q, α)+ 1, and q = σ (q, α)
Analysis:
Match phase O(n)
Disadvantages: too much memory, O (m |∑|), too many preprocessing o (m |∑|)
Prefix function:
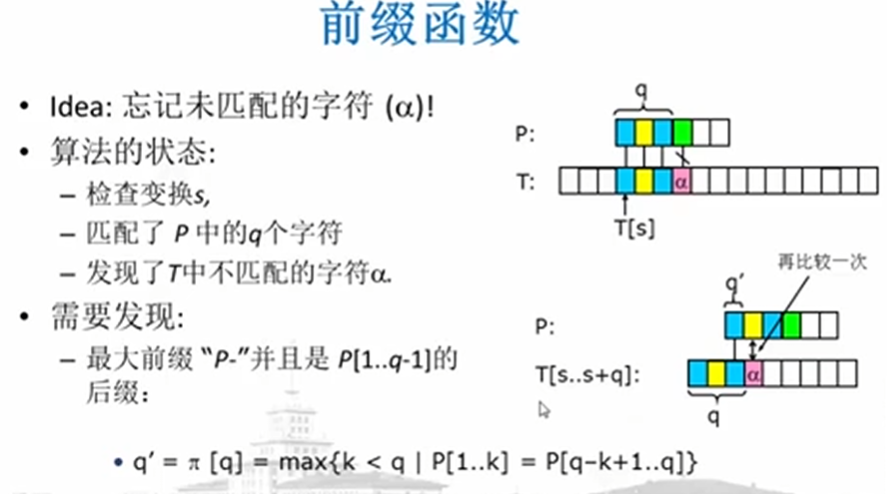
Prefix table:
Pre calculate the prefix table with size m to store the value of π [q] (0 < = q < m, m= length(P))

KMP-Search(T,P)
{
π<- Compute-Prefix-Table(P)
q <- 0 //Number of matching characters
for i <- 0 to n-1 //Scan text from left to right
while q >0 and P[q] ≠T[i] do
q <- π[q]
if P[q] = T[i] then q <- q+1
if q= m then return i-m+1
return -1
}
//Compute prefix table is the essence of executing KMP algorithm on P KMP analysis
Worst case running time: O(n+m)
- Main algorithm: O(n)
- Compute-Prefix-Table : O(m)
Space: O (m)
Main algorithm: match twice at most
BMH algorithm:
Inverse simple algorithm:
Start searching after P.
Boyer and Moore
Reverse-Naive-Search (T,P) for s <- 0 to n-m j <- m-1 //Start at the end //check if T[s..s+m-1] = P[0..m-1] while T[s+j] = P[j] do j <- j-1 if j< 0 return s return -1
The running time is the same as that of the simple algorithm.
Heuristic method:

Match P and T, from back to front,
et a and e find a mismatch. At this time, only look at which of the last letter E and P can match (except the last E has been compared),
No, at this time, you can string P after e, which is equivalent to string "date" to cative,
From the back to the front, e is different from v. match T[s+n-1] with this v into the pattern, remove the last bit, and appear on the right except the one that has been compared. We know that there is no v in front, so we can string the date four digits later,
At this time, align d to the position of e behind v, and then find that E and a don't match,
Then look for a in the prefix of P. if you find an a, align the positions of the two a, and then e t a d will be found.
Offset table:
If the last letter appears in P In the prefix of, calculate P How many positions can you move back to align with him? If it doesn't appear, skip.
In the preprocessing, the offset table with the size of ∑ is calculated.
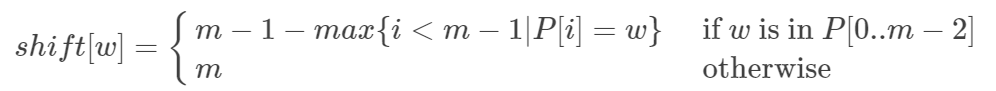
Example: P="kettle" remove the prefix "kettl" from the last letter. If the last letter is "e", shift [e] = 4, shift [l] = 1, shift [t] = 2, shift [k] = 5
Pseudo code:
BMH-Search (T,P)
n <- the length of T
m <- the length of P
|∑| <- the length of OffsetTable
//Calculate the offset table of P
for c <- 0 to |∑| -1
shift[c] =m //Default value
for k <- 0 to m-2
shift[P[k]] = m-1 -k
//search
s <- 0
while s <= n - m do
j <- m-1 //Start at the end
// check if T[s..s+m-1] = P[0..m-1]
while T[s+j] = P[j] do
j <- j-1
if j < 0 return s
s <- s + shift[ T[s+m-1] ] //shift by last letter
return -1 Algorithm implementation:
#include<bits/stdc++.h>
using namespace std;
const int maxnum=1005;
int shift[maxnum];
int BMH(string &T,string &P)
{
int n=T.length();
int m=P.length();
//Offset table
for(int i=0;i<maxnum;i++)
{
shift[i]=m;//Default value
}
//The last subscript of each letter in the pattern string P, (except the last letter)
//The main string never matches the last character and the number of bits to be shifted left
for(int i=0;i<=m-2;i++)
{
shift[P[i]]=m-1-i;//Character numeric
}
int s=0;// Where is the starting position of the mode string in the main string
while(s <= n-m)
{
int j=m-1;// Match from the end of the pattern string
while(T[s+j]==P[j])
{
j=j-1;
if(j<0)return s;// Match successful
}
// Bad character found (the last character that currently matches the pattern string)
// The last position in the pattern string (except the last bit)
// The number of steps required to move from the end of the pattern string to this position
s=s+shift[ T[s+m-1] ];
}
return -1;
}
int main()
{
string T,P;
while(true)
{
getline (cin,T);
getline(cin,P);
//
int res=BMH(T,P);
if(res==-1 )
cout<<"Mismatch"<<endl;
else
cout<<"Pattern string P The position of the main string is:"<<res<<endl;
}
return 0;
} test
at the thought of though Pattern string P The position in the main string is: 7 aaaaaaab aaa Pattern string P The position in the main string is: 0
BMH analysis:
Worst case run time:
- Pretreatment: O(124∑| + m)
- Search: O(nm)---
- Total: O(nm)
Space: O(∑)
- And m independent
Very fast on real data sets.