Experimental environment
Windows 10+DEV-C++
dynamic programming
Dynamic programming is a hot topic in algorithm design and analysis. If the optimal solution of a problem (usually the maximum or minimum value) is required, and the problem can be decomposed into several problems, and there are overlapping subproblems between small problems, dynamic programming is considered.
Features using dynamic programming
Use dynamic planning features:
- Find the optimal solution of a problem
- Large problems can be decomposed into subproblems, and subproblems have smaller overlapping subproblems
- The optimal solution of the whole problem depends on the optimal solution of the subproblem (state transition equation)
- Analyze problems from top to bottom and solve problems from bottom to top
- Discuss the underlying boundary problem
1. Matrix multiplication problem
Problem description
Given n matrices {A1,A2,..., An}, where Ai and Ai+1 are multiplicative, i=1,2,..., n-1. How to determine the calculation order of matrix continued product, so that the number of times required to calculate matrix continued product according to this order is the least. For example:
A1={30x35} ;A2={35x15} ;A3={15x5} ;A4={5x10} ;A5={10x20} ;A6={20x25} ;
The final result is that the minimum multiplication of ((A1(A2A3))((A4A5)A6)) is 15125.
Problem solving ideas
One property of usable dynamic programming is the optimal substructure property, that is, the order of the calculation matrix sub chain A[i:k] and A[k+1:j] contained in the optimal order of A[i:j] is also optimal. The dynamic programming algorithm can solve this problem in a bottom-up manner according to its recursive formula (that is, start from the smallest). During the calculation, save the answers to the solved sub questions. Each subproblem is calculated only once, and only a simple check is needed later, so as to avoid a large number of repeated calculations, and finally get the polynomial time algorithm. We can calculate the result according to the following formula. Where p[i-1] represents the row number of the ith matrix, p[k] represents the last column number of i:k matrix combined, and p[j] is the column number of k+1:j combined. The calculation method of this part is actually to calculate the total number of times when two matrices are multiplied.
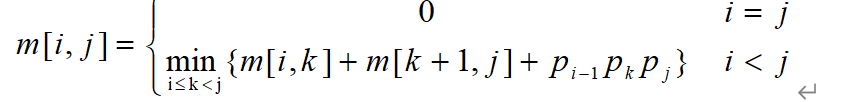
#include<iostream>
using namespace std;
const int N=7;
//p is the matrix chain, p[0],p[1] represents the number of rows and columns of the first matrix, p[1],p[2] represents the number of rows and columns of the second matrix Length is the length of p
//Therefore, if there are six matrices, length=7, m is the two-dimensional matrix for storing the optimal result, and s is the matrix for storing the route for selecting the optimal result
//Two dimensional matrix
void MatrixChainOrder(int *p,int m[N][N],int s[N][N],int length)
{
int n=length-1;
int l,i,j,k,q=0;
//m[i][i] has only one matrix, so the multiplication number is 0, that is, m[i][i]=0;
for(i=1;i<length;i++)
{
m[i][i]=0;
}
//l represents the length of the matrix chain
// When l=2, calculate m [I, I + 1], I = 1,2, N-1 (minimum cost of chain with length l=2)
for(l=2;l<=n;l++)
{
for(i=1;i<=n-l+1;i++)
{
j=i+l-1; //Take i as the starting position and j as the end of the chain with length l,
m[i][j]=0x7fffffff;
//k from i to j-1, divided by k
for(k=i;k<=j-1;k++)
{
q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q;
s[i][j]=k;
}
}
}
}
cout << m[1][N-1] << endl;
}
void PrintAnswer(int s[N][N],int i,int j)
{
if(i==j)
{
cout<<"A"<<i;
}
else
{
cout<<"(";
PrintAnswer(s,i,s[i][j]);
PrintAnswer(s,s[i][j]+1,j);
cout<<")";
}
}
int main()
{
int p[N]={30,35,15,5,10,20,25};
int m[N][N],s[N][N];
MatrixChainOrder(p,m,s,N);
PrintAnswer(s,1,N-1);
return 0;
}

2. Rope cutting
Problem description
Here is a rope with length n. please cut the rope into m segments (M and N are integers). The length of each segment of rope is recorded as k[0],k[1],k[2] How to cut the rope to maximize the product of k[0],k[1],k[2]
For example, the rope length n=8 and the maximum product 18 = 233 are cut into m=3 segments.
Problem solving ideas
The bottom-up dynamic programming method is adopted. Let f(n) represent the maximum product of several sections of the rope cut with length n. if the first knife goes down and the length of the first section is I, then the rest needs to be cut n-i, then f(n)=max{f(i)f(n-i)}. The optimal solution of f(n) corresponds to the optimal solution of f(i) and f(n-i). If f(i) is not the optimal solution, the product of the optimal solution and f(n-i) must be greater than the optimal solution of f(n), which is contradictory to the optimal solution of f(n). Therefore, the optimal solution of f(n) corresponds to the optimal solution of f(i) and f(n-i).
Firstly, cutting the rope is the optimal solution problem. Secondly, large problems contain small problems, and the optimal solution of large problems contains the optimal solution of small problems. Therefore, dynamic programming can be used to solve the problem, and the optimal solution of small problems can be recorded in the array from small to large. When finding the optimal solution of large problems, it can be obtained directly to avoid repeated calculation.
When n < 2, it returns 0 because it is cut at least once each time. When n=2, it can only be cut into two 1s, then 1 is returned. When n=3, it can be cut into three ones, or 1 and 2, then the maximum product is 2. When n > 3, the formula can be used to solve it.
f(4)=max{f(1)f(3), f(2)f(2)}
f(5)=max{f(1)f(4), f(2)f(3)}
...
f(n)=max{f(1)f(n-1), f(2)f(n-2), f(3)f(n-3), ..., f(i)(fn-i), ...} (0<i<=n/2)
#include <stdio.h>
int maxrope(int length){
if(length < 2){ //If the rope is less than two meters and cannot be cut, it is 0
return 0;
}
if(length == 2){ //If the rope is two meters, then 1 * 1
return 1;
}
if (length == 3){//If the rope is three meters, then 1 * 2
return 2;
}
if (length ==4){ //If the rope is four meters, then 2 * 2
return 4;
}
int *products = new int[length+1];
int max = 0;
int product = 0;
products[0] = 0; //If part of the rope is 0 m after cutting, it is 0
products[1] = 1;//If the cut part of the rope is 1 meter, it is 1 meter
products[2] = 2;//If part of the rope is 2m after cutting, the optimal solution is not to cut 2m
products[3] = 3;//If part of the rope is 3M after cutting, the optimal solution is not to cut 3M
for(int i = 4;i < length+1;i++){
max = 0;
for (int j = 1;j <= i/2;j++){
product = products[j] * products[i-j]; //Multiplication of j-meter optimal solution and i-j-meter optimal solution
if (product > max){
max = product;
}
}
products[i] = max;
}
return products[length];
}
int main(){
int length = 0;
printf("Please enter the length of the rope:");
scanf("%d",&length);
printf("The optimal solution of the rope cutting problem is:");
printf("%d",maxrope(length));
}

3. Kings and gold mines
Problem description
In one country, five gold mines have been discovered. The gold reserves of each gold mine are different, and the number of workers who need to participate in the excavation is also different. The total number of workers involved in mining is 10. Each gold mine is either fully dug or not dug, and half of the people cannot be sent to dig half of the gold mine. It is required to solve by program. In order to get as much gold as possible, which gold mines should be dug?

Problem solving ideas
We set the gold mine as N, the number of workers as W, the gold quantity of the gold mine as array G, and the labor quantity of the gold mine as array P.
State transition equation:

#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int Goldbest(int w,int length,int p[],int g[]){
int result[length+1][w+1]={0}; //result [number of gold mines] [number of workers]
memset(result,0,sizeof result);
for(int i = 1;i < length+1; i++){ //The i-th gold mine
for(int j=1;j < w+1; j++){ //w workers assigned
if(j < p[i-1]){ //If the number of workers assigned cannot meet the requirements of the i-th gold mine, result[i][j] continues the result of i-1 of the previous gold mine
result[i][j] = result[i-1][j];
}
else{ //If enough people are allocated, select the maximum value from (the gold obtained by allocating j people to the first i-1 gold mine) and (excluding the gold obtained by the remaining people to dig the first i-1 gold mine after meeting the number of people to dig the i-th gold mine)
result[i][j]=max(result[i-1][j],result[i-1][j-p[i-1]]+g[i-1]);
}
}
}
return result[length][w];
}
int main(){
int g[5] = {500,200,300,350,400};
int p[5] = {5,3,4,3,5};
int length = 5;
int w = 10;
printf("The most gold can be mined is%d gold",Goldbest(w,length,p,g));
}

4. Longest common subsequence
Problem description
Given two sequences X={x1,x2,..., xm} and Y={y1,y2,..., yn}, find the longest common subsequence of X and y.
For example: X={A,B,C,B,D,A,B}, Y={B,D,C,A,B,A}, then the sequence {B,C,A} is a common subsequence of X and Y. But it is not one of the longest common subsequences of X and Y. Sequence {B,C,B,A} is a common subsequence of X and Y, its length is 4, and it is the longest common subsequence of X and Y. Because X and Y have no common subsequences with a length greater than 4. Its other solution is {B,C,A,B}. The answer to this question is not unique.
Problem solving ideas
Based on the optimal substructure property of the longest common subsequence problem, the recursive relationship of the optimal value of the subsequence problem is established. Record the length of the longest common subsequence of sequences Xi and YJ with c[i][j]. Where, Xi={x1,x2,..., Xi}; Yj={y1,y2,…,yj}. When i=0 or j=0, the empty sequence is the longest common subsequence of Xi and YJ. Therefore, C[i][j]=0. In other cases, the recursive relationship can be established according to the properties of the optimal substructure as follows:
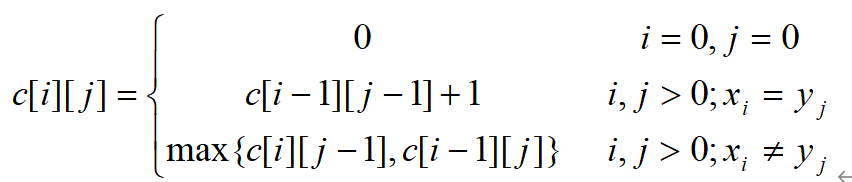
#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int main()
{
char x[50],y[50],z[50];
int l[51][51];
int k = 0;
while(scanf("%s %s",x+1,y+1)!=EOF){ //Enter two strings
memset(l,0,sizeof(l));
int m = strlen(x+1);
int n = strlen(y+1);
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++){
if(x[i]==y[j]){
l[i][j] = l[i-1][j-1]+1;
}else{
l[i][j] = max(l[i-1][j],l[i][j-1]);
}
}
printf("The length of the longest common subsequence is%d\n",l[m][n]);
}
return 0;
}
