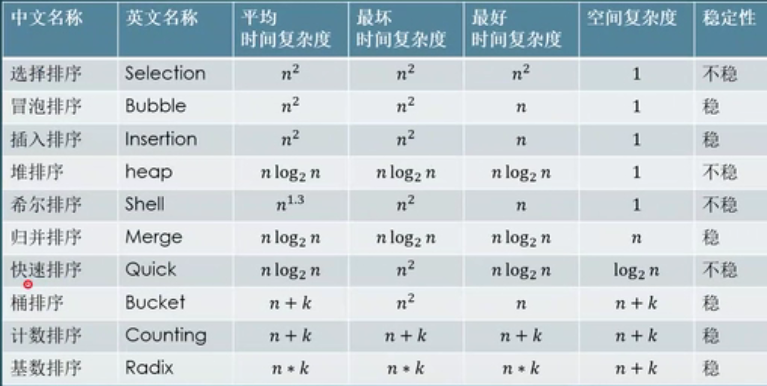
Memory formula: select bubbles and insert them. Go back to the bucket and count the base. EN Fang, en Lao, en wants to disperse, en Jia K, en multiply K. Unstable, unstable, unstable, unstable
How to debug a bug?: Read through program - > output intermediate value - > shear function. The core is positioning
Select sort:
Selection sorting is unstable because there is cross switching. The sorting method most in line with human thinking. From the first position to the last position, each position should be compared with the number in the back. If there is a smaller one in the back, take it.
//Select sort
for (int i = 0; i < array.Length - 1; i++)
{
for (int j = i + 1; j < array.Length; j++)
{
if (array[j] < array[i])
{
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}
}Bubble sort:
Different from selection sorting, first of all, the comparison object is the "every adjacent" element; Secondly, the optimal time complexity is O(n)
//Bubble sorting
bool swapHappend = false;
for (int i = array.Length - 1; i > 0; i--)
{
swapHappend = false;//The default value needs to be reset before each bubble starts.
for (int j = 0; j < i; j++)
{
if (array[j] > array[j + 1])
{
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
swapHappend = true;
}
}
if (!swapHappend) //When there is no exchange once, it proves that it has been arranged
{ //At this time, the time complexity can reach the optimal: O(n)
return;
}
}Insert sort:
For the basic ordered array, it is best to use, stable. Performance is better than bubble sorting. Insert the sorted array. In the sorting process, a segment is ordered (e.g. 1, 2, 3, 4, 5, 9, 7, 11, 56, 42, 33). Compare the elements at the unordered end with the ordered end, find the position of the unordered element at the ordered end, and then insert it (the above array is that element 7 is inserted between 5 and 9), The advantage of insertion sorting algorithm is that the loop can be stopped after finding the first insertable position.
//Insert sort
for (int i = 1; i < array.Length; i++) //Traverse forward from the second position
{
for (int j = i; j > 0; j--)
{
//Because the front part of the array is ordered, the first non insertable position is encountered
//You can stop comparing
if (array[j - 1] > array[j])
{
int temp = array[j - 1];
array[j - 1] = array[j];
array[j] = temp;
}
else
{
break;
}
}
}Hill sort:
Insert an improved version of sorting, using the idea of grouping. Compared with insertion sorting, first of all, it should be noted that there is one more loop, which is used to generate interval array; Secondly, it should be noted that the implementation of grouping mainly depends on the condition setting of the for loop, and the boundary is easy to make mistakes.
//Shell sort
//Calculate Knuth sequence as interval
int h = 1;
while (h < array.Length / 3)
{
h = 3 * h + 1;
}
//Start Shell sort
for (int gap = h; gap > 0; gap = (gap - 1) / 3)
{
for (int i = gap; i < array.Length; i++)
{
for (int j = i; j > gap - 1; j -= gap)
{
if (array[j] < array[j - gap])
{
int tempNum = array[j - gap];
array[j - gap] = array[j];
array[j] = tempNum;
}
else
{
break;
}
}
}
}Merge sort:
Recursion is used. Recursion needs to consider a bottom, that is, the case of recursive call to the last layer.
//Merge sort function
static void mergeSort(int[] array, int aHead, int aTail)
{
/*Parameter description
arayOutput: Original array aHead: array header pointer
aTail: Array tail pointer aMiddle: marker pointer that splits into two arrays
*/
if (aHead == aTail) { return; } //When there is only one element, returns
int i = (aHead + aTail) / 2; //Original array traversal pointer
int j = i + 1; //Original array traversal pointer
int[] arayOutputCopy = new int[aTail - aHead + 1]; //working space
int k = 0; //Workspace traversal pointer
mergeSort(array, aHead, i);
mergeSort(array, j, aTail);
if (array[i] <= array[j]) { return; } //Returns when the array is ordered
//Select the smaller element to put into the workspace
while (aHead <= i && j <= aTail)
{
if (array[aHead] <= array[j])
{
arayOutputCopy[k++] = array[aHead++];
}
else
{
arayOutputCopy[k++] = array[j++];
}
}
//Traverse the data that has not been traversed once
while (aHead <= i)
{ arayOutputCopy[k++] = array[aHead++]; }
while (j <= aTail)
{ arayOutputCopy[k++] = array[j++]; }
//The final result is assigned to the original array
for (int l = arayOutputCopy.Length - 1; l >= 0; l--, aTail--)
{ array[aTail] = arayOutputCopy[l]; }
}Quick sort:
It is easy to bug, and extreme cases need to be verified, including the case that the number used to determine the comparison is at the boundary of the array, the number of repetitions, and there are only two numbers. For the understanding of fast platoon, refer to the blog Simple quick sort_ Idle pen - CSDN blog_ Simple quick sort , in this blog, "throwing stones - > determining dirty data - > moving" is helpful for memorizing the algorithm. I first saw the quick sorting here in Yan Weimin's textbook of c language data structure. In addition to the "stone throwing method" to realize single axis fast discharge, there are other ways to realize it.
static void QuickSortIterative(int[] array, int Low, int High)
{
if (Low < High)
{
int pivot = QuickSort(array, Low, High);
QuickSortIterative(array, Low, pivot-1);
QuickSortIterative(array, pivot+1, High);
}
}
static int QuickSort(int[] array, int Low, int High)
{
int pivot = array[Low];
while (Low < High)
{
while (Low < High && array[High] >= pivot )
{ --High; }//The end of the loop indicates that the number on the right is found on the left (HIGH), or the traversal is completed
array[Low] = array[High];
while (Low < High && array[Low] <= pivot)
{ ++Low; } //The end of the loop indicates that the left number is found on the right (LOW), or the traversal is completed
array[High] = array[Low];
}
array[High] = pivot;
return Low;
}DualPivotSort:
The algorithm is the solution of the Dutch flag problem. There are three pointers in the double axis fast row, two of which are slow pointers, which are used to mark the positions of the two axes and divide the array into three areas; A fast pointer is used to traverse the array, one element at a time, to determine which of the three regions should be in. The execution code of different regions is not allowed, which is affected by the moving direction of the fast pointer.
public static void DualPivodSortIterative(int[] array, int low, int high)
{
if (low < high) {
int[] pos = DualPivodSort(array, low, high);
DualPivodSortIterative(array, low, pos[0]-1);
DualPivodSortIterative(array, pos[0] + 1, pos[1] - 1);
DualPivodSortIterative(array, pos[1] + 1, high);
}
}
public static int[] DualPivodSort(int[] array, int low, int high)
{
//Make the first axis < = the second axis
if (array[low] > array[high]) { swapArray(array, low, high); }
//Record the position of the shaft
int pivot1 = low;
int pivot2 = high;
//Working pointer middle
int middle = low + 1;
//There are three cases, so if has three branches, and the traversal direction is low - > high, so the second if does not need middle++
while (middle < high)
{
if (array[middle] < array[pivot1]) {
swapArray(array, ++low, middle++);
}
else if (array[middle] > array[pivot2]) {
swapArray(array,--high,middle );
}
else { middle++; }
}
//After traversing, return the axis to the axis position so that the left side of the axis is smaller than the axis and the right side of the axis is larger than the axis
swapArray(array,pivot1,low);
swapArray(array,pivot2,high);
int[] pos = { low, high };
return pos;
}Improvement of two axis quick sorting:
Two axis quick sort_ Idle pen - CSDN blog_ Double axis fast exhaust , the original three cases are judged and improved.
......
while (middle < high)
{
if (array[middle] < array[pivot1])
{
swapArray(array, ++low, middle);
}
else if (array[middle] > array[pivot2])
{
high--;
if (array[high] < array[low])
{
low++;
swapArray(array, high, middle);
swapArray(array, middle, low);
while (low + 1 < high && array[low + 1] < array[pivot1]) {
middle = ++low;
}
}
else if (array[pivot1] <= array[high] && array[high] <= array[pivot2]) {
swapArray(array, middle, high);
}
while (high - 1 >= middle && array[high - 1] > array[pivot2]) {
high--;
}
}
middle++;
}
......Heap sort:
Heap sorting requires pre knowledge reserves: "array storage method of complete binary tree", "non leaf node points and leaf node points are obtained from the points summarized by complete binary tree"
//Sorting function, first build a large top heap, and then cycle the process of "picking the top - > building a new heap"
static void HeapSort(int[] array)
{
//Large top heap construction, traversing from the last non leaf node at the bottom to the root node
//The traversal order and starting point cannot be changed, otherwise the HeapConstruct function needs to be rewritten
for (int i = array.Length / 2 - 1; i > -1; i--)
{
HeapConstruct(array, i, array.Length);
}
//Sort, that is, the "top picking process", and take the root node (node maximum) and the node at the last position every time
//After the exchange, we will determine the sorting position of a node, and the total number of nodes in the tree will be reduced by 1
//After the topping is completed, the total number of tree nodes is reduced, and the large top heap is also damaged. Therefore, it is necessary to start from the root node
//Traversal makes the binary tree into a large top heap again
for (int j = array.Length - 1; j > 0; j--)
{
swapArray(array, j, 0);
HeapConstruct(array, 0, j);
}
}
//Build a large top heap, and the input parameters are: the array storing the binary tree, the starting node, and the total number of nodes
static void HeapConstruct(int[] array, int node,int nodeNum)
{
int pointer = node; //Traversal pointer
//If the current pointer node is "non leaf node", the loop is executed
while (pointer < nodeNum / 2)
{
int tempPointer = pointer; //Current pointer backup
int sonL = pointer * 2 + 1; //Left child of current pointer node (non leaf node of complete binary tree, left child must exist)
int sonR = pointer * 2 + 2; //Right child of current pointer node (not necessarily exist)
//The right child exists and is a large value
if (sonR < nodeNum && array[sonL] < array[sonR]){
pointer = sonR;
}else { //Only the left child exists, or the left child is a larger value
pointer = sonL;
}
//If the value of the child node is greater, it will be exchanged, otherwise the traversal will be terminated
if (array[tempPointer] < array[pointer]) {
swapArray(array, tempPointer, pointer);
}else {
break;
}
}
}Count sort:
It is applicable to large amount of data but small data range. Such as the age ranking of tens of thousands of employees in large enterprises, and quickly knowing the ranking of the college entrance examination.
It belongs to non comparison sort.
First, determine that the data range of this group is 0~k and the amount of data is n. Assign k +1 positions to count the number of occurrences of 0 to K in this group of data.
Then you can simplify the counting sorting: make its spatial complexity (k), but this will make the sorting algorithm unstable
Counting and sorting will use the cumulative array, which contains two information: the number of occurrences and the position information of the number. At this time, the counting sorting can be stable, and its spatial complexity is inevitably (n+k).
//Count sort
//You need to know the min,max of this group
static void CountSort(int[] array, int min, int max)
{
int k = max - min + 1; // How many min~max in total
int[] countArray = new int[k]; // Count array
int[] sortedArray = new int[array.Length]; //Auxiliary array
//Traverse the original sequence to generate a count array (including count information)
for (int i = 0; i < array.Length; i++)
{
countArray[array[i] - min]++;
}
//Traverse the count array to generate the cumulative count array (including count information and location information)
for (int j = 1; j < k; j++)
{
countArray[j] = countArray[j] + countArray[j - 1];
}
//The original sequence array is traversed from back to front, because the position information contained in the count array is accumulated
//Is the location information of the last element in the "similar" element in the original sequence, such as the original sequence
//It contains three 1s. Although the three 1s are equal in size, their positions are different according to
//Position can distinguish elements into 1_A, 1_B, 1_C. The cumulative count array contains location information
//Yes, but the inclusion is 1_ The location information of C can only traverse the original sequence from back to front, and then according to
//The stability of the sorting algorithm can be guaranteed only by putting the elements in the sequence into the correct position in the cumulative count array
//Otherwise, the stability will be lost and the sequence "1_A, 1_B, 1_C" will become:
//"1_C, 1_B, 1_A"
for (int l = array.Length - 1; l >= 0; l--)
{
sortedArray[countArray[array[l] - min] - 1] = array[l];
countArray[array[l] - min]--;
}
//The data in sortedArray is ordered and assigned to array
for (int m = 0; m < array.Length; m++)
{
array[m] = sortedArray[m];
}
}Cardinality sorting:
Cardinality sorting is very similar to counting sorting, which is "non comparison" and "classification".
We need to find out the maximum value of the original sequence to determine the number of cardinalities. Assuming that the maximum is 1000, the number of cardinal numbers is 4, and the four cardinal numbers are "thousands, hundreds, tens and hundreds".
We start with bits and use the "cumulative count array" to sort the original array according to the size order of bits, and we need to ensure the stability. Then cycle the "base quantity" times and sort the remaining "ten", "hundred" and "thousand" logically.
The reason to start with a single bit rather than a thousand bits: you need to start with a base with little influence, otherwise you need to use recursion.
//Cardinality sort
static void RadixSort(int[] array)
{
//Generate auxiliary array for sorting
int[] helpArray = new int[array.Length];
//Find out the maximum value of the original sequence, so as to ensure that there are several cardinal numbers in total
int max = 0;
for (int i = 0; i < array.Length; i++) {
if (array[i] > max) {
max = array[i];
}
}
//Cycle to determine the cardinality quantity, that is, determine the total number of digits of the maximum value
int radixNum = 0;
while (max != 0) {
max /= 10; radixNum++;
}
//Cycle base quantity times
for (int j = 1; j <= radixNum; j++)
{
//Generate count array
int[] countArray = new int[10];
for (int k = 0; k < array.Length; k++) {
int radix = (int)(array[k] % Math.Pow(10, j) / Math.Pow(10, j - 1));
countArray[radix]++;
}
//Convert count array to cumulative count array
for (int l = 1; l < countArray.Length; l++) {
countArray[l] = countArray[l] + countArray[l - 1];
}
//Similar to counting sorting, traverse the original sequence from back to front
for (int m = array.Length - 1; m >= 0; m--) {
int radix = (int)(array[m] % Math.Pow(10, j) / Math.Pow(10, j - 1));
helpArray[countArray[radix] - 1] = array[m];
countArray[radix]--;
}
//So far, helpArray has stably sorted the original sequence according to the cardinality size,
//The sorted array is assigned to the original sequence
for (int n = 0; n < array.Length; n++) {
array[n] = helpArray[n];
}
}
}Bucket sorting:
Counting sort and cardinality sort are essentially bucket sort.