Learning from: https://labuladong.gitee.io/algo/3/25/85/

1, 0-1 knapsack problem

Give you a backpack with a weight of W and N items. Each item has two attributes: weight and value. Among them, the weight of the ith item is wt[i], and the value is val[i]. Now, what is the maximum value of the item you can pack with this back?



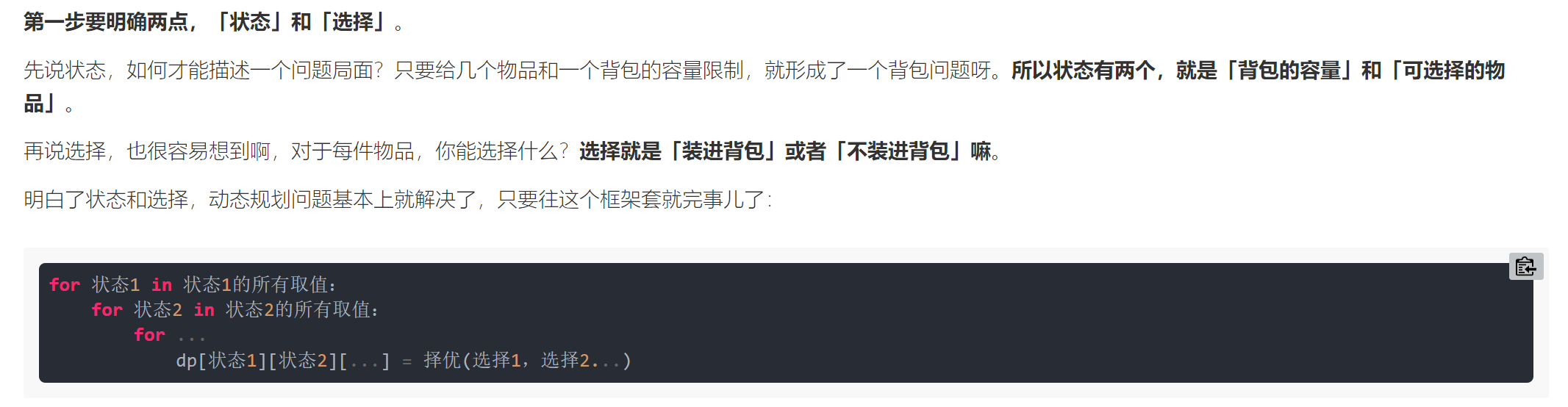
It should be noted that the meaning of DP array is because we need to describe the nature of the backpack: number of items + weight, so we have to use two-dimensional DP array to describe it. dp[i][j] represents the maximum value of the first I items that can be loaded when the backpack capacity is j.

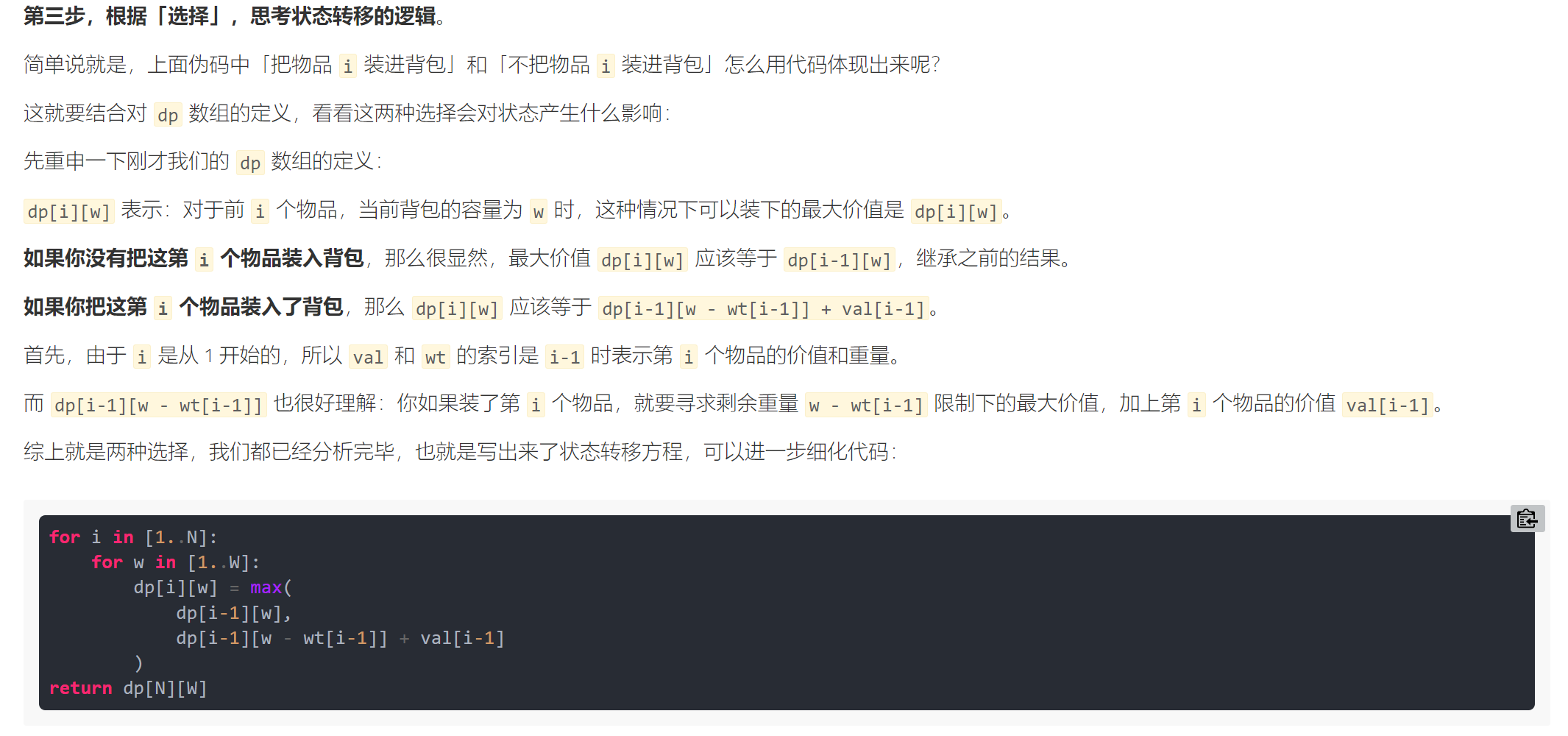
Let's look at the state transition equation. For each item, there are two states, loading it or not. In these two cases, we need to take the maximum value, dp[i][j]= max(dp[i - 1][j], dp[i - 1][j - wt[i]] + val[i]).

base case: when the number of items = 0 or the current capacity of the backpack = 0, the value = 0.

1.1 digital combination (simple)

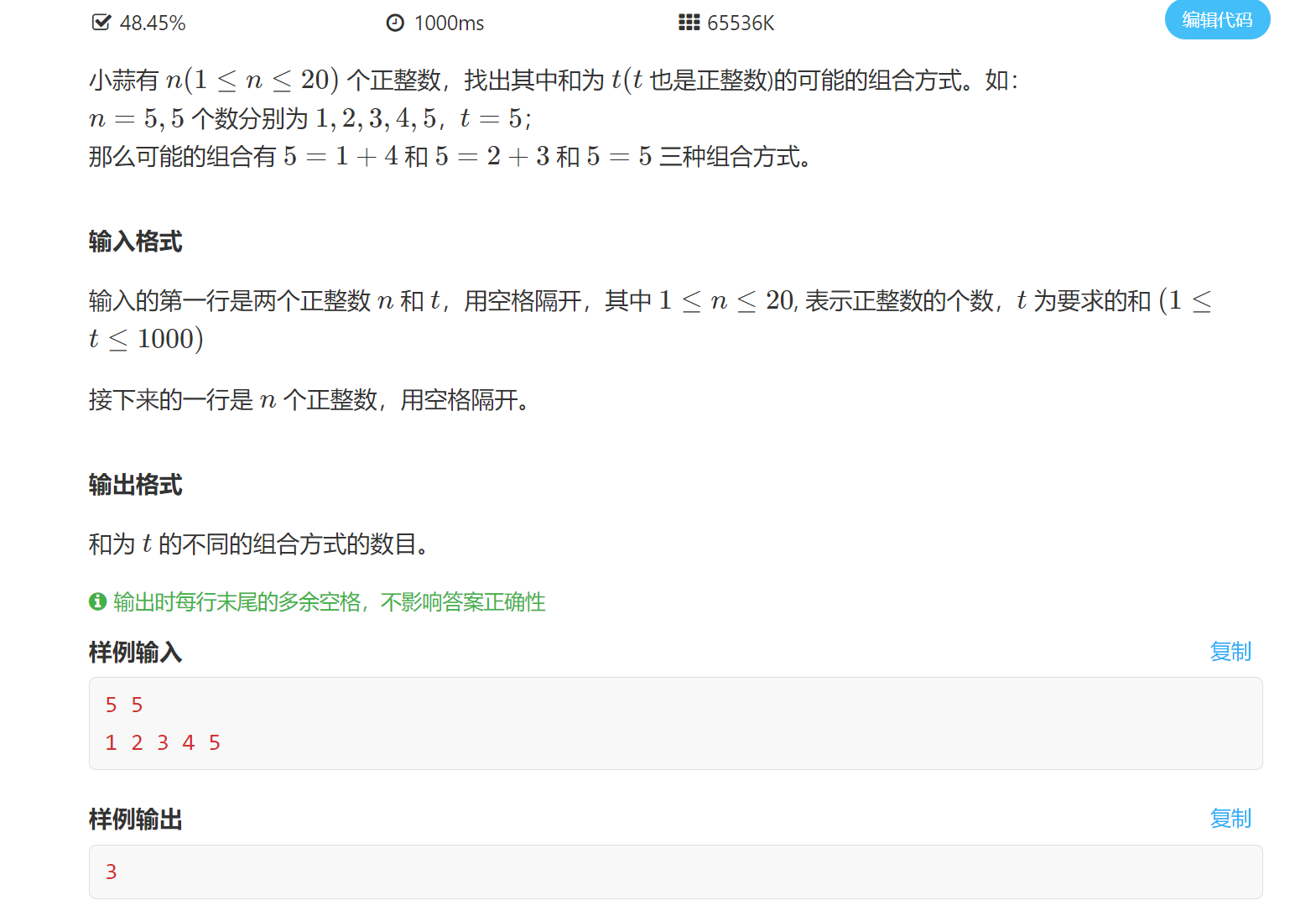
First, consider whether to use one-dimensional array or two-dimensional array. Because it is necessary to record the number of integers and the sum that needs to be rounded up, we choose two-dimensional array, dp[i][j] represents the first I number, and the sum is j.

Consider the case where the sum is 0, then for all I, dp[i][0] = 1, no number is taken, and one case can be rounded up to 0 (the given numbers are positive integers, and each number can only be used once).

The state transition equation has two states for a number: take it or not. The result we need should be the sum of the two cases, because it can be summed up if we take it or not, which belongs to different cases. dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]. If num [i] is greater than j, the current DP [i] [J] can only depend on the previous DP [I - 1] [J].

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        int n, t;
        Scanner scan =  new Scanner(System.in);
        n = scan.nextInt();
        t = scan.nextInt();
        // dp[i][j], the number of the first I, and the combination of j
        // There are two states for the current number: select it and deselect it
        // dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]
        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
            nums[i] = scan.nextInt();
        }
        int[][] dp = new int[n + 1][t + 1];
        // No matter how many numbers there are, if the number to be rounded up = 0, the combination method = 1
        for (int i = 0; i <= n ; i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= t; j++) {
                if (nums[i - 1] <= j) {
                    dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        System.out.println(dp[n][t]);
    }
}

1.2 segmentation and subsets (medium)

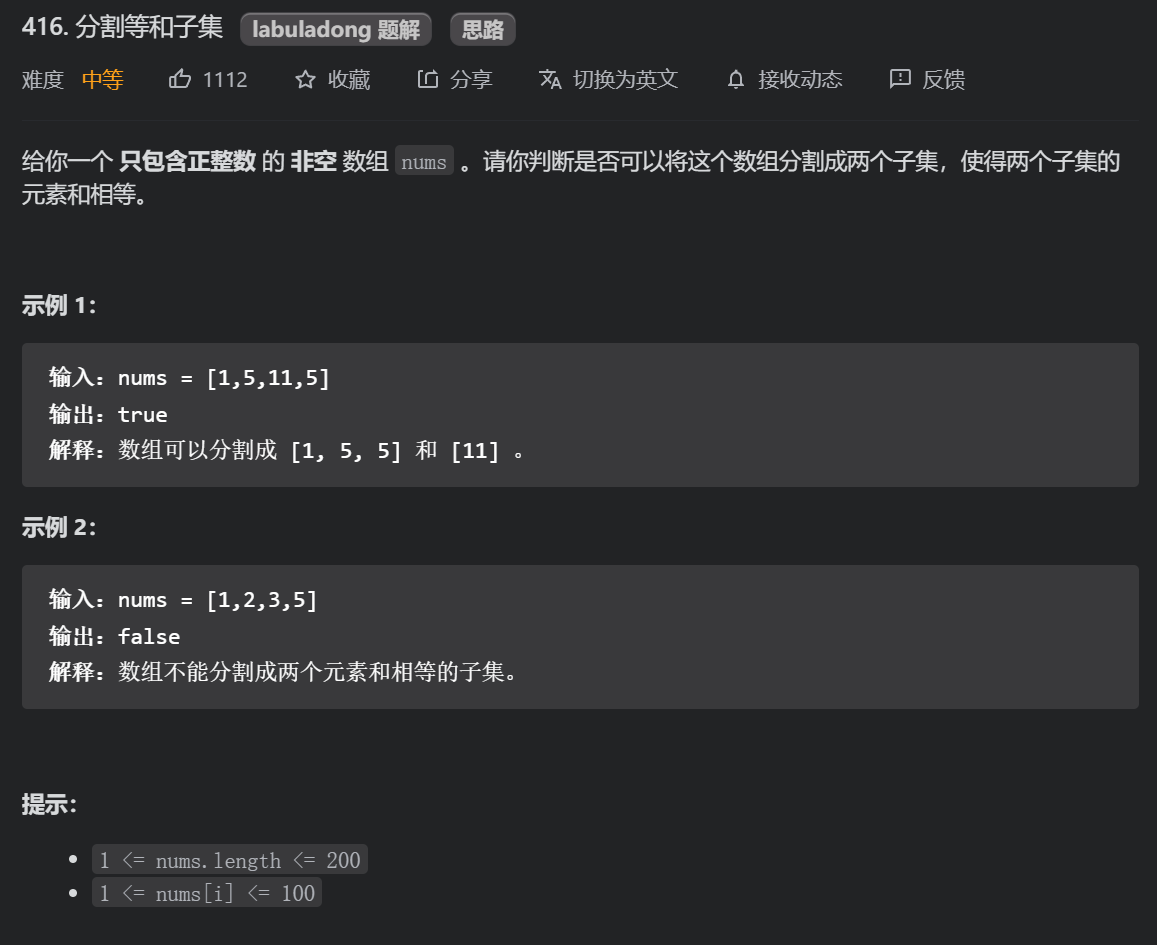
Divide into two subsets with equal sum (only positive integers). Then the sum of the two subsets = sum (Num) / 2. We only need to judge whether num can get sum / 2. Once it can, the other subset can also, because the sum of the array is fixed.

Because the number and subset sum of numbers need to be stored, a two-dimensional DP array is required, dp[i][j]. Can the first I numbers be summed to j.

dp[i][0], for all I, it is true, and 0 can be rounded up.

DP [i] [J] = DP [I - 1] [J] | DP [I - 1] [J - nums [i]], because for a number, we can take or not, we only need to make j, so we may not take it to make it, or we can make it.

When num [i] > J, dp[i][j] = dp[i - 1][j], the current number can only be left unchecked.

class Solution {
    public boolean canPartition(int[] nums) {
        // It is divided into two piles. The sum of each pile is the same
        int sum = 0;
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            sum += nums[i];
        }
        // And are odd, impossible
        if (sum % 2 != 0) {
            return false;
        }
        sum /= 2;
        // It is similar to the 0-1 knapsack problem, but sum/2 must be found here
        // If sum/2 can be obtained from the first n numbers, sum/2 can also be obtained from another subset
        boolean[][] dp = new boolean[n + 1][sum + 1];
        // dp[i][j] refers to the number of the first I. can we get j
        for (int i = 0; i <= n; i++) {
            dp[i][0] = true;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= sum; j++) {
                if (nums[i - 1] <= j) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n][sum];
    }
}

1.3 weight of the last stone II (medium) (adaptation)

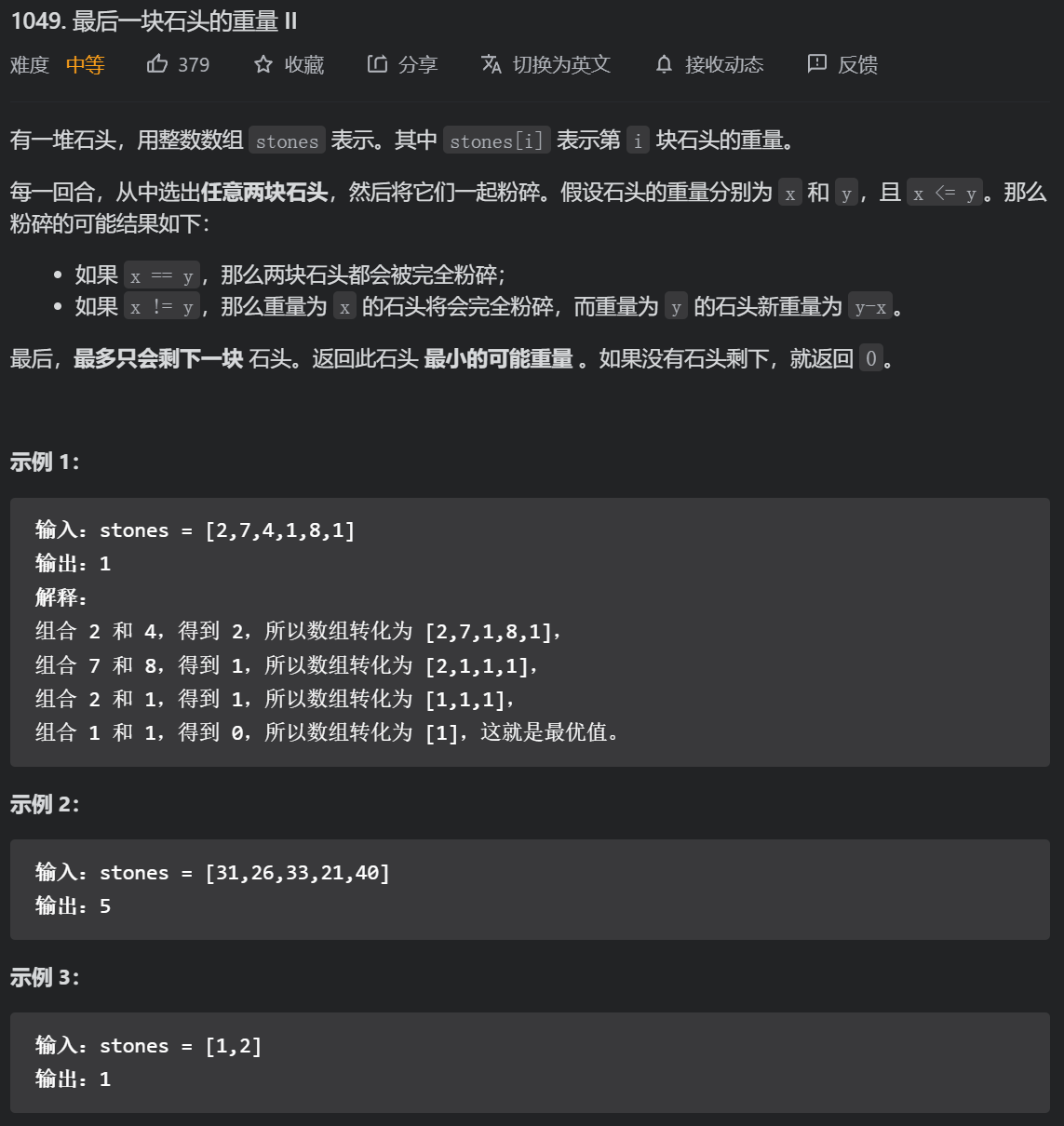
The overall concept is to divide the stones into two piles and minimize the difference between the two piles. How can we minimize it? Let's look at sum / 2 and try to make a pile of stones into sum / 2, so that the difference between another pile of stones is the smallest. So this question is the same as the previous one. You can think about this when you encounter problems in two piles. Choose two at a time, actually or in two piles.

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int n = stones.length;
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += stones[i];
        }
        int m = sum / 2;
        // Think as a whole and try to make the stone into half of the weight of the stone, so that the weight of the remaining half is the smallest
        // Smashing is equivalent to subtraction
        boolean[][] dp = new boolean[n + 1][m + 1];
        // dp[i][j] represents the number of the first I, can it be summed up into j (and)
        for (int i = 0; i <= n; i++) {
            dp[i][0] = true;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (stones[i - 1] <= j) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - stones[i - 1]];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        int max = 0;
        for (int j = 0; j <= m; j++) {
            if (dp[n][j]) {
                max = Math.max(max, j);
            }
        }
        return sum - max - max;
    }
}

1.4 ※ objectives and (medium)

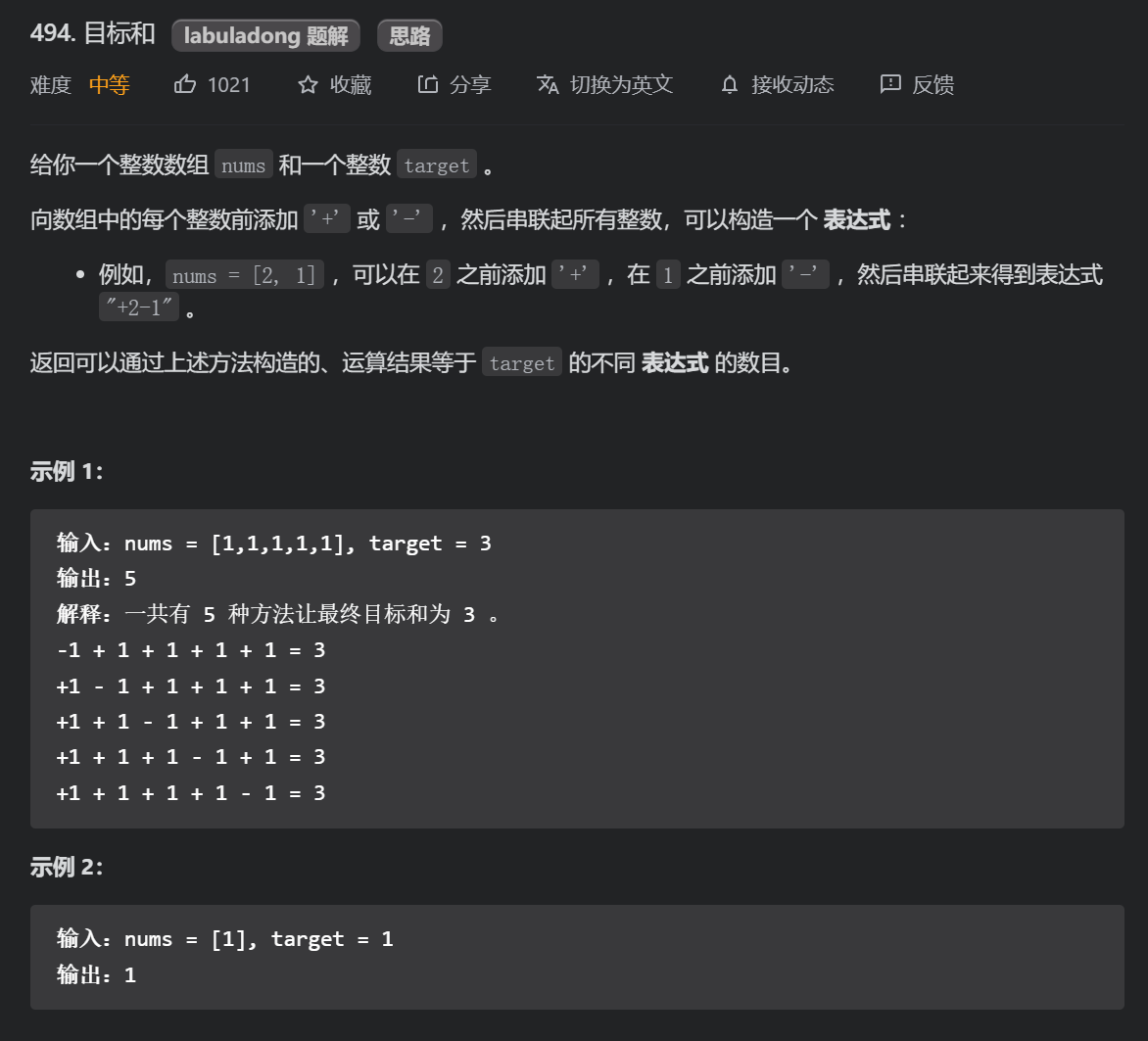
According to the idea of the previous topic, the whole set is divided into negative number set and positive number set. Assuming the sum of absolute values of negative numbers = neg, then the sum of positive numbers = sum - neg, sum - neg - neg = target, so neg = (sum - target) / 2. We only need to make the first n numbers add up neg, and the symbol of these numbers is -, The sign of the remaining number is +.

At the same time, note that neg cannot be less than 0 or decimal, so it returns 0 in both cases.

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        // If the sum of absolute values of negative numbers is neg, then the sum of positive numbers = sum - neg (note that num [i] is > = 0, but the target can be less than 0)
        // sum - neg - neg = target
        // neg = (sum - target) / 2
        int diff = sum - target;
        // The sum of the absolute values of negative numbers cannot be less than 0. At the same time, sum - target must be divisible by 2. If it cannot be divisible, it means it is a decimal, which cannot be a decimal
        if (diff < 0 || diff % 2 != 0) {
            return 0;
        }
        int n = nums.length, neg = diff / 2;
        int[][] dp = new int[n + 1][neg + 1];
        dp[0][0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= neg; j++) {
                if (j >= nums[i - 1]) {
                    dp[i][j] = dp[i - 1][j - nums[i - 1]] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n][neg];
    }
}

1.5 one and zero (medium) (normal Multidimensional 0-1 knapsack)

Finally, I met the normal 0-1 backpack problem. I don't have to turn my head and split it into two piles. It's not easy. Take a substring as an item, m and n are the capacity of the backpack. How many items can the backpack hold at a given capacity?

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        // Each binary string is treated as an item
        // The number of 0 and 1 is regarded as the capacity of the backpack  
        int len = strs.length;
        int[][][] dp = new int[len + 1][m + 1][n + 1];
        // dp[i][j][k], the maximum number of substrings that can be installed in the first I strings under the condition of m zeros and n ones
        for (int i = 1; i <= len; i++) {
            String tmp = strs[i - 1];
            int one = check(tmp);
            int zero = tmp.length() - one;
            // Note that the number of 0 and 1 starts to traverse from 0!
            for (int j = 0; j <= m; j++) {
                for (int k = 0; k <= n; k++) {
                    if (zero <= j && one <= k) {
                        // The topic is to find the longest length
                        dp[i][j][k] = Math.max(dp[i - 1][j - zero][k - one] + 1, dp[i - 1][j][k]);
                    } else {
                        dp[i][j][k] = dp[i - 1][j][k];
                    }
                }
            }
        }
        return dp[len][m][n];
    }
    static int check(String str) {
        int cnt = 0;
        for (int i = 0; i < str.length(); i++) {
            if (str.charAt(i) == '1') {
                cnt++;
            }
        }
        // Count the number of 1 in the string
        return cnt;
    }
}

Note that if the number of schemes and types required in the title is DP [I - 1] [J] + DP [I - 1] [J - num [i]], if the maximum value is max (DP [I - 1] [J], DP [I - 1] [J - num [i]] + Val [i])

2, Complete knapsack problem

There are N items and a backpack with a maximum weight of W. The weight of the ith article is weight[i], and the value obtained is value[i]. Each item has an infinite number (that is, it can be put into the backpack many times). Find out which items are put into the backpack, and the total value of the items is the largest.

The only difference between complete knapsack and 01 knapsack is that there are unlimited items of each kind.

1.6 change (medium)

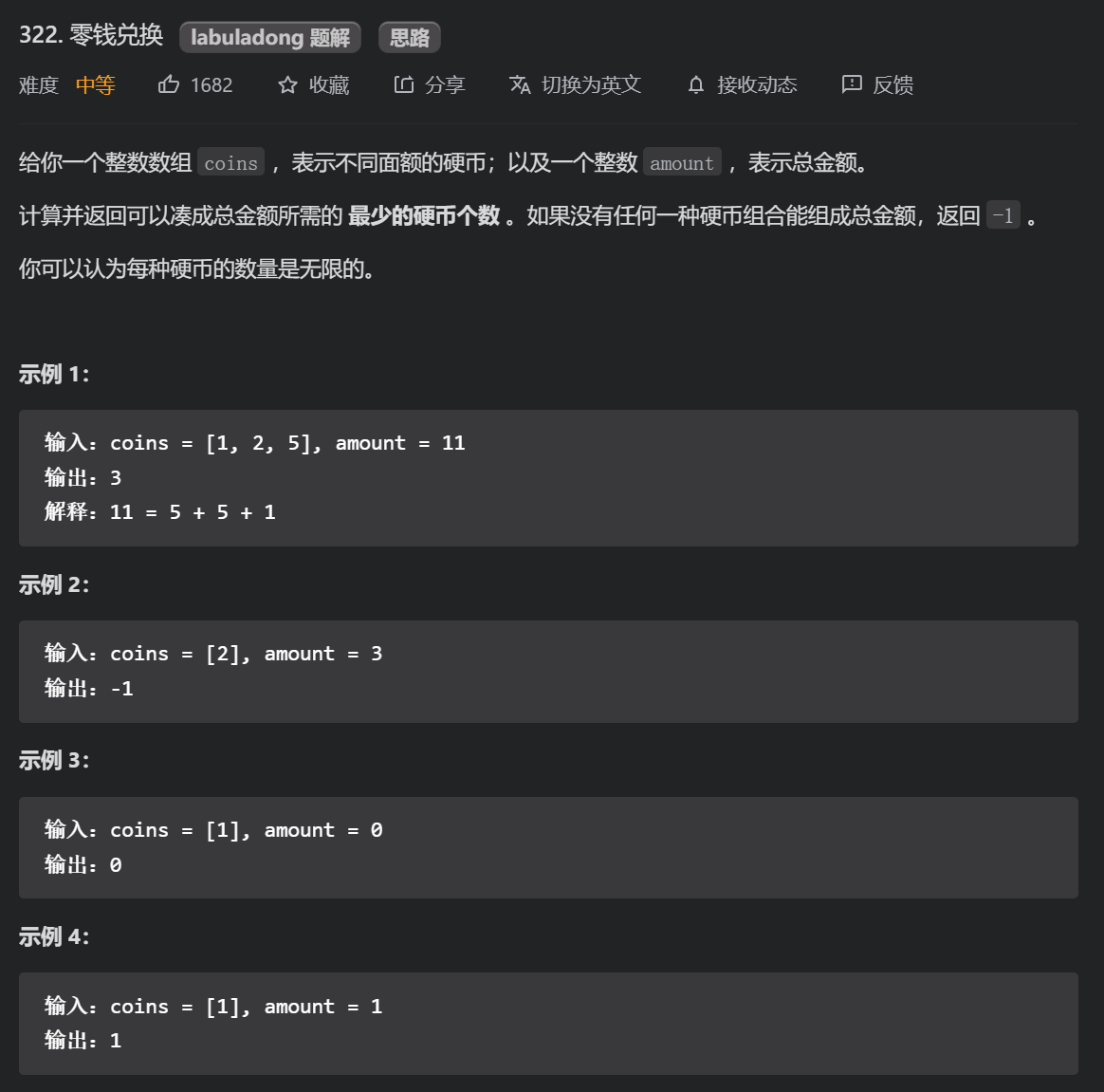
This problem is the complete knapsack problem. Coins can be reused. Be sure to pay attention to the difference between the state transition equation of 0-1 knapsack and complete knapsack: mainly when you can put down items
01 Back package : d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] ) finish whole Back package : d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − w [ i ] ] + v [ i ] ) 01 backpack: dp[i][j] = max(dp[i - 1][j], dp[i -1][j-w[i]]+v[i]) \ \ full backpack: dp[i][j] = max(dp[i - 1][j],dp[i][j-w[i]] + v[i]) 01 backpack: dp[i][j]=max(dp[i − 1][j],dp[i − 1][j − w[i]]+v[i]) full backpack: dp[i][j]=max(dp[i − 1][j],dp[i][j − w[i]]+v[i])
If the complete backpack can put down the i-th item, it can also choose to continue to put the i-th item instead of returning to the I - 1st item.

The minimum value is required in the title, so the array should be initialized to infinity, otherwise it will affect the subsequent state transition.

class Solution {
    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        // Complete backpack, dp[i][j], the minimum number of coins required for the first I coins to form j amount
        int[][] dp = new int[n + 1][amount + 1];
        // Because the minimum value needs to be filled in with the maximum value (note that the two-dimensional array needs to be filled in with for)
        for (int i = 0; i <= n; i++) {
            Arrays.fill(dp[i], amount + 1);
            // It only takes 0 coins to make up the amount
            dp[i][0] = 0;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= amount; j++) {
                if (j >= coins[i - 1]) {
                    // Note that when you can put it down, continue to consider i instead of i - 1
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - coins[i - 1]] + 1);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n][amount] == amount + 1 ? -1 : dp[n][amount];
    }
}

1.7 change II (medium)

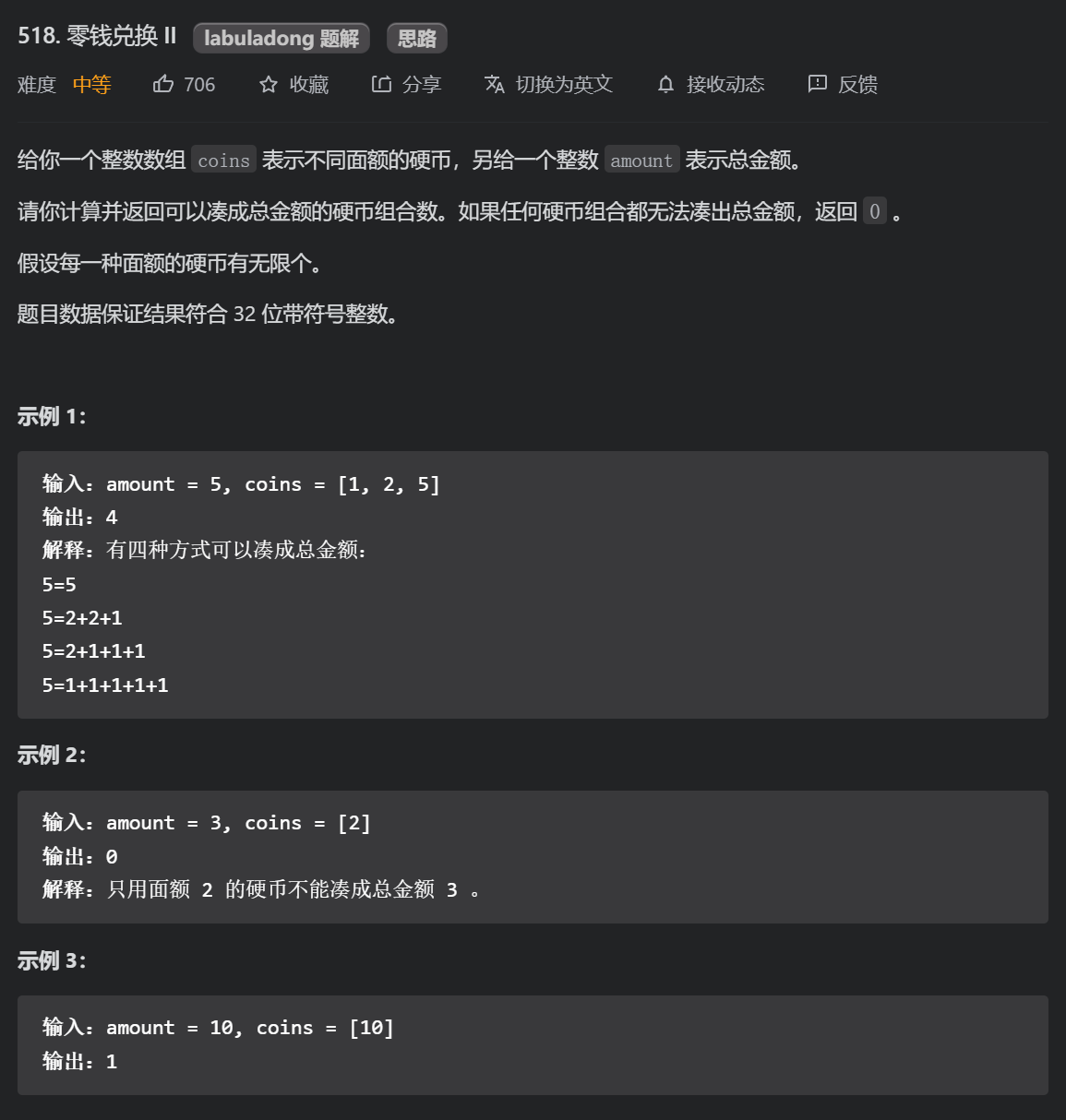
Like the previous question, it is a complete knapsack problem, but this question is about the number of schemes. Consider the amount J, dp[i][j] = dp[i - 1][j] + dp[i][j -coins[i]], because it may consist of the first i - 1 coin J. if it is a 01 backpack, dp[i -1][j - coins[i]] should be added after it. The i-th coin can only be used once, and the first i - 1 coin must be considered; But this is a complete knapsack. The i-th coin can be used all the time, so continue to consider whether the first I coins can be added up to j, which is dp[i][j - coinst[i]].

Finding the number of schemes is the sum of two states, and finding the extreme value is the max or min of two states. Remember to initialize the array to infinity when maximizing.

class Solution {
    public int change(int amount, int[] coins) {
        // Complete knapsack problem
        int n = coins.length;
        int[][] dp = new int[n + 1][amount + 1];
        // dp[i][j] the first I coins constitute the number of schemes of j amount
        // No matter how many coins there are, the scheme that makes up the amount of 0 is 1
        for (int i = 0; i <= n; i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= amount; j++) {
                if (coins[i - 1] <= j) {
                    // Note that it's a complete backpack
                    dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n][amount];
    }
}

1.8 buying books (simple)

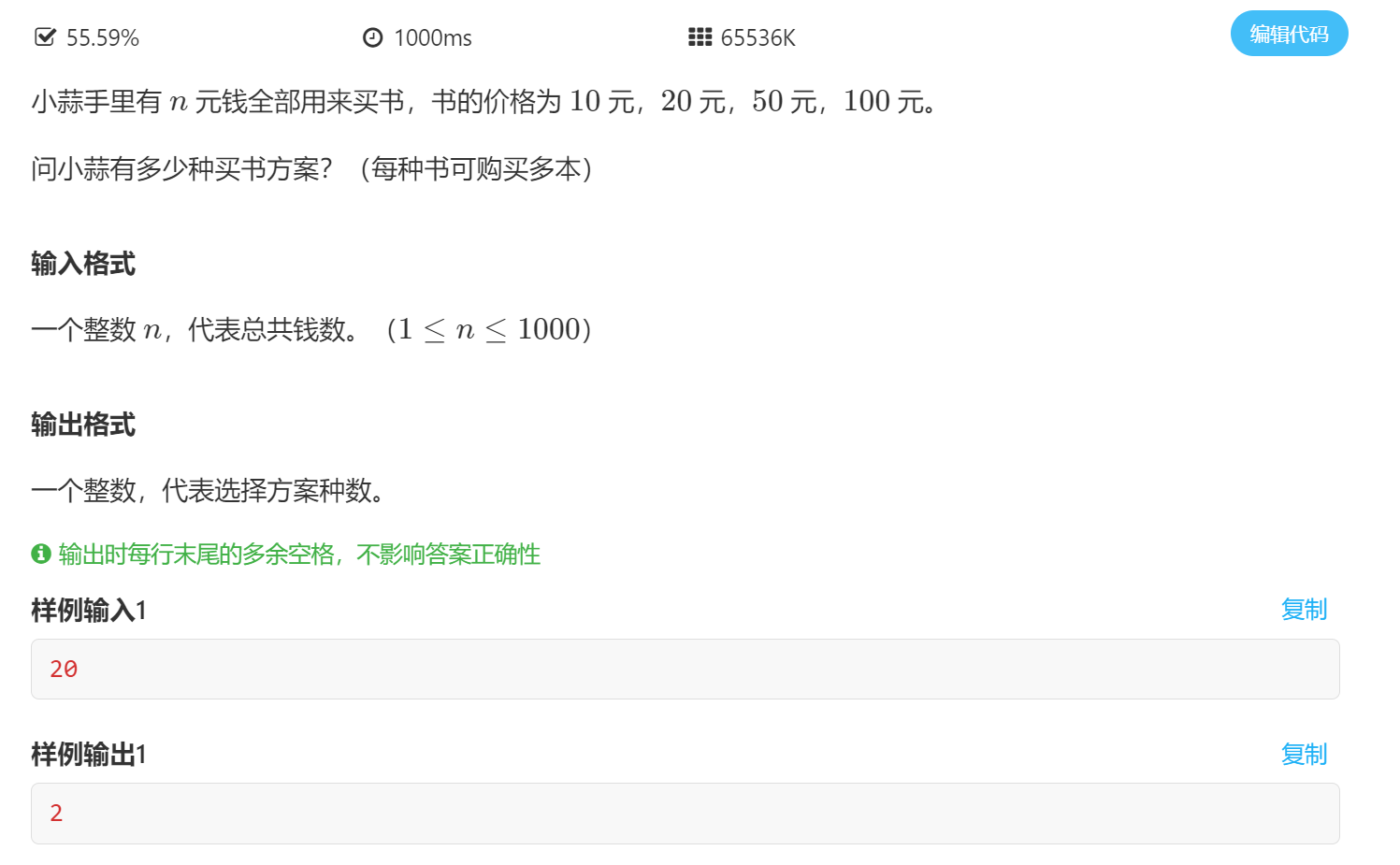
Or is it a complete knapsack problem? You can buy more books, and the money must be spent (all used to buy books). When you enter 15, the result is 0.

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        int n;
        Scanner scan =  new Scanner(System.in);
        n = scan.nextInt();
        // For the complete knapsack problem, finding the number of schemes is the addition of two states
        // Price of record book
        int[] price = new int[] {10, 20, 50, 100};
        int[][] dp = new int[5][n + 1];
        // dp[i][j], book purchase scheme when the amount of the first I book is j
        for (int i = 0; i <= 4 ; i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i <= 4 ; i++) {
            for (int j = 1; j <= n ; j++) {
                if (price[i - 1] <= j) {
                    // Complete backpack and can be transferred to i
                    dp[i][j] = dp[i - 1][j] + dp[i][j - price[i - 1]];
                } else {
                    // If you can't put the i - th book, look at the first i - 1 book
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        System.out.println(dp[4][n]);
    }
}

※ III. arrangement or combination?

1.9 ※ combined sum IV

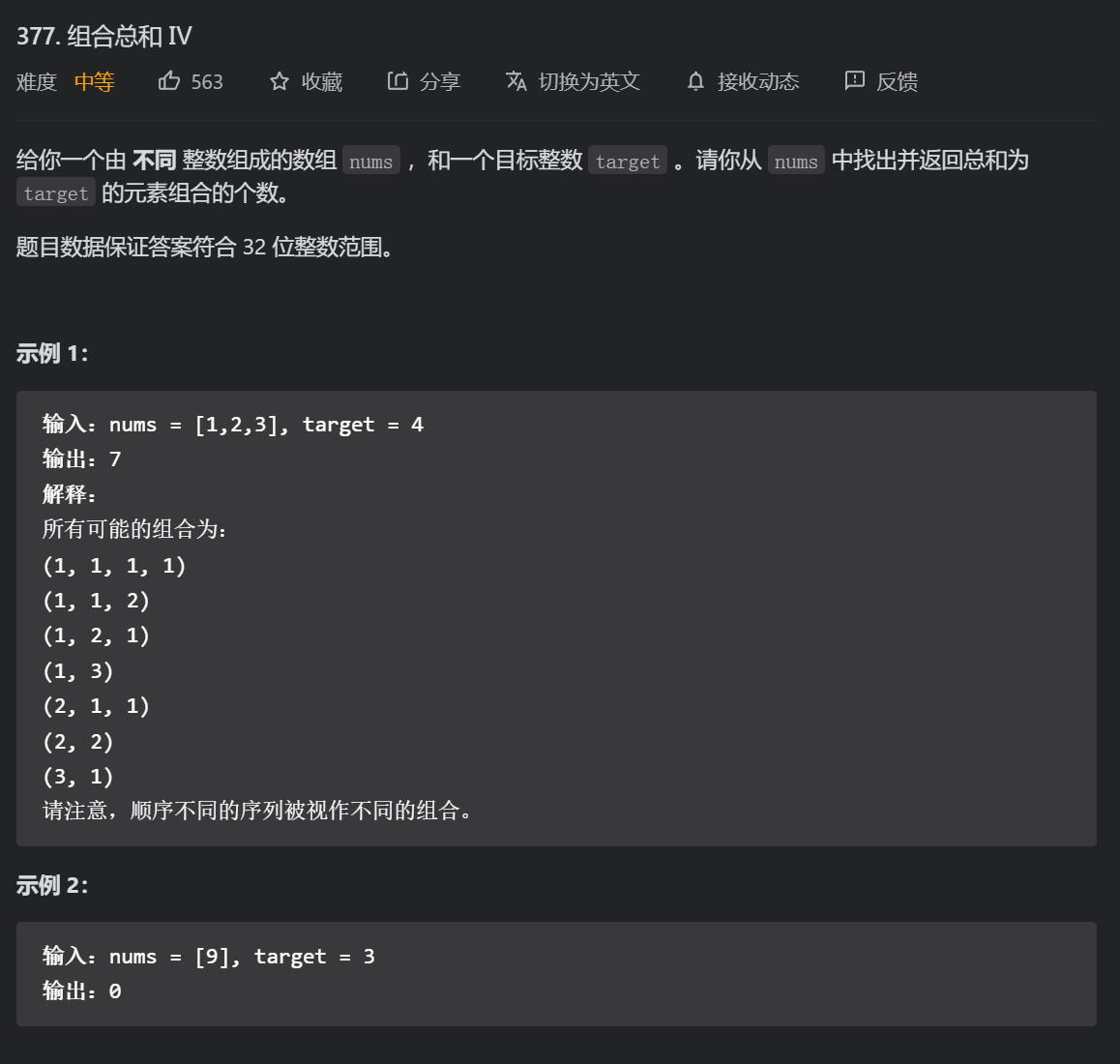
Given n numbers, given the target sum, the number can be taken infinitely, hey? Isn't it a complete backpack?

It's wrong to think so. This problem is a full permutation dynamic programming problem (permutation emphasizes different positions, and the combination does not consider different positions). It's not a complete knapsack problem at all (the problem solution is implemented with a one-dimensional array of complete knapsack problems, but it's a bit rigid). A better explanation is as follows:

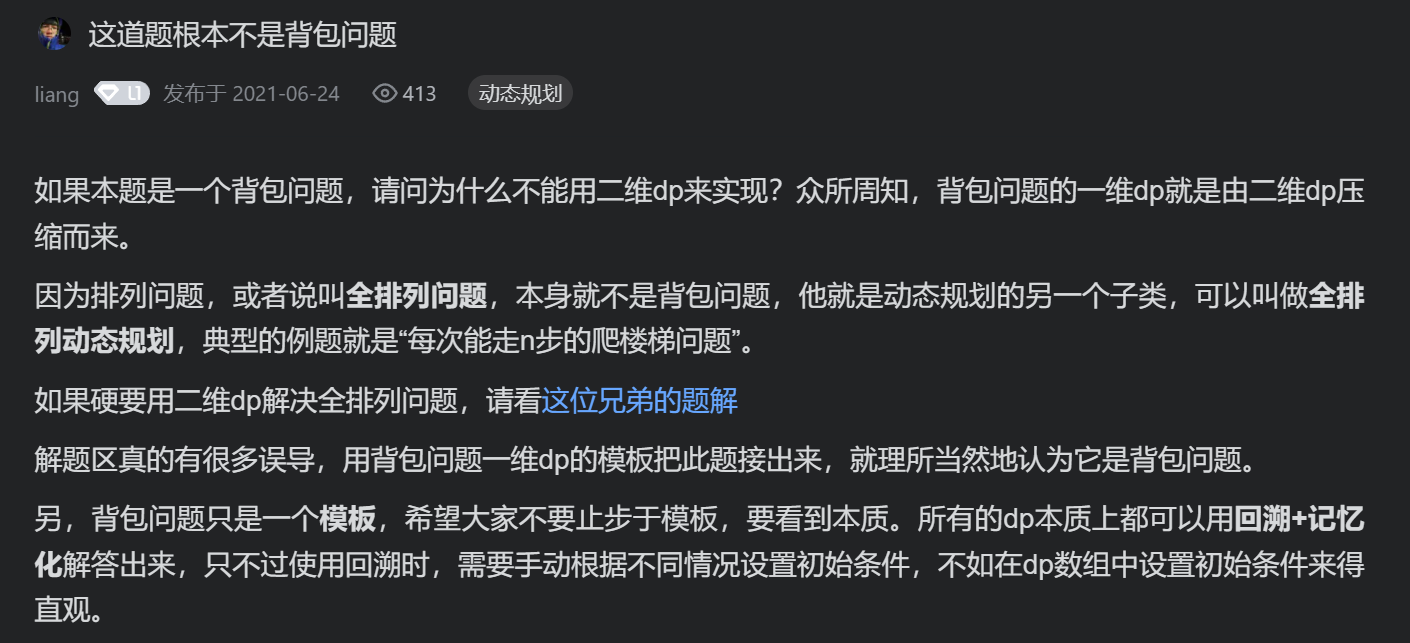
You can turn over the above questions. We are looking for combinatorial numbers, not permutation numbers!!!

First look at climbing stairs, and then go back to this problem to know how to do it!

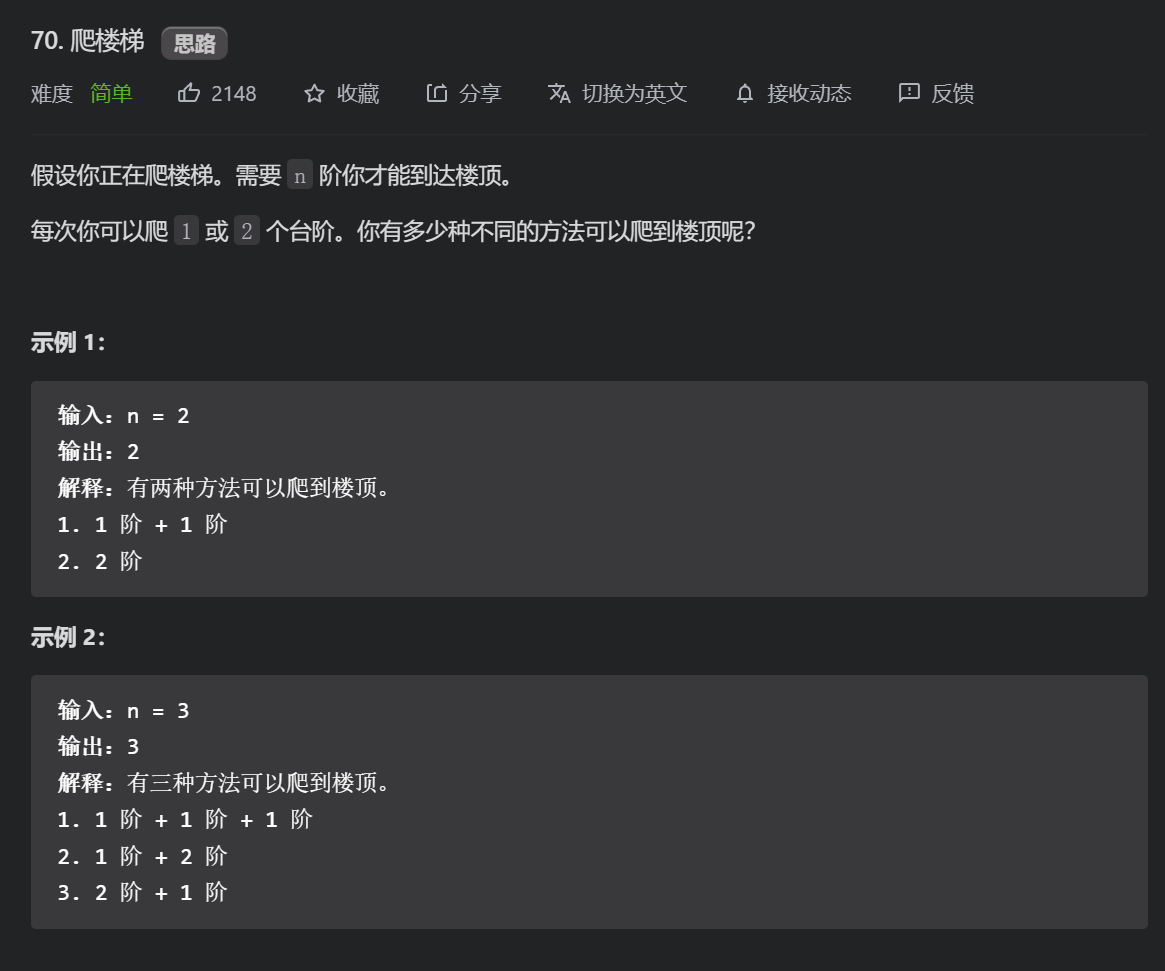
class Solution {
    public int climbStairs(int n) {
        if (n <= 2 ) {
            return n;
        }
        int[] ans = new int[n + 1];
        ans[1] = 1;
        ans[2] = 2;
        for (int i = 3; i <= n; i++) {
            ans[i] = ans[i - 1] + ans[i - 2];
        }
        return ans[n];
    }
}

Climbing to the nth step can be regarded as the sum of schemes climbing to the nth - 1 + nth - 2 steps.

The above is the solution using recursive formula, or the following method can be used:

class Solution {
    public int climbStairs(int n) {
        if (n <= 2 ) {
            return n;
        }
        int[] ans = new int[n + 1];
        ans[1] = 1;
        ans[2] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= 2; j++) {
                if (j <= i) {
                    ans[i] += ans[i - j];
                }
            } 
        }
        return ans[n];
    }
}

It's OK to climb the stairs from [J-i] to [target-nums], but it's OK to climb back to the top of the stairs!

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int n = nums.length;
        // It is similar to climbing stairs, but the number of steps you can take nums[i] at a time requires the target ladder to climb to the roof
        // Ask the number of schemes that can climb to the roof
        int[] dp = new int[target + 1];
        // For each possible number of steps to climb, there is at least one scheme
        // Of course, you can also directly make dp[0] = 1, and the result is the same as that
        for (int i = 0; i < n; i++) {
            if (nums[i] <= target) {
                dp[nums[i]] = 1;
            }
        }
        // The i-th step can be climbed up by the step of i - nums[j] + nums[j]!
        for (int i = 1; i <= target; i++) {
            for (int j = 0; j < n; j++) {
                if (nums[j] <= i) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}

Problems involving arrangement and combination generally require "number of types" in the title. If it is to find the maximum value, don't worry about this problem. It can be found by arrangement and combination. (there are fewer cases to consider when using combination, so it is generally combination. The combination problem is an ordinary complete knapsack problem. When encountering the problem of arrangement, you should learn to convert it to the problem of climbing stairs.)

4, 2D DP compression 1D DP

For the complete knapsack problem (combination problem), you can simplify the two-dimensional DP array into one-dimensional. This idea is actually felt when doing many questions, such as the initial change exchange problem. If you haven't learned complete knapsack, the direct idea is to declare a one-dimensional DP array, and dp[i] represents the combination mode of I amount (depending on whether the topic is arranged or combined).

For the one-dimensional DP array solution of the complete knapsack problem, we must pay attention to the order of internal and external traversal. If it is to find the maximum value, it will not affect the type and number of schemes.

I still prefer two-dimensional DP array for better understanding. There is no need to compress it into one-dimensional array, which is inconvenient to understand. We must remember these things and limit dynamic programming.

1.10 perfect square (medium)

This problem is a complete knapsack problem. Each complete square number can be taken multiple times. The knapsack capacity is n, and the items are complete square numbers. It belongs to the type of combination. One dimensional DP array should traverse the items first and then the knapsack capacity (that is, the most common case). Because it is the most value, the combination number and arrangement number can be calculated, and the traversal order will not be affected.

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        // dp[i] minimum number of integers i required
        Arrays.fill(dp, n);
        dp[0] = 0;
        for (int i = 1; i <= Math.sqrt(n); i++) { // Traverse items first
            for (int j = 1; j <= n; j++) {  // Then traverse the backpack
                if (i * i <= j) {
                    dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
                }
            }
        }
        return dp[n];
    }
}

The essence of compressing a two-dimensional DP array into a one-dimensional DP array is to remove the I of dp[i][j], that is, no items are stored, and only the backpack capacity is stored. However, during the for loop traversal, the items and backpacks should be traversed. The backpack capacity of 01 backpack should be traversed from large to small, and the backpack capacity of complete backpack should be traversed from small to large, and their items should be traversed from small to large, Note that when the internal and external loop traversal of the complete knapsack is different, one represents the number of combinations and one represents the number of permutations.

1.11 word splitting (medium)

This problem is also a complete knapsack problem, and is to find the number of permutations, because the s string requires the same order.
With one-dimensional DP, the outer layer traverses the backpack and the inner layer traverses the items.

class Solution {
        public boolean wordBreak(String s, List<String> wordDict) {
            // Words can be reused: complete knapsack problem
            // Item: each word, backpack: s
            int s_len = s.length();
            int size = wordDict.size();
            boolean[] dp = new boolean[s_len + 1];
            dp[0] = true;
            // First traverse the backpack and then traverse the items, because the words in the string have order requirements
            // Backpack can put down items, not only the size is appropriate, but also the string is equal!
            for (int i = 1; i <= s_len; i++) {  // knapsack
                for (int j = 1; j <= size; j++) {   // goods
                    int len = wordDict.get(j - 1).length();
                    if (i >= len && wordDict.get(j - 1).equals(s.substring(i - len, i))) {
                        dp[i] = dp[i] || dp[i - len];
                    }
                }
            }
        }
}

When solving difficult problems, the benefits of one-dimensional DP array can also be reflected. The problem is not a simple knapsack problem, but has multiple masks. At this time, one-dimensional DP array is better to deal with the problem.

5, Multiple Backpack

There are N items and a backpack with a capacity of V. There are up to Mi items available for item i, and the space consumed by each item is Ci and the value is Wi. Solve which items are loaded into the backpack, so that the total space consumed by these items does not exceed the backpack capacity, and the total value is the largest.

Multiple backpacks are very similar to 01 backpacks. Why are they similar to 01 backpacks?

There are at most Mi items available for each item. Spreading out Mi items is actually a 01 knapsack problem.

public void testMultiPack1(){
    List<Integer> weight = new ArrayList<>(Arrays.asList(1, 3, 4));
    List<Integer> value = new ArrayList<>(Arrays.asList(15, 20, 30));
    List<Integer> nums = new ArrayList<>(Arrays.asList(2, 3, 2));
    int bagWeight = 10;

    for (int i = 0; i < nums.size(); i++) {
        while (nums.get(i) > 1) { // Expand items into i
            weight.add(weight.get(i));
            value.add(value.get(i));
            nums.set(i, nums.get(i) - 1);
        }
    }

    int[] dp = new int[bagWeight + 1];
    for(int i = 0; i < weight.size(); i++) { // Traverse items
        for(int j = bagWeight; j >= weight.get(i); j--) { // Traversal knapsack capacity
            dp[j] = Math.max(dp[j], dp[j - weight.get(i)] + value.get(i));
        }
        System.out.println(Arrays.toString(dp));
    }
}