sketch

Recursive order (recursive access)
- Recursion: access order
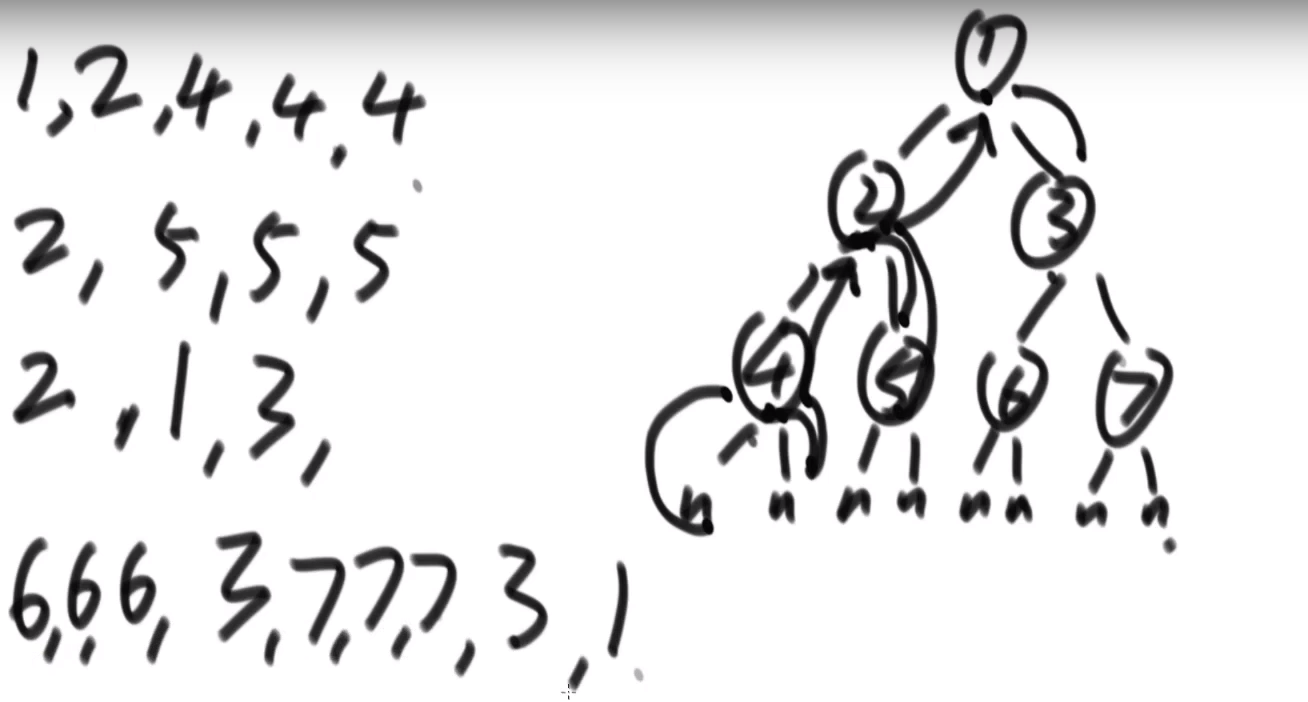
Recursive order: 1, 2, 4, 4, 2, 5, 5, 5, 2, 1, 3, 6, 6, 3, 7, 7, 7, 3, 1
First order: print the first time in the recursive order, and no operation during the second and third access: 1, 2, 4, 5, 3, 6 and 7
Middle order: print the second time in the recursive order, and no operation during the first and third accesses: 4, 2, 5, 1, 6, 3, 7
Post order: print when the recursive order appears for the third time. There is no operation during the first and second access: 4, 5, 2, 6, 7, 3, 1
public static void preOrderRecur(Node head){
if (head == null){
return;
}
System.out.println(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
public static void inOrderRecur(Node head){
if (head == null){
return;
}
inOrderRecur(head.left);
System.out.println(head.value + " ");
inOrderRecur(head.right);
}
public static void posOrderRecur(Node head){
if (head == null){
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.println(head.value + " ");
}
Non recursive access
- Non recursive: implemented by handwriting stack
1. Priority:
(1) Pop up a node from the stack
(2) Print (process) the node
(3) Press right then left (if any) into the stack (ensure that the stack is left and right)
(4) Repeat until the stack is empty
public static void preOrderRecur(Node head){
if (head != null){
Stack<Node> stack = new Stack<>();
stack.push(head);
while (!stack.isEmpty()){
Node p = stack.pop();
System.out.println(p.value);
if (p.right != null){
//Press in the right subtree first
stack.push(p.right);
}
if (p.left != null){
stack.push(p.left);
}
}
}
}
Sequence 2:
(1) The left boundary of each subtree is stacked
(2) Print (process) in the process of pop-up in turn, and pop up the right subtree (and its left boundary) of the node into the stack
(3) Repeat 1, 2
public static void inOrderRecur(Node head){
if (head != null){
Stack<Node> stack = new Stack<Node>();
Node p = head;
while (!stack.isEmpty() || p != null){
if (p != null){
stack.push(p);
p = p.left;
}else {
p = stack.pop();
System.out.println(p.value + " ");
p = p.right;
}
}
}
}
3. Post order: a collection stack is required
(1) Pop up a node from the stack
(2) Put the node into the collection stack (the parent node is at the bottom of the collection stack)
(3) Press left to right (if any) into the stack (ensure that the collection stack is right and left)
(4) Repeat until the stack is empty
(5) Print (process) collection stack (stack out is left, right, parent)
public static void preOrderRecur(Node head){
if (head != null){
Stack<Node> stack = new Stack<>();
Stack<Node> temp = new Stack<>(); //Collection stack
stack.push(head);
while (!stack.isEmpty()){
Node p = stack.pop();
temp.push(p); //Push into collection stack
if (p.left != null){
//Press in the left subtree first
stack.push(p.left);
}
if (p.right != null){
stack.push(p.right);
}
}
while (!temp.isEmpty()){
Node p = temp.pop();
System.out.println(p.value + " ");
}
}
}
Visual print tree
public static class Node{
int value;
Node left;
Node right;
public Node(int date){
//Constructor
this.value = date;
}
}
public static void printTree(Node head){
System.out.println("Binary Tree");
printInOrder(head, 0, "H", 12);
System.out.println();
}
public static void printInOrder(Node head, int height, String to, int len){
//head node
//height current depth
//to represents the relationship, H: head node; ↖: Indicates that the parent node is on its upper left; ↙: Indicates that the parent node is at its lower left
//The display length of len tree can be adjusted by itself
if (head == null){
return;
}
printInOrder(head.right, height + 1, "↙", len);
String val = to + head.value + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.left, height + 1, "↖" , len);
}
public static String getSpace(int num){
String space = " ";
StringBuilder buf = new StringBuilder(" ");
for (int i = 0; i < num; i++){
buf.append(space);
}
return buf.toString();
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(2);
head.right = new Node(3);
head.left.left = new Node(4);
head.left.right = new Node(5);
head.right.left = new Node(6);
head.right.right = new Node(7);
head.left.right.right = new Node(8);
head.right.right.left = new Node(9);
printTree(head);
}
Ideal diagram:

Rendering: H: head node; ↖: Indicates that the parent node is on its upper left; ↙: Indicates that the parent node is at its lower left

Topic 1: find the maximum width of the tree (breadth first)
level traversal
public static void levelOrder(Node head){
if (head == null){
return;
}
Queue<Node> queue = new LinkedList<Node>();
Node p = head;
queue.add(p);
while (!queue.isEmpty()){
p = queue.poll();
if (p.left != null){
queue.add(p.left);
}
if (p.right != null){
queue.add(p.right);
}
}
}
- Written test code:
(1) Idea: three values, the layer where the current node is located, the number of nodes in each layer, and the layer with the most nodes in the tree
(2) Implementation method: combined with hierarchical traversal, HashMap is used to bind each node to the corresponding layer. When leaving the queue, add one node to the number of corresponding layers, and finally find the layer with the most nodes
public static int levelMax(Node head){
if (head == null){
return 0;
}
Queue<Node> queue = new LinkedList<Node>();
int level = 1; //Number of layers
int levelNum = 0; //Number of nodes in this layer
int nodeMax = 0; //Maximum number of nodes
HashMap<Node, Integer> map = new HashMap<>();
Node p = head;
map.put(p, 1);
queue.add(p);
while (!queue.isEmpty()){
p = queue.poll();
if (map.get(p) == level){
//The current node layer is the same as the layer to be recorded
levelNum++;
}else {
//The current node layer is different from the layer to be recorded. Enter the next layer to update the data
nodeMax = Math.max(nodeMax, levelNum); //Maximum update
level++; //Layer number update
levelNum = 1; //Reset the node number of the corresponding layer
}
if (p.left != null){
map.put(p.left, level + 1);
queue.add(p.left);
}
if (p.right != null){
map.put(p.right, level + 1);
queue.add(p.right);
}
}
return nodeMax;
}
- Interview ideas:
(1) Idea: four values, the end node of the current layer, the next end node of the current layer, the number of nodes in each layer, and the layer with the most nodes in the tree
(2) Implementation method: in combination with hierarchical traversal, the end node of the first layer is head. In the second layer, the end node of the next layer recorded in the first layer will be used as the end node of the current layer. The next end node will be updated while going out and in, and the number of nodes in each layer will be recorded at the same time.
public static int levelMax(Node head){
if (head == null){
return 0;
}
Queue<Node> queue = new LinkedList<Node>();
Node levelEnd = head; //End node of this layer
Node levelNextEnd = null; //Next end node
int levelNum = 0; //Number of nodes in this layer
int nodeMax = 0; //Maximum number of nodes
Node p = head;
queue.add(p);
while (!queue.isEmpty()){
p = queue.poll();
if (p.left != null){
//Update levelNextEnd at any time
levelNextEnd = p.left;
queue.add(p.left);
levelNum++;
}
if (p.right != null){
levelNextEnd =p.right;
queue.add(p.right);
levelNum++;
}
if (p == levelEnd){
//Traverse to the last node of the layer and update the data
levelEnd = levelNextEnd;
nodeMax = Math.max(levelNum, nodeMax);
levelNum = 0;
levelNextEnd = null;
}
}
return nodeMax;
}
Topic 2: judgment of related concepts of binary tree
1. How to determine whether it is a search binary tree (sort binary tree)
Idea: the sequence obtained by traversing the binary tree in medium order. If it is an ascending sequence, it is a search binary tree
Recursive middle order:
public static void inOrderRecur(Node head){
if (head == null){
return;
}
inOrderRecur(head.left);
System.out.println(head.value + " ");
inOrderRecur(head.right);
}
Code modification:
public static int preValue = Integer.MIN_VALUE;
public static boolean checkBST(Node head){
if (head == null){
return true;
}
if (!checkBST(head.left)){
//Recursive left subtree
return false;
}
if (head.value <= preValue){
//Right < = left, not meeting BST
return false;
}else {
preValue = head.value;
}
return checkBST(head.right);
}
Non recursive middle order:
public static void inOrderRecur(Node head){
if (head != null){
Stack<Node> stack = new Stack<Node>();
Node p = head;
while (!stack.isEmpty() || p != null){
if (p != null){
stack.push(p);
p = p.left;
}else {
p = stack.pop();
System.out.println(p.value + " ");
p = p.right;
}
}
}
}
Code modification:
public static boolean checkBST(Node head){
if (head != null){
Stack<Node> stack = new Stack<Node>();
Node p = head;
int preValue = Integer.MIN_VALUE;
while (!stack.isEmpty() || p != null){
if (p != null){
stack.push(p);
p = p.left;
}else {
p = stack.pop();
if (p.value <= preValue){
return false;
}else {
preValue = p.value;
}
p = p.right;
}
}
}
return true;
}
Summary: both are dynamic checks. You can also store the sequence of binary tree into the set of list class to judge whether the sequence is orderly
2. How to judge whether it is a complete binary tree
Idea: breadth first (level traversal), judgment 1: return false as long as there is a node with a right child and no left child; Judgment 2: start from the incomplete node of the first subtree, and the subsequent nodes must be leaf nodes
public static boolean isCBT(Node head){
if (head == null){
return true;
}
Queue<Node> queue = new LinkedList<Node>();
boolean flag = false; //Indicates whether a node with incomplete subtree is encountered
Node p = head;
queue.add(p);
while (!queue.isEmpty()){
p = queue.poll();
if ((p.left == null && p.right != null) || flag && (p.left != null && p.right != null)){
//Condition of not full binary tree
return false;
}
if (p.left != null){
queue.add(p.left);
}
if (p.right != null){
queue.add(p.right);
}
if (p.left == null || p.right == null){
//Subtree incomplete
flag = true;
}
}
return true;
}
3. How to judge whether it is a full binary tree
Idea: count the depth l of the binary tree, and the number of nodes is N. if N = 2 ^ L - 1, it is a full binary tree
Methods: call recursively to find L and N of the left subtree; Find L, n of right subtree; Find the L, n of the tree
public static boolean isFull(Node head){
ReturnType returnType = process(head);
//1 < < x, x power of 2
return returnType.num == (1 << returnType.height - 1);
}
public static class ReturnType{
//Custom type
public int height; //Tree height
public int num; //Number of nodes
public ReturnType(int height, int num){
//Constructor
this.height = height;
this.num = num;
}
}
public static ReturnType process(Node head){
if (head == null){
return new ReturnType(0, 0);
}
ReturnType leftTree = process(head.left); //Recursive call
ReturnType rightTree= process(head.right);
int height = Math.max(leftTree.height, rightTree.height) + 1; //height
int num = leftTree.num + rightTree.num + 1; //Number of nodes
return new ReturnType(height, num);
}
4. How to judge whether it is a balanced binary tree
Idea: balanced binary tree conditions: (1) left subtree balance, left height; (2) Right subtree balance, right height; (3) | left height - right height | < = 1
Combined with recursive implementation
public static boolean isBalancedTree(Node head){
return process(head).isBalanced;
}
public static class ReturnType{
//Custom type
public boolean isBalanced; //Is the tree balanced
public int height; //Tree height
public ReturnType(boolean isBalanced,int height){
//Constructor
this.isBalanced = isBalanced;
this.height = height;
}
}
public static ReturnType process(Node head){
if (head == null){
//Empty tree balance, height 0
return new ReturnType(true, 0);
}
ReturnType leftTree = process(head.left); //Recursive call
ReturnType rightTree= process(head.right);
int height = Math.max(leftTree.height, rightTree.height) + 1;
boolean isBalanced = leftTree.isBalanced && rightTree.isBalanced
&& Math.abs(leftTree.height - rightTree.height) < 2;
return new ReturnType(isBalanced, height);
}
5. Binary tree recursive routine (tree DP, dynamic programming)
Idea: when judging what kind of binary tree is? Decomposed into whether the left subtree is satisfied, whether the right subtree is satisfied, and whether the left and right subtrees are satisfied after merging (tree type DP)
- Binary tree recursive routine: judge whether it is a search binary tree
(1) Left tree search, left max, min; (2) Right tree search, min, max; (3) Left Max < head Value < right min
public static boolean isBSTree(Node head){
return process(head).isBST;
}
public static class ReturnType{
//Custom type
public boolean isBST; //Is the tree a search tree
public int min; //Minimum value of tree
public int max; //Maximum value of the tree
public ReturnType(boolean isBST,int min, int max){
//Constructor
this.isBST = isBST;
this.min = min;
this.max = max;
}
}
public static ReturnType process(Node head){
if (head == null){
//The min and max of the empty tree are not easy to set, so they are directly set to null
return null;
}
ReturnType leftTree = process(head.left); //Recursive call
ReturnType rightTree= process(head.right);
int min = head.value; //Setting of min and max
int max = head.value;
if (leftTree != null){
min = Math.min(min, leftTree.min);
max = Math.max(max, leftTree.max);
}
if (rightTree != null){
min = Math.min(min, rightTree.min);
max = Math.max(max, rightTree.max);
}
boolean isBST = true; //isBST settings
if (leftTree != null && (leftTree.isBST || leftTree.max > head.value)){
//If the left is not empty: the left subtree is not a search binary tree or the left Max > head, value
//Does not satisfy the search Binary Tree
isBST = false;
}
if (rightTree != null && (rightTree.isBST || rightTree.min < head.value)){
isBST = false;
}
return new ReturnType(isBST, min, max);
}
- This method is used to judge full binary tree and balanced binary tree
Topic 3: the lowest common ancestor of two nodes
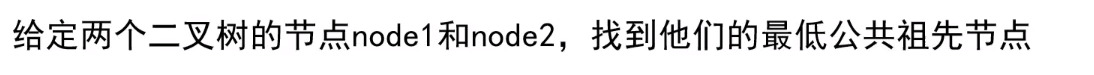
- Written examination ideas:
(1) Use HashMap to establish the relationship between each node and its parent node
(2) Use HashSet to store all the ancestor nodes of node1
(3) Find the ancestor node of node2 in turn, and find whether there are the same in the HashSet of node1. When the first one is the same, it is the lowest common ancestor node
public static Node lowCommonAncestor(Node head, Node node1, Node node2){
HashMap<Node, Node> fatherMap = new HashMap<Node,Node>();
fatherMap.put(head, head); //The parent node of the head node is itself
process(head, fatherMap);
HashSet<Node> setNode1 = new HashSet<Node>(); //Establish the ancestor node set of node1
Node p = node1;
while (p != fatherMap.get(head)){
//Traverse the header node from the current node node1 point from bottom to top
setNode1.add(p);
p = fatherMap.get(p);
}
p = node2;
while (p != fatherMap.get(head)){
//Traverse the header node from the current node2 node from bottom to top
if (setNode1.contains(p)){
//Having the same is the lowest common ancestor node
return p;
}
p = fatherMap.get(p);
}
return null;
}
public static void process(Node head, HashMap<Node, Node> fatherMap){
//Establishment of relationship between node and parent node
if (head == null){
return;
}
fatherMap.put(head.left, head);
fatherMap.put(head.right, head);
process(head.left, fatherMap);
process(head.right, fatherMap);
}
- Interview ideas:
Situation analysis:
(1) Node1 is the ancestor node of node2, or node2 is the ancestor node of node1
(2) node1 and node2 are not ancestral nodes to each other. They need to traverse upward to find them
Method: traverse the tree node, encounter node1, node2 returns the corresponding node, and the other nodes just return null
Case 1:
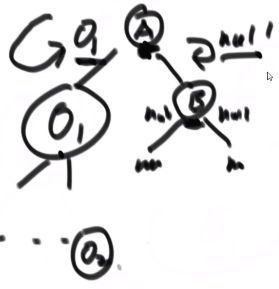
Case 2:

public static Node lowCommonAncestor(Node head, Node node1, Node node2){
if (head == null || head == node1 || head == node2){
//Returns the corresponding value when node1 and node2 are selected
return head;
}
Node left = lowCommonAncestor(head.left, node1, node2);
Node right = lowCommonAncestor(head.right, node1, node2);
if (left != null && right != null){
//In case 2, the two nodes are not common ancestors to each other
//At the same time, it returns to node1 on the left and right, and node2 is the lowest common ancestor
return head;
}
//When one of node1 and node2 is encountered, it returns a non empty value
return left != null ? left : right;
}
Topic 4: subsequent node search of tree (including parent node)

Successor node: in the middle order traversal sequence, the next node of node is called the successor node of node
Situation analysis:
(1) If a node has a right subtree, the successor node is the leftmost node of the right subtree
(2) If the node has no right subtree, the subsequent node is the rightmost node of the left subtree of that node (judge whether the current node is the left subtree of its ancestor node)
public static Node getSuccessorNode(Node node){
if (node == null){
return node;
}
if (node.right != null){
//The current node has a right subtree
return getLeftNode(node);
}
else {
//No right subtree, find through parent node
Node parent = node.parent;
while (parent != null && parent.left != node){
//Is this node the left subtree of the parent node
node = parent;
parent = node.parent;
}
return parent;
}
}
public static Node getLeftNode(Node node){
if (node == null){
return node;
}
while (node.left != null){
node = node.left;
}
return node;
}
Topic 5: serialization and deserialization of binary tree

Idea: use "#" to represent the representation between separated nodes; use "#" to represent empty nodes
Preorder sequence: serialization
public static String serialByPre(Node head){
if (head == null){
return "#_";
}
String str = head.value + "_";
str += serialByPre(head.left);
str += serialByPre(head.right);
return str;
}
Deserialization
public static Node reconByPreString(String preStr){
//Split the string and store it in the queue
String[] values = preStr.split("_");
Queue<String> queue = new LinkedList<String>();
for (int i = 0; i < values.length; i++){
queue.add(values[i]);
}
return reconPreOrder(queue);
}
public static Node reconPreOrder(Queue<String> queue){
//Restore tree through queue
String value = queue.poll();
if (value.equals("#")){
return null;
}
Node head = new Node(Integer.valueOf(value));
head.left = reconPreOrder(queue);
head.right = reconPreOrder(queue);
return head;
}
Topic 6: origami problem

Problem analysis:

Idea: find the law of origami and use the way of tree to express it. Both the parent node and the left subtree are concave, and the right subtree is convex
Methods: given N, determine the height of the tree, and simulate the middle order traversal of the tree to get the crease direction
public static void printAllFolds(int N){
printProcess(1, N, true);
}
public static void printProcess(int height, int N, Boolean down){
//Middle order traversal of simulated tree
//Height current height, N is the tree height
//Down = true - > concave, down = false - > convex
if (height > N){
return;
}
printProcess(height + 1, N, true);
System.out.println(down ? "concave" : "Convex");
printProcess(height + 1, N, false);
}