Problem description

• Problems solved by Manacher algorithm:
  (1) How to solve the length of the longest palindrome substring in string str
  (2) How to achieve time complexity O(N)?

Conventional thinking

• Traverse each character, regard each character as a center (axis of symmetry), and expand to the left and right respectively. The same will continue to expand, and the different will end
• Disadvantages: palindromes with an even number of characters, whose center (axis of symmetry) is not a single character, will be ignored
• Solution skills: when processing characters with length of n, add special characters between the gaps of the original characters. At this time, palindromes with even characters can be converted into odd ones to solve
• Example:
  (1) Original character: 1 2 2 1 3 1 2 2 1 if 1 2 2 1 is counted, it will be ignored
  (2) Add special characters: # 1 # 2 # 2 # 2 # 1 # 3 # 1 # 2 # 2 # 1 #. At this time, the number of palindromes is odd and can be counted
• The longest palindrome is counted. Because special characters are added, the result is divided by 2 and rounded down, which is the answer
• Selection of special characters: special characters can be arbitrary, even if they have appeared in the original characters. In fact, each comparison is between the original characters and newly filled characters, so the selection of special characters does not affect the record
• Time complexity O(N ^ 2), N is the number of characters

Manacher thought

• Similar to kmp, Manacher accelerates on the basis of conventional ideas
• It is improved on the basis of adding special characters in the conventional idea
• Basic concepts:
  (1) Palindrome radius and palindrome diameter: size of expansion area
  (2) Palindrome radius array: records the palindrome radius of each character
  (3) Palindrome right boundary: int type, with the initial value of - 1. It is the last position of the rightmost boundary that can be reached in the process of right expansion
  (4) Palindrome center point: int type, with an initial value of - 1. When the rightmost boundary is reached in the process of right expansion, the subscript of the center point
  (5) The right boundary of palindrome is used together with the center point and updated at the same time
• Situation analysis:
  (1) The current point i is not in the right boundary of palindrome: violent expansion, no optimization, direct expansion
  (2) The current point i is in the right boundary of palindrome: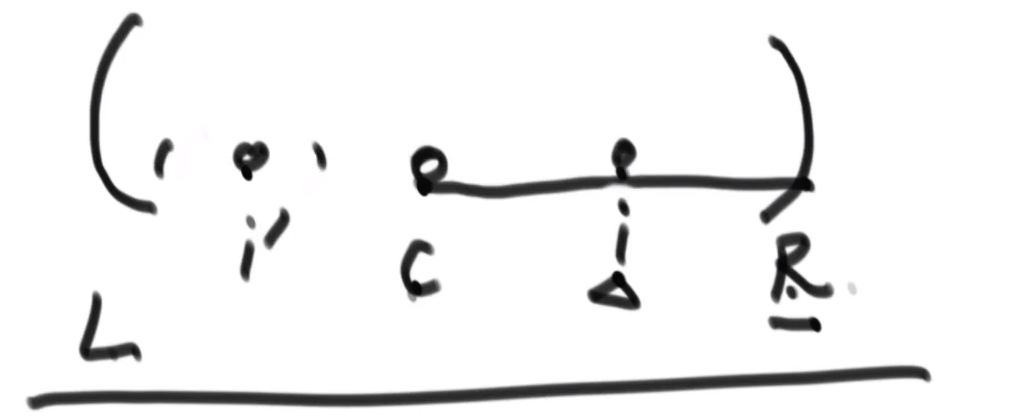
  50: L eft boundary, R: right boundary, C: center point, i ': i symmetry point about C
  The palindrome of i 'can be obtained in the palindrome radius array
  (a) if the palindrome area of i 'is inside L, the palindrome radius of i is the palindrome radius of i'
  (b) if a part of the palindrome area of i 'is already outside L, the palindrome radius of i is the part from i to R
  (c) the palindrome area of i 'coincides with L, and the palindrome radius of i must be > = the part from i to R. it is necessary to compare the thing after r with the symmetry point R' of R about i to judge the palindrome area
• Time complexity O(N), N is the number of characters

code implementation

• If the results of usage analysis are judged one by one, the implementation code is too cumbersome
• You can integrate the parts that do not need to judge the palindrome. After obtaining the corresponding palindrome radius, skip the parts that do not need to be judged, and judge whether the rest of the code can be expanded
  (1) In case 1, the part that does not need to be compared is that the palindrome radius starts from 1
  (2) In case 2, a is the minimum value, and both b and c are based on the palindrome right boundary - i, then compare the size of prearr [i '] and R - i + 1, and the smaller value is the part without judgment

    public static int manacher(String str){
        if (str == null || str.length() == 0){
            return 0;
        }
        char[] chs = manacherString(str); //Add special characters
        int[] preArr = new int[chs.length]; //Palindrome radius array
        int mid = -1; //Palindrome Center
        int R = -1; //Palindrome right boundary
        int max = Integer.MIN_VALUE; //Maximum palindrome length
        for (int i = 0; i < chs.length; i++){
            //Traversal character array
            //Area without judgment
            //i < = r the current point i is not at the right boundary, and the palindrome radius is at least 1
            //There are two cases where i is on the right boundary: the palindrome of i 'is inside L or outside L
            //Through the minimum value of symmetry point i 'or R - i, we can judge which case is
            preArr[i] = R > i ? Math.min(preArr[2 * mid - i], R - i + 1) : 1;
            while (i + preArr[i] < chs.length && i - preArr[i] > -1) {
                //Without exceeding the left and right character arrays
                //In either case, judge whether it can be expanded to simplify the code
                if (chs[i + preArr[i]] == chs[i - preArr[i]]){
                    //Satisfy extension
                    preArr[i]++;
                }else {
                    break;
                }
            }
            if (i + preArr[i] > R){
            	//Update R, mid
                R = i + preArr[i] - 1;
                mid = i;
            }
            max = Math.max(max, preArr[i]);
        }
        //The original string is an extended string, and the palindrome radius is - 1
        return max - 1;
    }

    public static char[] manacherString(String str) {
        //Add special characters so that the length of palindrome characters becomes even
        char[] strArr = str.toCharArray();
        char[] chs = new char[str.length() * 2 + 1];
        for (int i = 0, j = 0; i < chs.length; i++){
            //Add special characters to even positions
            chs[i] = (i & 1) == 0 ? '#' : strArr[j++];
        }
        return chs;
    }