Finally, the last question, because this question has really been tried many times and can't pass the test, so I'll write the later one first and come back to fill in this question. ok, the following is the only two difficult questions in this preliminary contest, which is also the last one, similar string group

T18 if two letters at different positions in string X are exchanged so that it is equal to string Y, then x and Y are said to be similar. If the two strings themselves are equal, they are also similar.
For example, "tars" and "rates" are similar (exchange the positions of 0 and 2); "Rates" and "arts" are also similar, but "star" is not similar to "stars", "rates", or "arts".
In short, they form two association groups through similarity: {tars "," rats "," arts "} and {star"}. Note that "tars" and "arts" are in the same group, even if they are not similar. Formally, for each group, to determine a word in the group, it only needs to be similar to at least one word in the group.
Give you a list of strings strs. Each string in the list is an alphabetic word for all other strings in strs. How many similar string groups are there in strs?

Problem solving ideas:
At the beginning, in fact, I kept pushing it step by step through logical relations. Later, I found that I had torn down the east wall to make up the west wall, and I didn't fix the bug. After reading the problem solution, I knew that there was such a thing and collected it. Next, I'll talk about my understanding.
In fact, similar string groups are similar to the maximum number of saves made before. If each number is regarded as a point, the similarity between the two points means that the two points are connected and form a group. We need to find the maximum number of groups.
The essence of joint query set is to establish a list containing all points. The index of the list represents the point, and the value represents the previous connection of the point. For ease of understanding, let's take an example here. Combined with the code, it should be easier to understand
Suppose there are three points: 0, 1 and 2. 0 is connected with 1 and 2 respectively. The initial table d is [0, 1 and 2], representing 0 connected with 0, 1 connected with 1 and 2 connected with 2. Traversal: first, it is found that 0 is connected with 1, then the initial table d becomes [1, 1, 2], indicating that 0 is connected with 1, 1 is connected with 1, 2 is connected with 2; Then, it is found that 0 is connected with 2, and d is updated to [1, 2, 2], indicating that 0 is connected with 1, 1 is connected with 2, 2 is connected with 2; Here, 2 represents the highest level. The next level is 1, and then the next level is 0. After all traversals are completed, those that remain the original value are all the highest levels. The number is the number of all groups. The code is as follows:

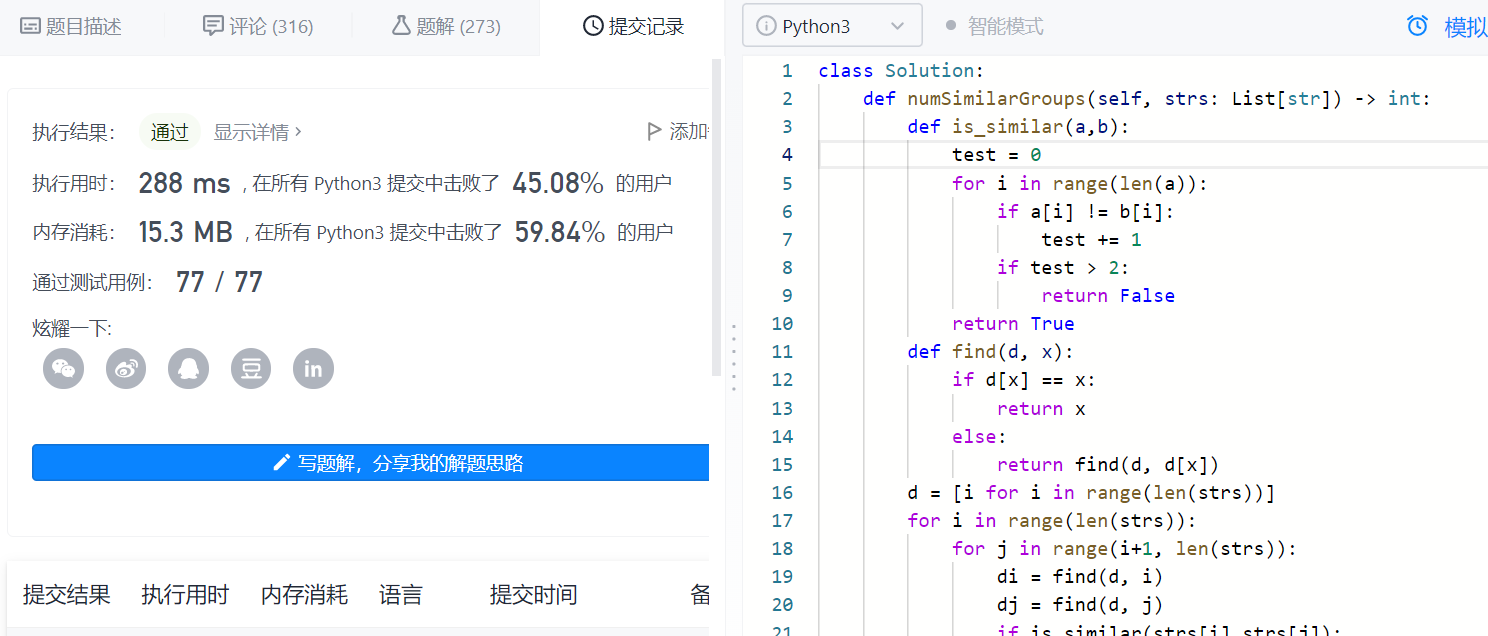
class Solution:
    def numSimilarGroups(self, strs: List[str]) -> int:
        def is_similar(a,b):
            test = 0
            for i in range(len(a)):
                if a[i] != b[i]:
                    test += 1
                if test > 2:
                    return False    
            return True
        def find(d, x):
            if d[x] == x:
                return x
            else:
                return find(d, d[x])
        d = [i for i in range(len(strs))]
        for i in range(len(strs)):
            for j in range(i+1, len(strs)):
                di = find(d, i)
                dj = find(d, j)
                if is_similar(strs[i],strs[j]):
                    d[di] = dj
        res = 0
        for i in range(len(strs)):
            if d[i] == i:
                res += 1
        return res

Operation results:

Then attach the method of pushing the logic you think a little. yysy has a bug, so I won't talk more here. Write it down. It's right to represent my futile morning. You can use the one above

class Solution:
    def numSimilarGroups(self, strs: List[str]) -> int:
        
        def is_similar(a,b):
            test = 0
            for i in range(len(a)):
                if a[i] != b[i]:
                    test += 1
            if test == 2 or test == 0:
                return True
            else:
                return False
        used = [False]*len(strs)
        test = [[] for _ in range(len(strs))]
        res = 0
        f = 0
        for i in range(len(strs)):
            for j in range(i+1,len(strs)):
                for t in test:
                    if i in t and j in t:
                        f = 1
                        break
                if f == 1:
                    f = 0
                    continue
                if is_similar(strs[i], strs[j]):
                    if used[i] and used[j]:
                        res -= 1
                    if not used[i] and not used[j]:
                        res += 1
                    used[i] = True
                    used[j] = True
                    test[i].append(j)
        for i in used:
            if not i:
                res += 1
        if res < 0 :
            return 1
        return res