The title comes from: https://leetcode-cn.com/study-plan/dynamic-programming/?progress=nc4eyhc

Climbing stairs (simple)

class Solution {
    public int climbStairs(int n) {
        if (n <= 2 ) {
            return n;
        }
        int[] ans = new int[n + 1];
        ans[1] = 1;
        ans[2] = 2;
        for (int i = 3; i <= n; i++) {
            ans[i] = ans[i - 1] + ans[i - 2];
        }
        return ans[n];
    }
}

Climbing stairs with minimum cost (simple) (advanced version of climbing stairs)

Note that the last element of cost is not the roof. You need to climb once to reach the roof. You also need to pay attention to the state transition equation and base case.

State transition equation:
d p [ n ] = m i n ( d p [ n − 1 ] + c o s t [ n − 1 ] , d p [ n − 2 ] + c o s t [ n − 2 ] ) dp[n] = min(dp[n-1] + cost[n-1], dp[n-2] + cost[n-2]) dp[n]=min(dp[n−1]+cost[n−1],dp[n−2]+cost[n−2])
Initial situation: because the title says it can start from the steps of 0 and 1 subscripts, their cost = 0.

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // min(dp[n-1]+cost[n-1], dp[n-2]+cost[n-2])
        int n = cost.length;
        int[] dp = new int[n + 1];
        // base case
        dp[0] = 0;
        dp[1] = 0;
        // Iterate all States
        for (int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[n];
    }
}

House raiding (medium)

Think about such a question. What is the state of a certain room? It's very simple to grab and not grab, so you can write the state transition equation:
d p [ n ] = m a x ( d p [ n − 1 ] , d p [ n − 2 ] + n u m s [ n ] ) dp[n] = max(dp[n-1], dp[n-2] + nums[n]) dp[n]=max(dp[n−1],dp[n−2]+nums[n])
Choose not to rob, then the next one can rob; If you choose to rob, you can't rob the next one. Compare the value of robbing and not robbing, and you can get the final answer.

In the initial situation, room 1 is its own value (because it is a house that has the greatest value only if it is robbed). For room 2, it is necessary to judge whether to rob room 1 or room 2, and choose a room with greater value.

Note that the subscript of room 1 in the title is 0.

class Solution {
    public int rob(int[] nums) {
        // There are two states for each house: rob (plus the value of this house) and don't rob (it depends on the value of the next house)
        // dp[n] = max(dp[n-1], dp[n-2] + nums[n])
        // Note that the subscript 0 in the title records the value of room 1
        int n = nums.length;
        if (n == 1) {
            return nums[0];
        }
        if (n == 2) {
            return Math.max(nums[0], nums[1]);
        }
        int[] dp = new int[n + 1];
        // base case
        // Room number starts from 1
        dp[1] = nums[0];
        // Room 2 is divided into: Rob room 1 and not rob room 1
        dp[2] = Math.max(nums[0], nums[1]);
        // Traverse all States
        for (int i = 3; i <= n; i++) {
            // nums[i - 1] is because nums room 1 starts with subscript 0
            dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
        }
        return dp[n];
    }
}

Home robbing II (medium)

Different from the previous question, room 1 and the last room are connected together. Think about what problems this will lead to?
The connection shows that once room 1 is robbed, the last room cannot be robbed; Room 1 was not robbed, and the last room may be robbed (note that it is only possible, because the last room can be robbed or not). Room 1 in the previous question has only one state, but room 1 in this question has two states. The state of the next room 1 must be determined before the state of the subsequent rooms can be determined.

Therefore, we can divide the state of room 1 into two cases: grab No. 1 and not grab No. 1, because the initialization of dp array is different in the two cases. Finally, compare the total robbery money in the two states, and take the largest.

Grab No. 1: then the subsequent steps are the same as the previous question, but in the end, pay attention to room n, dp[n] can only be equal to dp[n-1], because room n can't be robbed!!!

No. 1: dp[1]=0, dp[2]=nums[2-1], and then iterate with the same state transition equation. Note that room n can be robbed or not.

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return nums[0];
        }
        if (n == 2) {
            return Math.max(nums[0], nums[1]);
        }
        int[] dp = new int[n+1];
        // If it is connected, then room 1 may be robbed or not. We need to compare the value of the two cases
        // Look at room 1 first
        dp[1] = nums[0];
        // Room 2, see if it's number 1 or number 2
        dp[2] = Math.max(nums[0], nums[1]); 
        for (int i = 3; i < n; i++) {
            // It is divided into robbery and non robbery
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
        }
        // Note that because room 1 is robbed, room n cannot be robbed!!
        // At this time, the value of room n can only be dp[n-1]
        int first = dp[n-1];
        // Look at room 1 again. Don't rob it
        dp = new int[n+1];
        dp[1] = 0;
        dp[2] = nums[1];
        // Although room 1 is not robbed, room n may also be robbed or not robbed
        // It must be noted that if room 1 is not robbed, it does not mean that room n will be robbed
        for (int i = 3; i <= n; i++) {
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
        }
        return Math.max(first, dp[n]);
    }
}

In order to facilitate understanding, dp array is used when writing code, but it can be represented by several pointers, which can optimize space consumption.

Delete and gain points (medium)

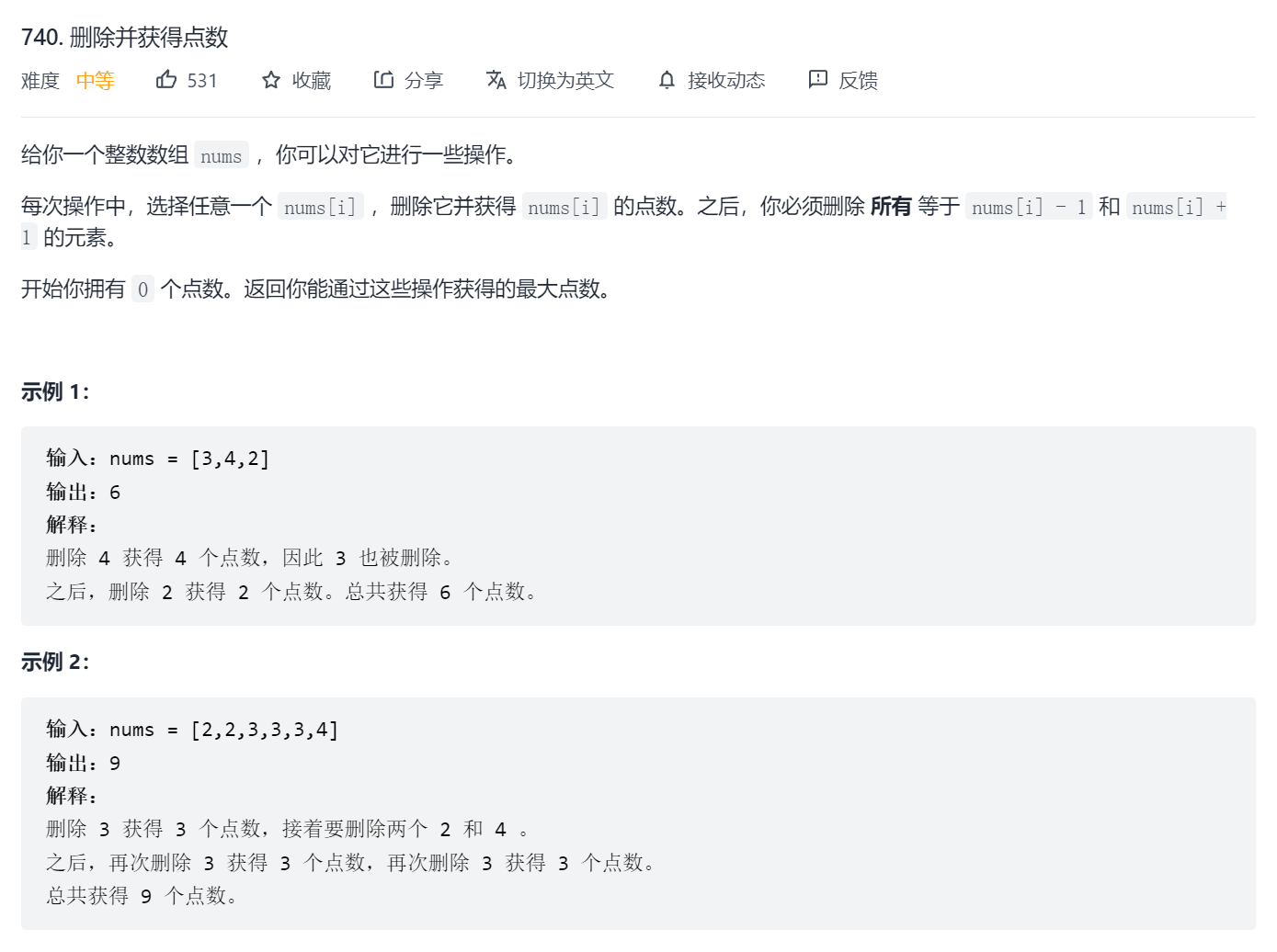
Discuss a number. It has two states: delete and not delete. If it is deleted, directly obtain its corresponding points (hidden here. In fact, the obtained points = the corresponding points * the number of the number, because you delete a number, the same number may still exist in the array. Deleting them will obtain the same points and will not have a new impact on the array), Therefore, the state transition equation can be obtained. For a positive integer n:
d p [ n ] = m a x ( d p [ n − 2 ] + c n t [ n ] ∗ n , d p [ n − 1 ] ) dp[n] = max(dp[n-2]+cnt[n] * n, dp[n-1]) dp[n]=max(dp[n−2]+cnt[n]∗n,dp[n−1])

base case: how to set the initial state of this question? What does dp[n] array mean?
It should be: "dp[i] means that the maximum number of points obtained by deleting element I (Num [i]) in array num is dp[i]. Note that the range of array elements you operate on at this time is [0, i].".
In fact, we default to find the maximum number of points from 0, so dp[0] = 0, dp[1] = 1 * cnt[1], dp[2] = max(dp[0] + 2 * cnt[2], dp[1])

Many times, it's easy to get the state transition equation when you do more questions, but you don't know what dp array means. In this way, although you can do questions, you don't give a good impression to the interviewer!

class Solution {
    public int deleteAndEarn(int[] nums) {
        // There are two situations for number n: delete and not delete (once deleted, you can get as many points as there are)
        // It must be noted that after deleting that number, the number of points obtained is: that number * number
        // DP [n] = max (DP [n-2] + CNT [n] * number of N numbers, dp[n-1])
        int n = nums.length;
        if (n == 1) {
            return nums[0];
        }
        if (n == 2) {
            if (nums[1] == nums[0] + 1 || nums[1] == nums[0] - 1) {
                return Math.max(nums[0], nums[1]);
            } else if (nums[0] == nums[1]) {
                return 2 * nums[0];
            } else {
                return nums[0] + nums[1];
            }
        }
        int max = -1;
        // Find the maximum value to determine the size of the array
        for (int i = 0; i < n; i++) {
            if (nums[i] > max) {
                max = nums[i];
            }
        }
        int[] cnt = new int[max + 1];
        // Count each number in the array
        for (int i = 0; i < n; i++) {
            cnt[nums[i]]++;
        }
        int[] dp = new int[max + 1];
        // dp[i] represents the maximum value that can be formed within the integer range of 1 < = x < = I
        dp[1] = 1 * cnt[1];
        dp[2] = Math.max(dp[0] + 2 * cnt[2], dp[1]);
        for (int i = 3; i <= max; i++) {
            dp[i] = Math.max(dp[i - 2] + i * cnt[i], dp[i - 1]);
        }
        return dp[max];
    }
}

Jumping game (medium)

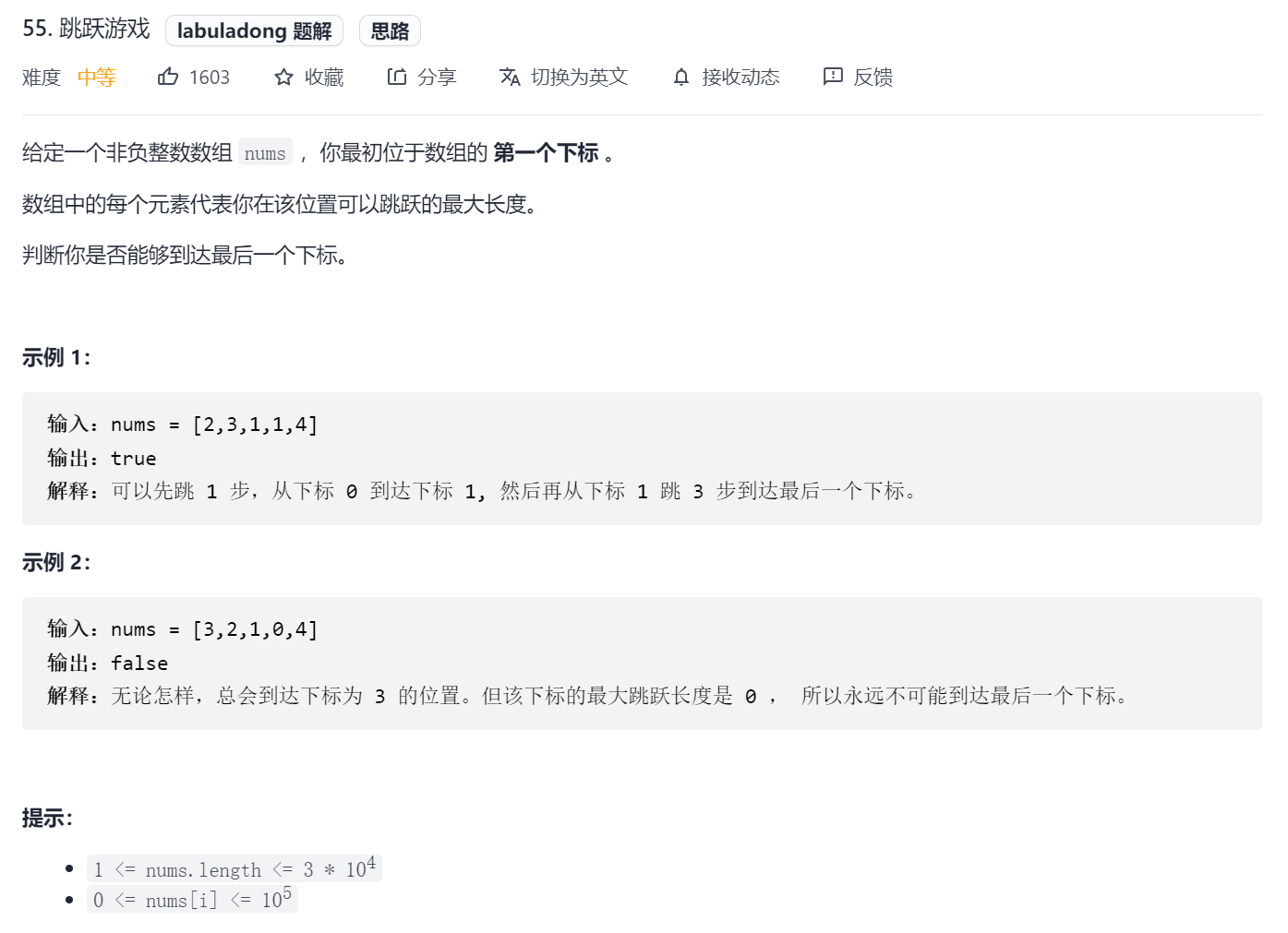
Initial perception, traverse each subscript and its elements, and mark the reachable position as true.

class Solution {
    public boolean canJump(int[] nums) {
        // Num [i] is the maximum length that can jump at this position, which means that you can jump or not
        // nums[0] = 2 dp[0] = true dp[1] = true dp[2] = true
        int n = nums.length;
        if (nums[0] >= n - 1) {
            return true;
        }
        boolean[] dp = new boolean[n];
        for (int i = 0; i <= nums[0]; i++) {
            dp[i] = true;
        }
        for (int i = 1; i < nums.length; i++) {
            if (dp[i] == true) {
                for (int j = 0; j <= nums[i]; j++) {
                    if ((i + j) < n) {
                        dp[i + j] = true;
                    } else {
                        break;
                    }
                }
            }
        }
        return dp[n - 1];
    }
}

Can it be optimized? Note that the element corresponding to each subscript refers to the maximum position that can jump, which means that you can jump 0-n steps. Then we can directly see how far the current subscript can jump, because positions smaller than the maximum subscript can jump.

class Solution {
    public boolean canJump(int[] nums) {
        // Num [i] is the maximum length that can jump at this position, which means that you can jump or not
        // Key point: if k can be reached farthest from the current position, all positions before k can be reached
        int n = nums.length;
        int dp = 0;
        for (int i = 0; i < n; i++) {
            if (dp < i) {
                // The i subscript cannot be reached in the case of the previous maximum value
                return false;
            }
            // Only update the farthest subscript that can jump to, because all subscripts less than the farthest subscript can jump to
            dp = Math.max(dp, i + nums[i]);
        }
        return dp >= (n - 1);
    }
}

As can be seen from the above code, in fact, the problem-solving idea is more greedy, and dynamic planning can also be solved, but the speed is slow.

Jumping game II (medium)

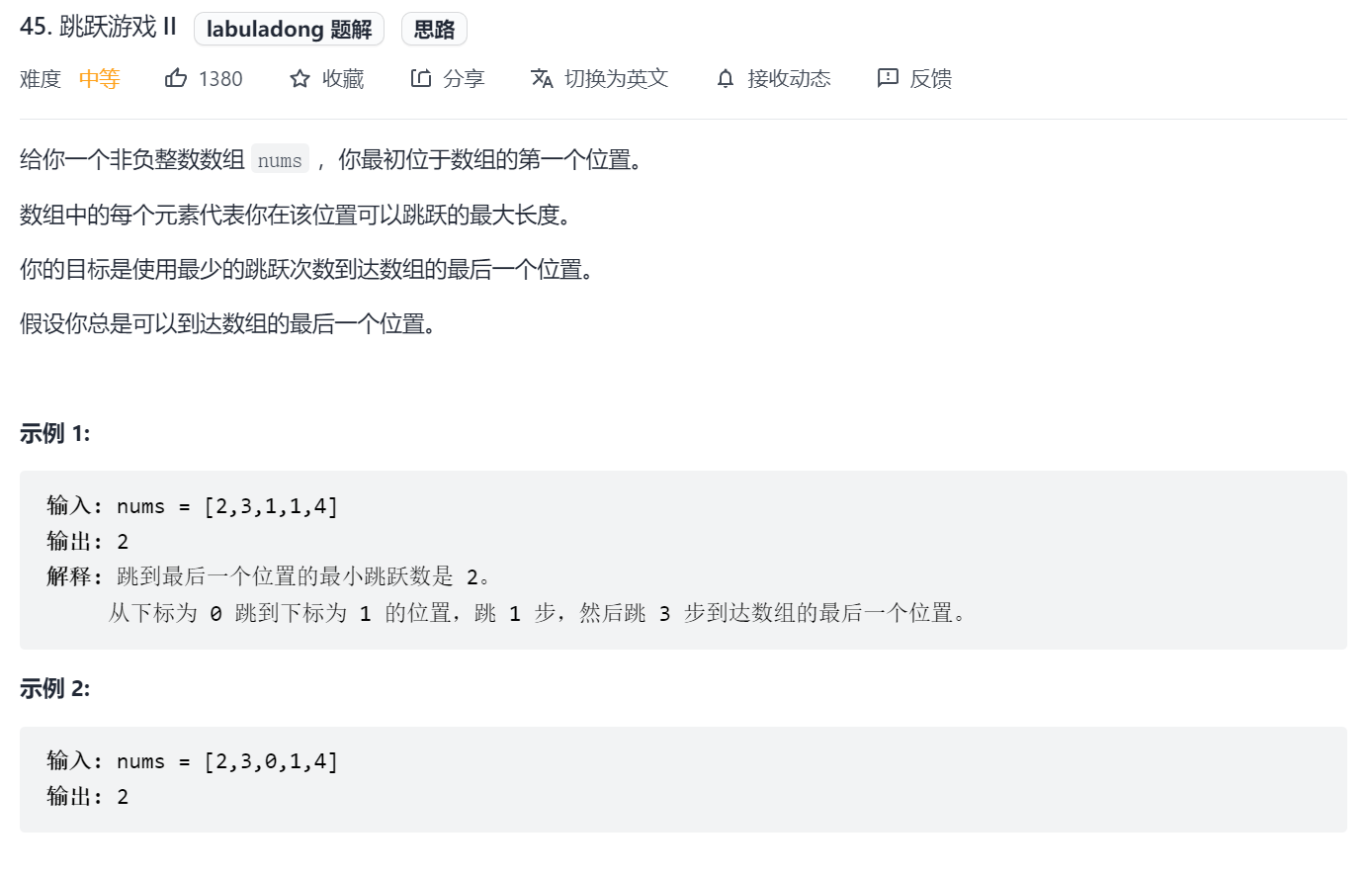
Traverse the subscripts that the current subscript can reach. If the number of hops is smaller, update the number of hops of the subscript. dp array records the minimum number of hops required to reach each subscript.

class Solution {
    public int jump(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return 0;
        }
        int[] dp = new int[n];
        Arrays.fill(dp, n);
        dp[0] = 0;
        for (int i = 0; i < n; i++) {
            // Record the farthest position that the current subscript can jump to
            int k = i + nums[i];
            int j = i + 1;
            while (j <= k && j < n) {
                dp[j] = Math.min(dp[j], dp[i] + 1);
                j++;
            }
        }
        return dp[n - 1];
    }
}

Maximum subarray sum (simple)

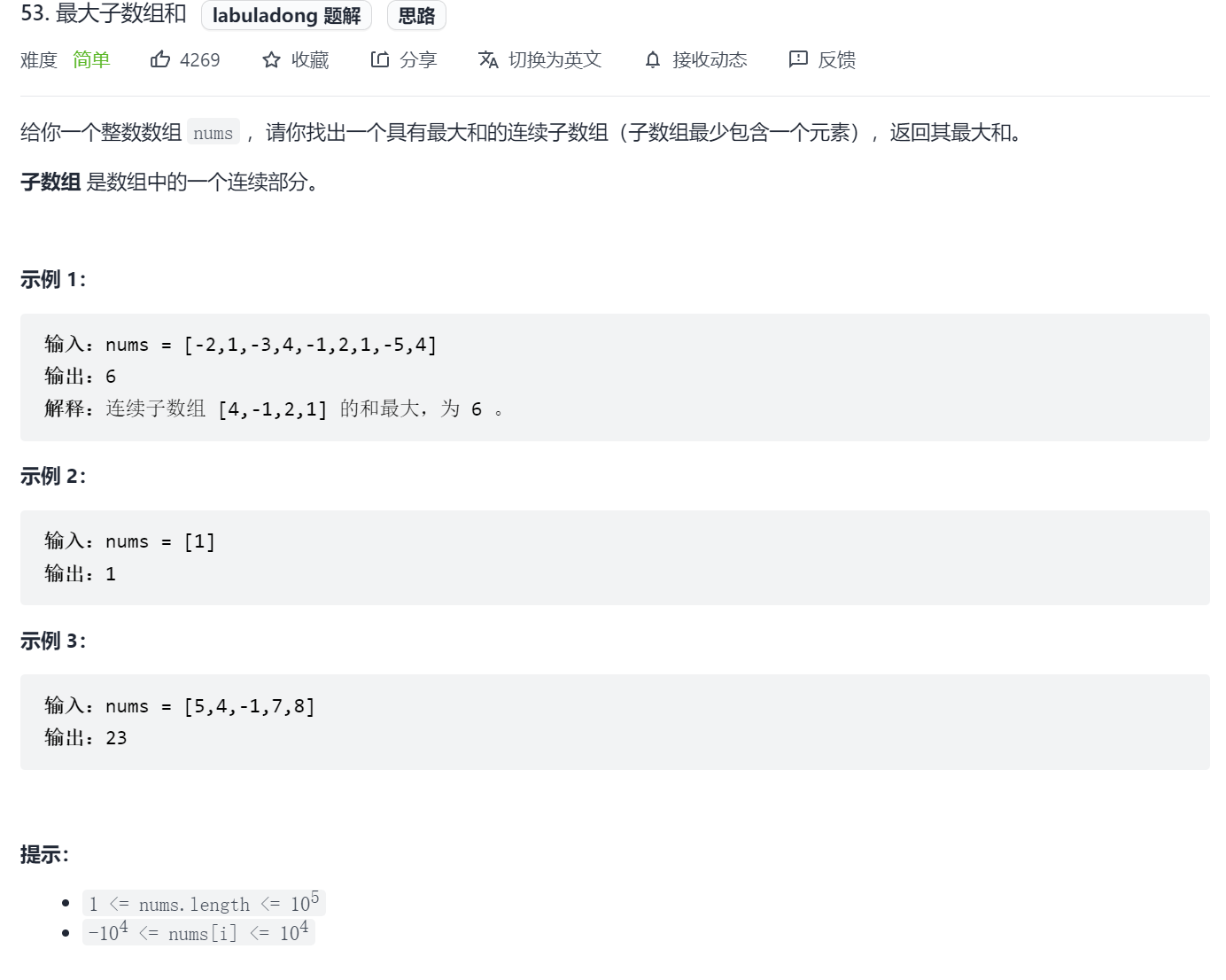
For a number in the array, there are two states: select it and deselect it. If you choose it, the global sum will be added to it. If you don't choose it, the global sum is itself, because the subarray must be continuous and have at least one number. The meaning of dp array is "the maximum sum of continuous subarrays" at the end of the ith number (under the condition of the title), so it's easy to write the state transition equation:
d p [ n ] = m a x ( d p [ n − 1 ] + n u m s [ n ] , n u m s [ n ] ) dp[n] = max(dp[n-1] + nums[n], nums[n]) dp[n]=max(dp[n−1]+nums[n],nums[n])
It can also be written as: if the previous dp is negative, it will be less than its own num, so just look at the previous dp value directly.
d p [ n ] = n u m s [ n ] + m a x ( d p [ n − 1 ] , 0 ) dp[n] = nums[n] + max(dp[n-1], 0) dp[n]=nums[n]+max(dp[n−1],0)
Note that because the meaning of dp array is the maximum sum of successive subarrays that must end with the ith number, dp[n] does not necessarily become the global maximum, and the recorded maximum should be compared at all times.

Write the corresponding code as follows:

class Solution {
    public int maxSubArray(int[] nums) {
        // For a number, there are two states: select it and deselect it
        // If it is not selected, the maximum sum of the first i numbers is itself (because it must contain at least one number)
        // If it is selected, the global and + current numbers
        int n = nums.length;
        int[] dp = new int[n + 1];
        // dp array represents the first i numbers of the array and the maximum sum that can be formed (Note: it is a continuous sub array and must contain a number)
        dp[0] = 0;
        int max = Integer.MIN_VALUE;
        // dp[n] = max(nums[n], dp[n-1] + nums[n])
        for (int i = 1; i <= n; i++) {
            dp[i] = Math.max(nums[i - 1], dp[i - 1] + nums[i - 1]);
            max = Math.max(dp[i], max);
        }
        return max;
    }
}

Extension: from the state transition equation of this problem, the state transition equation of the smallest array sum can be derived, as follows:
d p [ n ] = m i n ( d p [ n − 1 ] + n u m s [ n ] , n u m s [ n ] ) dp[n] = min(dp[n - 1] + nums[n], nums[n]) dp[n]=min(dp[n−1]+nums[n],nums[n])
It can also be written as:
d p [ n ] = n u m s [ n ] + m i n ( d p [ n − 1 ] , 0 ) dp[n] = nums[n] + min(dp[n - 1], 0) dp[n]=nums[n]+min(dp[n−1],0)

※ maximum sum of circular subarray (medium) (upgraded version of the previous question)

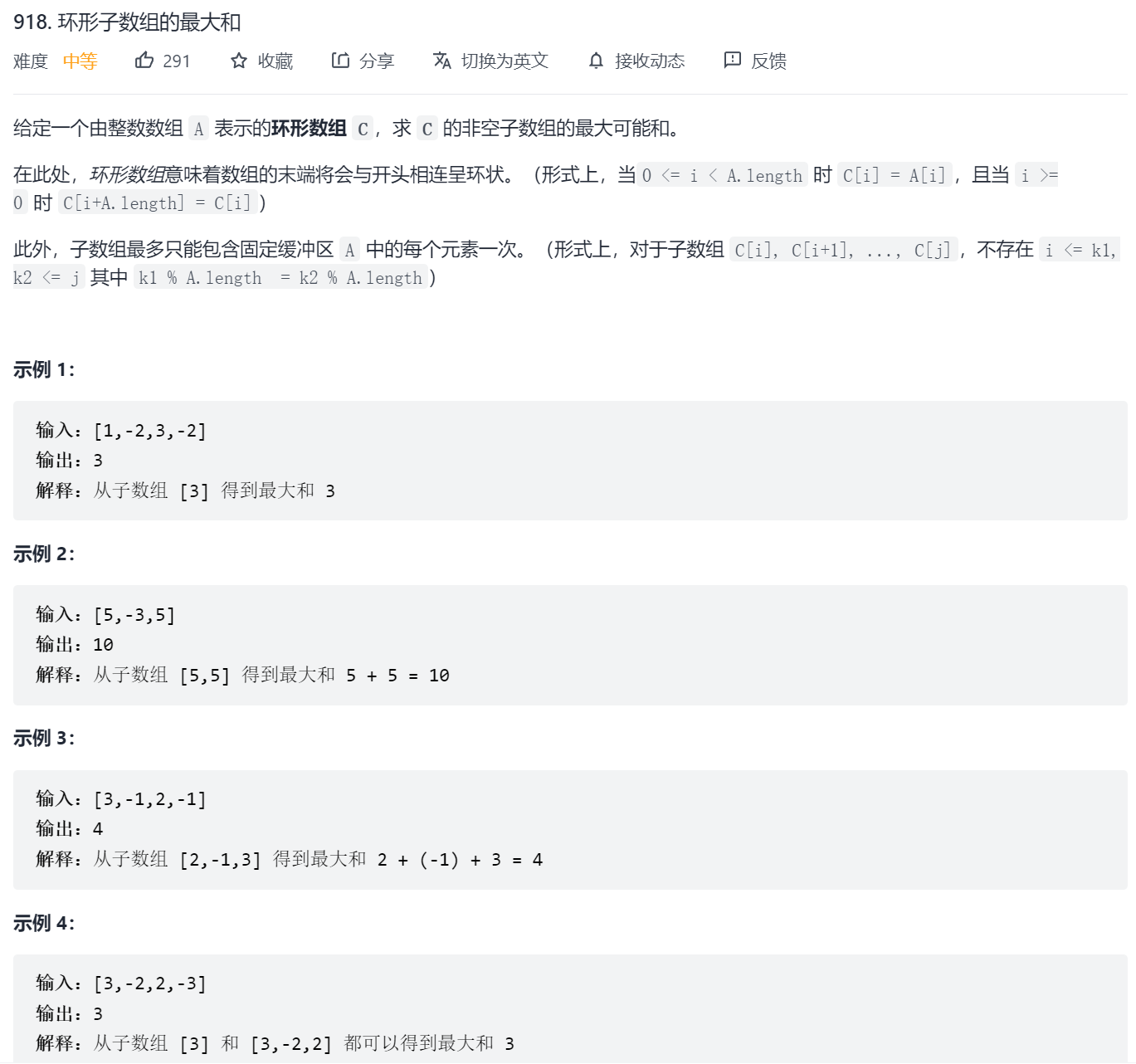
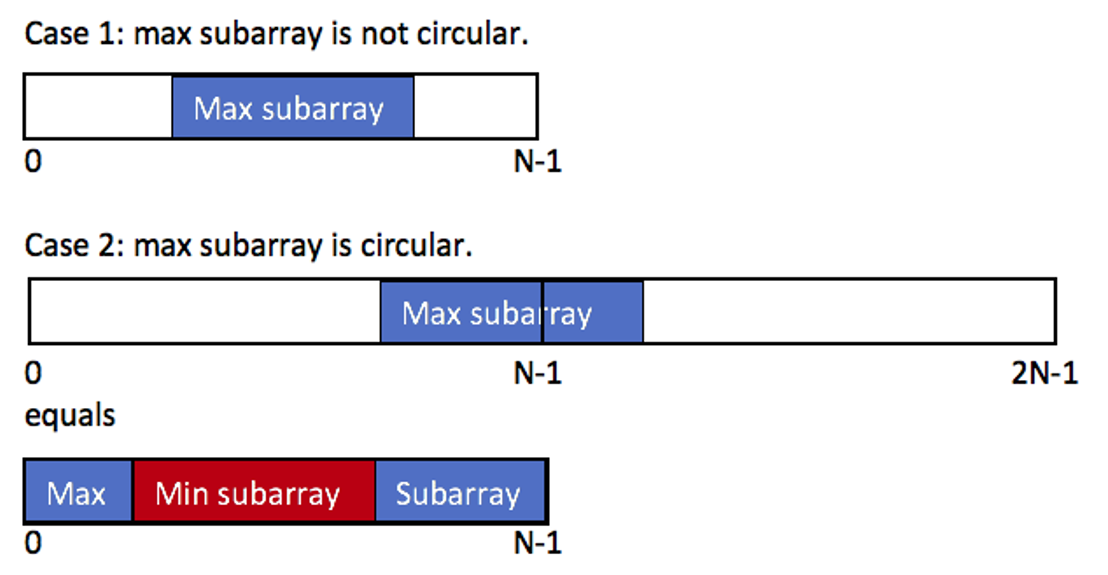
As shown in the figure above, the subarray that generates the maximum sum is only in two cases: one is not ring and the other is ring. The case of forming a ring is solved directly by the method of the previous question. How to solve the case of forming a ring?

A direct conclusion is given: the maximum value of the looped case = the sum of the arrays - the sum of the smallest arrays of the non looped parts

The certificate on LeetCode is posted here:
Address: https://leetcode-cn.com/problems/maximum-sum-circular-subarray/solution/wo-hua-yi-bian-jiu-kan-dong-de-ti-jie-ni-892u/

After obtaining the maximum value in the two cases, the larger one is obtained by comparison, which is the final answer.

This problem is similar to that of home robbing II. It should be discussed in two situations. In the future, we must discuss the problems of forming a ring separately.

class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        // There are two cases: the maximum sum is generated in the non looped state, and the maximum sum is generated in the looped state
        // If you don't form a ring first, you can solve it normally, just like problem 53
        int n = nums.length;
        if (n == 1) {
            return nums[0];
        }
        int[] dp = new int[n];
        dp[0] = nums[0];
        int max = nums[0];
        int sum = nums[0];
        for (int i = 1; i < n; i++) {
            // The second state transition equation is adopted
            dp[i] = nums[i] + Math.max(dp[i - 1], 0);
            max = Math.max(dp[i], max);
            // Count the sum of all elements in the array
            sum += nums[i];
        }
        // Then count the ring formation, and the subarray of the maximum sum must contain the first element and the last element (only in this way can the ring be formed)
        // Assumed array range: nums[0] - nums[n - 1]
        // Traversal range: num [1] - num [n - 2
        int min = nums[1];
        for (int i = 1; i < n - 1; i++) {
            dp[i] = nums[i] + Math.min(dp[i - 1], 0);
            min = Math.min(min, dp[i]);
        }
        return Math.max(sum - min, max);
    }
}

※ product maximum subarray (medium)

Let's start with an intuitive idea. Like question 53 (maximum subarray sum), write the state transition equation:
d p [ n ] = m a x ( d p [ n − 1 ] ∗ n u m s [ n ] , n u m s [ n ] ) dp[n] = max(dp[n-1]*nums[n], nums[n]) dp[n]=max(dp[n−1]∗nums[n],nums[n])
Is there a problem with this writing? Obviously, there is a problem. For example: - 3,2, - 3. The result of the above equation is 2, but it is actually 18. The problem is that less negative is positive! The case of negative to positive is considered only when the current number is negative, and if the minimum negative number can be obtained in front, the multiplied result can be large; If it is a positive number, just consider the previous maximum value directly.

New state transition equation:
m a x a r r [ n ] = m a x ( n u m s [ n ] , m a x a r r [ n − 1 ] ∗ n u m s [ n ] , m i n a r r [ n − 1 ] ∗ n u m s [ n ] ) maxarr[n] = max(nums[n], maxarr[n-1] * nums[n], minarr[n-1] * nums[n]) maxarr[n]=max(nums[n],maxarr[n−1]∗nums[n],minarr[n−1]∗nums[n])
m i n a r r [ n ] = m i n ( n u m s [ n ] , m a x a r r [ n − 1 ] ∗ n u m s [ n ] , m i n i a r r [ n − 1 ] ∗ n u m s [ n ] ) minarr[n] = min(nums[n], maxarr[n-1] * nums[n], miniarr[n-1] *nums[n]) minarr[n]=min(nums[n],maxarr[n−1]∗nums[n],miniarr[n−1]∗nums[n])

maxarr[i] and minarr[i] represent the product of the largest and smallest arrays ending with the ith number.

class Solution {
    public int maxProduct(int[] nums) {
        // Adaptation of question 53
        int n = nums.length;
        int[] max_arr = new int[n];
        int[] min_arr = new int[n];
        max_arr[0] = nums[0];
        min_arr[0] = nums[0];
        // max_arr[i] refers to the maximum product of subarrays ending with the ith number
        // min_arr[i] refers to the minimum product of subarrays ending with the ith number
        // Considering a number nums[i] in the array, negative number * negative number and positive number * positive number need to be considered, and the maximum value must be generated between them
        int max = nums[0];
        for (int i = 1; i < n; i++) {
            max_arr[i] = Math.max(nums[i], Math.max(max_arr[i - 1] * nums[i], min_arr[i - 1] * nums[i]));
            min_arr[i] = Math.min(nums[i], Math.min(max_arr[i - 1] * nums[i], min_arr[i - 1] * nums[i]));
            max = Math.max(max_arr[i], max);
        }
        return max;
    }
}

※ the length of the longest subarray whose product is a positive number (medium +)

I didn't think of it for the first time, but I know it should be divided into positive and negative situations (the same as the previous question). Let's start the discussion:

Solution address: https://leetcode-cn.com/problems/maximum-length-of-subarray-with-positive-product/solution/cheng-ji-wei-zheng-shu-de-zui-chang-zi-shu-zu-ch-3/

Explanation of the above questions:
1. When num [i] > 0, the calculation of POS array: pos[i] = pos[i - 1] + 1. If pos[i - 1] = 0, it means that the product of continuous arrays ending with the I - 1st number is not positive (that is, it may be 0 or negative), but num [i] itself is a positive number, so it is + 1; If pos[i - 1]= 0, indicating that the product of the continuous array ending with the i - 1 number is positive, that is, "fair and aboveboard" to + 1. To sum up, regardless of the size of pos[i - 1], it can be written as pos[i] = pos[i - 1] + 1.

2. When num [i] > 0, the calculation of NEG array: why can't neg[i] = neg[i - 1] + 1 directly?, Because if neg[i - 1] = 0, it means that the product of the continuous array ending with the i - 1 number is non negative (may be positive and may be 0), and num [i] itself is a number greater than 0, which cannot be + 1 and should be 0. If neg[i - 1] > 0, it means that the product of continuous arrays ending with the i - 1 number is negative, and multiplying by a positive number is also negative, so neg[i] = neg[i - 1] + 1. To sum up, we need to judge the size of neg[i - 1] and write the corresponding state transition equation.

3. Similarly, neg[i] = pos[i - 1] + 1 can be used directly regardless of the size of pos[i - 1], because num [i] itself is less than 0. The update of pos[i] depends on neg[i - 1]. If neg[i - 1] > 0, it means that the product of continuous arrays ending in the I - 1 number is negative, and negative is positive, so pos[i] = neg[i - 1] + 1; If neg[i - 1] = 0, it means that the xxxx product is non negative (can be positive or 0). In addition, Num [i] itself is a negative number, so neg[i] = 0.

4. Finally, we need to discuss the case where num [i] = 0. Once it is 0, neg[i] pos[i] is 0, and 0 times any number = 0.

The meaning of neg and pos arrays: the maximum length of the product of subarrays ending with the ith number is negative and positive.

class Solution {
    public int getMaxLen(int[] nums) {
        int n = nums.length;
        int[] pos = new int[n];
        int[] neg = new int[n];
        if (nums[0] > 0) {
            pos[0] = 1;
        }
        if (nums[0] < 0) {
            neg[0] = 1;
        }
        // If the first number is 0, it is 0. The default array = 0
        int max = pos[0];
        for (int i = 1; i < n; i++) {
            if (nums[i] > 0) {
                pos[i] = pos[i - 1] + 1;
                if (neg[i - 1] > 0) {
                    neg[i] = neg[i - 1] + 1;
                }else {
                    neg[i] = 0;
                }
            } else if (nums[i] < 0) {
                // pos[i - 1] = 0 and > 0 are valid. Don't forget that this is the product
                neg[i] = pos[i - 1] + 1;
                if (neg[i - 1] > 0) {
                    // Negative is positive
                    pos[i] = neg[i - 1] + 1;
                } else {
                    // Nonnegative (can be positive, can be 0)
                    pos[i] = 0;
                }
            } else {
                // Current element = 0
                pos[i] = 0;
                neg[i] = 0;
            }
            // The longest subarray length with positive product was found
            max = Math.max(max, pos[i]);
        }
        return max;
    }
}

In case of product problem, we must discuss the positive and negative situation!

Best sightseeing combination (medium) (brain teaser)

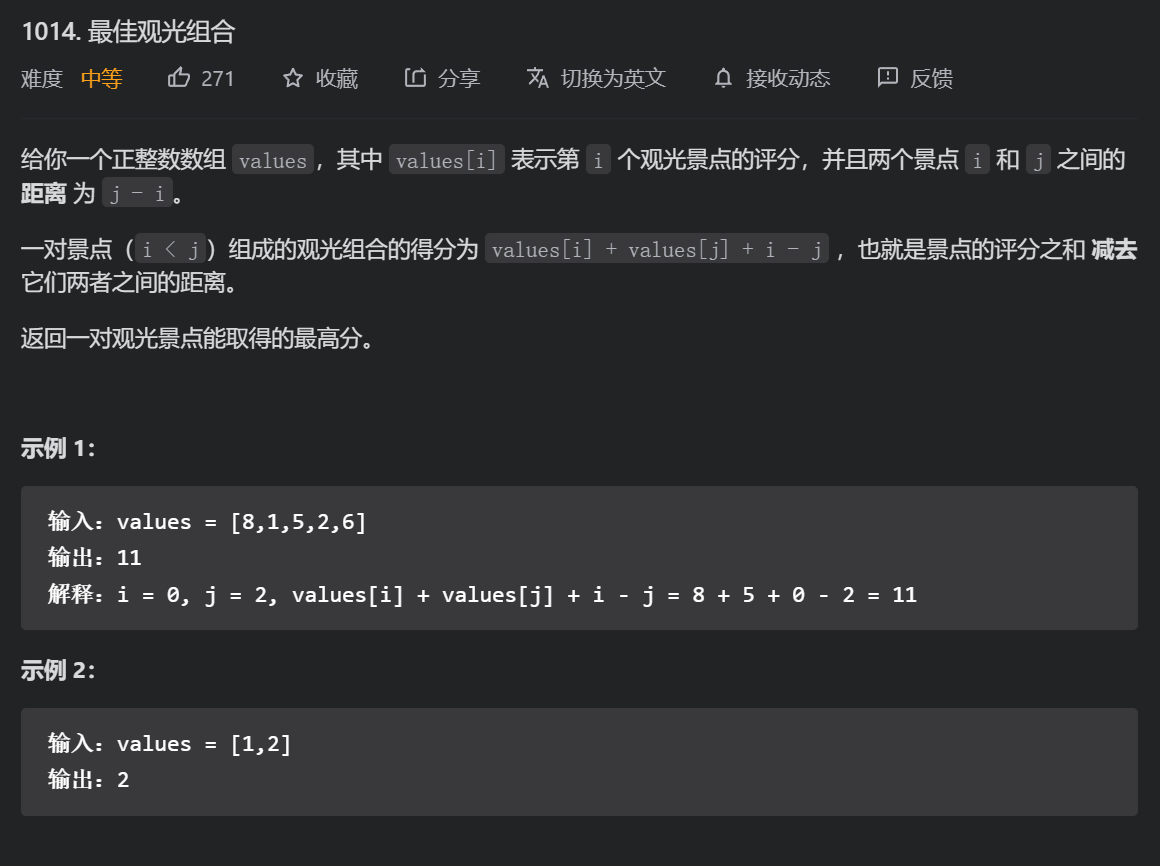
Split values[i] + values[j] + i - j into values[i] + i, values[j] - j. for the j-th scenic spot, values[j] - j is fixed, just find the maximum value of values[i] + i.

class Solution {
    public int maxScoreSightseeingPair(int[] values) {
        // Two scenic spots: I, j combination score = values[i] + values[j] - (j - i)
        // For classical j, its values[j] - j is fixed. Just find max(values[i] + i)
        // max(values[i] + i) can be obtained directly in the process of traversal
        int mx = values[0] + 0;
        int ans = 0;
        for (int i = 1; i < values.length; i++) {
            ans = Math.max(ans, values[i] - i + mx);
            mx = Math.max(mx, values[i] + i);
        }
        return ans;
    }
}

Continuous updating