Graph algorithm (array version)
1.1 shortest path Dijkstra algorithm:
- Suppose the vertices are \ (V_0 to V_5 \) six points. There is no connection at the beginning, but the edge weights between the vertices that can reach each other are known.
- The step is to start searching from vertex 0 each time, find the point with the shortest distance from the vertex, mark the point as true, and then query whether other points that can reach the point plus edge weight are smaller than the originally recorded distance value -- >, that is, update the shortest distance; After traversing all the points that can be reached from this point, return to the starting point again.
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXV=1000;
const int INF = 0x3f3f3f3f;//A large number
int n,m,s,G[MAXV][MAXV];//n is the number of vertices, m is the number of edges, and s is the starting point
int d[MAXV];//The shortest path length from the starting point to each point
bool vis[MAXV]={false}; //Mark the access array. false means no access, and true means accessed
/*Input of this question:
6 8 0 //6 8 vertices and 8 edges start at 0
0 1 1 The distance from 0 to 1 is 1
0 3 4
0 4 4
1 3 2
2 5 1
3 2 2
3 4 3
4 5 3
*/
void Dijkstra(int s){
fill(d,d+MAXV,INF);
d[s]=0; //Initialization operation
for(int i=0;i<n;i++){//After each update, return to the starting point and cycle n times
int u=-1,MIN=INF; //Compare the following, u makes d[u] minimum, and MIN stores the minimum d[u]
for(int j=0;j<n-1;j++){
if(vis[j]==false && d[j]<MIN){
u = j;
MIN = d[j];
}
}
if(u == -1) return;//The rest of the vertices and starting points s don't work
vis[u]= true;//Find the shortest point u from the starting point
for(int v=0;v<n;v++){//Start from u and update the shortest distance
if(vis[v]==false && G[u][v]!=INF && d[u]+G[u][v]<d[v]){//G[u][v] is the straight through distance from u to V vertex
d[v]=d[u]+G[u][v];
}
}
}
}
int main(){
int u,v,w;
cin>>n>>m>>s;
fill(G[0],G[0]+MAXV*MAXV,INF);
for(int i=0;i<m;i++){
cin>>u>>v>>w;
G[u][v]=w;
}
Dijkstra(s); // s
for(int i=0;i<n;i++){
cout<<d[i];//Output result shortest path
}
return 0;
}
1.2 basic formwork
//initialization
for(loop n second){
u = bring d[u]The label of the smallest vertex that has not been accessed;
remember u Accessed;
for(from u All the vertices that can be reached by departure v){
if(v Not accessed && with u Enable for mediation point s To vertex v Shortest distance d[v]Better){
optimization d[v];
}
2.1 storage of drawings
Storage of trees and graphs
Tree is a special graph, which is stored in the same way as graph.
For the edge ab in an undirected graph, two directed edges a - > b and B - > A are stored.
Therefore, we can only consider the storage of directed graphs.
(1) Adjacency matrix: g[a][b] storage edge a - > b
(2) Adjacency table:
//For each point K, open a single linked list to store K all the points that can be reached. h[k] stores the head node of the single linked list
int h[N], e[N], ne[N], idx;
// For each point K, open a single linked list to store K all the points that can be reached. h[k] stores the head node of the single linked list
// Add an edge a - > b
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// initialization
idx = 0;
memset(h, -1, sizeof h);
When the graph is an undirected graph with n points and m edges, M may be about twice as large as N:
In this case, let M = 2 * N
h[N] e[M],ne[M]
2.2 traversal of trees and graphs
Time complexity O(n+m),n represents the number of points, and M represents the number of edges
(1) Depth first traversal
int dfs(int u)
{
st[u] = true;
for(int i = h[u];i!= - 1;i = ne[i])
{
int j = e[i];
if(!st[j]) dfs(j);
}
}
(2) Width first traversal
queue<int> q;
st[1] = true;
q.push(1);
while(q.size())
{
int t = q.front();
q.pop();
for(int i = h[t];h!=-1;i = ne[i])
{
int j = e[i];
if(!st[j])
{
st[j] = true;
q.push(j);
}
}
}
Shortest path algorithm
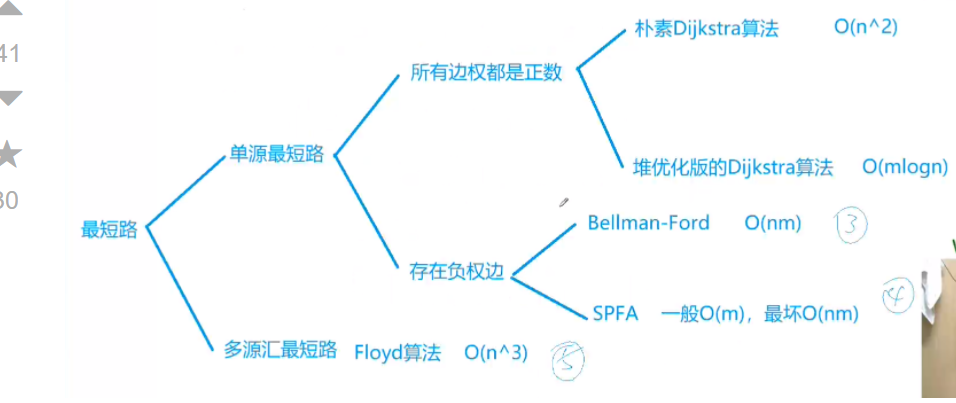
3.dijkstra algorithm
- The naive dijkstra algorithm is suitable for dense graphs and is stored by adjacency matrix
- Heap optimized version is suitable for sparse graph, and the range of storage points with adjacency table is large -- sparse graph
3.1 naive \ (dijkstra \) algorithm
The time complexity is \ (O(n^2+m)\), n represents the number of points, and M represents the number of edges
1. When a time point is reached, the shortest distance of some points on the graph has been determined, and the shortest distance of some points has not been determined.
2. Select the point closest to the source point among all undetermined points and consider it as the shortest distance.
3. Then traverse all the outgoing edges of this point and update all the points.
Algorithm design: greedy
int g[N][N]; // Store each edge
int dist[N]; // Store the shortest distance from point 1 to each point
bool st[N]; // Store whether the shortest circuit of each point has been determined
// Find the shortest circuit from point 1 to point n. if it does not exist, return - 1
// The coordinates of the point are from 1 to n
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0; // Find the distance from point 1 to other points, and mark dist[1] = 0
// Traverse other points
for (int i = 0; i < n - 1; i ++ ) { // Just cycle n-1 times, no other meaning
int t = -1;
// Find the point with the smallest distance among the points that have not been used to update the shortest path
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j])) // t==-1 is used to determine the remaining first point not used for update
t = j;
// Update the distance of other points with t
for (int j = 1; j <= n; j ++ )
// if(!st[j]) can be written or not
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
St [] more precisely means whether a point has updated other points, and whether the st shortest path has been determined rather than whether its shortest distance has been determined. Therefore, when updating the distance of other points, the previously updated points should also be updated. In fact, if(!st[j]) can also be added
3.2 heap optimization dijkstra algorithm
Idea:
A point in set S indicates that the shortest path has been found
Heap optimized dijkstra It's a simple version dijkstra Optimized in the plain version dijkstra The point with the highest time complexity is to find the point with the shortest distance O(n^2)Minimum heap optimization can be used.
1. The distance of point 1 is initialized to zero, and the other points are initialized to infinity.
2. Put point one in the heap.
3. Keep cycling until the heap is empty. The operations performed in each cycle are:
Pop up the top of the stack (with the plain version) diijkstra find S The point with the shortest outer distance is the same, and the shortest path marking the point has been determined).
Use this point to update the distance of the critical point. If the update is successful, it will be added to the heap.
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 150010;
// Sparse graphs are stored by adjacency matrix
int h[N], e[N], ne[N], idx;
int w[N], dist[N];
bool st[N];
int n, m;
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = h[a];
w[idx] = c; // The weight of the edges,
// It doesn't matter if there are multiple edges. Suppose 1 - > 2 has edges with weights of 2 and 3. When traversing to point 1, the distance of point 2 will be updated twice and put into the heap
h[a] = idx++;
}
int dijkstra() {
memset(dist, 0x3f, sizeof dist);
priority_queue<PII, vector<PII>, greater<PII>> heap;
dist[1] = 0;
heap.push({0,1}); // Put the initial value into the small root pile distance -- point
while(heap.size()) {
PII k = heap.top(); // Take the point with the shortest distance not in the set S, and the set S represents the set of points with the shortest path determined
heap.pop();
int v = k.second, distance = k.first;
if(st[v]) continue;
st[v] = true;
// Take v as the starting point and traverse the adjacent points of v
for(int i = h[v]; i != -1; i = ne[i]) {
int j = e[i];
if(dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n,&m);
while(m--) {
int x,y,c;
scanf("%d%d%d", &x,&y,&c);
add(x,y,c);
}
cout << dijkstra() << endl;
return 0;
}
Some questions:
- When updating dist, two points may be repeatedly added to the heap. Some points are both the adjacency points of a and b. such points may be added once when updating the adjacency points of a and once again when updating the adjacency points of b. in this way, there are two identical points in the queue. Although the distances are different, the st array is used to mark the points that have found the shortest path, Avoid double counting
4. \ (Bellman Ford \) algorithm
Title: Shortest path with edge limita
Single source shortest path algorithm
For weighted digraph G = (V, E), Dijkstra algorithm requires that the weights of edges in graph G are non negative, and Bellman Ford algorithm A well implemented Dijkstra algorithm has lower running time than Bellman Ford algorithm.
Design: dynamic programming
Time complexity: \ (O(V*E) \) vertex number, edge number, \ (n vertex number, m edge number \)
Understanding: relax all edges \ (n-1 \) times, because in a graph with n vertices, the shortest path between any two points contains at most n-1 edges,
In other words, after all edges are relaxed in the first round, the shortest distance from the source point to other vertices through at most one edge is obtained;
In the second round, after relaxing all edges, the shortest distance from the source point to other vertices through up to 2 edges is obtained;
Algorithm description:
1. The \ (dist[N] \) array represents the distance from the source vertex to all vertices, initialized as \ (infinte\),\(dist[1][1]=0 \),
2. Calculate the shortest path and perform \ (V-1 \) traversals
For each edge in the graph: if the distance d from the start point to u plus the weight w is less than the distance to the end point v, the distance D of the end point v is updated
\(if(dist[b]>dist[a]+w) dist[b]=dist[a]+w\)
For example, by adding a copy array, you can find the shortest distance through up to k edges
int n, m; // n represents the number of points and m represents the number of sides
int dist[N]; // dist[x] stores the shortest distance from 1 to X
int backup[N]; // Copy the array to ensure that the number of rounds is consistent with the number of sides
struct Edge // Edge, a represents the point, b represents the entry point, and w represents the weight of the edge
{
int a, b, w;
}edges[M];
// Find the shortest distance from 1 to n. if you can't go from 1 to n, return - 1.
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
// Initially, the distance from point 1 to other points is inf
dist[1] = 0;
// If the n-th iteration still relaxes the trigonometric inequality, it indicates that there is a shortest path with a length of n+1. According to the drawer principle, there are at least two identical points in the path, indicating that there is a negative weight loop in the graph.
for (int i = 0; i < n; i ++ )
{
memcpy(backup,dist,sizeof dist); // Copy the array, because updating other points will affect the update information of other points
for (int j = 0; j < m; j ++ ) // Traverse each edge
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > backup[a] + w)
dist[b] = backup[a] + w;
}
}
if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}
Judge whether there is a negative weight ring, and then perform an additional traversal of the edge. If it can be updated, it indicates that there is still an edge, making the distance between two points shorter. In fact, it is updated many times.
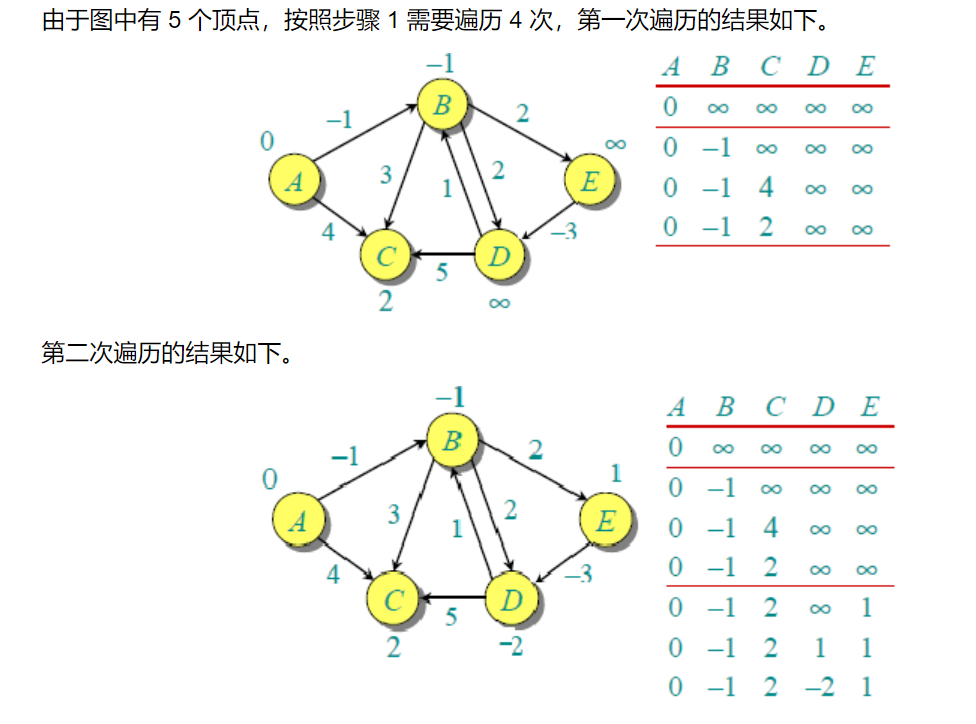
be careful:
-
If the number of edges is not limited, the shortest path is found directly, and there is no need to copy the array
-
If you limit the number of edges, you need to copy the array
-
Why > 0x3f3f3f3f / 2 (mainly because each edge is traversed, and many useless edges are traversed)
-

5. \ (SPFA \) algorithm
Title: spafa judging negative ring
spfa finding the shortest path
https://blog.csdn.net/qq_35644234/article/details/61614581 This blog shows the process
https://www.cnblogs.com/acioi/p/11694294.html Explanation of spfa finding negative rings
Time complexity average case \ (O(m) \), worst case \ (O(nm)\), n represents the number of points, and M represents the number of edges
\(SPFA algorithm \) is a queue optimization for the above \ (bellmanford \) algorithm
Algorithm description: first, a queue is established. There are only starting points in the initial queue. A table is established to record the shortest path from the starting point to all points (the initial value is assigned to the maximum value), and then the relaxation operation is carried out. The points in the queue are used to refresh the shortest path from the starting point to all points in turn. If the refresh is successful and the refreshed point is not in the queue, it is added to the queue.
Find negative ring: if a point enters the queue more than N times, there is a negative ring (N is the number of vertices of the graph)
Optimal solution: use a cnt[i] array to record the number of points passing on the shortest path to point I. If cnt[i] > n appears, it indicates that a negative ring appears. The number of edges can also be counted. When the number of edges > = n, there is also a negative ring.
The st array is only used to record which points are currently in the queue
int n; // Total points
int h[N],w[N],e[N],ne[N],idx; // The adjacency table stores all edges
int dist[N];
bool st[N];// Stores whether each point is in the queue
// Find the shortest distance from point 1 to point n. if you can't walk from point 1 to point n, return - 1
int spfa()
{
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
// Take out an element in the queue to update the distance
while(q.size())
{
auto t = q.front();
q.pop();
st[t] = false; // The pop-up queue is marked as false because there may be updates later
for(int i = h[t];i != -1;i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t]+w[i])
{
// Update the shortest distance first
dist[j] = dist[t] + w[i];
// If the updated point is not in the queue, it needs to be added, because its minimum value needs to be used later
if(!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
5. \ (Floyd \) algorithm
\(Floyd \) algorithm belongs to violent solution. The time complexity \ (O(n^3)\),\(n \) represents the number of points
// initialization
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
{
d[i][j] = (i == j ? 0 : INF);
}
// After the algorithm, d[a][b] represents the shortest distance from a to B
void floyd()
{
for (int k = 1; k <= n; k ++ ) // z
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
if(g[l][r] > inf / 2) cout << "impossible" << endl;
else cout << g[l][r] << endl;
- The method to judge that there is no shortest path is > inf / 2. Reason: add the distance of 1 ~ 6 points, and 6 is the end point,
d[1][5] = 0x3f, 1 to 5 are unreachable, at this time, d [5] [6] = - 4, d [1] [6] = D [1] [5] + D [5] [6]= 0x3f but greater than 0x3f/2. At this time, 1 to 6 are unreachable.
6. Topological sequences of directed acyclic graphs
Title: Topological sequences of directed acyclic graphs
In graph theory, topological ordering is a linear sequence of all vertices of a directed acyclic graph:
1. Once per vertex
2. If there is a path from a to B, vertex A is in front of B in the sequence.
A directed acyclic graph must have at least one point with degree 0
How to find topological sequence?
- In the topology sequence, all edges are from front to back, so the points with a degree of 0 can be used as the starting point, and all points with a degree of 0 can be queued, because there is no point in front of it, it can only point to the point behind it
- After joining the team, subtract 1 from the entry at the end it points to
Join the team at points with a penetration of 0
queue<int> q;
for(int i = 1;i <= n;i++) {
if(!d[i]) q.push(i);
}
Traverse all outgoing edges of t
for(int i = h[t]; i!=-1;i = ne[i]) {
int j = e[i];
}
Complete template
bool f() {
int q[N], hh = 0, tt = -1;
for(int i = 1; i < n;i++) {
if(!d[i]) q[++tt] = i; // Join the team
}
while(hh <= tt) {
int t = q[hh++];
// Traverse the end of t
for(int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
d[j]--;
if(!d[j]) q[++tt] = j;
}
}
return tt == n - 1; // Are all points in the team? Otherwise, it indicates that there is a ring in the figure
}