catalogue
Question 1: how to add one to all node values of a binary tree?
Question 2: how does Leetcode 100 judge whether two binary trees are the same?
Question 3: judge whether a tree is a sort binary tree
Question 4: serialize and deserialize a binary tree
Question 1: how to collect change
algorithm
Tree traversal
Question 1: how to add one to all node values of a binary tree?
In other words, traverse each node, and then each node value + 1;
The implementation method is tree traversal: [pre, middle and post order traversal]
public void traverseHelper(MyNode node){
if (node==null){
return;
}
//Preorder traversal
traverseHelper(node.left);
//Medium order traversal
traverseHelper(node.right);
//Subsequent traversal
}So the answer to question 1 is:
public void NodePlus(TreeNode node) {
if (node == null) {
return;
}
//node.value = node.value + 1;
NodePlus(node.left);
//node.value = node.value + 1;
NodePlus(node.right);
node.value = node.value + 1;
}Question 2: how does Leetcode 100 judge whether two binary trees are the same?
The idea of this problem is the traversal of the tree, but the judgment conditions are added on the basis of traversal. Comparing one or two questions, we can summarize the method of tree traversal: recursion
The solution to question 2 is:
public static boolean isSameBST(TreeNode one, TreeNode two) {
if (one == null && two == null) {
return true;
}
if (one == null || two == null) {
return false;
}
if (one.value != two.value) {
return false;
}
// The above is the judgment condition, and the following two recursive statements are the core of tree traversal
boolean s1 = isSameBST(one.left, two.left);
boolean s2 = isSameBST(one.right, two.right);
return s1 && s2;
}
// Test class
public static void main(String[] args) {
TreeNode node1 = new TreeNode(2);
node1.left = new TreeNode(1);
node1.right = new TreeNode(2);
TreeNode node2 = new TreeNode(2);
node2.left = new TreeNode(1);
node2.right = new TreeNode(3);
System.out.println(isSameBST(node1, node2));
}Question 3: judge whether a tree is a sort binary tree
LeetCode: 98. Validate binary search tree
A valid binary search tree is defined as follows:
-
The left subtree of a node contains only the number less than the current node.
-
The right subtree of a node contains only a number greater than the current node.
-
All left and right subtrees themselves must also be binary search trees.
Idea: the traversal of the tree takes the value of the parent node when traversing each node, so the bstHelper method is required to provide the information of the parent node.
public static boolean isBST(TreeNode treeNode) {
return bstHelper(treeNode, null, null);
}
private static boolean bstHelper(TreeNode currentNode, TreeNode maxNode, TreeNode minNode) {
if (currentNode == null) {
return true;
}
if (maxNode != null && currentNode.value => maxNode.value) {
return false;
}
if (minNode!=null &¤tNode.value <= minNode.value) {
return false;
}
boolean b1 = bstHelper(currentNode.left, currentNode, minNode);
boolean b2 = bstHelper(currentNode.right, maxNode, currentNode);
return b1 && b2;
}
// Test class
public static void main(String[] args) {
TreeNode node = new TreeNode(2);
node.left = new TreeNode(1);
node.right = new TreeNode(4);
System.out.println(isBST(node));
}Question 4: serialize and deserialize a binary tree
Sword finger Offer 37 Serialized binary tree
A binary tree can be serialized into a string, and the string can be deserialized into the original tree structure.
Key: the tree structure cannot be determined only through one sorting algorithm. Two traversals are required to determine the tree structure [front, middle, front and back]
Conclusion: add the flag of empty subtree when serializing
private static LinkedList<Integer> list = new LinkedList<>();
// Serialization: traverse each node value and store it in the linkedList
public static void serialize(TreeNode node){
if (node==null){
list.add(-1);
return;
}
list.add(node.value);
serialize(node.left);
serialize(node.right);
}
// Deserialization: retrieve the value from the linkedList and restore it to a tree
public static TreeNode deSerialize(LinkedList<Integer> deList){
Integer first = deList.removeFirst();
if (first==-1){
return null;
}
TreeNode node = new TreeNode(first);
node.left = deSerialize(deList);
node.right = deSerialize(deList);
return node;
}
// Test class
public static void main(String[] args) {
// Use balanced binary tree (code implementation in the previous article)
AVLTree tree = new AVLTree();
tree.insert(new TreeNode(2));
tree.insert(new TreeNode(1));
tree.insert(new TreeNode(3));
tree.insert(new TreeNode(6));
tree.insert(new TreeNode(10));
serialize(tree.getRoot());
TreeNode node = deSerialize(list);
tree.traverse(node); //Middle order traversal is used here, so the output result is 1 2 3 6 10
}dynamic programming
Application scenario: it is generally a problem of trying to find the best value
Three elements: overlapping subproblem, optimal substructure and state transition equation
Core: first cite all the cases, then optimize the problem and mathematical induction
Example: Fibonacci sequence
/**
* Fibonacci sequence
*
* Definition: starting from item 3, each item is equal to the sum of the first two items
*/
public static int simpleFib(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
/**
* This method (violent recursion) will cause overlapping subproblems
* For example, when n = 4, calculate the values of n = 3 and n = 2
* n = 3 When, calculate the values of n = 2 and n = 1
* The problem of n = 2 is repeated
*/
return simpleFib(n - 1) + simpleFib(n - 2);
}[overlapping sub questions]:
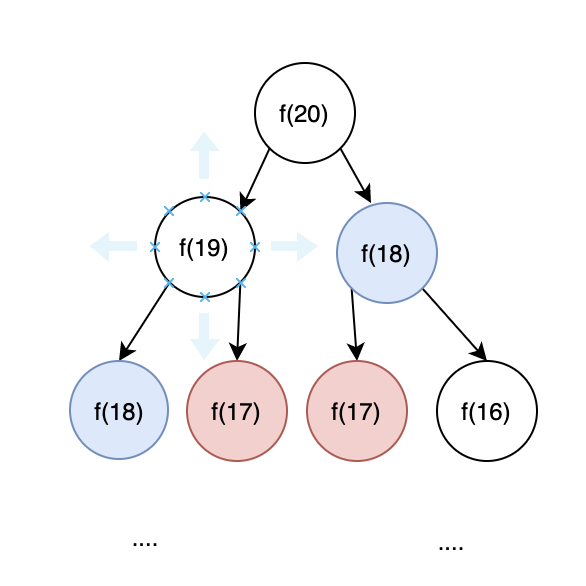
Time complexity of violent recursive algorithm: number of subproblems * time required to solve a subproblem O(2^n)
Optimize the above overlapping subproblems: store the subproblem results
public static int cacheFib(int n) {
// Store the sub problem results in the HashMap
Map<Integer, Integer> cache = new HashMap<>();
return fibHelper(n, cache);
}
private static int fibHelper(int n, Map<Integer, Integer> cache) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
Integer val = cache.get(n);
if (val != null) {
return val;
}
int i = fibHelper(n - 1, cache) + fibHelper(n - 2, cache);
cache.put(n, i);
return i;
}After optimization, the time complexity returns to constant level O(1)
Another question, what is the state transition equation?
[state transition equation]: think of f(n) as a state, then this state is obtained through the state transition of n-1 and n-2.
simpleFib(n) = simpleFib(n - 1) + simpleFib(n - 2);
Question 1: how to collect change
LeetCode: 322. Change
Give you an integer array of coins, which represents coins of different denominations; And an integer amount representing the total amount.
Calculate and return the minimum number of coins required to make up the total amount. If no coin combination can make up the total amount, return - 1.
Example:
count = 11;coins{ 1, 2, 5 }
Law finding:
| coin = 1 | coin = 2 | coin = 5 | |
|---|---|---|---|
| 1 | 1 (1 * 1) | ||
| 2 | 2 (1 * 2) | 1 (2 * 1) | |
| 3 | 3 (1 * 3) | 2 (2 * 1 + 1 * 1) | |
| 4 | 4 (1 * 4) | 2 (2 * 2) | |
| 5 | 5 (1 * 5) | 2 (2 * 2 + 1 * 1) | 1 (5 * 1) |
| 6 | 6 (1 * 6) | 3 (2 * 3) | 2 (5 * 1 + 1 * 1) |
| 7 | 7 (1 * 7) | 4 (2 * 3 + 1 * 1) | 2 (5 * 1 + 2 * 1) |
| 8 | 8 (1 * 8) | 4 (2 * 4) | 3 (5 * 1 + 2 * 1 + 1 * 1) |
| 9 | 9 (1 * 9) | 5 (2 * 4 + 1 * 1) | 3 (5 * 1 + 2 * 2) |
| 10 | 10 (1 * 10) | 5 (2 * 5) | 2 (5 * 2) |
| 11 | 11 (1 * 11) | 6 (2 * 5 + 1 * 1) | 3 (5 * 2 + 1 * 1) |
To find the minimum number of coins with an amount of 11, you only need to find the minimum number of coins with an amount of 10 (2) and then add 1 = 3
Similarly, if you want to find the minimum number of coins with an amount of 8, you only need to find the minimum number of coins with an amount of 7 (2) and then add 1 = 3
[optimal substructure]: a structure with independent states and optimal solutions among subproblems
public static int coinsChange(int[] coins, int totalMoney) {
// Dynamic programming has: boundary problem
if (coins.length == 0) {
return -1;
}
// The array is used to store the minimum number of coins per count
int[] memo = new int[totalMoney + 1];
memo[0] = 0;
// The first cycle is count total amount cycle
for (int i = 1; i <= totalMoney; i++) {
int min = Integer.MAX_VALUE;
// The second cycle is coin denomination cycle
for (int j = 0; j < coins.length; j++) {
int k = i - coins[j];
if (k >= 0 && memo[k] < min) {
// To find the minimum number of coins with an amount of 11,
// Only the minimum number of coins with an amount of 10 is required, and then + 1
min = memo[k] + 1;
}
}
memo[i] = min;
}
return memo[totalMoney] == Integer.MAX_VALUE ? -1 : memo[totalMoney];
}