Application conditions

This blog summarizes and reflects on the MOOC course of data structure and algorithm by Chen Bin of Peking University.

Recursion is an elegant way to understand problems, and it is also a place where I was confused in the process of learning.

To understand recursion, keep in mind the three elements of recursive application:

1. Basic end condition

2. Reduce the scale of the problem

3. Call itself

The advantages and disadvantages of recursion are also obvious. The advantages are: it can certainly find the optimal solution; Disadvantages: low efficiency (too many repeated calculations)

case analysis

This blog analyzes a classic application scenario "change problem", and gives its own solution and teacher Chen Bin's solution respectively to help analyze and understand recursion

Problem description

The minimum number of currencies for change in a monetary system

Solution sharing

Analyze the problem and firmly start from the three elements.

Basic end condition: the change is exactly a denomination in the monetary system, and 1 is returned;

Reduce the scale of the problem and call itself: after the change minus a denomination, find the minimum number of coins to exchange (call itself recursively);

My solution is as follows:

def OddChange(valuelist, change):
    if change in valuelist:
        return 1
    elif change >= 25:
        return min(1 + OddChange(valuelist, change - 1), 1 + OddChange(valuelist, change - 5),
                   1 + OddChange(valuelist, change - 10), 1 + OddChange(valuelist, change - 25))
    elif change >= 10:
        return min(1 + OddChange(valuelist, change - 1), 1 + OddChange(valuelist, change - 5),
                   1 + OddChange(valuelist, change - 10))
    elif change >= 5:
        return min(1 + OddChange(valuelist, change - 1), 1 + OddChange(valuelist, change - 5))
    else:
        return 1 + OddChange(valuelist, change - 1)

Mr. Chen Bin's solution is as follows:

def recMC(coinValueList, change):
    minCoins = change
    # Minimum size, direct return
    if change in coinValueList:
        return 1
    else:
        for i in [c for c in coinValueList if c <= change]:
            # Reduce the scale and call itself
            numCoins = 1 + recMC(coinValueList, change - i)
            if numCoins < minCoins:
                minCoins = numCoins
    return minCoins

Analyze the time cost using timeit as follows:

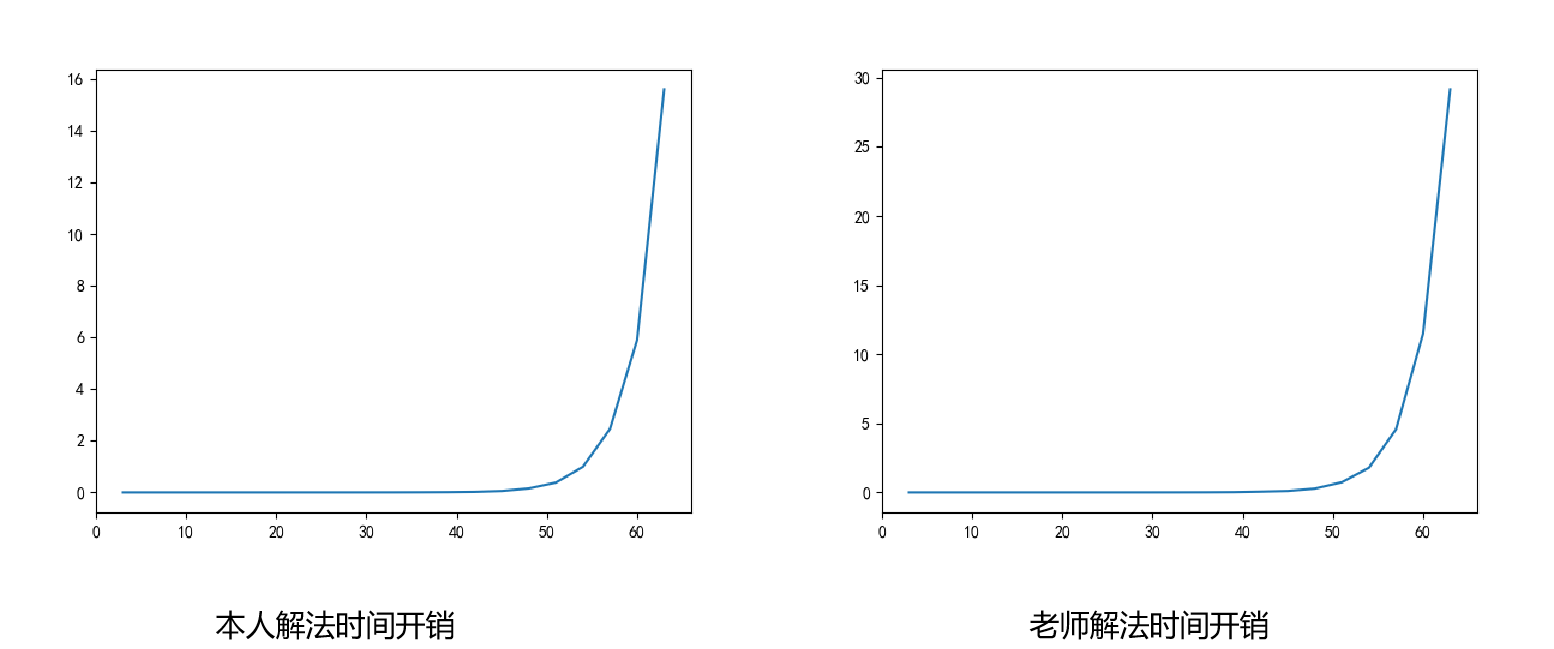
• It is obvious that the time cost of the two solutions increases exponentially, which confirms the previous view of * * low efficiency (too many repeated calculations) * *
• The teacher's writing is more elegant and can be learned, but the for loop reduces the speed to a certain extent
• Taking 63 change as an example, the total number of recursions I calculated is 67716925

Solution improvement

I think this part is a sublimation for me. The previous time cost makes me think that the recursive algorithm is a very unreliable algorithm. After all, a 63 change takes 30s +, which is unbearable. However, with the knowledge of the idea of "space for time", this algorithm can be solved instantly.

The optimal solution obtained in the recursive call process is recorded. Before recursive call, first look up whether there is an optimal solution of partial change in the table. If yes, the optimal solution is returned directly without recursive call; If not, the recursive call is made.

In terms of implementation, my first reaction is to save using a dictionary:

def OddChangeOp(valuelist, change,resultdic):
    if change in valuelist:
        resultdic[str(change)] = 1
        return 1
    elif str(change) in resultdic:
        return resultdic[str(change)]
    elif change >= 25:
        resultdic[str(change)] = min(1 + OddChangeOp(valuelist, change - 1,resultdic), 1 + OddChangeOp(valuelist, change - 5,resultdic),
                   1 + OddChangeOp(valuelist, change - 10,resultdic), 1 + OddChangeOp(valuelist, change - 25,resultdic))
        return resultdic[str(change)]
    elif change >= 10:
        resultdic[str(change)] = min(1 + OddChangeOp(valuelist, change - 1,resultdic), 1 + OddChangeOp(valuelist, change - 5,resultdic),
                   1 + OddChangeOp(valuelist, change - 10,resultdic))
        return resultdic[str(change)]
    elif change >= 5:
        resultdic[str(change)] = min(1 + OddChangeOp(valuelist, change - 1,resultdic), 1 + OddChangeOp(valuelist, change - 5,resultdic))
        return resultdic[str(change)]
    else:
        resultdic[str(change)] = 1 + OddChangeOp(valuelist, change - 1,resultdic)
        return resultdic[str(change)]

However, the teacher's solution is more interesting. I directly use the list to complete the same work. My purpose of using the dictionary is to build a mapping relationship, but the list itself also has a mapping relationship, that is, the subscript of the list and the value of the list

def recDC(coinValuelist, change, knowResults):
    minCoins = change
    # Recursive basic end conditions, record the optimal solution
    if change in coinValuelist:
        knowResults[change] = 1
        return 1
    # Look up the table successfully and use the optimal solution directly
    elif knowResults[change] > 0:
        return knowResults[change]
    else:
        for i in [c for c in coinValuelist if c <= change]:
            numCoins = 1 + recDC(coinValuelist, change - i, knowResults)
            if numCoins < minCoins:
                minCoins = numCoins
                # Find the optimal solution and record it in the table
            knowResults[change] = minCoins
    return minCoins

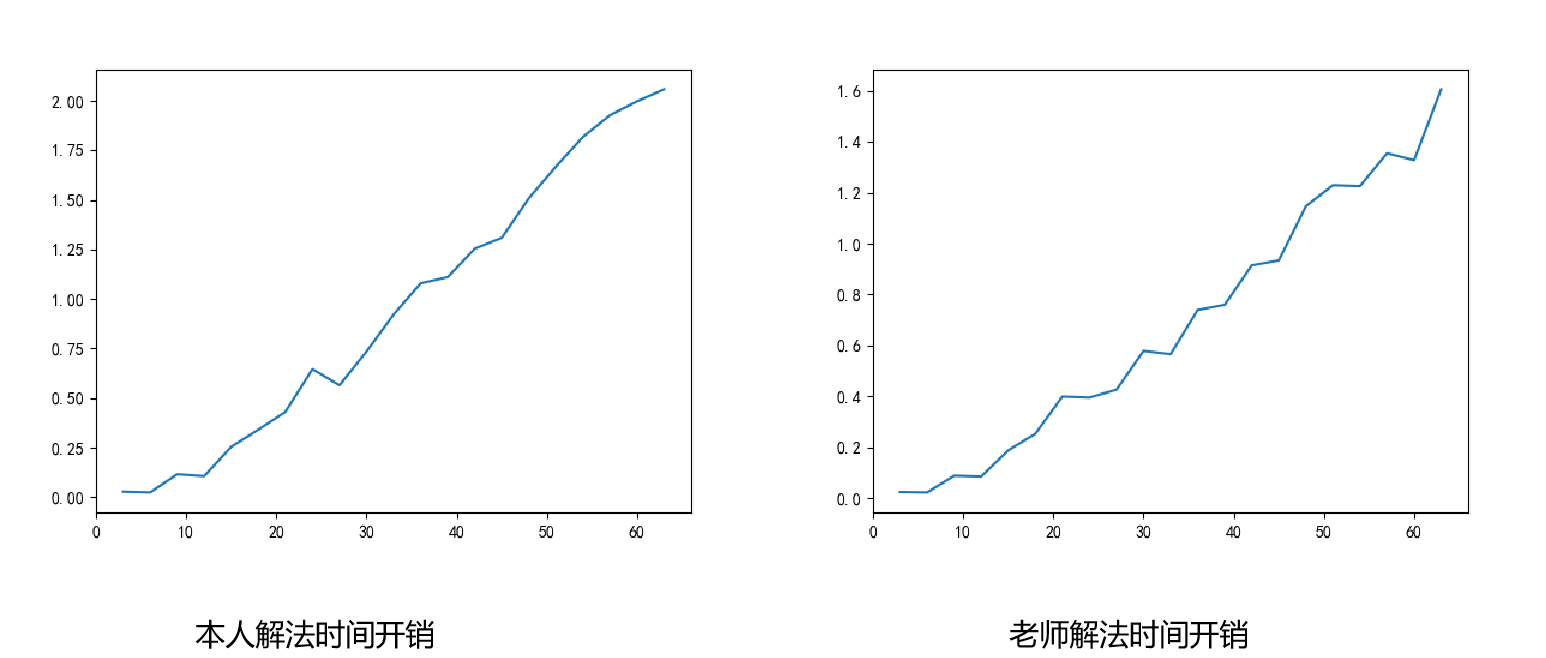
Compared with the time cost, it can be found that the solution is almost completed in an instant. The figure below shows the time-consuming of calling 10000 times. Moreover, the scheme in which the teacher directly uses the list to construct the mapping to store the optimal solution takes much less time than my solution.

At the same time, the algorithm is approximately linear, the time overhead and memory overhead are not particularly high. The real available algorithms are really amazing!!

Calculation of recursion times

Finally, an interesting thing to share is the number of iterations to solve the recursive algorithm, which has some advantages in implementation Three methods can be selected

• global variable

• Function built-in properties

• Decorator

Among them, the decorator method is simply too elegant. Of course, it is also because of my lack of python high-level syntax

mark here to record

class Counter(object) :
    def __init__(self, fun) :
        self._fun = fun
        self.counter=0
    def __call__(self,*args, **kwargs) :
        self.counter += 1
        return self._fun(*args, **kwargs)


@Counter
def OddChange(valuelist, change):

In the end, after introducing the storage mechanism into the iterative algorithm, I instantly felt invincible! The charm of the algorithm is infinite, which can not be realized simply by looking at other people's wheels.