1, Time complexity
The number of constant operations to be performed by the algorithm according to the worst performance, leaving only the highest order term and removing the coefficients
2, Bubble sort, select sort, and insert sort
The three simplest sorting algorithms are time complexity O(N^2) and space complexity O(1)
Bubble sort:
public static void bubbleSort(int[] a) {
for (int i = 0; i < a.length; i++) {
for (int j = a.length - 1; j > i; j--) {
if (a[j] < a[j - 1]) {
swap(a, j - 1, j);
}
}
}
}
Select sort:
public static void selectSort(int[] a) {
for (int i = 0; i < a.length; i++) {
for (int j = i + 1; j < a.length; j++) {
if (a[i] > a[j]) {
swap(a, i, j);
}
}
}
}
Insert sort:
It is equivalent to the process of playing cards and touching cards, which is slightly faster than selection and bubbling
public static int[] insertSort(int[] a){
for (int i = 0; i < a.length; i++){
for (int j = i; j > 0 && a[j-1] > a[j]; j--){
swap(a,j-1,j);
}
}
return a;
}
3, swap function and or
swap function
Normal swap function:
public static void swap(int[] arr, int a, int b) {
int c = arr[a];
arr[a] = arr[b];
arr[b] = c;
}
Alternatively, the swap function can be implemented without additional space (provided that a and B cannot point to the same memory block, that is, a! = b):
public static void swap(int[] arr, int a, int b) {
array[a] = array[a] ^ array[b];
array[b] = array[a] ^ array[b];
array[a] = array[a] ^ array[b];
}
Or
Or the same is 0, the difference is 1, and two binary numbers can also be considered as non carry addition.
Or the nature of:
1)0 ^ N=N; N ^ N=0
2) Satisfy commutative law and associative law: a ^ b=b^ a; a ^ b ^ c=a ^ (b ^ c)
3) A set of data or, independent of the order of or
Relevant examples:
Example 1. In an array, one number appears odd times, and the other numbers appear even times. Find the number that appears odd times.
public static int method1(int[] arraylist){
int eor = 0;
//Using the property of or, the number in the array can be or once
for (int i=0;i< arraylist.length;i++) {
eor ^= arraylist[i];
}
return eor;
}
Example 2: in an array, two numbers appear odd times, and the other numbers appear even times. Find the two numbers that appear odd times.
public static int[] method2(int[] arraylist){
int eor = 0;
for (int i=0;i< arraylist.length;i++) {
eor ^= arraylist[i];
}
/*
eor=a^b
a!=b
eor!=0
eor There must be a position of 1
This indicates that one of the bits a and b is 1 and the other is 0
*/
int rightone = 0;
//Take the rightmost bit of 1
rightone = eor&(~eor+1);
int onlyone = 0;
for (int i=0;i< arraylist.length;i++) {
if ((arraylist[i] & rightone) == 0) {
onlyone ^= arraylist[i];
}
}
int[] b = new int[2];
b[0] = onlyone;
b[1] = eor^onlyone;
return b;
}
4, Dichotomy
Example 1. An ordered array determines whether a number exists in the array. If it exists, the array subscript is returned. If it does not exist, the - 1 is returned
public static int bisectionMethod1(int a[], int b){
int front = 0;
int end = a.length-1;
int mid = (front + end)/2;
while (front <= end){
if(a[mid] == b){
return mid;
}else if(a[mid] < b) {
front = mid+1;
mid = (front + end)/2;
}else {
end = mid-1;
mid = (front + end)/2;
}
}
return -1;
}
Example 2: an ordered array determines whether a number exists in the array. If it exists, it returns the subscript of the first existing number. If it does not exist, it returns - 1
public static int bisectionMethod2(int a[], int b){
int front = 0;
int end = a.length-1;
int mid = (front + end)/2;
int tag = -1;
while (front <= end){
if(a[mid] > b){
end = mid-1;
mid = (front + end)/2;
}else if(a[mid] < b){
front = mid+1;
mid = (front + end)/2;
}else {
tag = mid;
end = mid-1;
mid = (front + end)/2;
}
}
return tag;
}
Example 3. To find the local minimum value, an unordered array must have two adjacent numbers that are not equal. Find a number in this array that is smaller than the adjacent numbers. If there is a subscript, if there is no subscript, return - 1. The time complexity is required to be within O(logN) (not necessarily an ordered array can be divided in two)
public static int bisectionMethod3(int a[]){
int front = 0;
int end = a.length-1;
int mid = (front + end)/2;
if(a.length == 1){
return 0;
}
if(a[front] < a[front+1]){
return front;
}else if(a[end] < a[end-1]){
return end;
}else {
while(front <= end){
if(a[mid] > a[front]){
end = mid -1;
mid = (front + end)/2;
}else if(a[mid] > a[end]){
front = mid +1;
mid = (front + end)/2;
}else {
if(a[mid] > a[mid-1]){
end = mid-1;
mid = (front + end)/2;
}
else if(a[mid] > a[mid+1]) {
front = mid + 1;
mid = (front + end) / 2;
}else {
return mid;
}
}
}
}
return -1;
}
5, master formula
If a recursive algorithm can be expressed as:
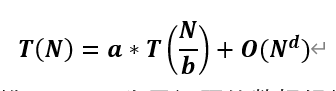
Where T(N) is the data scale of the parent problem, T(N/b) is the data scale of the sub problem, a is the execution times of the sub problem, and O(N^d) is the time complexity of the remaining execution parts.
Then the time complexity of this algorithm can be calculated directly
1) If log (B, a) > D - > time complexity is O(N^log(b,a))
2) If log (B, a) = D - > time complexity is O((N^d)*logN)
3) If log (B, a) < D - > time complexity is O(N^d)
6, Merge sort
Process: first, the first half and the second half of the upper array are ordered respectively, and then the two halves are merged (recursive)
Merge sort is external sort (with the help of the sorting algorithm of external array)
public static void mergeSort(int[] arr, int front, int end){
if(end == front){
return ;
}
int mid = front + ((end - front)>>1);
mergeSort(arr, front, mid);
mergeSort(arr, mid + 1, end);
merge(arr, front,mid , end);
}
public static void merge(int[] arr, int front,int mid, int end){
int[] help = new int[end - front + 1];
int p = front;
int q = mid + 1;
int i = 0;
while (p <= mid && q <= end){
//Replace if else with ternary operator
help[i++] = arr[p] > arr[q] ? arr[q++] : arr[p++];
}
while (p <= mid){
help[i++] = arr[p++];
}
while (q <= end){
help[i++] = arr[q++];
}
for(i = 0; i < help.length; i++){
arr[front + i] = help[i];
}
}
The merging and sorting conforms to the master formula. The calculation time complexity is O(NlogN) and the additional space complexity is O(N)
The reason why merge sort can reduce the time complexity to O(NlogN) is that it does not waste the comparison process. Each comparison will be passed to the next merge. The sorting of O(N^2) wastes N comparison opportunities to get a number, and wastes a lot of comparison times.
Application of merge sort:
Example 1. Small sum problem: the sum of numbers smaller than it on the left of the number at each position in an array is called small sum. Find the sum of these small sums
public static int smallSum(int[] arr){
if(arr == null || arr.length<2){
return 0;
}
return mergeSort2(arr, 0, arr.length-1);
}
public static int mergeSort2(int arr[], int front, int end){
if(front == end){
return 0;
}
int mid = front + ((end - front)>>1);
return mergeSort2(arr, front, mid) + mergeSort2(arr, mid + 1, end) + merge2(arr,front, mid, end);
}
public static int merge2(int[] arr, int front,int mid, int end){
int[] help = new int[end - front + 1];
int p = front;
int q = mid + 1;
int i = 0;
int sum = 0;
while (p <= mid && q <= end){
if (arr[p] < arr[q]){
sum += arr[p] * (end - q + 1);
help[i++] = arr[p++];
}else {
help[i++] = arr[q++];
}
}
while (p <= mid){
help[i++] = arr[p++];
}
while (q <= end){
help[i++] = arr[q++];
}
for (i = 0; i < help.length; i++){
arr[front+i] = help[i];
}
return sum;
}
Example 2. Reverse order pair problem: if a number in an array is larger than the one on its right, this pair of numbers is called reverse order pair. Find all reverse order pairs, and the principle of small sum problem.
7, Quick sort
1. Dutch flag issue
1) Specify a num so that the number on the left of the array is less than or equal to num, and the number on the right of the array is greater than num. the time complexity O(N) and space complexity O(1) are required
Step: the pointer in the left area of the array starts with - 1. Traverse the traversal pointer from 0 to the right. If the number at this position is less than or equal to num, swap it with the number on the right of the left area, and add one to the pointer in the left area; If the number of this position is greater than num, continue to traverse down.
public static void partition1(int[] arr, int num){
int L = -1;
for (int i = 0; i < arr.length; i++){
if(arr[i] <= num){
swap2(arr, ++L, i);
}
}
}
2) Specify a num so that the number on the left of the array is less than num, the number in the middle of the array is equal to num, and the number on the right of the array is greater than num. the time complexity O(N) and space complexity O(1) are required
1.0 less than and equal to zone movement:
public static void partition2(int[] arr, int num){
int L = -1;
int M = -1;
for (int i = 0; i < arr.length; i++){
if(arr[i] < num){
swap2(arr, ++L, ++M);
swap2(arr, L, i);
}else if(arr[i] == num){
swap2(arr, ++M, i);
}
}
}
2.0: less than zone and greater than zone
public static void partition2_2(int[] arr, int num){
int L = -1;
int R = arr.length;
int i = 0;
while (i<R){
if(arr[i] < num){
swap2(arr, ++L, i++);
}else if(arr[i] > num){
swap2(arr, --R, i);
}else {
i++;
}
}
}
2. Quick sorting algorithm
1.0: use the last bit of the array as the partition value num, so that the left side of the array is less than or equal to num, and the right side is greater than num (the last bit remains unchanged), then exchange the last bit with the first bit on the right, divide the array into left and right sides, and then use the last bit on both sides as the partition value recursive call, and finally arrange the order.
2.0: using the Dutch flag problem, put the number equal to the partition value in the middle, and then recursively call the arrays on both sides.
2.0 will be slightly faster than 1.0, but the time complexity of the two algorithms is O(N^2) and the space complexity is O(N), because when the array is already ordered, it is the worst case, and each recursion can only solve one number.
3.0: take a random number in the array, exchange it with the number at the end of the array, and then use this number as the partition value for partition, so that all cases are equal probability events. Find an expectation for these probability events. Finally, the time complexity of the algorithm is O(NlogN) and the space complexity is O(logN)
public static void quickSort(int[] arr, int front, int end){
if(end > front){
swap2(arr, front + (int)(Math.random()*(end - front +1)), end);
int[] a = partition(arr, front, end);
quickSort(arr, 0, a[0]);
quickSort(arr, a[1], end);
}
}
public static int[] partition(int[] arr, int front, int end){
int L = front - 1;
int R = end;
int i = front;
while (i<R){
if(arr[i] < arr[end]){
swap2(arr, ++L, i++);
}else if(arr[i] > arr[end]){
swap2(arr, --R, i);
}else {
i++;
}
}
swap2(arr, end, R);
return new int[]{L, R+1};
}
8, Heap and heap sorting
1. Complete binary tree: a binary tree filled from left to right is called a complete binary tree
2. Large root pile and small root pile
Large root heap: a complete binary tree in which all parent nodes are larger than child nodes is called a large root heap
Small root heap: a complete binary tree in which all parent nodes are smaller than child nodes is called a small root heap
3. Nature of heap
A continuous segment of an array starting from zero can be represented as a heap. The left child of node I is 2i+1, the right child is 2i+2, and the parent node is (i-1)/2.
4,heapinsert
An empty array or a large root heap, add a number to the array, and keep the array as a large root heap through heapinsert operation.
Step: compare the number of this location with the parent node. If it is greater than the parent node, exchange with the parent node until it is not greater than the parent node or to position 0. The time complexity is O(logN)
//Does the number of index positions need to be moved upward to maintain the large root heap state of the array
public static void heapInsert(int[] arr, int index) {
while(arr[index] > arr[(index-1)/2]) {
swap2(arr, index, (index-1)/2);
index = (index-1)/2;
}
}
5,heapify:
For a large root heap, it is required to take its maximum value (i.e. the number at position 0) out of the heap, and the remaining number remains in the large root heap.
Step: copy the number of the last bit of the array to position 0, and then compare it with the maximum value of the left and right children. If it is smaller than the child, exchange it with the child until it is not smaller than the child or there is no child. The time complexity is O(logN)
//Start from the index position and go down to heapify
public static void heapIfy(int[] arr, int index, int heapsize) {
int left = 2*index+1;
//When I had children
while(left < heapsize) {
//Which is the older child, the left child or the right child
int largest = left + 1 < heapsize && arr[left] < arr[left+1] ? left+1 : left;
//Which is the older parent node and the largest child
largest = arr[largest] < arr[index] ? index : largest;
if(largest == index) {
break;
}
swap2(arr, largest, index);
index = largest;
left = 2*index+1;
}
}
If you change the value of a certain position in a large root heap array, you only need to heapinsert the number of that position up and heapify it down to keep the array in the large root heap structure.
6. Heap sort:
Steps: the initial heapsize is 0, then heapinsert one by one, heapsize + +, change the array into a large root heap, and then exchange the numbers at the beginning and end of the array. Heapsize –, do heapify, change the array into a large root heap, and then cycle heapify until the heapsize is 0. Time complexity O(NlogN), additional space complexity O(1)
//Heap sort
public static void heapSort(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
int heapsize = 0;
//O(N)
while(heapsize < arr.length) {
//O(logN)
heapInsert(arr, heapsize++);
}
//O(N)
while(heapsize > 0) {
O(1)
swap2(arr, 0, --heapsize);
//O(logN)
heapIfy(arr, 0, heapsize);
}
}
Faster method:
The heapingsert step is replaced by heapify, that is, the entire array is turned into a large root heap at one time by calling heapify successively from the lowest node. The time complexity of this method is O(N), which is better than O(logN) of heapinsert
After improvement:
public static void heapSort2(int[] arr) {
if(arr == null || arr.length < 2) {
return;
}
for(int i = arr.length-1; i>=0;i--) {
heapIfy(arr, i, arr.length);
}
int heapsize = arr.length;
//O(N)
while(heapsize > 0) {
O(1)
swap2(arr, 0, --heapsize);
//O(logN)
heapIfy(arr, 0, heapsize);
}
}
7. Extended questions:
An array is almost ordered, which means that the number in the array moves no more than k from disorder to order. k is a small number relative to the length of the array. Sort the array with the minimum time complexity.
*Note:
1. Capacity expansion: when adding numbers to the small root heap, each capacity expansion of the small root heap is multiplied. The cost of adding n numbers is O(N (maximum N copies) logN (maximum capacity expansion logN)), and the average cost of each number is O(logN)
2. The difference between the built-in heap and the handwritten heap: the built-in heap is actually a black box, and we can only interact with it through the add and poll functions. However, when there are other requirements (such as changing the number of a bit in the heap to keep it as a heap), the adjustment efficiency of the built-in heap is not as good as the handwritten heap, so we need to use the handwritten heap
Step: prepare a small root heap (in java, the bottom implementation of the priority queue is a small root heap). Add the first k+1 numbers in the front array to the small root heap. Since the number moves no more than k, there must be a minimum value in the first k+1 numbers. Therefore, pop up the number at the top of the heap in the small root heap at position 0, then add the number at position k+2 to the small root heap, and the number at the top of the heap continues to pop up is The number of 1 positions is looped to the end of the array, and the time complexity is O(Nlogk).
9, Comparator
Sort according to different standards.
The comparator rule consists of two parameters A and B. If A wants to be in the front, it returns A negative number; if B wants to be in the front, it returns A positive number; if it doesn't matter who is in the front, it returns 0.
Application, you can change the priority queue to a large root heap, or specify a more complex comparison strategy
public static class NodeComparator implements Comparator<Node>{
@Override
public int compare(Node o1, Node o2) {
return o1.weight - o2.weight;
}
}
PriorityQueue<Node> nodesqueue = new PriorityQueue<Node>(new EdgeComparator());
10, Non comparison sort
The previous sorting algorithms are based on comparison. The lower limit of theoretical time complexity is O(NlogN), while non comparison sorting is a special sorting algorithm that can be carried out according to data conditions, which can break through O(NlogN) to O(N).
1. Count sort
If the numbers in a group of data are in the j-k interval, we can prepare an array with the size of k-j+1, then traverse the array, record the occurrence times of j~k each number in the prepared array, and then restore the record array back to the original array to complete sorting. The time complexity is O(N+k-j), and the additional space complexity is O(k-j), However, this algorithm is only applicable when the k-j is small, otherwise the space cost will be very high.
2. Cardinality sort
Prepare ten buckets (queue) 0-9, put the numbers into the bucket according to the number of digits, then take out the bucket according to the first in first out principle, and then put the numbers into the bucket according to the number of ten digits, and so on. Cycle several times according to the number of digits of the largest number in the array, and finally finish the sorting.
11, Sort summary
1. Stability of sorting algorithm: the relative order of the same value remains unchanged after sorting.
The sorting stability of basic type data is useless, but it is useful for sorting complex type data such as objects.
| algorithm | Time complexity | Spatial complexity | stability |
|---|---|---|---|
| Select sort | O(N^2) | O(1) | instable |
| Bubble sorting | O(N^2) | O(1) | instable |
| Insert sort | O(N^2) | O(1) | stable |
| Merge sort | O(NlogN) | O(N) | stable |
| Quick sort (3.0) | O(NlogN) | O(logN) | instable |
| Heap sort | O(NlogN) | O(1) | instable |
| Bucket sorting | O(NlogN) | O(1) | instable |
| Bucket sort (count and cardinality sort) | stable |
The sorting algorithm gives priority to quick sorting, because the constant term of quick sorting is proved to be the smallest by experiments, so it is the fastest in theory; If space is required, heap sorting is preferred; If stability is required, merge sorting is preferred; According to the data status, bucket sorting can be considered.
Note:
1) Comparison based sorting with minimum time complexity O(NlogN)
2) Based on comparison, sorting algorithms with time complexity O(NlogN) and space complexity less than O(N) and stable do not exist at present.

The fifth point in the figure above is equivalent to fast sorting. It is the 01 standard partition. Its nature is the same as fast sorting. It is difficult to be stable.
2. Improvement of sequencing in Engineering
1) Make full use of the respective advantages of O(NlogN) and O(N^2) sorting. For example, when using insert sorting in small sample size (< = 60), you can take advantage of the small constant term of insert sorting, and when using quick sorting in large sample size, you can take advantage of the low time complexity of quick sorting. The same is true for merge sorting.
2) Stability considerations