48. Rotating image - medium - 9 / 26

48. Rotating image - medium - 9 / 26

Given an n × The two-dimensional matrix of N represents an image. Please rotate the image 90 degrees clockwise.

You have to rotate the image in place, which means you need to modify the input two-dimensional matrix directly. Do not use another matrix to rotate the image.

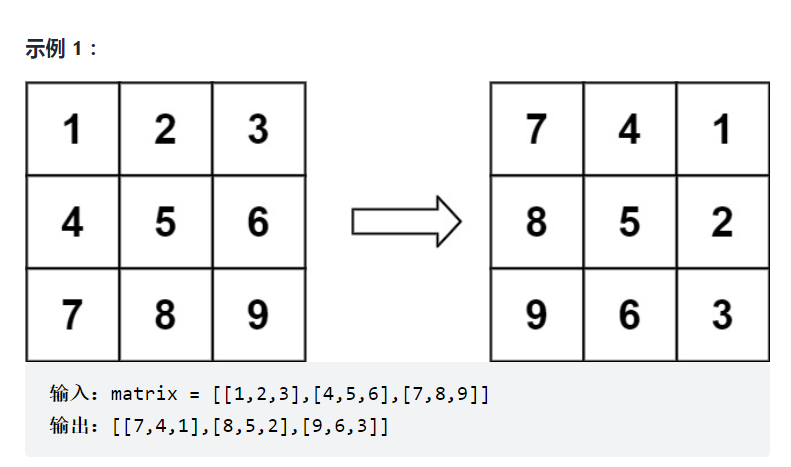
Analysis: find the law, first exchange according to the diagonal, and then exchange according to the axis of symmetry.

class Solution {
    public void rotate(int[][] matrix) {
        int l_len = matrix.length;

        //Diagonal exchange
        for(int i=0; i<l_len; i++){
            for(int j=0; j<=i; j++){
                if(i==j) continue; //Diagonal value, skip
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }

        //Symmetry axis exchange
        for(int i=0,j=l_len-1; i<l_len/2; i++,j--){
            for(int k=0; k<l_len; k++){
                int temp = matrix[k][i];
                matrix[k][i] = matrix[k][j];
                matrix[k][j] = temp;
            }
        }  
    
    }
}

Time complexity: O (n) ²).

Space complexity: O (1).

You can also exchange symmetrical rows with the transverse central axis as the axis, and then exchange them with diagonals.

49. Acronym grouping - medium - 9 / 27

49. Grouping of acronyms - medium

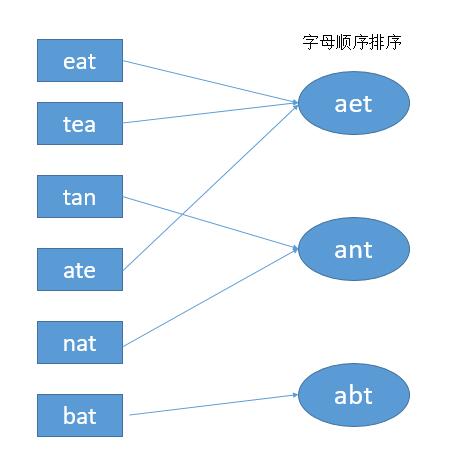
Give you a string array, please combine the letter ectopic words together. You can return the result list in any order.

An alphabetic ectopic word is a new word obtained by rearranging the letters of the source word. All the letters in the source word are used just once.

Parsing: sorting

Since the two strings of mutually alphabetic words contain the same letters, the strings obtained after sorting the two strings must be the same. Therefore, the sorted string can be used as the key of the hash table.

Form I:

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        //Create a HashMap store
        Map<String, List<String>> map = new HashMap<String, List<String>>();
        //ergodic
        for(String str: strs){
            //Convert string to character array
            char[] array = str.toCharArray();
            //sort
            Arrays.sort(array);
            //Save as key
            String key = new String(array);
            //When the key exists in the Map collection, the key value is used. If not, the default value defaultValue (the second parameter) is used
            List<String> list = map.getOrDefault(key, new ArrayList<String>());
            //Categorize the like and add them together
            list.add(str);
            //Add to map
            map.put(key, list);
        }
        //Returns all values in the map
        return new ArrayList<List<String>>(map.values());
    }
}

Form 2:

public List<List<String>> groupAnagrams(String[] strs) {
    HashMap<String, List<String>> hash = new HashMap<>();
    for (int i = 0; i < strs.length; i++) {
        char[] s_arr = strs[i].toCharArray();
        //sort
        Arrays.sort(s_arr);
        //Map to key
        String key = String.valueOf(s_arr); 
        //Add to the corresponding class
        if (hash.containsKey(key)) {
            hash.get(key).add(strs[i]);
        } else {
            List<String> temp = new ArrayList<String>();
            temp.add(strs[i]);
            hash.put(key, temp);
        }

    }
    return new ArrayList<List<String>>(hash.values()); 
}

Time complexity: O(nklogk), where n is the number of strings in strs and k is the maximum length of strings in strs. You need to traverse n strings. For each string, you need o (klogk) time to sort and O (1) time to update the hash table. Therefore, the total time complexity is O(nklogk).

Spatial complexity: O (nk), where n is the number of strings in strs and k is the maximum length of strings in strs. All strings need to be stored in a hash table.

53. Maximum subsequence sum - simple - 9 / 28

53. Maximum suborder sum - simple

Given an integer array nums, find a continuous sub array with the largest sum (the sub array contains at least one element) and return its maximum sum.

Analysis: dynamic programming

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        int dp = nums[0];
        int max = nums[0];
        for(int i=1; i < n; i++){
            //Take the larger value of the current accumulated number and the next number
            dp= Math.max(dp + nums[i],nums[i]);
            //Update maximum
            max = Math.max(max,dp);
        }
        return max;
    }
}

Time complexity: O (n), where n is the length of the num array. We only need to traverse the array once to find the answer.

Space complexity: O (1). We only need constant space to store several variables.

55. Jumping game - medium - 9 / 29

55. Jumping game - medium

Given a nonnegative integer array nums, you are initially at the first subscript of the array.

Each element in the array represents the maximum length you can jump at that position.

Judge whether you can reach the last subscript.

Resolution:

Each move takes the maximum number of jump steps (to get the maximum coverage). Each move of a unit updates the maximum coverage.

Local optimal solution of greedy algorithm: take the maximum number of jump steps each time (take the maximum coverage), and overall optimal solution: finally, get the overall maximum coverage to see whether it can reach the end point.

Local optimal launch global optimal, can not find a counterexample, try greed!

i can only move within the scope of cover every time i move. Each time i move an element, cover gets the supplement of the element value (new coverage) to let i continue to move.

The cover only takes Max each time (the range supplemented by the value of the element, the range of the cover itself).

If cover is greater than or equal to the end subscript, return true directly.

class Solution {
    public boolean canJump(int[] nums) {
        if(nums.length == 1) return true;
        //Coverage
        int coverRange = nums[0];
        //Update maximum coverage within coverage
        for(int i=0; i<=coverRange; i++){
            coverRange = Math.max(coverRange, i+nums[i]); //Update maximum coverage
            if(coverRange >= nums.length - 1){ //Returns true if the last one is overwritten
                return true;
            }
        }
        //If it is not overwritten, false is returned
        return false;
    }
}

56. Consolidation interval - medium - 9 / 30

56. Consolidation interval - medium

The array intervals is used to represent the set of several intervals, in which the single interval is intervals[i] = [starti, endi]. Please merge all overlapping intervals and return a non overlapping interval array, which needs to cover all intervals in the input exactly.

Resolution:

Use the left and right boundaries after the merged interval as a new interval and add it to the result array. If there is no merging, add the original interval to the result array.

class Solution {
    public int[][] merge(int[][] intervals) {
        List<int[]> res = new LinkedList<>(); //Store results
        //Sort by the first element of the array
        Arrays.sort(intervals, (o1,o2) -> Integer.compare(o1[0],o2[0]));
        //Define start
        int start = intervals[0][0];
        //ergodic
        for(int i=0; i<intervals.length-1; i++){
            //If the tail element of the current array is smaller than the head element of the next array, the current array is directly added into the array
            if(intervals[i][1] < intervals[i+1][0]){
                res.add(new int[]{start,intervals[i][1]});
                start = intervals[i+1][0]; //The update start position is the next array header element
            } else {
                //Update the tail element of the last array
                intervals[i+1][1] = Math.max(intervals[i+1][1],intervals[i][1]);
            }
        }
        res.add(new int[]{start,intervals[intervals.length-1][1]});
        return res.toArray(new int[res.size()][]);
    }
}