Joseph Ring

Joseph Ring was originally applied to the scenario of circular linked list. Because it takes time to build the circular linked list itself, we adopt a faster version of container instead

#include<iostream>
using namespace std;
#include<vector>
void JohnCircle(vector<int> arr, int m)
{
	int count = 1;
	auto it = arr.begin();
	while (arr.size() != 1)
	{
		if (count%m == 0)
		{
			cout << *it<< " ";
			it = arr.erase(it);
			it = it == arr.end() ? arr.begin() : it;
			count = 1;
		}
		else
		{
			count++;
			it = it == arr.end() - 1 ? arr.begin() : it + 1;
		}
	}

}

int main()
{
	vector<int> arr = { 1,2,3,4,5,6,7,8,9 };
	JohnCircle(arr, 3);
	system("pause");
}

The output result of the test case is:

3 6 9 4 8 5 2 7 Please press any key to continue. . .

Jump grid enhanced

The problem is similar to the previous grid that can only be down or up, except that it is a grid with m rows and n columns. You can jump from the upper left corner to the lower right corner, and then it is required that the number of times of skewing should not exceed k. how many routes are there from the upper left corner to the lower right corner?
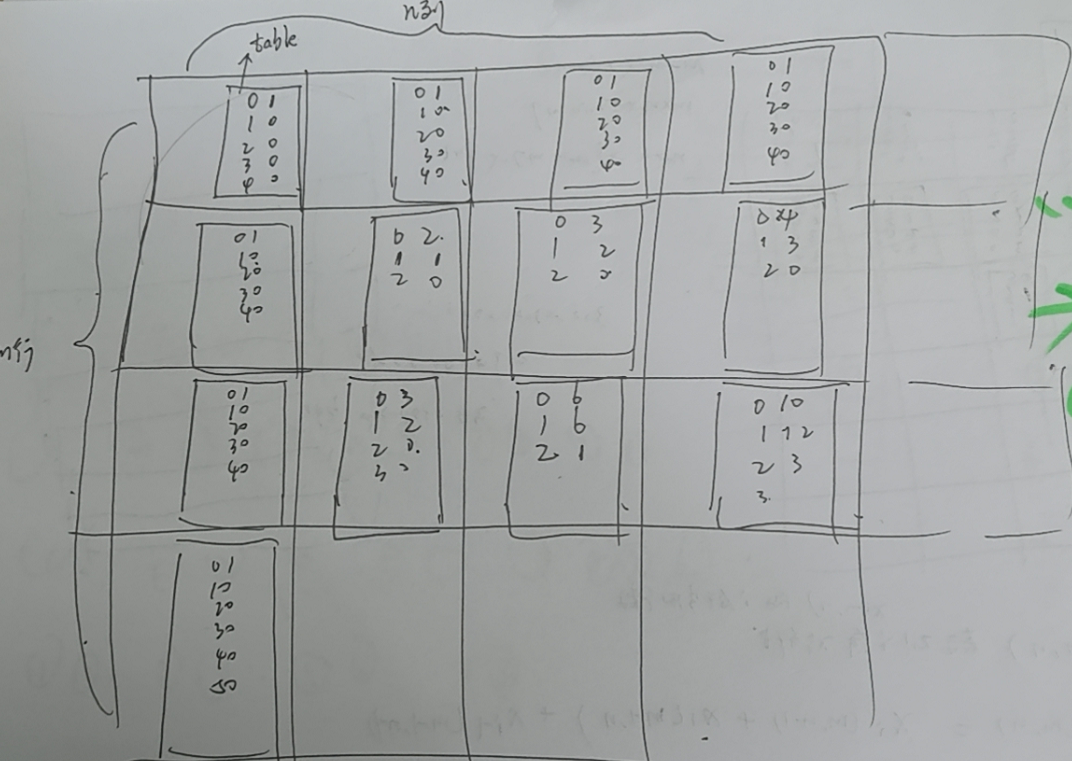
The idea is shown in the following figure:
Build a matrix of m*n, and maintain this table inside each element. The key of the table is the number of routes that need to go through value oblique jumps from the upper left corner to this position. The table length is min(n,m). The first row and the leftmost column use the default table
The default table is defined as
1 there is only one path without skew jump from the upper left point to this position, so all values are zero except the value of key=0 is 1
2. For the elements given by (m,n), assuming that there are x road stiffnesses with the number of oblique jumps i to this point, the following formula can exit the recurrence condition:

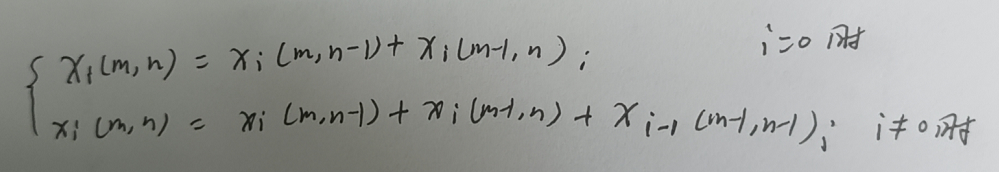
According to this recursive relationship, the state table of the nth element in row m can be obtained, and the value value of key < = k can be summed.

Idea: this question examines the idea of recursion and state transition, that is, you need to know where the route with oblique jump times i comes from among all the routes to element (m,n): (three sources)
1. Among all the routes to point (m-1,n), the route with oblique jump times i
2. Among all the routes to point (m,n-1), the route with oblique jump times i
3. Among all routes to (m-1,n-1), the route with oblique jump times of (i-1) (why is I-1 here)

The code is as follows:

#include<iostream>
#include<string>
using namespace std;
#include<vector>

//A grid that can jump sideways
int Min(int x, int y)
{
	return x < y ? x : y;
}

//Enter the grid with m rows and n columns. It is required that the number of oblique jumps can be greater than k times
int test(int m, int n, int k)
{
	vector<vector<int>>  pre_row;
	
	//If m=4,n=4, the table factory is 4
	vector<int> defalt_table;
	int table_length = Min(m, n);
	for (int i = 0; i < table_length; i++)
	{
		if (i == 0)
		{
			defalt_table.push_back(1);
		}
		else
		{
			defalt_table.push_back(0);
		}
	}
	//The previous is used to generate the default table

	//Place the default table in each element of the forward table
	for (int i = 0; i < n; i++)
	{
		pre_row.push_back(defalt_table);
	}
	

	vector<vector<int>>  current_row;

	for (int row = 0; row < m-1; row++)
	{

	
	current_row.push_back(defalt_table);
	vector<int> new_table;
	new_table.resize(table_length);
	for (int col_index = 1; col_index < n; col_index++)
	{
		for (int i = 0; i < table_length; i++)
		{
			if (i == 0)
			{
				new_table[i] = pre_row[col_index][i] + current_row[col_index - 1][i];
			}
			else
			{
				new_table[i] = pre_row[col_index][i] + current_row[col_index - 1][i] + pre_row[col_index-1][i-1];
			} 

		}
		current_row.push_back(new_table);
	}
	//Here, current_row is generated

	pre_row = current_row;
	current_row.clear();
	}

	int sum = 0;
	int lcoa = 0;
	while (lcoa <= k)
	{
		sum += pre_row[n - 1][lcoa++];
	}
	return sum;

}






int main()
{
	int m, n, k;
	cin >> m >> n >> k;

	cout << test(m,n,k) << endl;
	system("pause");
	return 0;
}

Remove comment symbols from code

This topic can have multiple variants