JAVA algorithm review outline
sort
Select sort:
5,1,128,96,76,2
(1)1,5,128,96,76,2
(2)1,2,128,96,76,5
(3)1,2,5,96,78,128
(4)1,2,5,78,96,128
(5)1,2,5,78,96,128
Select Sorting: find the smallest element and insert it into the ordered area. There are no elements in the ordered area. Elements will be exchanged when inserting
programming
import java.util.Arrays;
public class xuanzepaixu {
public static void main(String[] args) {
int numbs[] = {5,1,128,96,76,2};
selectionSort(numbs);
System.out.println(Arrays.toString(numbs));
}
public static void selectionSort(int[] numbs){
for (int i = 0; i < numbs.length-1; i++) {
int min = i;
for (int j = i+1; j < numbs.length; j++) {
if (numbs[j]<numbs[min]){
min=j;
}
}
if (i!=min){
int tmp = numbs[i];
numbs[i]=numbs[min];
numbs[min]=tmp;
}
}
}
}
Insert sort
123,45,19,23,634,4
(1)45,123,19,23,634,4
(2)19,45,123,23,634,4
(3)19,23,45,123,634,4
(4)19,23,45,123,634,4
(5)4,19,23,45,123,634
Insert sort: insert sort, also known as direct insert sort. It is an effective algorithm for sorting a small number of elements. Insert sort is one of the simplest sort Method, its basic idea is to insert a record into the ordered table, so as to create a new ordered table with the number of records increased by 1. In its implementation process, a double-layer loop is used. The outer loop finds the position to be inserted in the ordered table in front of the current element for all elements except the first element, and moves it
programming
import java.util.Arrays;
public class Insert sort {
public static void main(String[] args) {
int numbs[] = {123,45,19,23,634,4};
InsertionSort(numbs);
System.out.println(Arrays.toString(numbs));
}
public static void InsertionSort(int[] numbs){
for (int i = 0; i < numbs.length-1; i++) {
for (int j = i+1; j > 0; j--) {
if (numbs[j]<numbs[j-1]){
int tmp = numbs[j];
numbs[j]=numbs[j-1];
numbs[j-1]=tmp;
}
}
}
}
}
Bubble sorting
5,1,128,96,76,2
(1) 1,5,96,76,2,128
(2) 1,5,76,2,96,128
(3) 1,5,2,76,96,128
(4) 1,2,5,76,96,128
(5) 1,2,5,76,96,128
It repeatedly visits the element column to be sorted and compares two adjacent elements in turn element , if the order (e.g. from large to small, from Z to A) is wrong, exchange them. The work of visiting elements is repeated until no adjacent elements need to be exchanged, that is, the element column has been sorted.
The name of this algorithm comes from the fact that the smaller elements will slowly "float" to the top of the sequence (in ascending or descending order) through exchange, just like in carbonated drinks carbon dioxide The bubble will eventually float to the top, so it is called "bubble sorting".
programming
import java.util.Arrays;
public class Bubble sorting {
public static void main(String[] args) {
int numbs[] = {1,5,96,76,2,128};
BubbleSort(numbs);
System.out.println(Arrays.toString(numbs));
}
public static void BubbleSort(int[] nums){
for (int i = 0; i < nums.length-1; i++) {
for (int j = 0; j < nums.length-1-i; j++) {
if (nums[j]>nums[j+1]){
int tmp = nums[j];
nums[j]=nums[j+1];
nums[j+1]=tmp;
}
}
}
}
}
Merge sort
Suppose there are 8 elements. In the first step, it is divided into four pairs, each pair of two elements is combined into four ordered sequences by merge algorithm; The second step is to divide the four sequences into two pairs and merge them into two ordered sequences by merge algorithm; Finally, merge algorithm is used to merge into an ordered sequence.
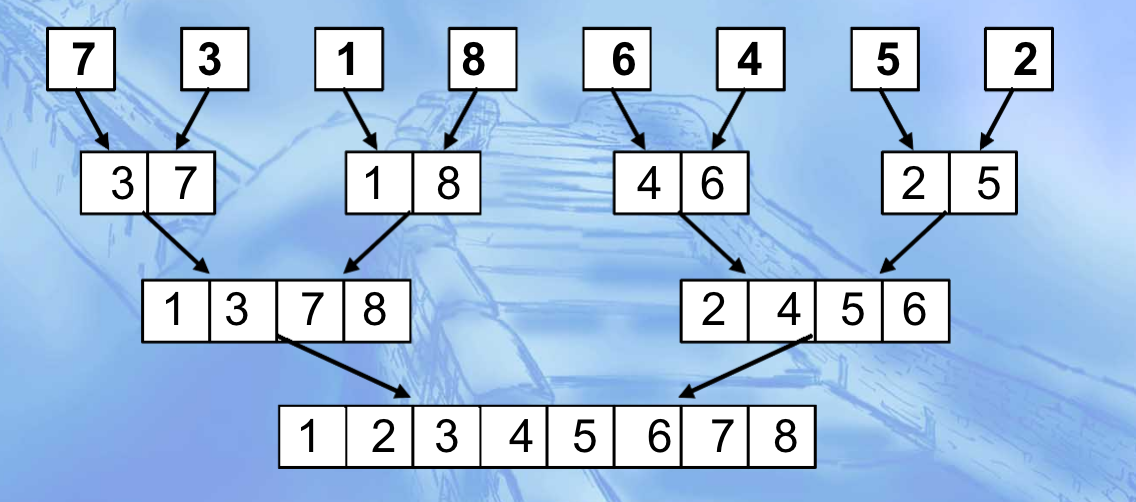
programming
Merge two ordered sequences and return the result
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Merge sort {
public static void main(String[] args) {
List<Integer> A = new ArrayList<Integer>();
A.add(1);
A.add(3);
A.add(7);
A.add(8);
List<Integer> B = new ArrayList<Integer>();
B.add(2);
B.add(4);
B.add(5);
B.add(6);
List<Integer> C = merge(A,B);
System.out.println(C);
}
public static List<Integer> merge(List<Integer> A, List<Integer> B){
List<Integer> C = new ArrayList<>();
int i=0;
int j=0;
int n = A.size();
int m = B.size();
while ((i<n)&&(j<m)){
if (A.get(i)<B.get(j)){
C.add(A.get(i));
i++;
}else{
C.add(B.get(j));
j++;
}
}
while (i<n){
C.add(A.get(i));
i++;
}
while (j<m){
C.add(B.get(j));
j++;
}
return C;
}
}
Heap build
4,1,6,3,8,2,10,5,9,11,7
[external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-z8324apz-1625552480498)( http://t4king.oss-cn-beijing.aliyuncs.com/uPic/%E5%A0%86%E5%BB%BA%E7%AB%8B (2)]. png)
Cardinality sort
Example: the keyword values of the elements in the linked list L are:
3097,3673,2985,1358,6138,9135,4782,1367,3684,0139
1. Distribute the elements in L to the linked list according to the number d1 in the keyword:
| L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 |
|---|---|---|---|---|---|---|---|---|---|
| 4782 | 3673 | 3684 | 2985 | 3097 | 1358 | 0139 | |||
| 9135 | 1367 | 6138 | |||||||
After linking the order of elements from l0 to L9 to L, the order of elements in L is as follows
4782 3673 3684 2985 9135 3097 1367 1358 6138 0139
2. Distribute the elements in L to the linked list according to the number d2 in the keyword:
| L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 |
|---|---|---|---|---|---|---|---|---|---|
| 9135 | 1358 | 1367 | 3673 | 4782 | 3097 | ||||
| 6138 | 3684 | ||||||||
| 0139 | 2985 |
After linking the order of elements from l0 to L9 to L, the order of elements in L is as follows
9135 6138 0139 1358 1367 3673 4782 3684 2985 3097
3. Distribute the elements in L to the linked list according to the number d3 in the keyword:
| L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 |
|---|---|---|---|---|---|---|---|---|---|
| 3097 | 9135 | 1358 | 3673 | 4782 | 2985 | ||||
| 6138 | 1367 | 3684 | |||||||
| 0139 |
After linking the order of elements from l0 to L9 to L, the order of elements in L is as follows
3097 9135 6138 0139 1358 1367 3673 3684 4782 2985
4. Distribute the elements in L to the linked list according to the number d4 in the keyword:
| L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 |
|---|---|---|---|---|---|---|---|---|---|
| 0139 | 1358 | 2985 | 3097 | 4782 | 6138 | 9135 | |||
| 1367 | 3673 | ||||||||
| 3684 |
After linking the order of elements from l0 to L9 to L, the order of elements in L is as follows
0139 1358 1367 2985 3097 3673 3684 4782 6138 9135
Union_Find operation
find(x): find the set of element X
union(x,y): merge the set of element X and element Y into one set
Union
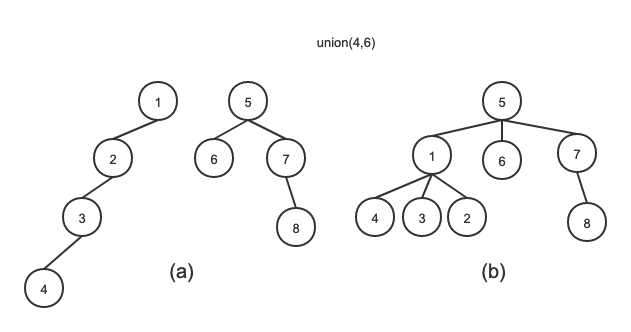
Use this data structure to merge two sets
Figure (a) shows the forest composed of sets {1,3,5,8}, {2,7,10}, {4,6}, {9}
Figure (b) shows the combination of the set of element 1 and the set of element 7
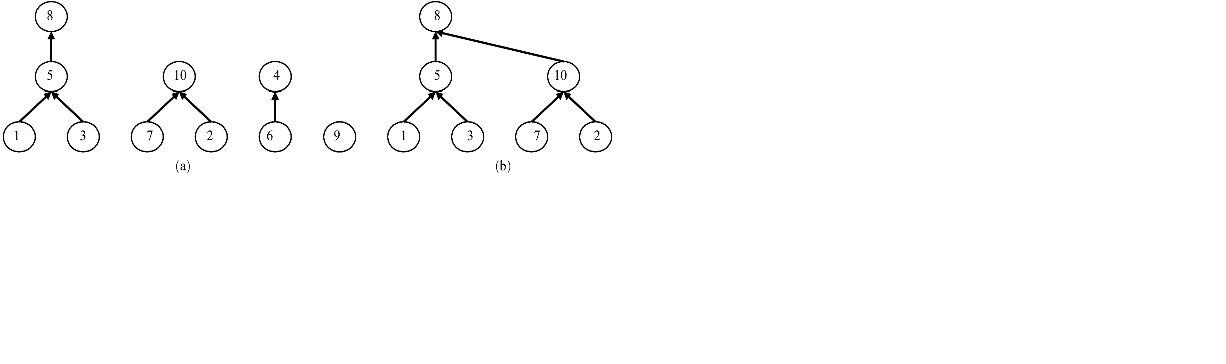
Disadvantages of this data structure
The height of the tree may be very large and become a degenerate tree and a linear table
union(x,y) operation:
If x and y are the root nodes of two different trees in the current forest,
If rank (x) > rank (y) takes x as the father of Y
If rank (x) < rank (y) takes y as the father of X
If rank(x) = rank(y) takes x as the father of Y, rank(x) + 1
Find
Path compression
During the find(x) operation, after finding the root node y of X, change the parent pointers of all nodes on the path along the path from X to y to make it directly point to y
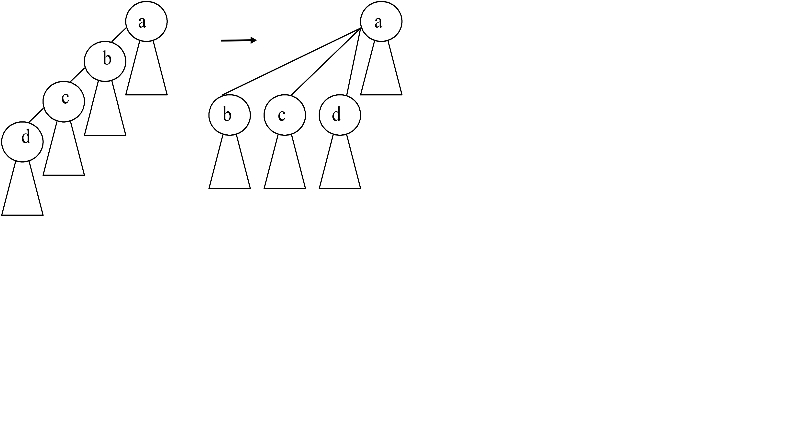
(a) Represents the set {1,2,3,4}, {5,6,7,8}
b) Indicates the result after executing union(4,6)
recursion
stratum
Calculate factorial function n!
Factorial function can be defined as
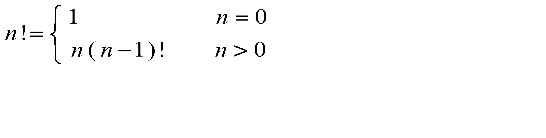
The recursive algorithm is as follows:
public class Recursive hierarchy {
public static void main(String[] args) {
int n =5;
System.out.println(f(n));
}
public static int f(int n){
if(n==0||n==1){
return 1;
}
return n*f(n-1);
}
}
Fibonacci sequence
Relation:
F(1)=F(2)=1;
F(n)=F(n-1)+F(n-2) (n≥3)
The recursive algorithm is as follows:
public class Fibonacci sequence {
public static void main(String[] args) {
int n = 20;
int f = f(n);
System.out.println(f);
}
public static int f(int n){
if (n==1||n==2){
return 1;
}
return f(n-1)+f(n-2);
}
}
Calculation of integer power
int power(int x,int n){
int y=0;
if(n==0)y==1;
else{
y=power(x,x/2);
y=y*y;
if(n%2==1)
y=y*x;
}
return y;
}
Recursion (2)
Array main element
A Yes n An array of elements, x yes A An element in, if A More than half of the elements in x The same is called x Is the main element of the array.
Example: array A={1,3,2,3,3,4,3},
Element 3 is the main element of the array
programming
public int getCandidate(int nums[], int begin, int end ){
int j = begin,count = 1;
int c = nums[j];
while(j<end-1 && count>0) {
j++;
if(nums[j]==c) {
count = count + 1;
}else {
count = count - 1;
}
}
if(j==end-1 && count>0) {
return nums[j]; //When the remaining time indicates that it is likely to be a group element, we return the subscript to the verification function for verification
}else if(j==end-1 && count == 0 ) {
return 0; //Returning 0 means there is no group element
}else {
return getCandidate(nums,j,end); //Recursive call
}
}
Divide and conquer
The process of solving the maximum and minimum problem by divide and conquer method
Example of the process of solving the maximum and minimum problem by divide and conquer method:
Divide and conquer algorithm for merge sort
Implementation of algorithm
merge_sort(Type A[ ], int low, int high)
{ int mid;
if (high > low)
{ mid = (high – low) / 2;
merge_sort(A[ ], low, mid);
merge_sort(A[ ], mid + 1, high);
merge(A[ ], low, mid, high, high – low);
}
}
Quick sort
The sequence is divided into two subsequences locally, so that all elements of the first subsequence are smaller than all elements of the second subsequence. This division is carried out continuously, and finally n subsequences are formed. Each subsequence has only one element. At this time, the whole sequence is a sequence sorted in incremental order
Pivot element:
Rearrange the sequence by taking the first element of the sequence as the pivot element
void quick_sort(Type A[ ], int low, int high)
{
int k;
if (low < high) {
k = split(A, low, high);
quick_sort(A, low, k-1);
quick_sort(A, k+1, high);
}
}
Quickly sort the following numbers:
8,1,4,9,0,3,5,2,7,6
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-82afxdov-162555280506)( http://t4king.oss-cn-beijing.aliyuncs.com/uPic/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F (1)]. png)
Linear selection
How many partitions are needed to find the third largest
137,96,88,108,17,87,65,35,76,45,66,18
(a)17,18,88,108,137,87,65,35,76,45,66,96
(b)88,66,45,87,65,35,76,96,108,137
How many partitions are needed to find the fifth small by the following number
8 1 4 9 0 3 5 2 7 6
(a) 2 1 4 5 0 3 6 9 2 7
(b) 2 1 0 3 4 5
© 4
Divide and conquer (2) selection problem
Median (group of 5 elements)
① If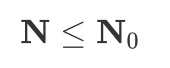 , directly sort the array, and the k-th element is the desired element; Otherwise, turn to ②
, directly sort the array, and the k-th element is the desired element; Otherwise, turn to ②
② The elements are divided into p = ⌊ n / 5 ⌋ groups with 5 elements in each group. The group with less than 5 elements will not be processed
③ Take the median elements of each group to form an array M with scale p
④ Recursively execute the algorithm on the array m to obtain a median element M with a median value
⑤ The original array is divided into three groups, so that elements greater than m are stored in P, elements equal to m are stored in Q, and elements less than m are stored in R
⑥ If | P | > k, the algorithm is executed recursively for p; Otherwise, turn to ⑦
⑦ If | P | + | Q | > k, m is the selected element; Otherwise, turn to 8;
⑧ The algorithm is executed recursively on Q.
Examples
Find the 16th largest element of the following 37 elements;
35, 43, 2, 19, 28, 62, 36, 7, 5, 13, 25, 13, 32, 11, 1, 9, 12, 23, 37, 39, 58, 43, 41, 51, 27, 8, 26, 34, 22, 15, 19, 54, 48, 30, 24, 6, 10

greedy algorithm
Continuously select the value of an optimal element from the n elements of the problem as a component of the local solution vector, so that it can not only meet the constraint equation, but also make the extreme value of the objective function the fastest. When the values of n elements are obtained, the solution vector becomes a complete vector, which is the solution of the problem
knapsack problem
Backpack with load capacity of M, weight of . the value is
. the value is Objects, 1 ≤ i ≤ n, fill the backpack with objects to maximize the value of objects in the backpack
Objects, 1 ≤ i ≤ n, fill the backpack with objects to maximize the value of objects in the backpack
The knapsack problem with separable objects and the knapsack problem with indivisible objects are called 0 / 1 knapsack problem
Knapsack problem (separable), n=7,m=20
Load value 12, 7, 5, 19, 20, 18, 13
Weights 4, 5, 3, 9, 10, 11, 18
| Load value | 12 | 7 | 5 | 19 | 20 | 18 | 13 |
|---|---|---|---|---|---|---|---|
| weight | 4 | 5 | 3 | 9 | 10 | 11 | 18 |
| / | / | / | / | / | / | / | / |
| Average value | 3 | 1.4 | 1.7 | 2.1 | 2 | 1.63 | 0.72 |
| ☑️ | ☑️ | ☑️ |
Maximum value: 12 + 19 + 2 * 7 = 45
Unit shortest path
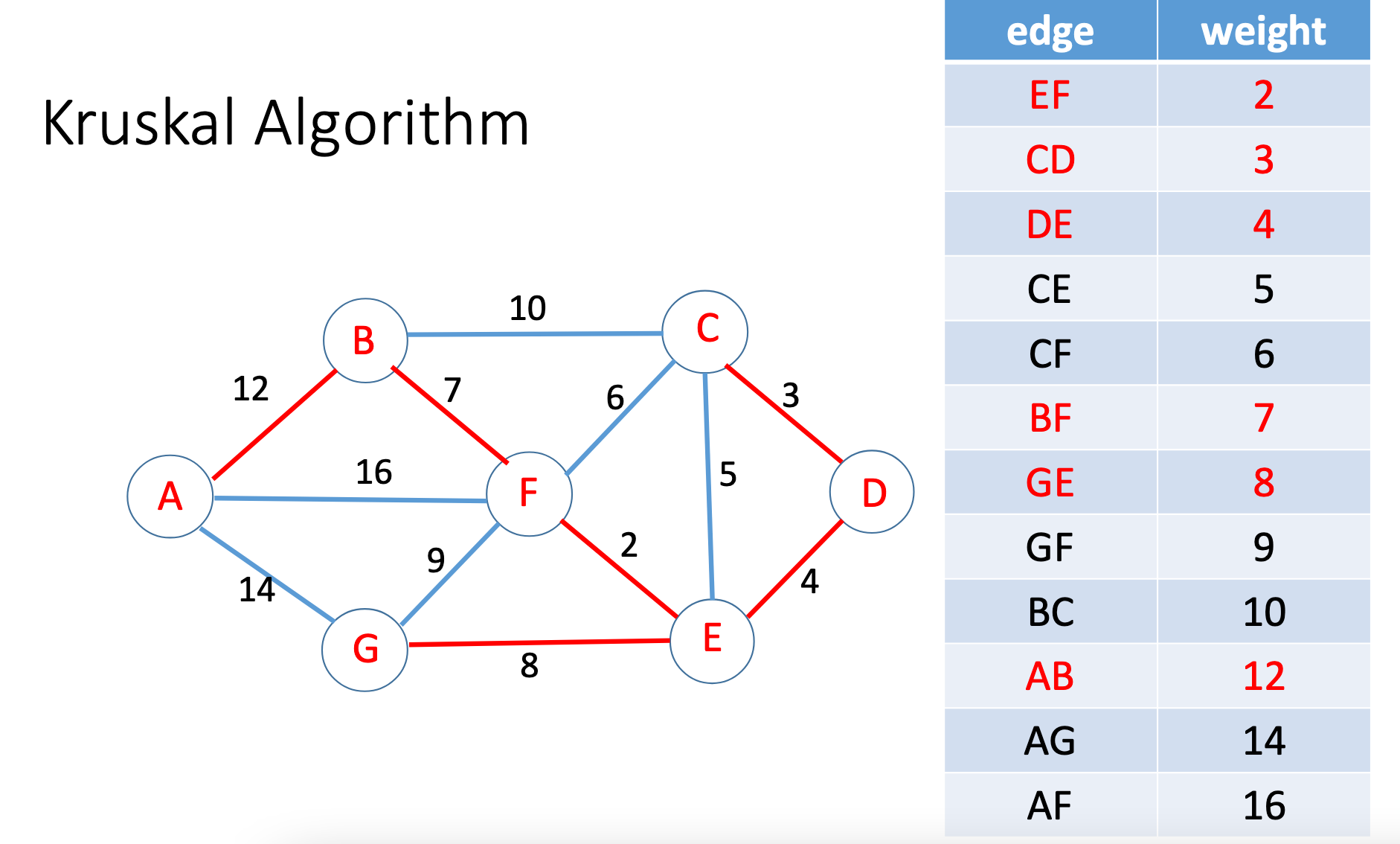
Dijkstra algorithm

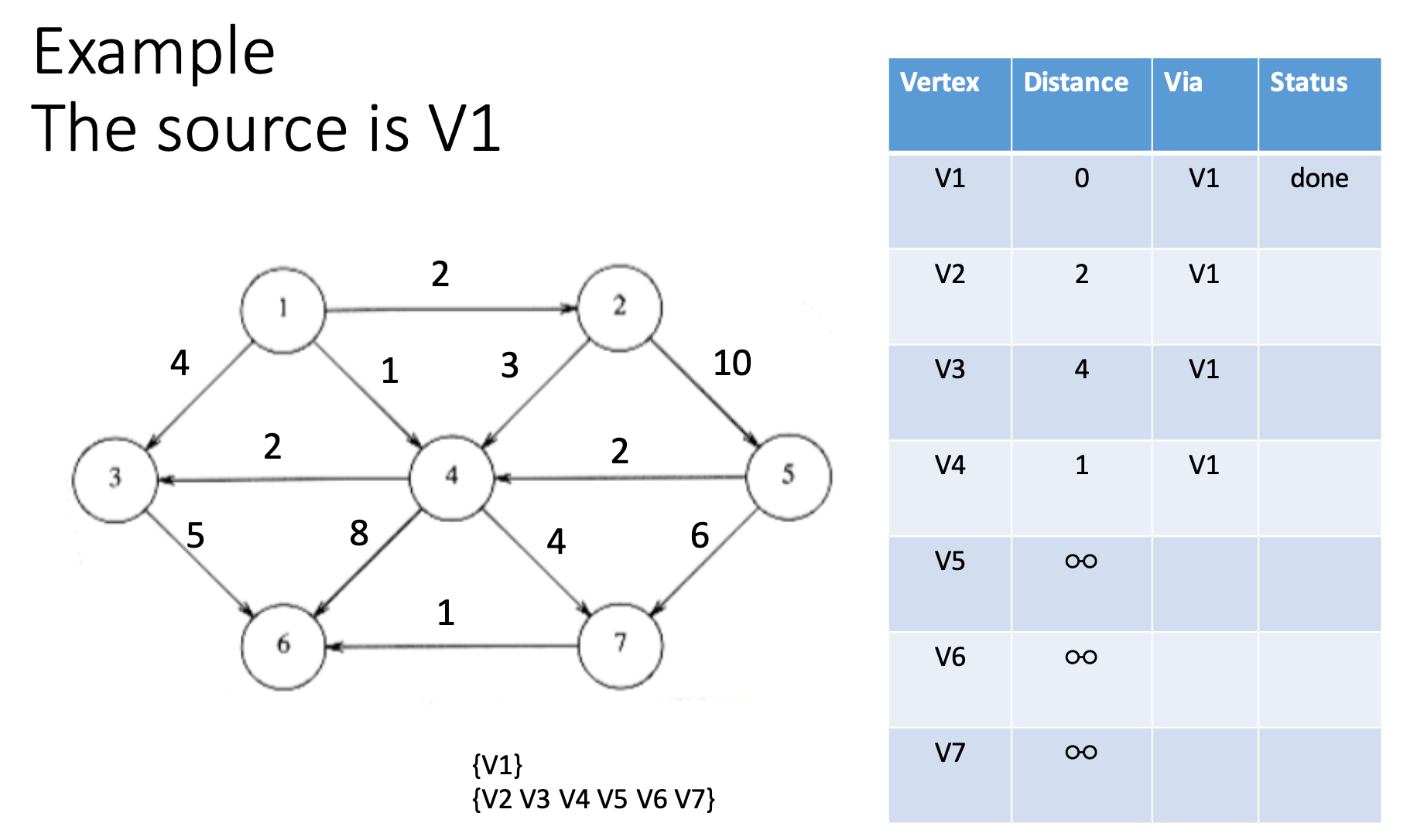
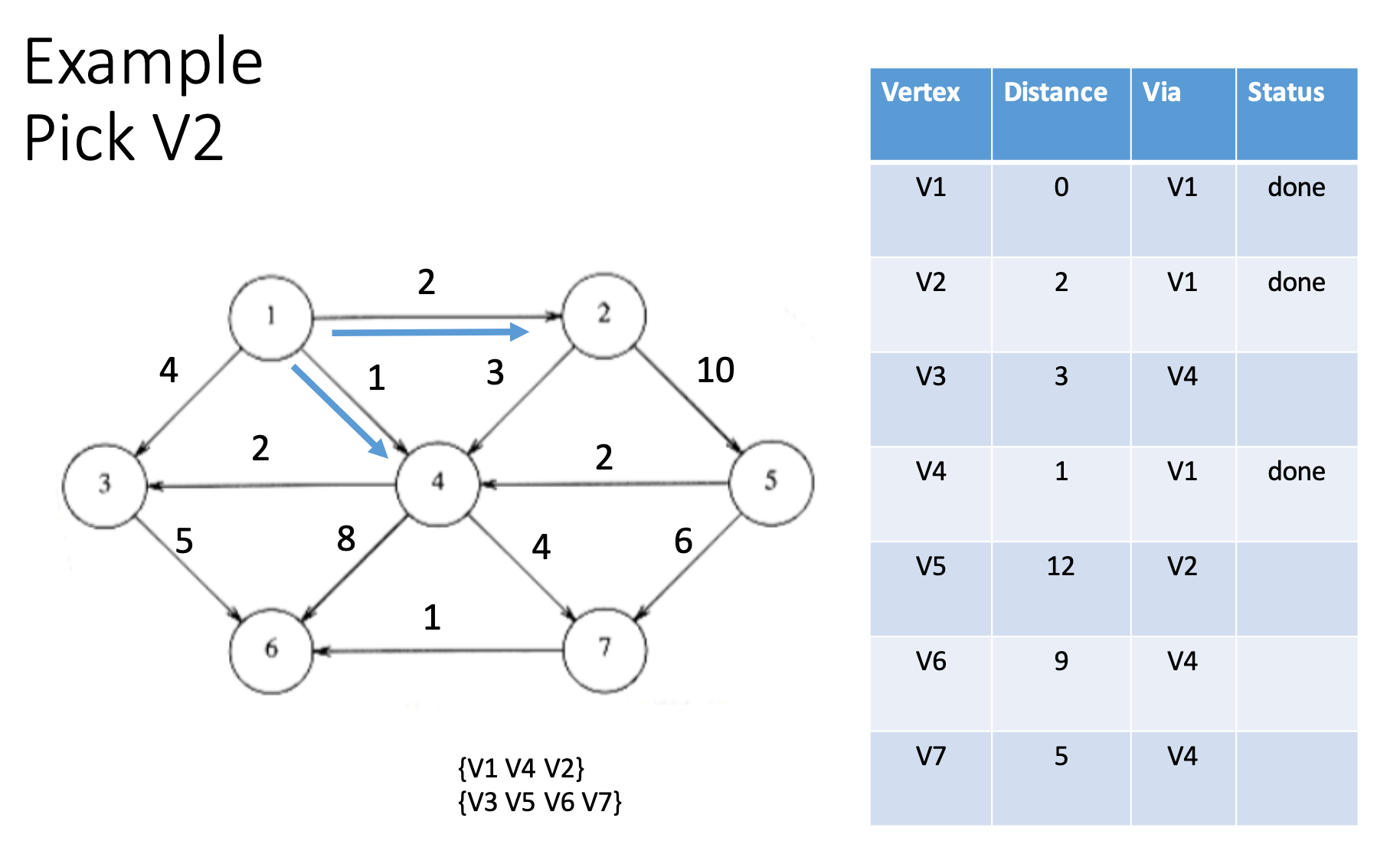
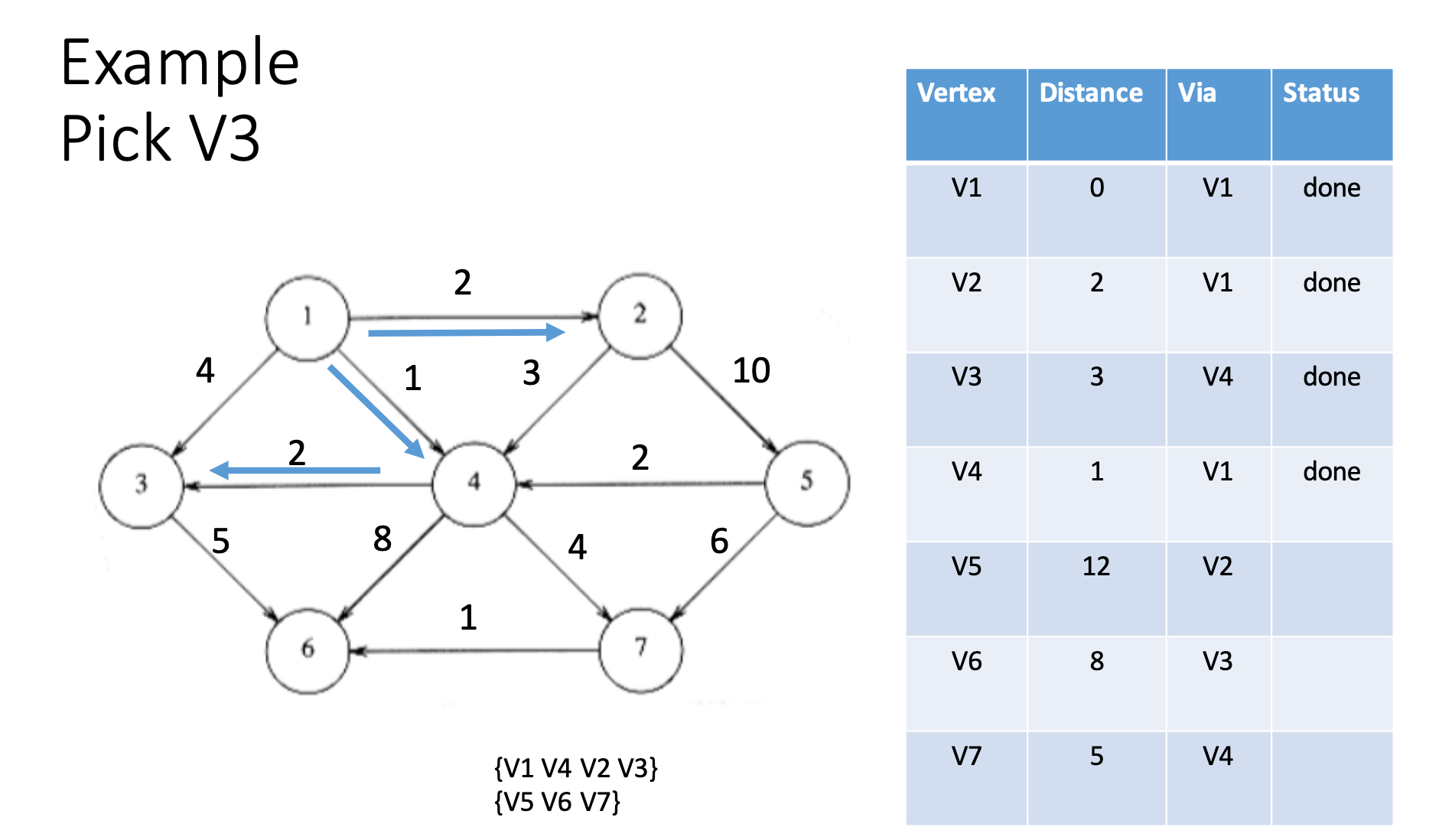
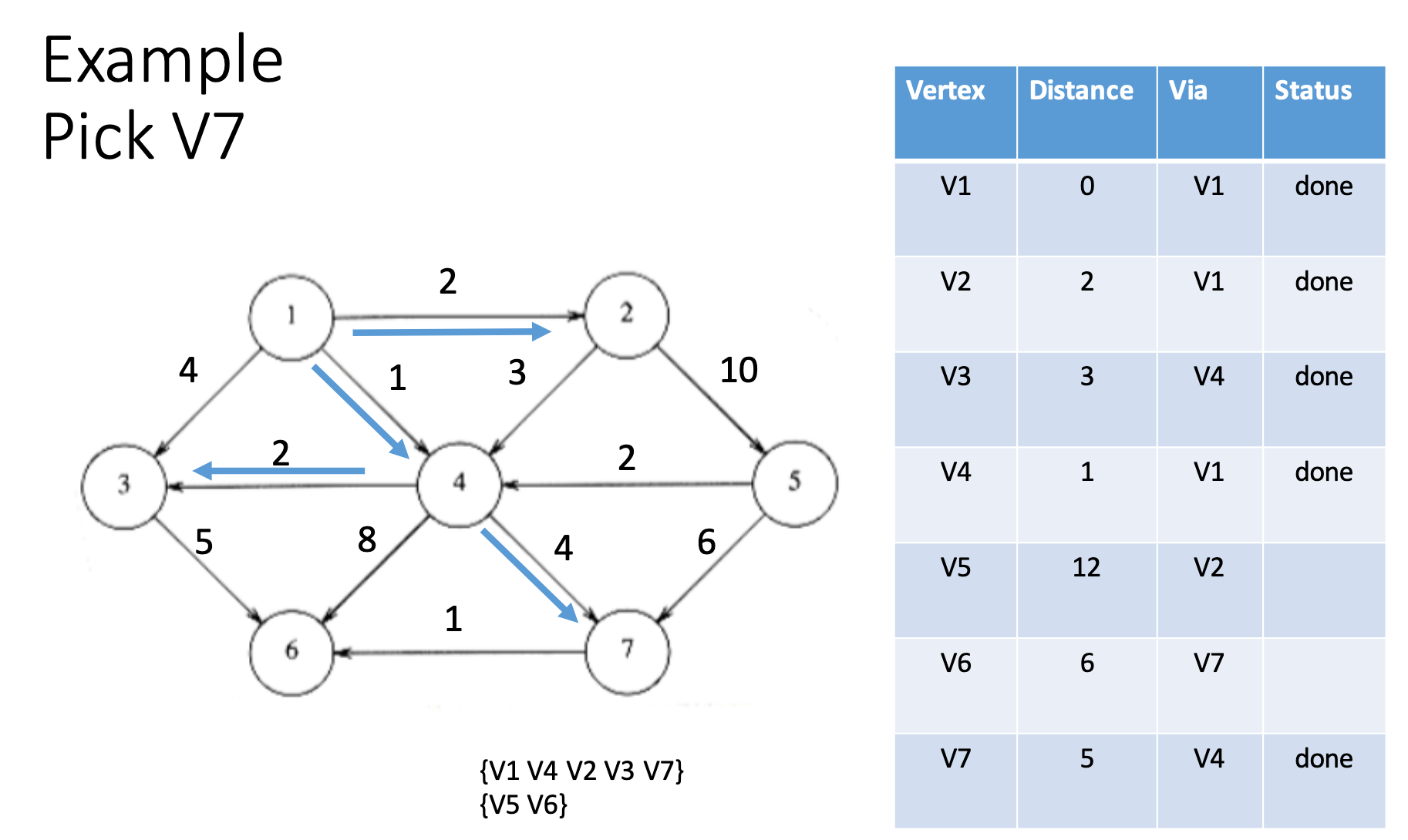
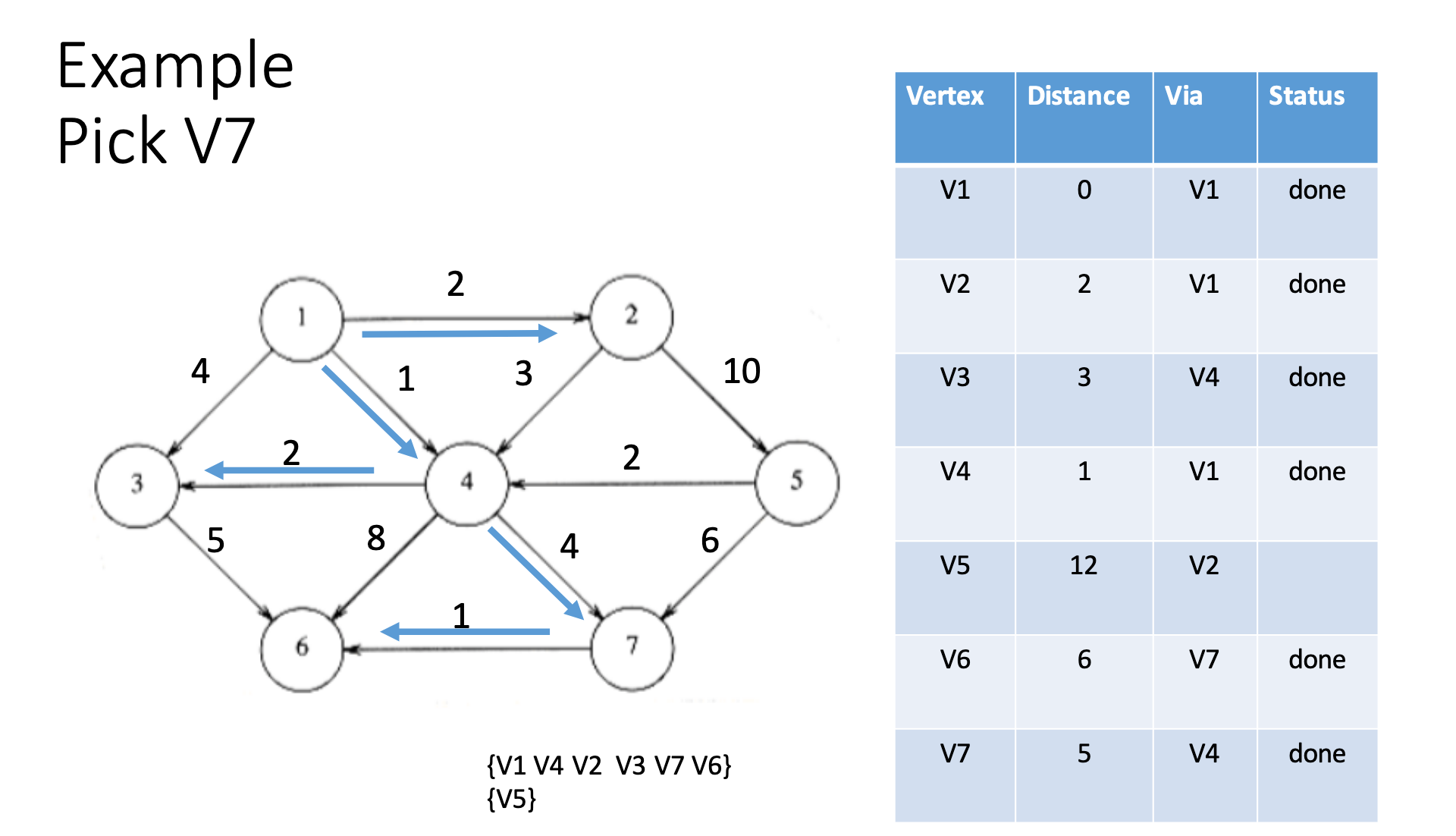

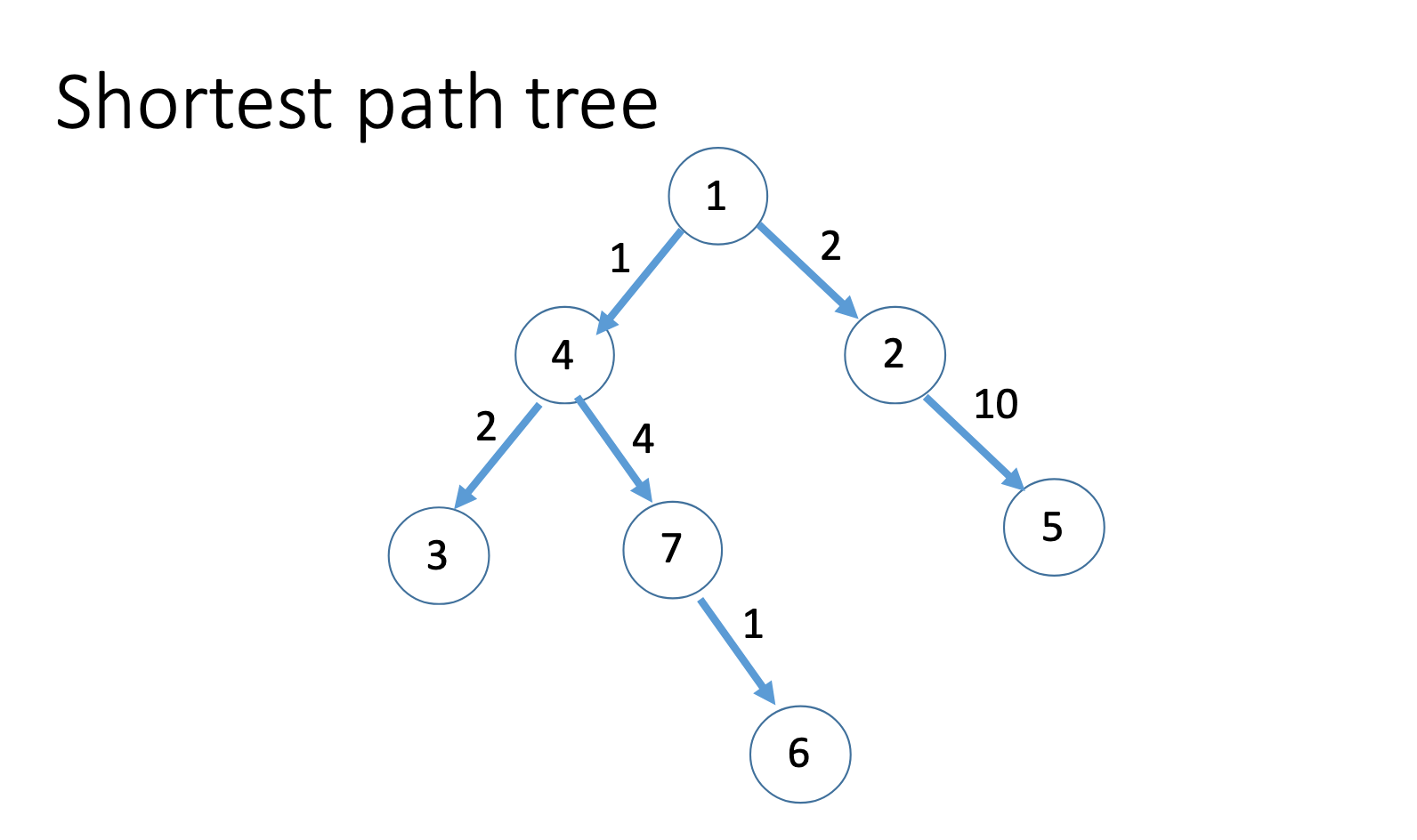
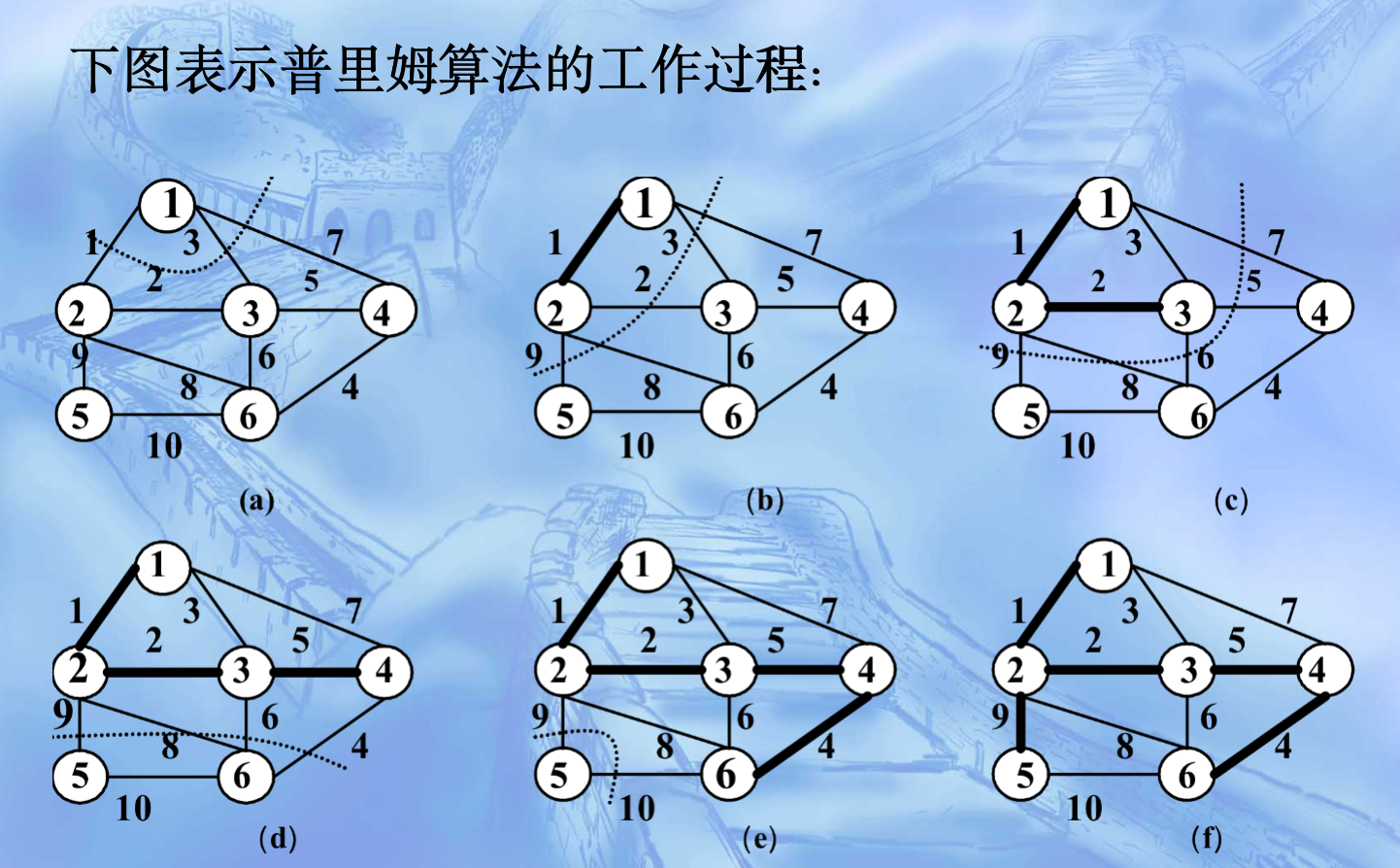
Prim
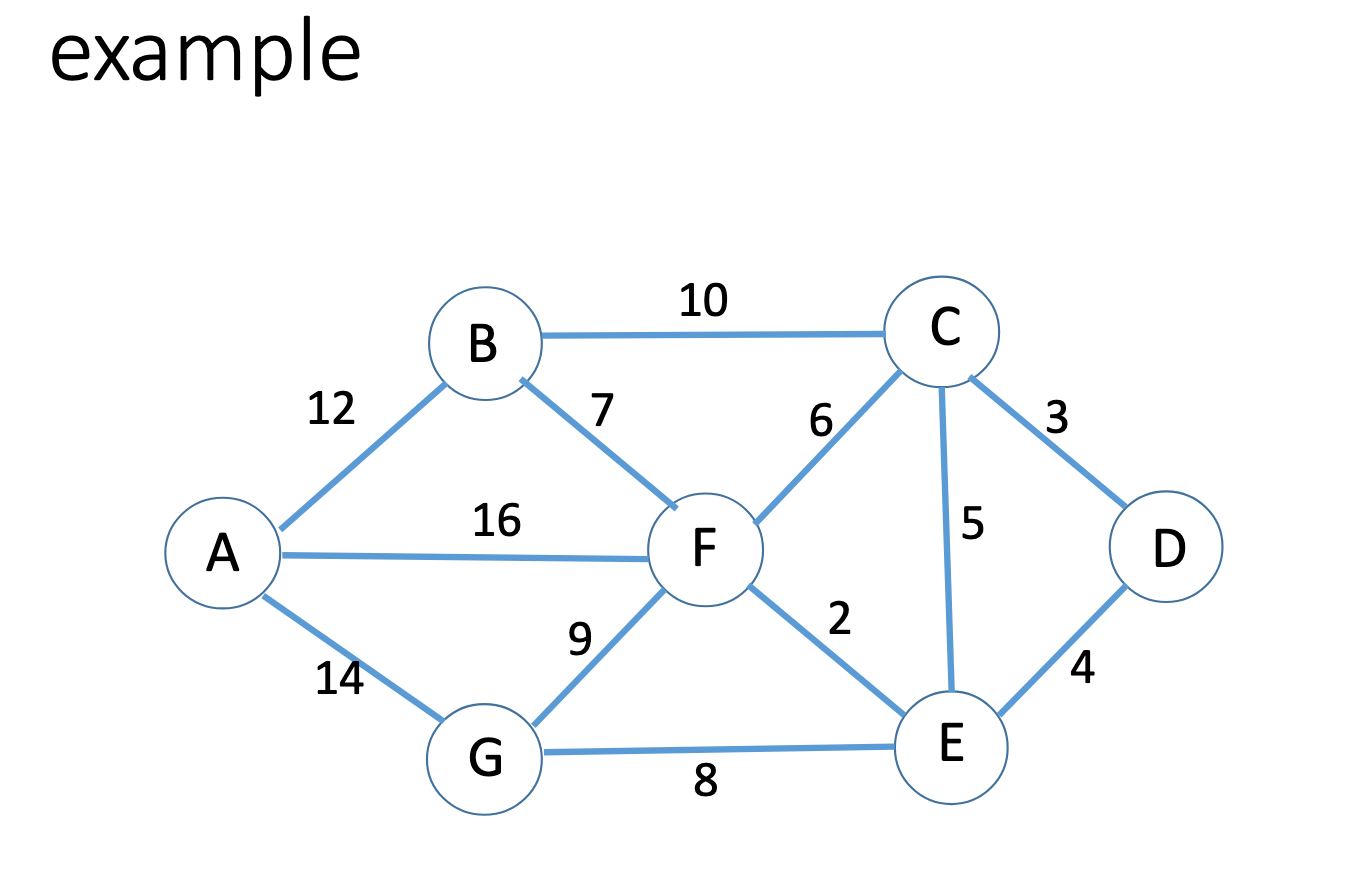
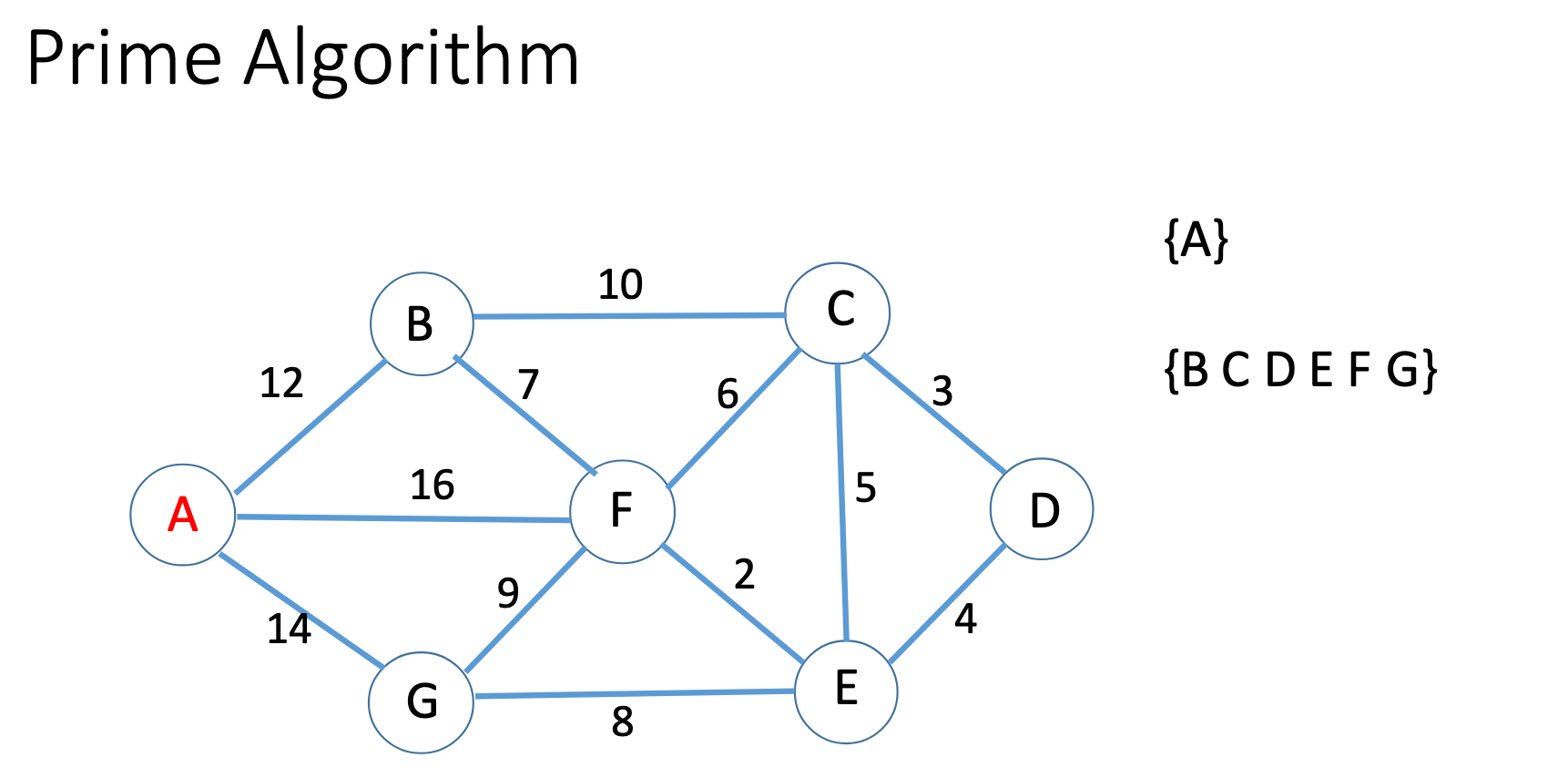
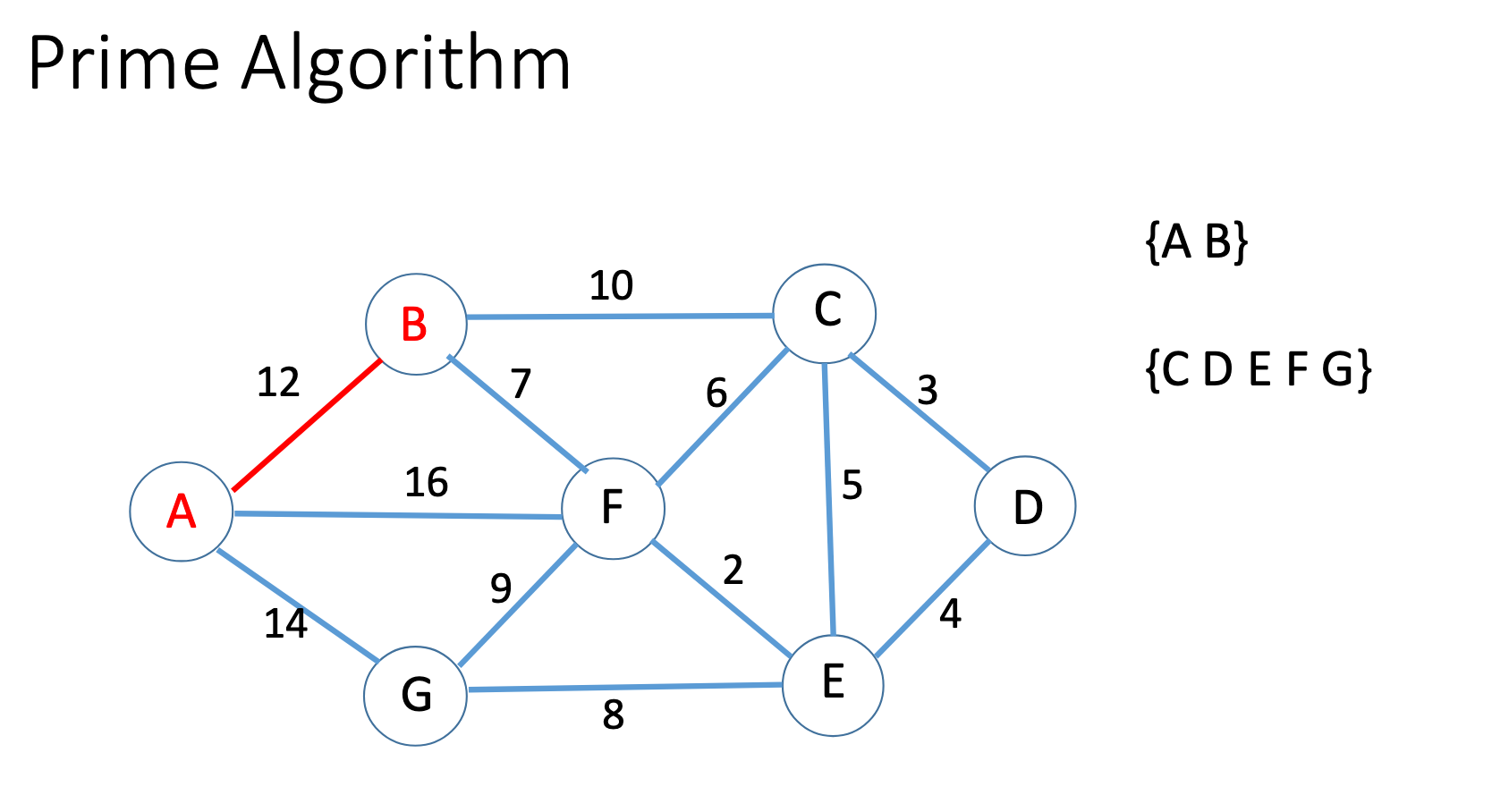
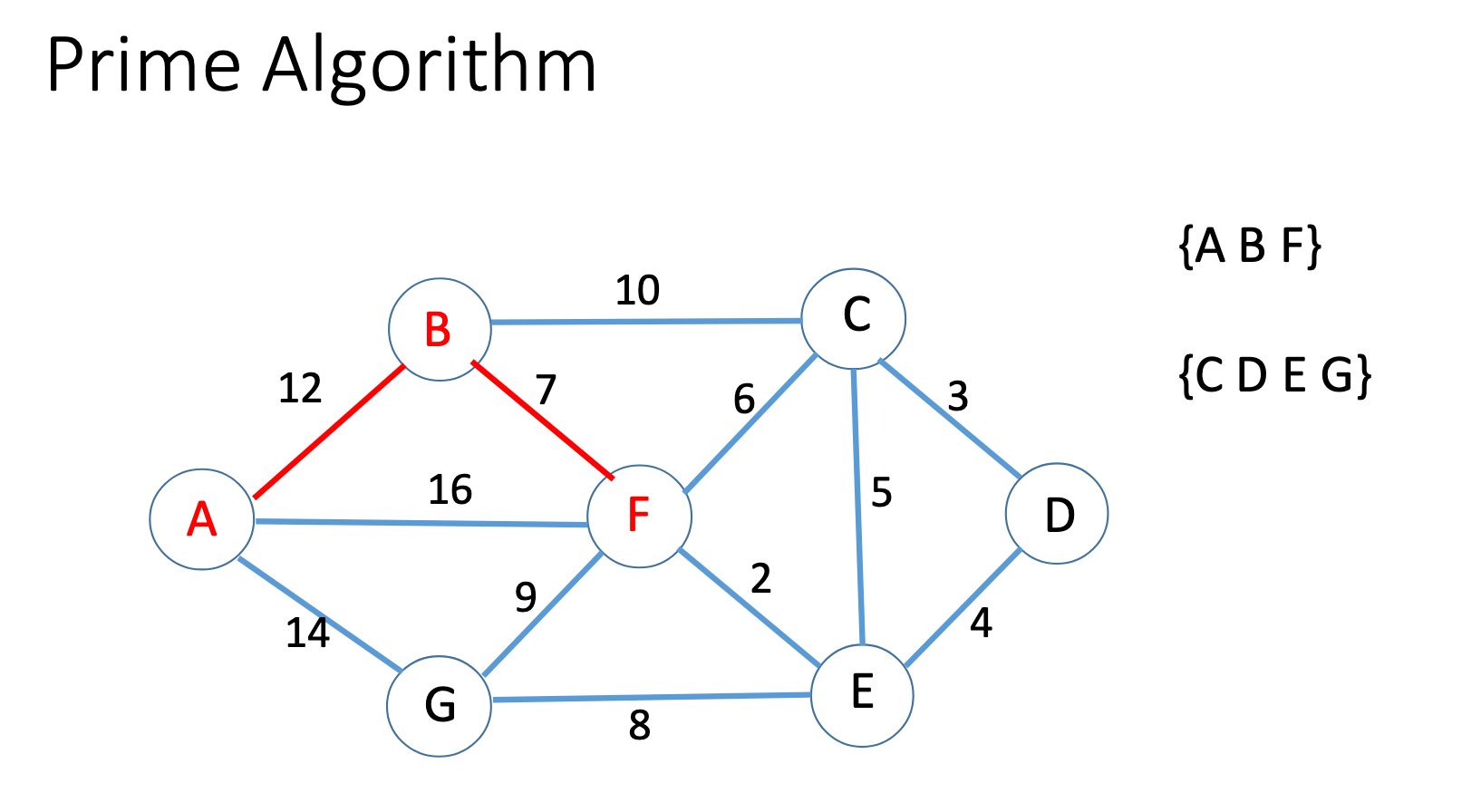
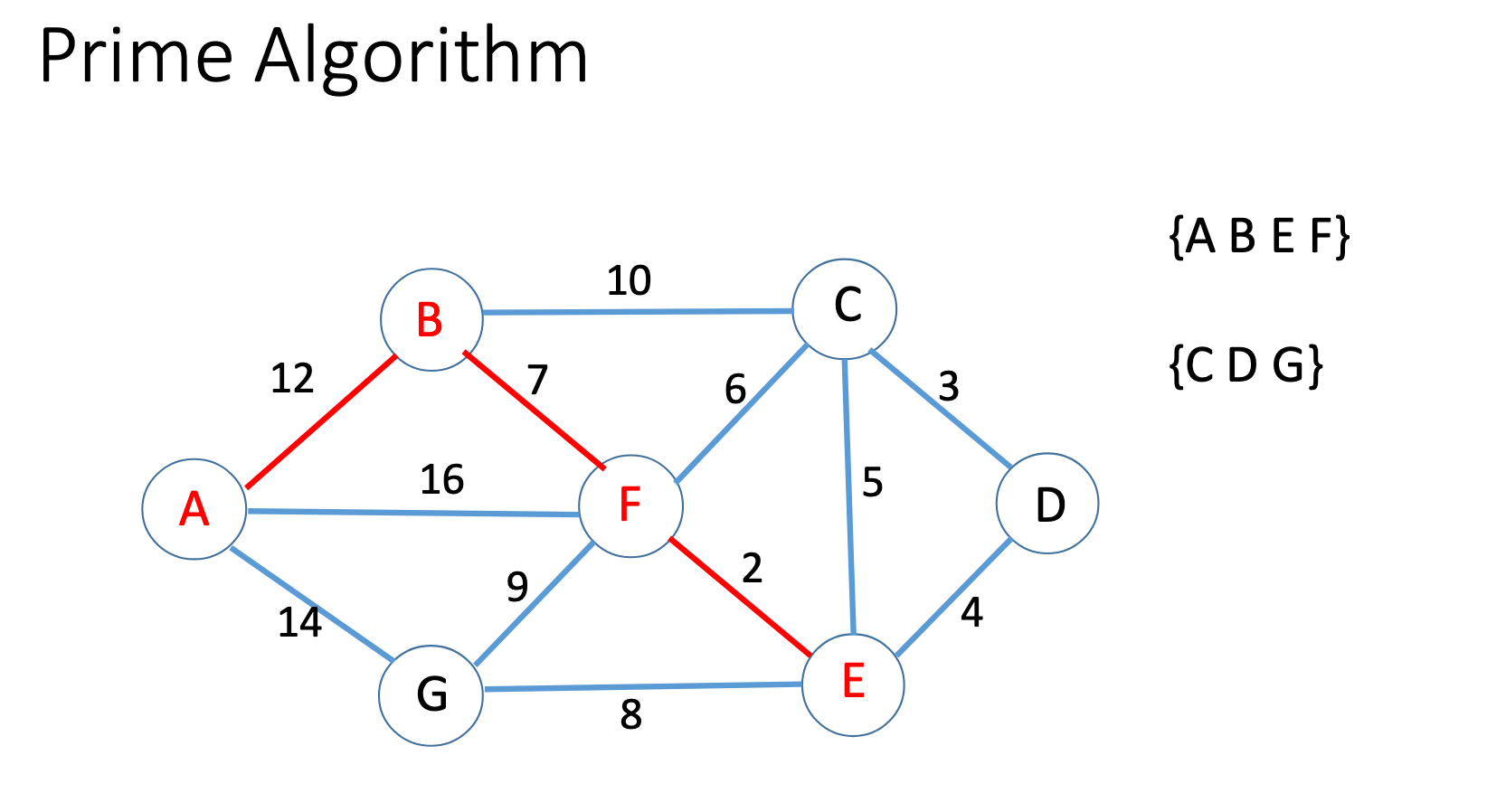
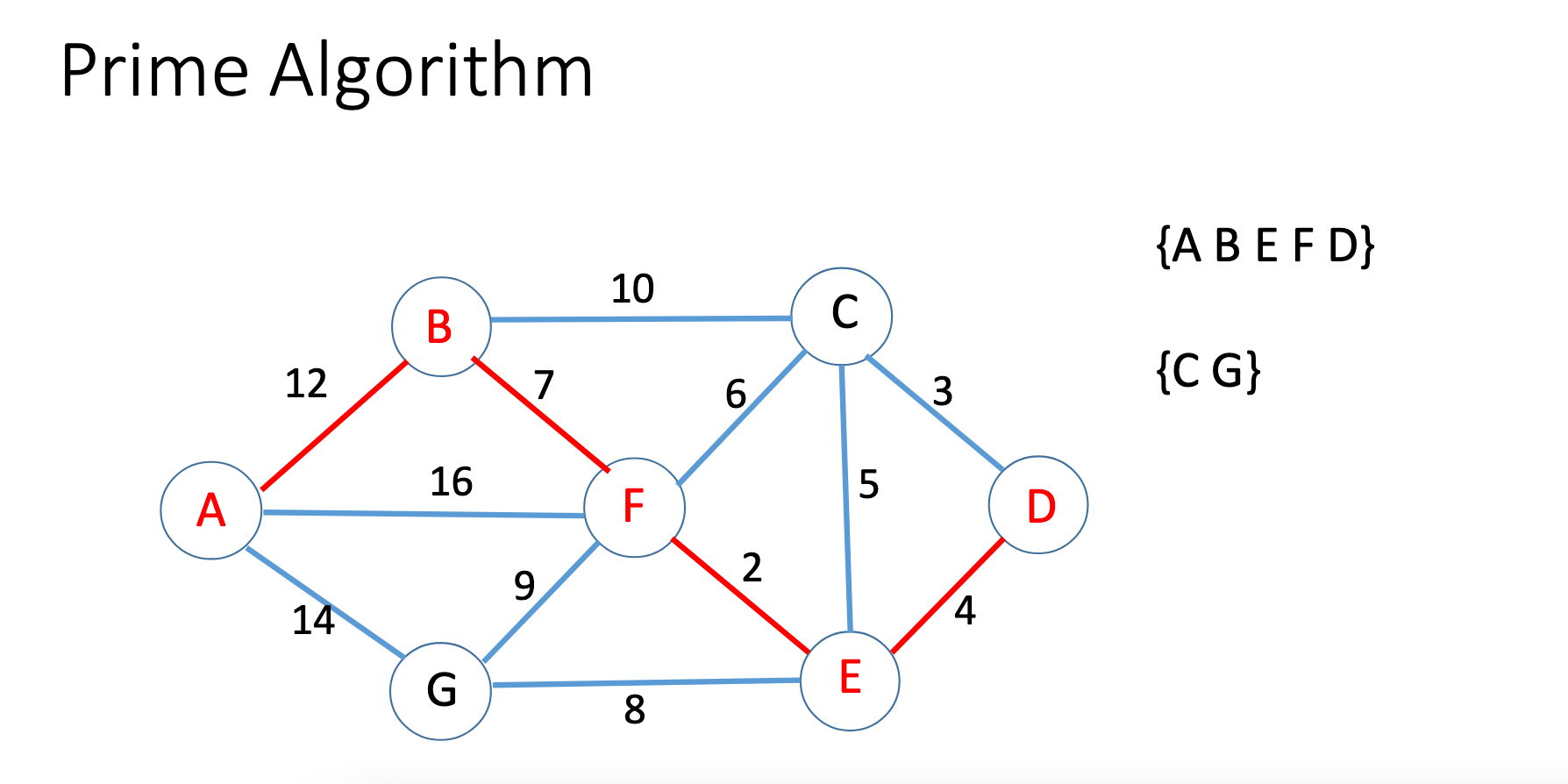
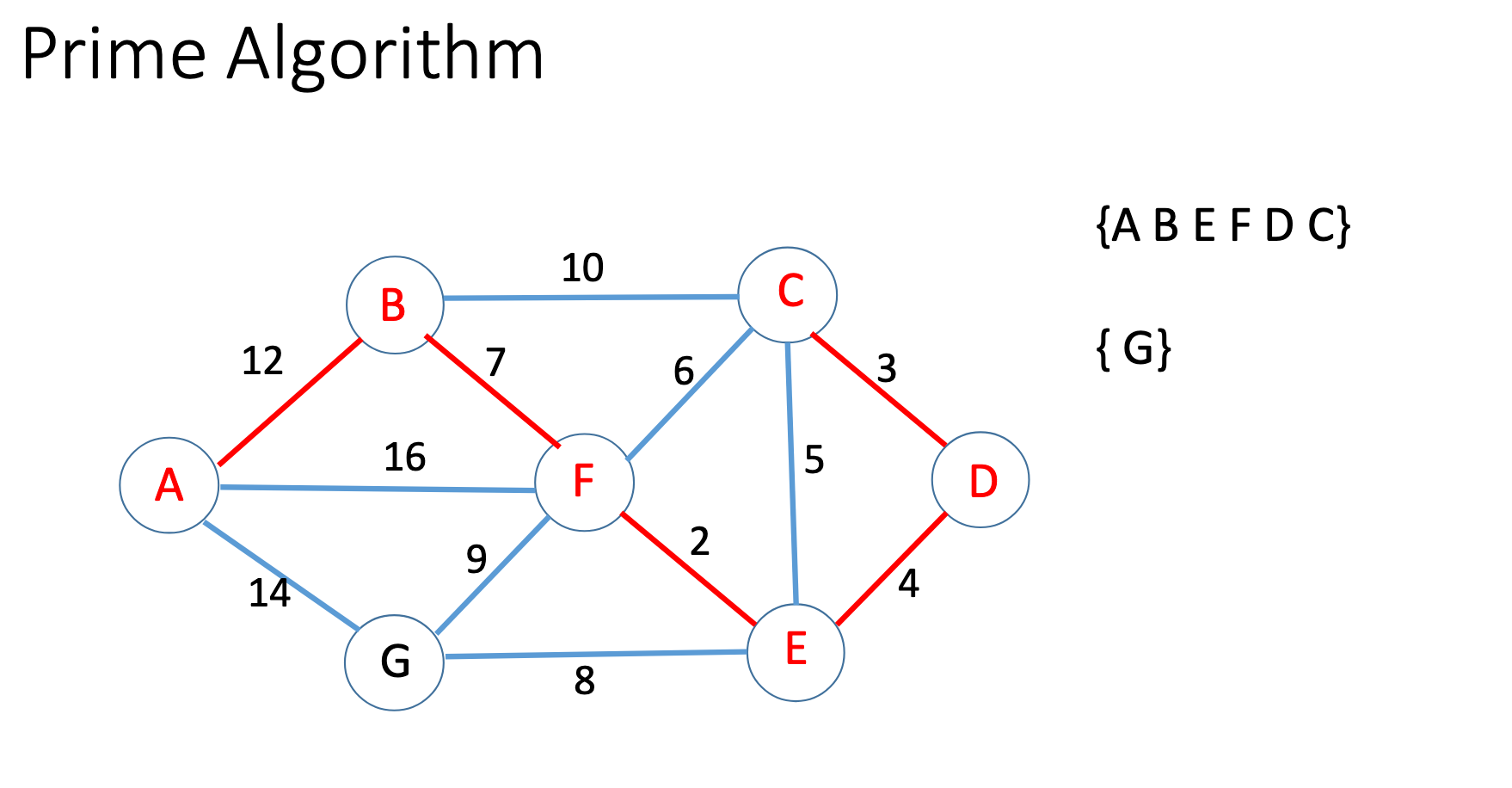
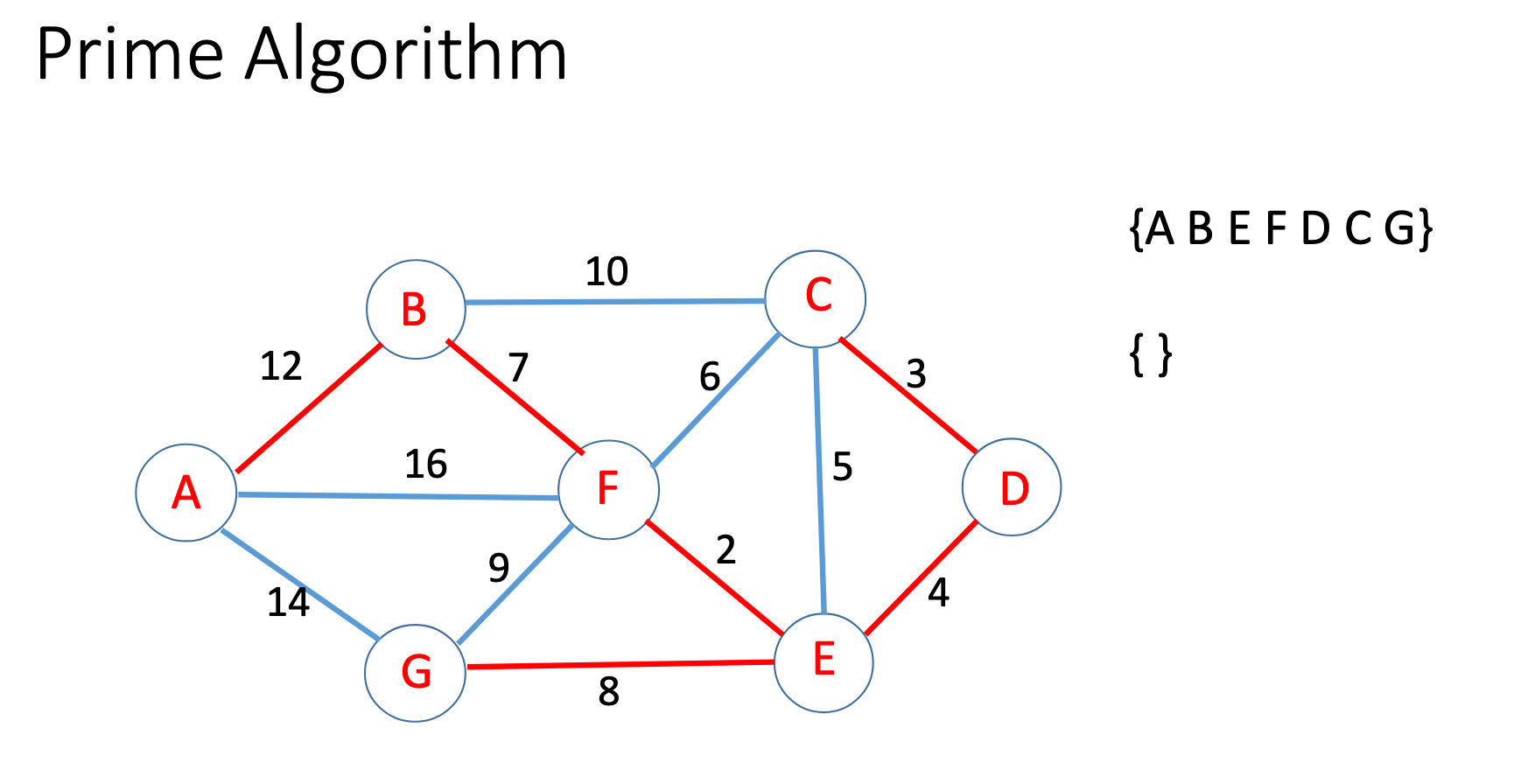
Kruskal

Huffman coding
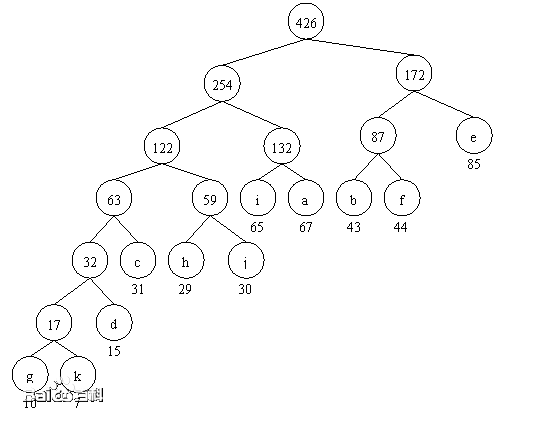
WTL algorithm (I):
Add all root nodes
WTL=17+32+63+59+122+132+87+254+172+426=1364
WTL algorithm (II):
Add all leaf nodes * layers
85 * 2 + 43 * 3 + 44 * 3...
chart
Depth first DFS
(go deep first, then back when you come to the end) stack
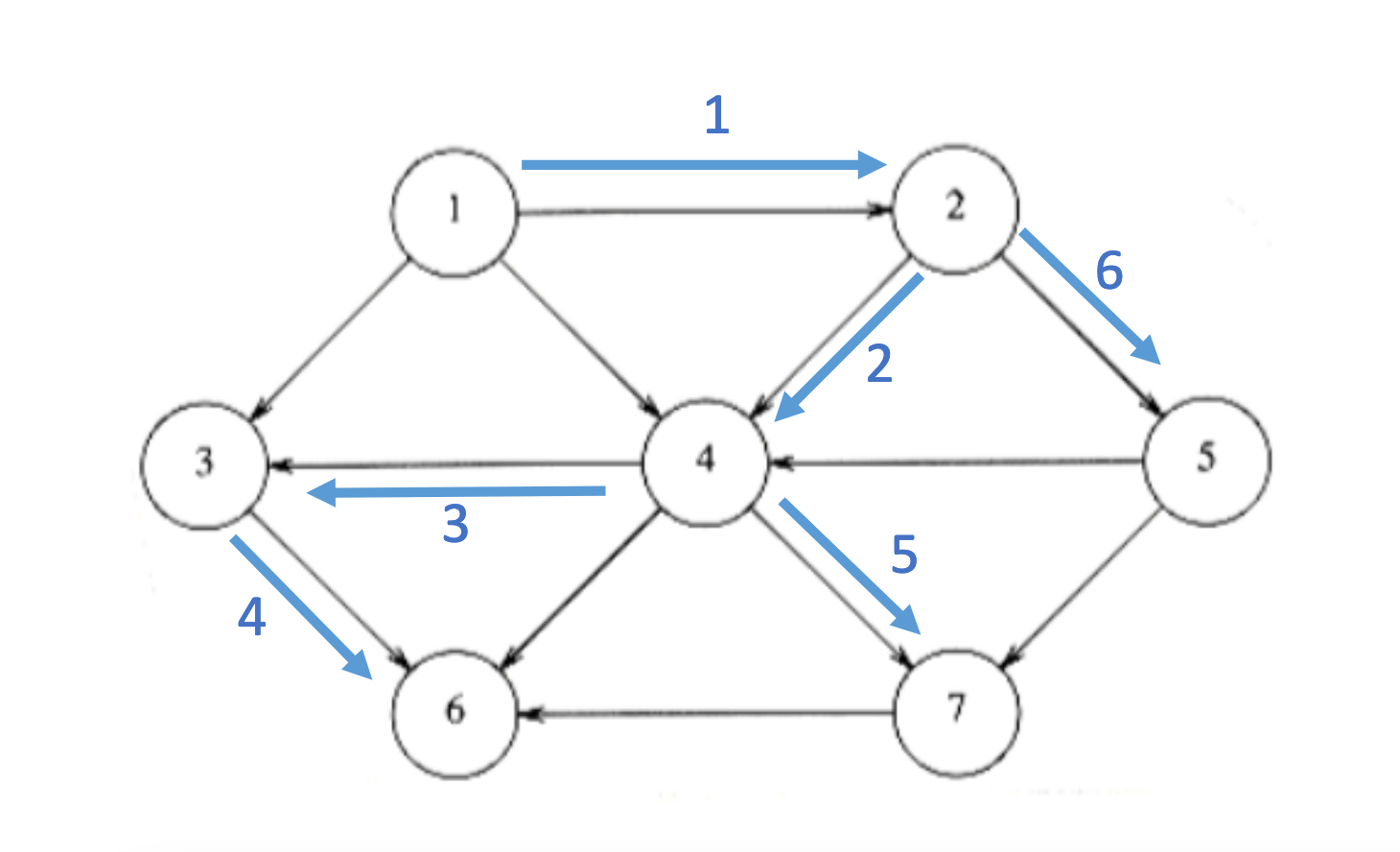
Breadth first BFS
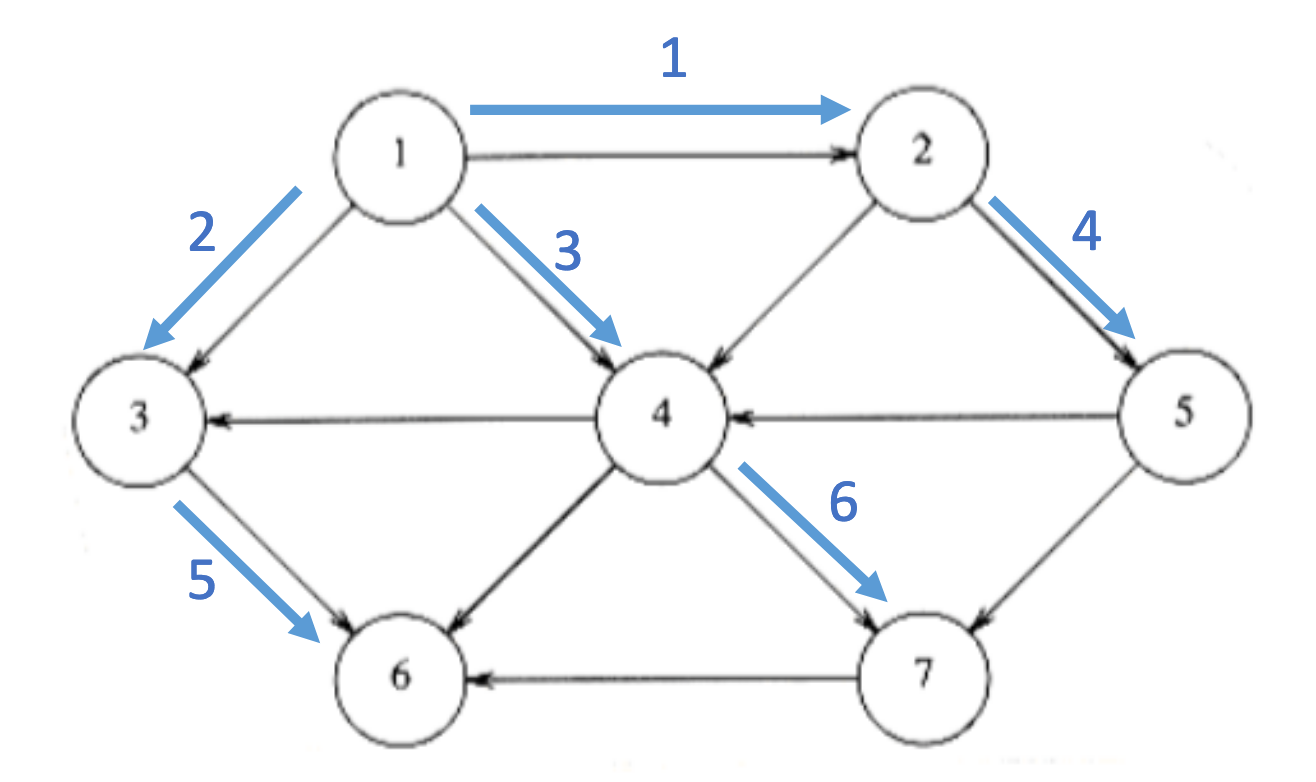
dynamic programming
Cargo carrier
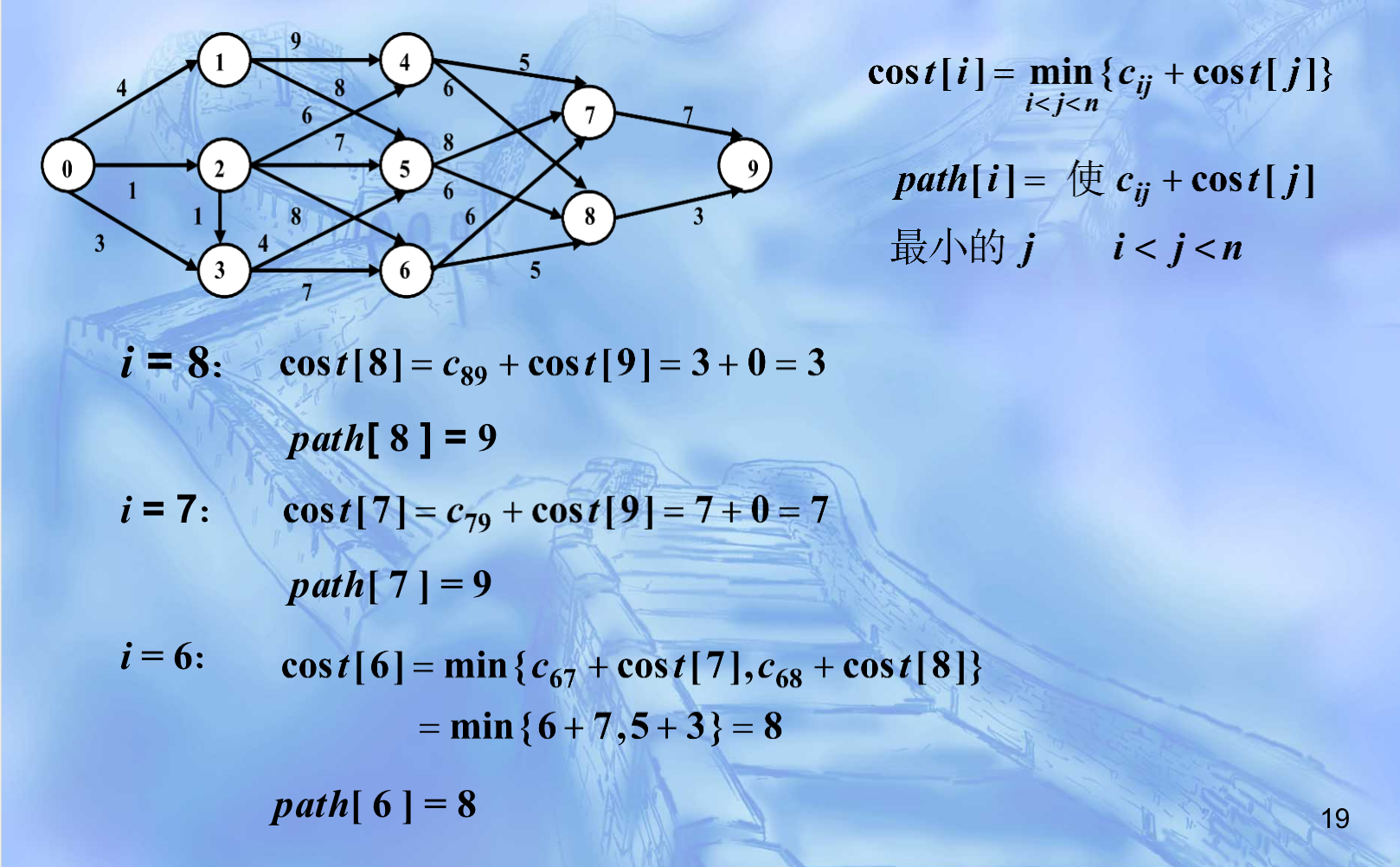
The shortest path from city 1 to city 2, 3 and 4 and back to 1 is:
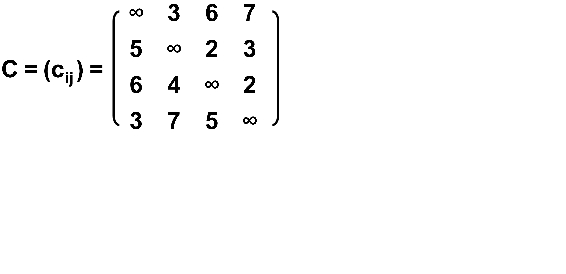

Shortest path of multi segment graph
Solve the shortest path problem shown in the figure



Longest common subsequence
String a = xyxyx B = yxxxy find the longest common subsequence
| empty set | x | y | x | x | y | x | |
|---|---|---|---|---|---|---|---|
| empty set | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| y | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| x | 0 | 1 | 1 | 2 | 2 | 2 | 2 |
| x | 0 | 1 | 1 | 2 | 3 | 3 | 3 |
| x | 0 | 1 | 1 | 2 | 3 | 3 | 4 |
| y | 0 | 1 | 2 | 2 | 3 | 4 | 4 |
1.yxxy
2.xxxy
knapsack problem
(indivisible) 6 objects, weight: 4, 2, 2, 1, 3, 2. Value: 3, 6, 5, 4, 3, 4. The load is 8
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 2 | 0 | 0 | 4 | 4 | 4 | 7 | 7 | 7 | 7 |
| 3 | 0 | 4 | 4 | 8 | 8 | 8 | 11 | 11 | 11 |
| 4 | 0 | 4 | 5 | 9 | 9 | 13 | 13 | 13 | 16 |
| 5 | 0 | 4 | 6 | 10 | 11 | 15 | 15 | 19 | 19 |
| 6 | 0 | 4 | 6 | 10 | 11 | 15 | 15 | 19 | 19 |
{0,1,1,1,0,1}
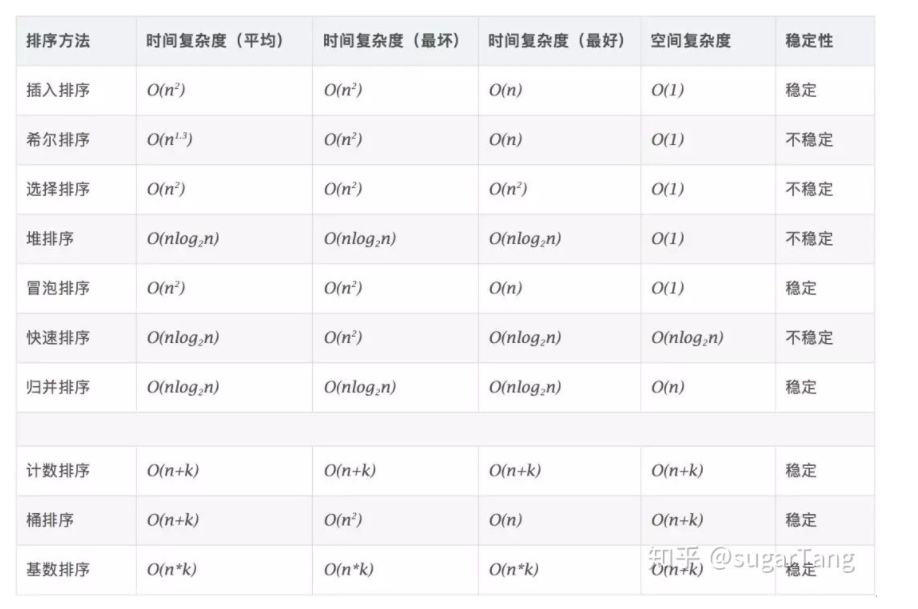
Time complexity