[algorithm] sword finger Offer special assault version Day4 array part

Title address: https://leetcode-cn.com/study-plan/lcof/?progress=wgzvtig

Objective: summarize key points and share ideas
Note: under reasonable conditions, only use the code that is the simplest to understand and practical to use

I [medium] 010 Subarray with and k

Difficulty: ordinary. It's good to understand. At first, the author was a little confused about the prefix and given in the solution

main points:

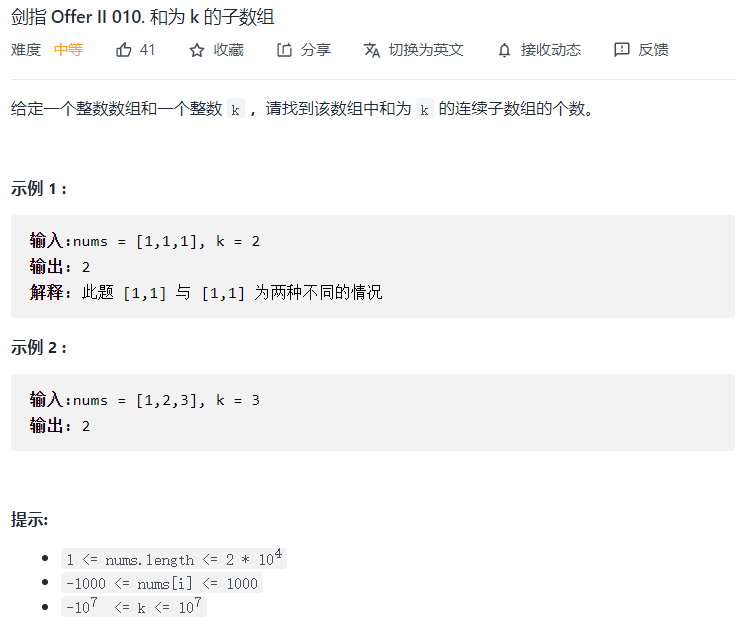
• Idea: first understand the problem according to the violent solution method. This problem can construct prefix and array presum [], so that the double cycle of presum[j]-presum[i]==k can be solved, with time complexity O ( n 2 ) O(n^2) O(n2)
• Optimization idea 1: continuous subarray can be solved by sliding window. It can't be solved after trying because there are negative numbers. Whether to slide the pointer in the left or right window cannot be determined
• Optimization idea 2: prefix and array are stored in hash table and searched while constructing
  

Quoted in Brush through the sword finger offer-Day07-array III-010 Explanation of the idea of prefix sum of k subarray)

• Personal explanation (popular explanation, please skip if you understand the above): This article is the most concise and clear among many questions, but i still don't understand how the hash table here is stored in the prefix and the difference between arrays i and j. The detailed explanation is as follows
  

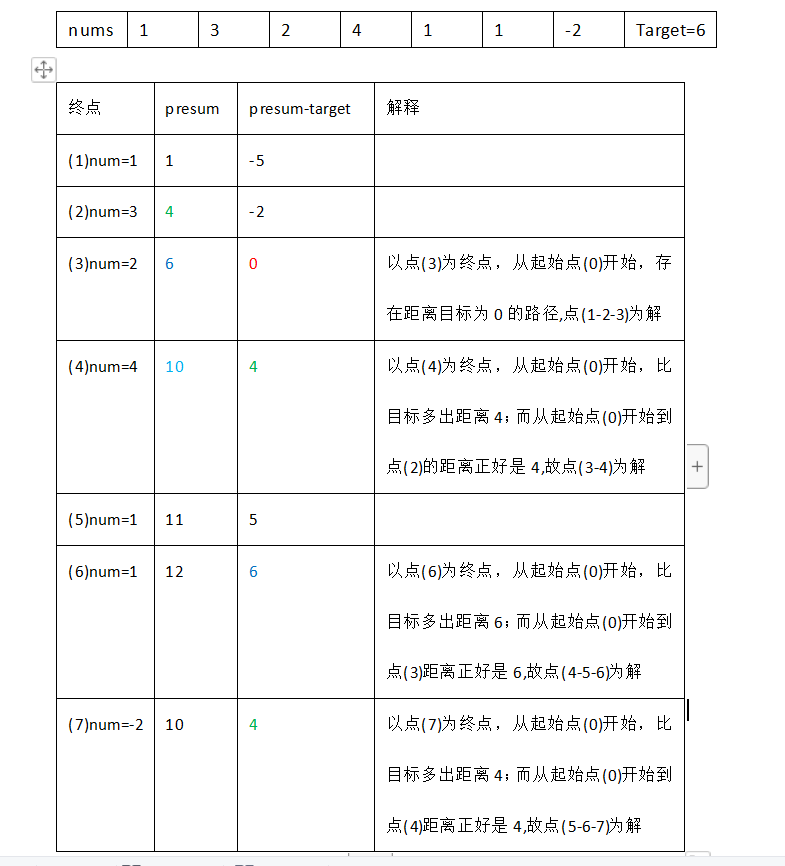
class Solution:
    def subarraySum(self, nums: List[int], target: int) -> int:
        presum = 0 # Prefix and
        dic = {0:1}   # dic[key]:value, which represents the number of occurrences of prefix and key
        ans = 0    
        for num in nums:
            presum += num
            # presum - target indicates the prefix from the starting point to the current num and the distance more than target
            # If you find a prefix just equal to this distance in the previous point, you will find the path solution
            ans += dic.get(presum-target,0) 
            # 
            dic[presum] = dic.get(presum,0) + 1 
        return ans 

II [medium] 011 0 and 1 have the same number of subarrays

Difficulty: Based on the previous question, the question is simple after changing ideas

main points:

• Idea: there are only 0 and 1 in the array, and the sliding window cannot be used without making any changes, because the effect of moving the right pointer by more 0 and the left pointer by less 0 is the same, and the moving direction of the pointer, that is, the sliding window, cannot be determined. Then why not use prefixes and algorithms directly? (the author was confused when asking and answering by himself at that time) similarly, if the prefix sum is directly used, how to determine how much the prefix sum is equal to when the condition is true
• Key: change 0 to - 1 to use the prefix sum. In this way, as long as the prefix sum is 0, the condition is met, and the topic is converted to the longest subarray with prefix sum of 0.
• Can the sliding window be used after the change? No, even if all the numbers are changed to positive numbers to meet the sliding requirements of the sliding window, how much is the sum of the numbers in the sliding window to meet the conditions?

class Solution:
    def findMaxLength(self, nums: List[int]) -> int:
        ans = 0
        dic = {0:-1} # When the prefix sum is equal to 0, it indicates that the requirements have been met, and i+1 can be used directly
        presum = 0
        for i,num in enumerate(nums):
            if not num:num=-1 # 0 Rev - 1
            presum += num     
            # Here, the hash table is assigned with else to ensure that only the earliest point is updated, so that the maximum length is obtained
            # At the same time, if the variant of this problem is to find the minimum length of the subarray, you can adjust the unconditional dictionary assignment here
            if presum in dic: 
                ans = max(ans,i-dic.get(presum))
            else:
                dic[presum] = i
        return ans

II [simple] 012 The sum of the left and right subarrays is equal

Difficulty: simple, prefix and question

main points:

• Idea: Quoted from official explanation
  

class Solution:
    def pivotIndex(self, nums: List[int]) -> int:
        sums   = sum(nums)
        presum = 0
        for i,num in enumerate(nums):
            leftSum  = presum
            rightSum = sums-leftSum-num
            if leftSum == rightSum:
                return i
            presum += num
        return -1

II [medium] 013 Sum of two-dimensional submatrix

Difficulty:

main points:

• Idea: quoted from
  Graphic prefixes and, concise ideas and complete notes
  
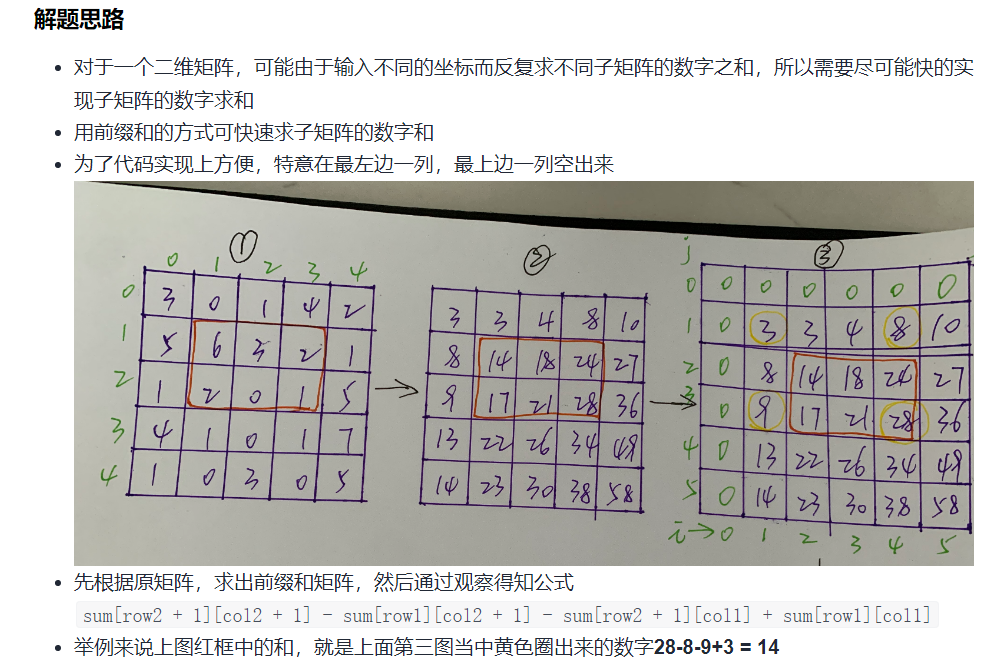
• Therefore, this question becomes how to find the prefix and matrix of two-dimensional matrix (personal understanding is a bit like a template question)

# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        rows,cols = len(matrix),len(matrix[0]) if matrix else 0
        sums = [[0] * (cols+1) for _ in range(rows+1)]
        for i in range(rows):     # y-axis down
            for j in range(cols): # x-axis right 
            	# Find the prefix sum of two-dimensional matrix
                sums[i+1][j+1] = sums[i][j+1] + sums[i+1][j] - sums[i][j] + matrix[i][j]
        self.sums = sums

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        _sums = self.sums

        return _sums[row2 + 1][col2 + 1] - _sums[row1][col2 + 1] - _sums[row2 + 1][col1] + _sums[row1][col1]