tree

Definition and related concepts of tree

Start with the linked list and diagram

Linked list

In the previous content, we learned the basic data structure of linked list. Single linked list is one of them. The structure form is as follows:

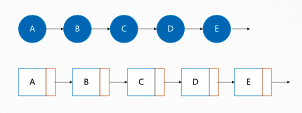
# Definition for the singly-linked list.
Class ListNod:
  def __init__(self, val=0, next=None):
    self.val = val
    self.next = next

In fact, the tree structure is similar to a single linked list, but its pointer field has multiple pointer fields

• Single linked list: one data field + one pointer field
• Tree: one data field + multiple pointer fields

chart

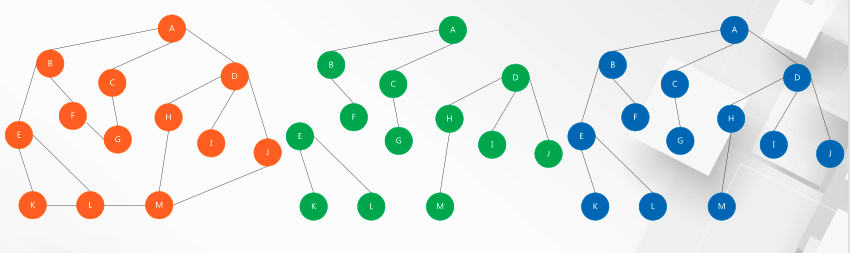
• Figure: vertex set + edge (Orange)
• Tree: acyclic connected graph (blue graph)

The difference is that each node of the graph is connected, with in and out degrees. The nodes of the tree do not require

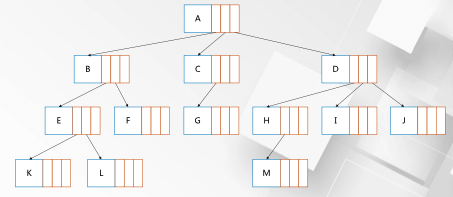
Definition of tree

The tree is N( N > = 0 N>=0 N> = a finite set of 0) nodes. N = 0 N=0 Empty tree when N=0, N > 0 N>0 N> 0 should meet:

• There is and only one specific node called root
• N > 1 N>1 N> At 1, other nodes can be divided into m( m > 0 m>0 m> 0) disjoint finite sets. Among them, each finite set itself
  It's a tree

Related concepts of tree

• Root node: the only node in the top layer of the non empty tree, and the other nodes are its descendants

• Degree of node: the number of child nodes the node has

• Leaf node: node with degree 0

• Parent child node: a pair of directly connected nodes. The parent node is in the upper layer and the child node is in the lower layer

• Sibling node: different nodes generated from the same parent node are called sibling nodes

• Node hierarchy: from the root, it is recorded as layer 1, its child nodes are layer 2, and its grandchildren are layer 3

• Node depth: the number of times the node is in the layer

• Depth / height of the tree: the maximum number of layers of the tree

• Node height: the depth / height of the subtree with the node as the root

• Ordered tree: the new tree obtained by exchanging positions of subtrees with sibling nodes as roots is regarded as a tree different from the original tree

• Unordered tree: the new tree obtained by exchanging positions of subtrees with sibling nodes as roots is regarded as the same tree as the original tree

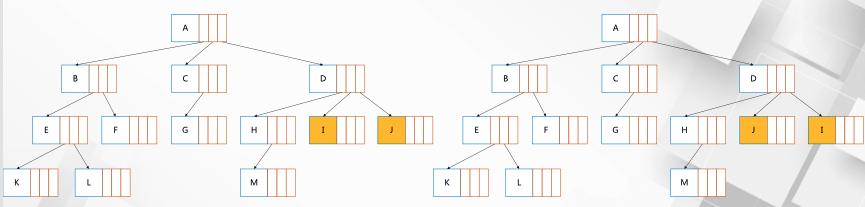
If it is a disordered tree, the above two trees can be regarded as the same tree; If it is an ordered tree, the above two trees cannot be regarded as the same tree.

Binary tree

definition

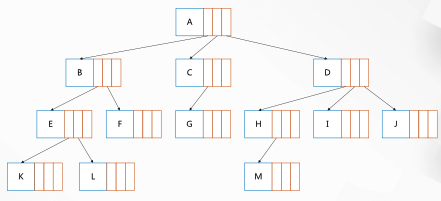
Binary tree is a kind of tree whose degree of each node is no more than 2. Among them, the child nodes of each node are divided into left and right, and the subtree where the left and right child nodes are located cannot exchange positions, that is, the binary tree is an ordered tree.

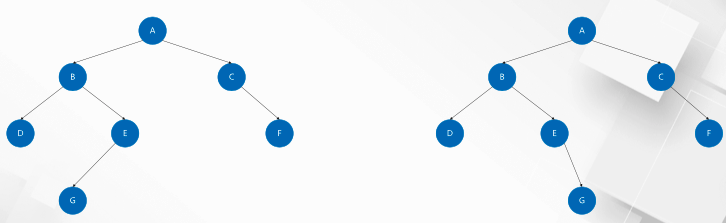
The above are two different binary trees.

Special binary tree

• Full binary tree
  • A tree in which all leaf nodes are at the bottom and all non leaf nodes have a degree of 2

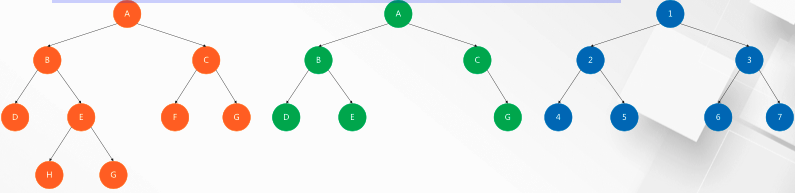
The blue tree in the above is full of binary trees.

If the height of full binary tree T is h and the total number of nodes is n, then n = 2 h − 1 n=2^h -1 n=2h − 1, the total number of nodes in layer k is 2 k − 1 2^{k-1} 2k−1

Starting from 1, number T from top to bottom and from left to right. If the node numbered i to has a parent node, its parent node number is [ i / 2 ] [i/2] [i/2], if there is a left node, its left child node number is 2i; if there is a right child node, its right child node number is 2 i + 1 2i+1 2i+1

• Complete binary tree

  • Note that the height of the binary tree is h. Starting from 1, number the binary tree from top to bottom and from left to right. Do the same numbering for full binary trees with the same height H. If the number of all nodes in the binary tree can be consistent with the number of nodes in the same position in the full binary tree, the binary tree is a complete binary tree
    

  The orange and blue trees in the figure above are completely binary trees.

The leaf nodes of a complete binary tree can only exist in the bottom two layers, and all the leaf nodes at the bottom layer are closely arranged on the left

The numbering rules between parent and child nodes in a complete binary tree are exactly the same as those in a full binary tree, and the nodes with numbers greater than [n/2]
Must be a leaf node

If n is an odd number, each non leaf node has two child nodes; If n is an even number, the n/2 node must be non leaf
Node, and it has only left child nodes but no right child nodes, and the other non leaf nodes have two child nodes

• Binary search tree (BST)
  • The binary search tree is either empty or meets the following conditions at the same time:
    • The keywords of all nodes in the left subtree are less than those of the root node
    • The keywords of all nodes in the right subtree are greater than those of the root node
    • The left and right subtrees are also binary search trees

The classic application scenario of binary search tree is to store orderly data and improve search efficiency. With the same ordered sequence, many different binary search trees can be constructed

The left and right are binary search trees, but the right is a special style, which has become a single linked list. Try to avoid this structure.

• Balanced binary tree (AVL)
  • If the height difference between the left and right subtrees of each node in the binary tree is not greater than 1, the binary tree is a balanced binary tree

The classic application scenario of balanced binary tree is to combine with binary search tree to form balanced binary search tree. While constructing the binary search tree, the height difference between the left and right subtrees of each node is not greater than 1 with the help of adjustment strategy, so as to ensure that the left and right subtrees of each node in the binary search prime tree are of the same scale, and the whole tree looks more "symmetrical".

Basic operation of tree

Storage structure of tree

• Sequential storage structure

The storage structure is basically similar to that of the graph

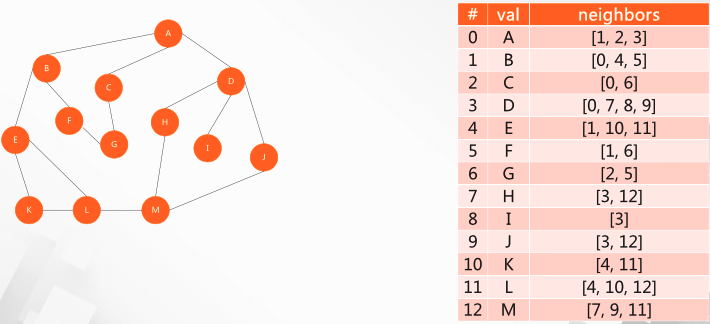
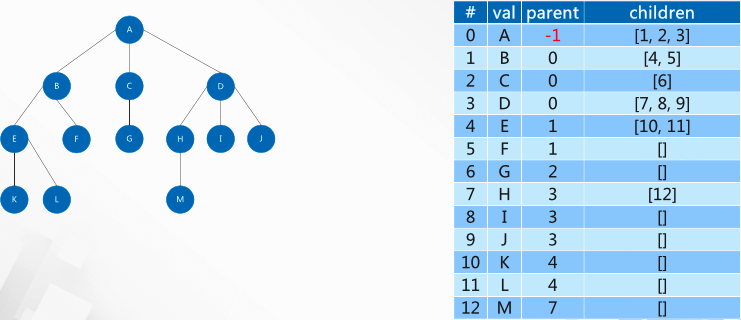
The difference is that there is a parent node column, and the parent node of the root node is set to - 1.

• Linked Storage Structure

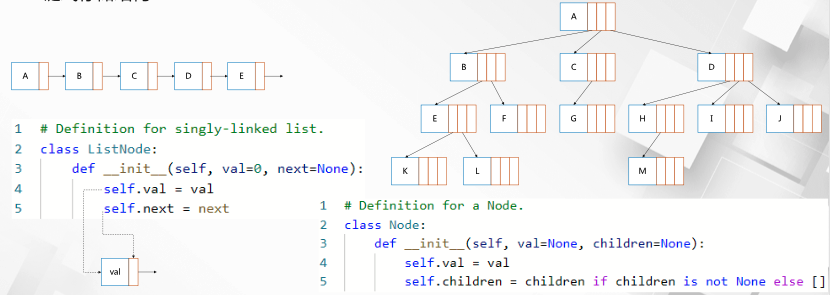
Similar to the single linked list, there are children nodes

Addition, deletion, modification and query of tree

• Addition and deletion

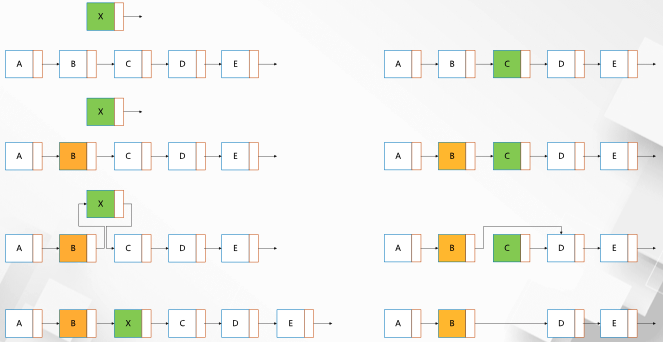
The above figure shows the insertion and deletion, which is basically similar to the single linked list.

• Find / search / traverse is the core operation of the tree

  • Traversal: access each node in the tree according to certain rules to ensure that each node will be "accessed" and each node will only be "accessed" once
  • "Access": the program interacts with the node or performs some operations on the node
  • "Enter": the program comes to a node without any interaction with the node
  • Under different rules, there may be one or more "entry" times for the same node, but the "access" to the same node will only occur once

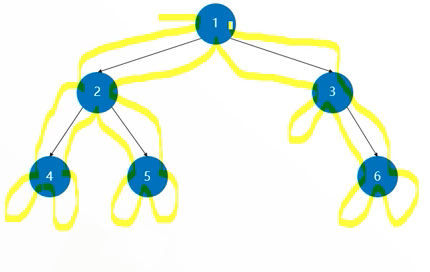
• Depth first search of binary tree (DFS)
  The depth first search of binary tree has the following conventional requirements when "entering" the node:

  • You must start the search with the root node and "enter"
  • First "enter" the left child node of the current node, and then "enter" the right child node of the current node
  • If the current node is empty or the left and right child nodes have been "entered", enter the parent node again

def dfs(TreeNode root):
  if not root:
    return
  
  print(root.val)  # Enter the current node for the first time and access it for the first time
  
  dfs(root.left)   # First enter the left child node
  print(root.val)  # Enter the current node for the second time
  
  dfs(root.right)	 # Next, enter the right child node
  print(root.val)  # Third visit
  return           # After all the left and right child nodes have entered, return to the parent node

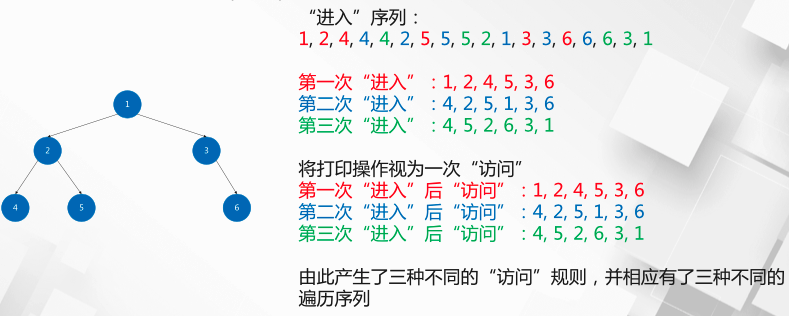
When the root node "enters" for the first time, other nodes are not "entered";

When "entering" the second time, all the nodes in the left subtree complete "entering" three times. First "access" the root, then "access" the left subtree, and finally "access" the right subtree, that is, entering "; During the third "entry", the right subtree traverses the nodes in order and completes the "entry" for three times

# Treat the print operation as an "access"
# "Access" after the first "entry": 1, 2, 4, 5, 3, 6

def dfs(TreeNode root):
  if not root:
    return
  print(root.val)
  dfs(root.left)   # First enter the left child node
  dfs(root.right)	 # Next, enter the right child node
  return           # After all the left and right child nodes have entered, return to the parent node

This is the preorder traversal: Root -- > left -- > right

When the root node "enters" for the first time, other nodes are not "entered"; In the second "entry", all the nodes in the left subtree complete three "entries". First "access" the left subtree, then "access" the root, and finally "access" the right subtree to enter "; During the third "entry", all the nodes in the right subtree complete the "entry" for three times

# Treat the print operation as an "access"
# Access after the second "entry": 4, 2, 5, 1, 3, 6

def dfs(TreeNode root):
  if not root:
    return
  
  dfs(root.left)   # First enter the left child node
  print(root.val)
  dfs(root.right)	 # Next, enter the right child node
  return           # After all the left and right child nodes have entered, return to the parent node

This is the middle order traversal: left -- > root -- > right

When the root node "enters" for the first time, other nodes are not "entered"; In the second "entry", all the nodes in the left subtree complete three "entries". First "access" the left subtree, then "access" the right subtree, and finally "access" the root and enter "; During the third "entry", all the nodes in the right subtree complete the "entry" for three times

# Treat the print operation as an "access"
# "Visit" after the third "entry": 4, 5, 2, 6, 3, 1

def dfs(TreeNode root):
  if not root:
    return
  
  dfs(root.left)   # First enter the left child node
  dfs(root.right)	 # Next, enter the right child node
  print(root.val)  # Third visit
  return           # After all the left and right child nodes have entered, return to the parent node

This is post order traversal: left -- > right -- > root

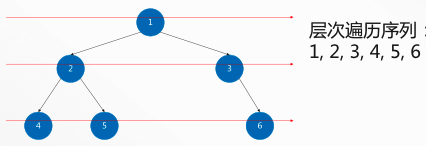
• Breadth first search (BFS) of binary tree
  Starting from the root node, each node is "accessed" from left to right in the same hierarchy from top to bottom, which is also called hierarchy traversal

  Each node "enters" only once

In order to realize the limited breadth search of binary tree, a special data structure queue is needed

The process of traversing binary tree hierarchy:

• Initialize the empty queue and join the root node into the queue
• When the queue is not empty and the queue header element is not empty, repeat the following operations continuously:
  • The queue head node is out of the queue and set as the current node
  • "Access" the current node
  • If the left child node of the current node exists, the left child node will be queued
  • If the right child node of the current node exists, the right child node will be queued

def bfs(self, root: Optional[TreeNode]):
  q = []  # queue
  q.append(root)  # Queue initialization
  while len(q) and q[0]:
    cur = q.pop()
    print(cur.val)  # visit
    if cur.left:
      q.append(cur.left)
    if cur.right:
      q.append(cur.right)
  return None

However, it is suggested to use the following writing method to add a variable of the number of nodes per layer to isolate the layer from the layer:

def bfs(self, root: Optional[TreeNode]):
  q = []  # queue
  q.append(root)  # Queue initialization
  while len(q) and q[0]:
    size = len(q)  # Record the total number of nodes in the current tier
    for i in range(size):  # The for loop is responsible for controlling node level operations in the same layer
    	cur = q.pop()
    	print(cur.val)  # visit
    	if cur.left:
      	q.append(cur.left)
    	if cur.right:
      	q.append(cur.right)
  return None

Learning video

• https://tianchi.aliyun.com/course/932/14632

The problem of tree is generally to find the depth of the tree, tree traversal, symmetric tree and so on. The general solution is dfs and bfs recursion.

Examples

88. Maximum depth of binary tree

Given a binary tree, find its maximum depth.

The depth of the binary tree is the number of nodes on the longest path from the root node to the farthest leaf node.

Note: leaf nodes refer to nodes without child nodes.

Example:

Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

Returns its maximum depth 3.

Problem solving ideas

• dfs traversal: traversal from top to bottom, to the last layer node, the depth is 0, and then slowly go up to the root node, and the height increases gradually
• bfs traversal: sequence traversal to check the number of layers, that is, the depth

dfs is usually in the form of recursion

bfs is usually completed by iterative loops

• python implementation

dfs

Set the variable tmp to record the current node depth

tmp is passed to the child node as a parameter of dfs function

Update tmp after the program "enters" the node for the first time

When "entering" an empty node, it means that the traversal of a path is completed and the result ans is updated

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        self.ans = 0
        tmp = 0
        self.dfs(root, tmp, self.ans)
        return self.ans
    
    
    def dfs(self, root: TreeNode, tmp: int, ans: int):
        if not root:
            self.ans = max(tmp, ans)
            return None
        
        tmp = tmp + 1
        self.dfs(root.left, tmp, self.ans)
        self.dfs(root.right, tmp, self.ans)
        return None

It can also be simplified to

When the program encounters an empty node, it returns the height 0 of the empty node to the parent node

When the program "enters" the node for the third time, the maximum height of its two child nodes has been calculated and returned to the node

The maximum height of the current node can be calculated according to the maximum height of the child node

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        left_high = self.maxDepth(root.left)
        right_high = self.maxDepth(root.right)
        return max(left_high, right_high) + 1

bfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # bfs
        ans = 0
        q = []
        q.append(root)
        while len(q) and q[0]:
            ans += 1
            size = len(q)
            for i in range(size):
                cur = q.pop(0)
                if cur.left:
                    q.append(cur.left)
                if cur.right:
                    q.append(cur.right)
        return ans

• C + + implementation

dfs

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr)
        {
            return 0;
        }
        else{
            int left_high = maxDepth(root->left);
            int right_high = maxDepth(root->right);
            return max(left_high, right_high) + 1;
        }
    }
};

bfs

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr)
        {
            return 0;
        }
        queue <TreeNode*> lst;
        lst.push(root);
        int ans = 0;
        while(!lst.empty())
        {
            int sz = lst.size();
            ans++;
            while(sz>0)
            {
                TreeNode* node = lst.front();
                lst.pop();
                if(node->left)
                {
                    lst.push(node->left);
                }
                if(node->right)
                {
                    lst.push(node->right);
                }
                sz--;
            }
        }
        return ans;
    }
};

92 convert ordered tree group into binary search tree

Give you an integer array nums, in which the elements have been arranged in ascending order. Please convert it into a highly balanced binary search tree.

A height balanced binary tree is a binary tree that satisfies the requirement that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1.

Example 1:

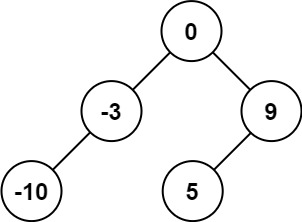
Input: nums = [-10,-3,0,5,9]
Output:[0,-3,9,-10,null,5]
Explanation:[0,-10,5,null,-3,null,9] Will also be considered the correct answer:

Example 2:

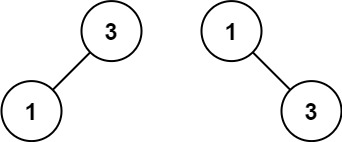
Input: nums = [1,3]
Output:[3,1]
Explanation:[1,3] and [3,1] Are highly balanced binary search trees.

Tips:

• nums is arranged in strict ascending order

Problem solving ideas

The middle order traversal of the binary search tree is a strictly increasing sequence. In addition, try to be balanced. The middle elements of the list can be used as the root node, and the left and right sides are sequential sequences. The binary search tree can be constructed recursively.

• Take the number in the middle of the array as the root node, and divide the array into two parts with roughly equal scale

• The subarray on the left of the root node is regarded as the left subtree, and the subarray on the right is regarded as the right subtree

• Repeat step 1 for the left and right subarrays Returns an empty node until the subarray is empty

python implementation

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        low = 0
        high = len(nums) - 1
        return self.helper(nums, low, high)
    
    def helper(self, nums: List[int], low: int, high: int) -> TreeNode:
        if low > high:
            return None
        mid = int(low + (high-low) / 2)
        root = TreeNode(nums[mid])
        root.left = self.helper(nums, low, mid-1)
        root.right = self.helper(nums, mid+1, high)
        return root

c + + implementation

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size()-1);
    }
    
    TreeNode* helper(vector<int>& nums, int left, int right)
    {
        if(left > right)
        {
            return nullptr;
        }
        
        int mid = left+(right-left)/2;
        
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid-1);
        root->right = helper(nums, mid+1, right);
        return root;
    }
};

Minimum depth of 95 binary tree

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes on the shortest path from the root node to the nearest leaf node.

Note: leaf nodes refer to nodes without child nodes.

Example 1:

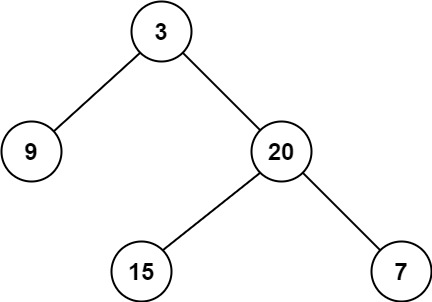
Input: root = [3,9,20,null,null,15,7]
Output: 2

Example 2:

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

Problem solving ideas:

Similar to finding the maximum depth of a binary tree, you can use dfs or bfs, just to find the minimum depth

• python implementation

dfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if not root.left and not root.right:
            return 1
        min_depth = 10**9
        if root.left:
            min_depth = min(self.minDepth(root.left), min_depth)
        if root.right:
            min_depth = min(self.minDepth(root.right), min_depth)
        return min_depth + 1

bfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if not root.left and not root.right:
            return 1

        q = []
        depth = 0
        q.append(root)
        while q and q[0]:
            depth += 1
            size = len(q)
            for _ in range(size):
                cur = q.pop(0)
                if not cur.left and not cur.right:  # As long as one node in each layer has no child nodes, it is the minimum depth
                    return depth
                if cur.left:
                    q.append(cur.left)
                if cur.right:
                    q.append(cur.right)
        return 0

• C + + implementation

dfs

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==nullptr)
        {
            return 0;
        }
        
        if(root->left==nullptr && root->right==nullptr)
        {
            return 1;
        }
        
        int min_depth = INT_MAX;
        if(root->left)
        {
            min_depth = min(minDepth(root->left), min_depth);
        }
        
        if(root->right)
        {
            min_depth = min(minDepth(root->right), min_depth);
        }
        return min_depth+1;
    }
};

bfs

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == nullptr)
        {
            return 0;
        }
        
        if(root->left == nullptr && root->right == nullptr)
        {
            return 1;
        }
        
        queue<TreeNode*> q;
        q.push(root);
        int depth = 0;
        while(!q.empty())
        {
            depth++;
            int size = q.size();
            for(int i=0; i<size; i++)
            {
                TreeNode* cur = q.front();
                q.pop();
                if(cur->left)
                {
                    q.push(cur->left);
                }
                if(cur->right)
                {
                    q.push(cur->right);
                }
                
                if(!cur->left && !cur->right)
                {
                    return depth;
                }
            }
            
        }
        
        return 0;
    }
};

96 path sum

Give you the root node of the binary tree root and an integer targetSum representing the target sum. Judge whether there is a path from the root node to the leaf node in the tree. The sum of all node values on this path is equal to the target and targetSum. If it exists, return true; Otherwise, false is returned.

A leaf node is a node that has no child nodes. This node has no left and right child nodes.

Example 1:

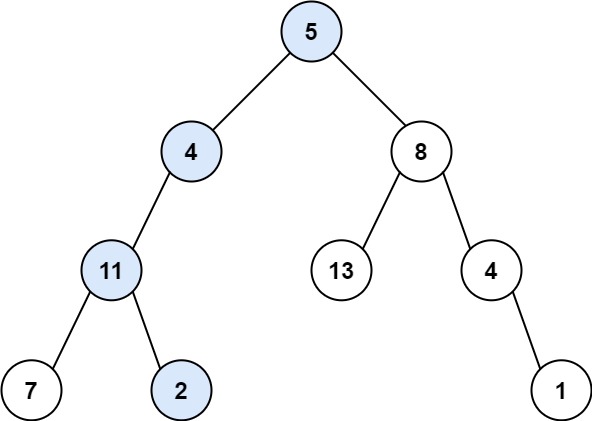
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
 Output: true
 Explanation: the path from root node to leaf node equal to the target sum is shown in the figure above.

Example 2:

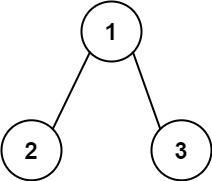
Input: root = [1,2,3], targetSum = 5
 Output: false
 Explanation: there are two paths from root node to leaf node in the tree:
(1 --> 2): The sum is 3
(1 --> 3): The sum is 4
 non-existent sum = 5 The path from the root node to the leaf node.

Example 3:

Input: root = [], targetSum = 0
 Output: false
 Explanation: since the tree is empty, there is no path from root node to leaf node.

Problem solving ideas:

By observing the function that we are required to complete, we can summarize its function: ask whether there is a path from the current node root to the leaf node, and satisfy that its path sum is sum.

Assuming that the sum of the values from the root node to the current node is Val, we can turn this big problem into a small problem: whether there is a path from the child node of the current node to the leaf, satisfying that its path sum is sum - val.

It is not difficult to find that this satisfies the nature of recursion. If the current node is a leaf node, we can directly judge whether sum is equal to val (because the path sum has been determined, which is the value of the current node, we only need to judge whether the path sum meets the conditions). If the current node is not a leaf node, we only need to recursively ask whether its child nodes can meet the conditions.

• python implementation

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        if not root:
            return False
        
        if not(root.left or root.right):  # The recursive end condition has no child nodes. You only need to judge whether the current value is consistent with the target value
            return root.val == targetSum
        
        return self.hasPathSum(root.left, targetSum-root.val) or self.hasPathSum(root.right, targetSum-root.val)

• c + + implementation

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr)
        {
            return false;
        }
        
        if(!(root->left || root->right))  // There are no child nodes. You only need to judge whether the current value is consistent with the target value
        {
            return root->val == targetSum;
        }
        
        return hasPathSum(root->left, targetSum-root->val) || hasPathSum(root->right, targetSum-root->val);
    }
};

bfs can also be used for breadth first traversal. Two queues are used for storage, one for storage node and the other for storing the path and time of the node. pop it out every time. In the title, it is required to go to the leaf node, that is, the node has no left and right child nodes. Therefore, only the path sum of this kind of node and the target path sum are judged

• python implementation

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        if not root:
            return False
        queue_node = [root]
        queue_val = [root.val]
        while queue_node:
            now = queue_node.pop(0)
            now_val = queue_val.pop(0)
            if not now.left and not now.right:  # It is required to be a leaf node without left and right child nodes
                if now_val == targetSum:
                    return True
                continue
            
            if now.left:
                queue_node.append(now.left)
                queue_val.append(now.left.val+now_val)
            
            if now.right:
                queue_node.append(now.right)
                queue_val.append(now.right.val+now_val)
        return False

• c + + implementation

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr)
        {
            return false;
        }
        
        queue <TreeNode* > q_node;
        queue <int> q_val;
        q_node.push(root);
        q_val.push(root->val);
        while(!q_node.empty())
        {
            TreeNode* now_node = q_node.front();
            q_node.pop();
            
            int now_val = q_val.front();
            q_val.pop();
            
            if(now_node->left==nullptr && now_node->right==nullptr)
            {
                if(now_val==targetSum)
                {
                    return true;
                }
                continue;
            }
            
            if(now_node->left)
            {
                q_node.push(now_node->left);
                q_val.push(now_val+now_node->left->val);
            }
            
            if(now_node->right)
            {
                q_node.push(now_node->right);
                q_val.push(now_val+now_node->right->val);
            }
        }
        return false;
    }
};

Binary search tree iterator

Implement a binary search tree iterator class BSTIterator, which represents an iterator that traverses the binary search tree (BST) in medium order:

• BSTIterator(TreeNode root) initializes an object of the BSTIterator class. The root node of BST is given as part of the constructor. The pointer should be initialized to a number that does not exist in the BST and is less than any element in the BST.
• boolean hasNext() returns true if there are numbers traversing to the right of the pointer; Otherwise, false is returned.
• int next() moves the pointer to the right and returns the number at the pointer.

Note that the pointer is initialized to a number that does not exist in the BST, so the first call to next() will return the smallest element in the BST.

You can assume that the next() call is always valid, that is, when next() is called, there is at least one next number in the middle order traversal of BST.

Example:

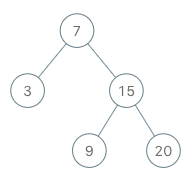
input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
output
[null, 3, 7, true, 9, true, 15, true, 20, false]

explain
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // Return 3
bSTIterator.next();    // Return to 7
bSTIterator.hasNext(); // Return True
bSTIterator.next();    // Return to 9
bSTIterator.hasNext(); // Return True
bSTIterator.next();    // Return to 15
bSTIterator.hasNext(); // Return True
bSTIterator.next();    // Return to 20
bSTIterator.hasNext(); // Return False

Problem solving ideas:

The most important property of binary search tree is that the middle order traversal of binary search tree is orderly. This topic directly "middle order traversal" to realize the ascending iterator of binary search tree.

There are two ways to solve this problem:

• Save all nodes in advance

• Calculate the next node during iteration

• python implementation

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class BSTIterator:

    def __init__(self, root: TreeNode):
        self.queue = collections.deque()
        self.inOrder(root)

    def inOrder(self, root: TreeNode):
        # Middle order traversal
        if not root:
            return None
        self.inOrder(root.left)
        self.queue.append(root.val)
        self.inOrder(root.right)
        
    def next(self) -> int:
        return self.queue.popleft()

    def hasNext(self) -> bool:
        return len(self.queue) > 0

      

# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

• c + + implementation

class BSTIterator {
private:
    void inorder(TreeNode* root, vector<int>& res) {
        if (!root) {
            return;
        }
        inorder(root->left, res);
        res.push_back(root->val);
        inorder(root->right, res);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        inorder(root, res);
        return res;
    }
    
    vector<int> arr;
    int idx;
  
public:
    BSTIterator(TreeNode* root): idx(0), arr(inorderTraversal(root)) {}
    
    int next() {
        return arr[idx++];
    }
    
    bool hasNext() {
        return (idx < arr.size());
    }
};