Nearest common ancestor of binary tree

leetcode link

1. Two solutions

Recursion - postorder traversal

Idea: this problem wants to find the nearest common ancestor of two nodes, so we have to traverse the tree from bottom to top, judge the two children first, and then judge the logic of the root node, so we think of using post order traversal.

For each node, if its left subtree has p (or q) and its right subtree has Q (or P), then the current node is their nearest common ancestor.

Therefore, we define the single-layer node operation logic:

1. If the current node is empty, return None
2. If the current node is p or q, the current node is returned

In order to transfer the results of this node to the high-level node, there should be transfer logic for each node:

1. If the value passed by the left child is not empty, it means that the left subtree of the node contains p or q, while the value passed by the right child is empty, the value passed by the left child is passed to a higher level as the return value of the node.
2. If the left child and the right child are empty at the same time, it means that the left and right subtrees of the node do not contain p and q, so pass None as the return value of the node to a higher level.
3. If neither the left child nor the right child is empty, it means that the node is the nearest common ancestor of p and q, so the value of the node is passed to a higher level as a return value

It is difficult to imagine out of thin air, so give an example to help understand:

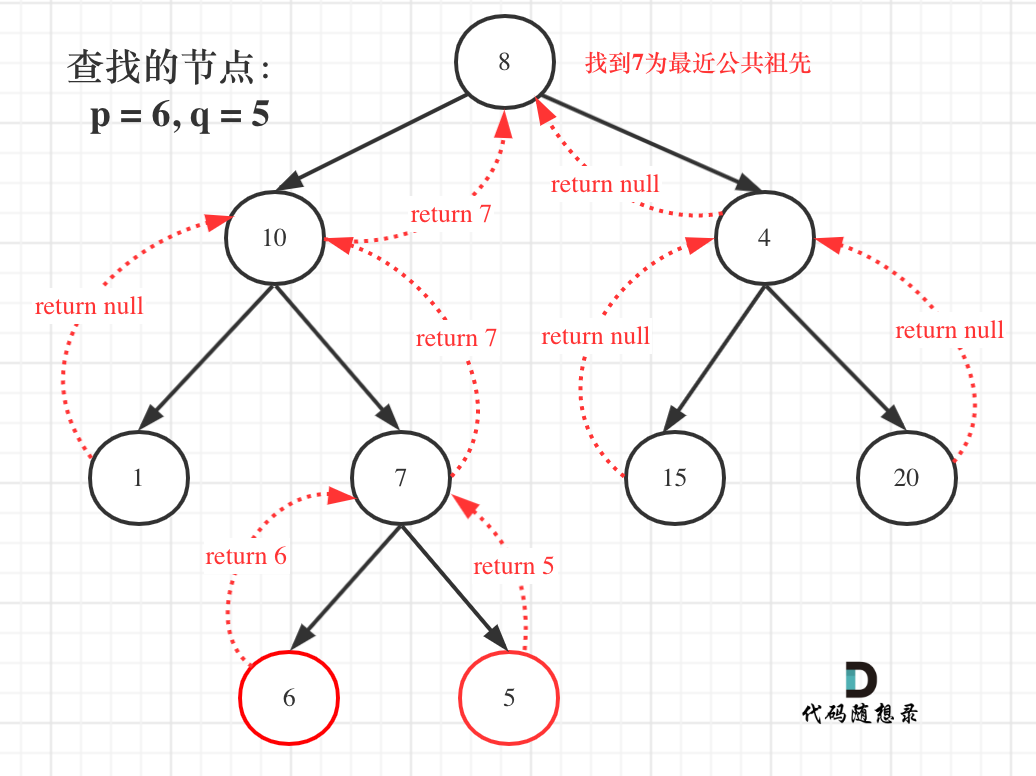
Analysis: in the figure, p is 6 and q is 5.

1. The post order traversal first traverses 1. According to the operation logic, 1 is neither p nor q nor an empty node. Then, look at the transmission logic. If both the left child and the right child are empty, both the left and right children return None. Finally, he also returns None to 10.
2. Then traverse 6. According to the operation logic, 6 is a p node, so 6 should be returned to 7, which has been returned, so there is no need to pass;
3. Then traverse 5. According to the operation logic, 5 is a q node, so 5 should be returned to 7, which has been returned, so there is no need to pass;
4. Then traverse 7. According to the operation logic, 7 is not empty, not p and q, so no operation is performed. According to the transfer logic, the left child returns 6 and the right child returns 5, which are not empty, indicating that 7 is their nearest common ancestor, so the value of the current node should be returned, that is, 7 to 10. (what we need to do now is to pass 7 to the root node, and then let the layer of the root node recursively return 7)
5. Then traverse 10. According to the operation logic, 10 is neither p nor q nor empty. According to the transfer logic, if the left child returns null and the right child returns 7, the node returns the value of the right child, that is, 7 to 8
6. Then traverse 15,... (in the same way, look at the operation logic first, and then the transfer logic)
7. Then traverse 20
8. Then traverse 4,..., and finally 4 returns None to 8
9. Then traverse 8 (root node). According to the operation logic, 8 is neither p nor q nor an empty node. According to the transmission logic, the left child (10) returns a 7 and the right child (4) returns a None, so the node must return the value of the left child, that is, 7. In this way, we pass 7 to the root node (the root node returns 7).

In combination with the code:

def lowestCommonAncestor(root, p, q):
	# Operation logic
    if root==q or root==p or root==None:
        return root

    left = lowestCommonAncestor(root.left,p,q) # Left
    right = lowestCommonAncestor(root.right,p,q) # right

	# in
	# Transitive logic
    if left and right:
        return root
    elif not left and right:
        return right
    elif left and not right:
        return left
    else:
        return None

Iterative method – sequence traversal

Idea:

Using the properties of the sequence traversal result array: for the node with index x, the index of its child node is 2x, 2x+1

Note: this property is based on the fact that all nodes in each layer should be written, that is, empty nodes should also be filled with None.

If sequence traversal is used, traverse the tree first and store the results in the result array (note that if the nodes of each layer are not satisfied, fill them with None), then we get the positions of p and q in this array, and then let them divide by 2 repeatedly until they are the positions of common nodes when they are equal.

Although I wrote the code, it will time out. I would appreciate it if someone could help me modify it to reduce the time complexity:

def lowestCommonAncestor(root, p, q):
	# Used to judge whether this layer is the last layer (the next layer of the last layer should be all None)
    def func(queue):
        for i in queue:
            if i != None:
                return True
        return False

    queue = [] 
    result = []
    indexp = -1 # Index of storage p
    indexq = -1 # Index of storage q
    count = 0 # The index used to count p and q

	'''level traversal '''
    if root:
        queue.append(root)

    while queue:
        size = len(queue) # The number of nodes in this layer is size
        # Judge whether this layer is the next layer of the last layer
        if not func(queue):
            break
		
		# Traverse this layer node
        for i in range(size):
            node = queue.pop(0)
            result.append(node)
            count += 1
			
			# Get index
            if node == p:
                indexp = count
            if node == q:
                indexq = count
			
			# Null values are filled with None
            if node == None:
                queue.append(None)
                queue.append(None)
                continue
			
			# Join the left and right children in the team
            queue.append(node.left)
            queue.append(node.right)
	''''''

	# Use indexx as the larger index and indexq as the smaller index to facilitate subsequent operations
    indexp,indexq = max(indexp,indexq),min(indexp,indexq)

	# Let's call the large index indexx divide by 2 (integer division) until < = indexq
    while indexp>indexq:
        indexp = indexp//2

	# If equal, then q is the nearest common ancestor of p and Q
    if indexp == indexq:
        return result[indexp-1]
    else: # If they are not equal, we cross divide by 2 until they are equal (because they must be equal in the end, all have the same root node)
        while indexp!=indexq:
            if indexp>indexq:
                indexp = indexp//2
            if indexq>indexp:
                indexq = indexq//2
        return result[indexp-1]

2. Summary

algorithm

We should be good at getting the key ideas from the problem stem.
For example, this problem: if we find a common ancestor through two nodes, we should first think of traversing with post order.