The best time to buy and sell stocks II

leetcode link

1. Solution

Solution 1

First of all, the first idea is to find a relatively low share price to buy, and then find a relatively high share price to sell, and then repeat. Therefore, the current problem is how to determine the position of relatively low stock price and relatively high stock price.

This question is similar to the previous one Swing sequence (for those who are not clear, please refer to my previous blog), for example:

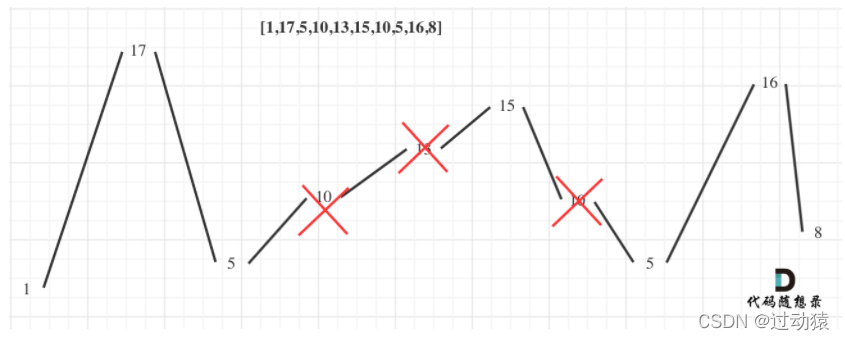
We first draw the stock price into the above shape, and then find the increasing range. The beginning and end of the increasing range is the time of buying and selling.

The increasing range in the figure above is [0,1], [2,5], [7,8]. (the interval is determined according to the index)

So we just need to (prices[1]-prices[0]) + (prices[5]-prices[2]) + (prices[8]-prices[7]) = (17-1) + (15-5) + (16-5) = 37

So we just need to find the increasing interval of the swing sequence, and then add the difference between the head and tail of all the increasing intervals, which is the final answer.

def maxProfit(prices):
    flag = 1 # flag=1 is increasing and flag=-1 is decreasing
	
	# If you start with the same numbers, only one is kept. Because the same value has no meaning for profit
    index = 0
    while index < len(prices) - 1:
        if prices[index] == prices[index + 1]:
            index += 1
        else:
            break

    prices = prices[index:]

	# After slicing, if the stock price has only one day or no more, then return 0
    if len(prices)==0 or len(prices)==1:
        return 0

	# Find the initial sequence trend
    if prices[1]>prices[0]:
        flag = 1
    elif prices[1]<prices[0]:
        flag = -1

	
    sum = 0 # Find the final answer
    start = 0 # The start position of the incremental interval is initialized to 0
    end = 0 # The end position of the incremental interval is initialized to 0
    prices.append(prices[len(prices)-1]-1) # Here, you need to add a value to prices, because the following loop cannot handle the case that the sequence is finally increasing, so you need to add a turning point. If you don't understand, you can delete this statement and submit it to see the error example.

    for i in range(len(prices)-1):
        if flag==1 and prices[i]<prices[i+1]: # If the current is increasing, and prices [i] < prices [i + 1], it proves that the monotonicity has not changed, just continue the cycle.
            continue
        elif flag==1 and prices[i]>prices[i+1]: # If the current is increasing and prices [i] > prices [i + 1], it is proved that the monotonicity changes from now to decreasing, and this is the end position of the increasing interval
            end = i # Record the end position of the incremental interval
            sum += prices[end]-prices[start] # join
            flag = -1 # Change to decrement
        elif flag==-1 and prices[i]>prices[i+1]: # If it is decreasing at this time and prices [i] > prices [i + 1], it is proved that the monotonicity has not changed, just continue the cycle
            continue
        elif flag==-1 and prices[i]<prices[i+1]: # If it is decreasing at this time and prices [i] < prices [i + 1], it is proved that monotonicity changes from this moment to increasing, and this is the starting position of the increasing interval
            start = i # Record the start position of the incremental interval
            flag = 1 # Change to increment

    return sum

Solution 2

In fact, there is an easier solution to this problem.

Let's take an example first: for example [7,1,5,10,3,6,4]. Let's look at the sub sequence of [1,5,10]. According to our above idea, we should use 10-1 = 9 to obtain the profit of this increasing range. However, this 9 can be obtained by 10-1 or (5-1) + (10-5), that is, it can be obtained by subtracting the stock price of the previous day from the stock price of the next day.

Why can we use cumulation to obtain?
The key is the default recognition in the title: you can sell or buy on the same day.

If it is stipulated that if it is sold on the same day, it cannot be purchased, then the accumulation is not established.

Therefore, we can subtract the previous value from the latter value to obtain a profit series.

For the above example, it is [- 6,4,5, - 7,3, - 2]. For this sequence, the positive number is the increasing interval and the negative number is the decreasing interval. Therefore, we can sum the positive numbers in the above sequence directly.

def maxProfit(self, prices: List[int]) -> int:
    result = 0
    for i in range(1, len(prices)):
        result += max(prices[i] - prices[i - 1], 0)
    return result

summary

When greedy, if there is no good greedy strategy for the current sequence, you can first operate the given sequence to obtain a new sequence to see if there is a good greedy strategy for the new sequence.