An introduction to the Fisher search method

Fischer search is a search algorithm that uses the Fibonacci sequence to search for specific elements from an ordered sequence.

Bipartite search divides the search interval into half each time it searches, so its search time is O(log(2)n), log(2) is the bottom log value. The Ferrett search described here uses the Ferrett series as the interval to search for the next number, so the interval converges faster and the search time is O (log n).

Algorithmic Analysis of Fehler Search

Fahrenheit search uses the Fahrenheit series to determine the search position of the next number, so it is necessary to make the Fahrenheit series first, as mentioned earlier; Fahrenheit first calculates the position of the first number to be searched and the number of Fahrenheit it it represents through a formula, so the first number of Fahrenheit is calculated for 10 numbers of the search objectThe latter must be F5, and the first location to be searched has two possibilities, such as searching in the following columns (index 0 is usually ordered to an infinite number for ease of calculation, and the columns start with index 1):

-infin; 1 3 5 7 9 13 15 17 19 20

If you want to search for 5, start the search with index F5 = 5. Next, if the number of columns is less than the specified search value, search left and right when it is greater than the number of columns. The interval between each search is F4, F3, F2. If the number of Fahrenheit is zero, the search fails, as follows:

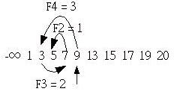
Since the value at index F5 = 5 of the first search value is less than 19, you must align the right side of the column at this point, that is, change the index of the first search value to F5+2 = 7, and search as described above, as follows:

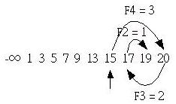
How was the first search value found?We can derive this from the following formula, where n is the number of objects to search for:

Fx + m = n

Fx <= n

That is, Fx must find a number of Fahrenheit numbers no larger than n, for 10 search objects:

Fx + m = 10

Fx = 8, m = 2, so we can compare the Fahrenheit number column to get x = 6. However, one of the possible positions of the first number is not F6, but the Fahrenheit number of x-1, which is F5 = 5.

If the number of columns at index 5 is less than the specified search value, the first search location is the location of index 5. If it is greater than the specified search value, the first search location must be added m, that is, F5 + m = 5 + 2 = 7, that is, the location of index 7. In fact, the reason for adding m is to make the next search possibleThe search just happens to be the last position in the column.

Fairchild Search seems difficult to understand, but if you know the formula Fx + m = n, it's easy to understand it by looking for a few instances yourself. In addition to fast convergence, Fairchild Search can speed up operations because it only uses additions and subtractions.

Realization of Fehl Search

#define MAX 15
#define SWAP(x,y) {int t; t = x; x = y; y = t;}

void createfib(void);               // Establishing Fahrenheit Series
int findx(int);                     // Find x value
int fibsearch(int[], int);          // Fisher Search
void quicksort(int[], int, int);    // Quick Sort

int Fib[MAX] = {-999};

//Main Program (C/OC)
int number[MAX] = {0};
int i, find;

srand(time(NULL));

for(i = 1; i <= MAX; i++) {     //Generate Random Number Column
    number[i] = rand() % 10;
}

quicksort(number, 1, MAX);      //Quick Sort

printf("Columns:");                //Print sorted columns
for(i = 1; i <= MAX; i++)
    printf("%d ", number[i]);
find = 6;                      //The object to look for
if((i = fibsearch(number, find)) >= 0)
    printf("Find number in index %d ", i);
else
    printf("\n The specified number could not be found");

printf("\n"); 

//Establish a Fernandian series to find MAX+1 Fibonacci numbers in total
void createfib(void) {
    int i;
    Fib[0] = 0;
    Fib[1] = 1;
    
    for(i = 2; i < MAX; i++)
        Fib[i] = Fib[i-1] + Fib[i-2];
}

//Find x value
int findx(int n) {
    int i = 0;
    while(Fib[i] <= n)
        i++;
    i--;
    return i;//Find the i Fib element less than or equal to MAX+1
}

//Expensive Search
int fibsearch(int number[], int find) {
    int i, x, m;
    
    createfib();                    //Create Fibonacci Sequence
    
    x  = findx(MAX+1);              //The number x in the Fibonacci series is just no greater than MAX+1.MAX is deterministic, so the starting point for comparison is deterministic.
    m = MAX - Fib[x];               //A small difference is obtained.The value of m is also determined.
    printf("\nx = %d, m = %d, Fib[x] = %d\n\n",
           x, m, Fib[x]);
    
    x--;
    i = x;
    
    if(number[i] < find)            //The initial value of i is also determined.PS: This is the power of formulas
        i += m;
    
    while(Fib[x] > 0) {             //Search, x value is decreasing, range is getting smaller and finer
        if(number[i] < find)        //Less than the value being searched
            i += Fib[--x];          //Right Shift Search Location
        else if(number[i] > find)   //Greater than the value being searched
            i -= Fib[--x];          //Move left to search for location
        else
            return i;               //Equal, find
    }
    return -1;                      //Search steps have been minimized or not found, search ended
}

//Quick Sort
void quicksort(int number[], int left, int right) {
    int i, j, k, s;
    
    if(left < right) {
        s = number[(left+right)/2];
        i = left - 1;
        j = right + 1;
        
        while(1) {
            while(number[++i] < s) ;        // Look right
            while(number[--j] > s) ;        // Look Left
            if(i >= j)
                break;
            SWAP(number[i], number[j]);
        }
        
        quicksort(number, left, i-1);       // Recurse to the left
        quicksort(number, j+1, right);      // Recurse to the right
    } 
}