dynamic programming

• Use history (results of subproblems) to avoid repeated calculations.
• History records need to be saved with some variables. There are more one-dimensional arrays and two-dimensional arrays.

My problem solving steps

1. Clarify the meaning of dp array, that is, the definition of history.
2. Find out the relationship between array elements, such as dp[n] = dp[n-1] + dp[n-2].
3. Find the initial value because the relationship needs an initial value to end. But be sure to find it all!

Examples

1. The best time to buy and sell stocks (IQ questions, dynamic programming)

From LeetCode121

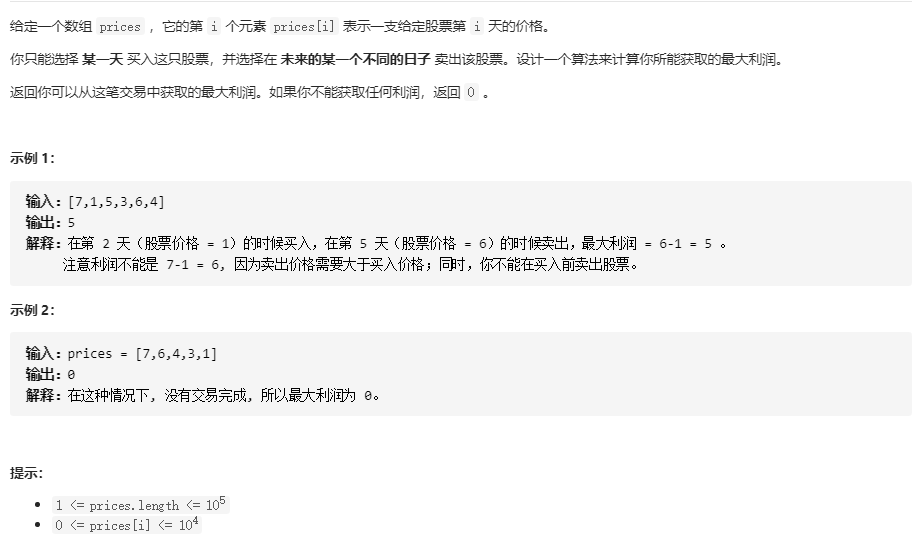
solution

1. IQ questions

• There are no other requirements (such as length, time, etc.) except that the large number should be after the decimal.
• Therefore, it can be concluded that only the front minimum value and the rear maximum value need to be obtained, and the difference between the two sides must be the maximum profit.
• And because it is limited to large numbers after decimals, there will be no omission in this method. (when there is a smaller number than the original min, if there is a number that can make max larger, the profit of the original min will be less than the new Min profit.)

class Solution {
    public int maxProfit(int[] prices) {
        int max = 0;
        int min = Integer.MAX_VALUE;
        for(int now : prices){
            if(now<min)
                min = now;
            else if(now - min > max)
                max = now - min;
        }
        return max;
    }
}

2. Dynamic programming

• My rough solution

class Solution {
    public int maxProfit(int[] prices) {
        int min;
        int[] dp = new int[prices.length];
        if(prices.length==1)
            return 0;

        dp[0]=0;
        if(prices[1]>prices[0]){
            dp[1] = prices[1] - prices[0];
            min = prices[0];
        }
        else{
            dp[1] = 0;
            min = prices[1];
        }
        

        for(int i = 2;i<prices.length;i++){
             if(prices[i]<min)
                min = prices[i];
            dp[i] = Math.max(dp[i-1],prices[i]-min);
         }
         return dp[prices.length-1];
    }
}

Very rough, spatial complexity O(m*n), too high. An optimization algorithm for dynamic programming is needed.

• Big guy solution

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length <= 1)
            return 0;
        int min = prices[0], max = 0;
        for(int i = 1; i < prices.length; i++) {
            max = Math.max(max, prices[i] - min);
            min = Math.min(min, prices[i]);
        }
        return max;
    }
}

Understanding (not guaranteed to be correct)

nothing

2. Different paths

From LeetCode62

solution

1. My dynamic planning

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];

        for(int i = 0;i<m;i++){
            dp[i][0] = 1;
        }
        for(int i = 0;i<n;i++){
            dp[0][i] = 1;
        }


        for(int i = 1;i<m;i++){
            for(int j = 1;j<n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
}

The space complexity is m*n, which needs to be further optimized.

2. After dynamic programming optimization

To be added.

understand

• Be sure to determine the definition and initial value of dp array!!!!

3. Minimum path sum (different directions of different paths)

From LeetCode 64

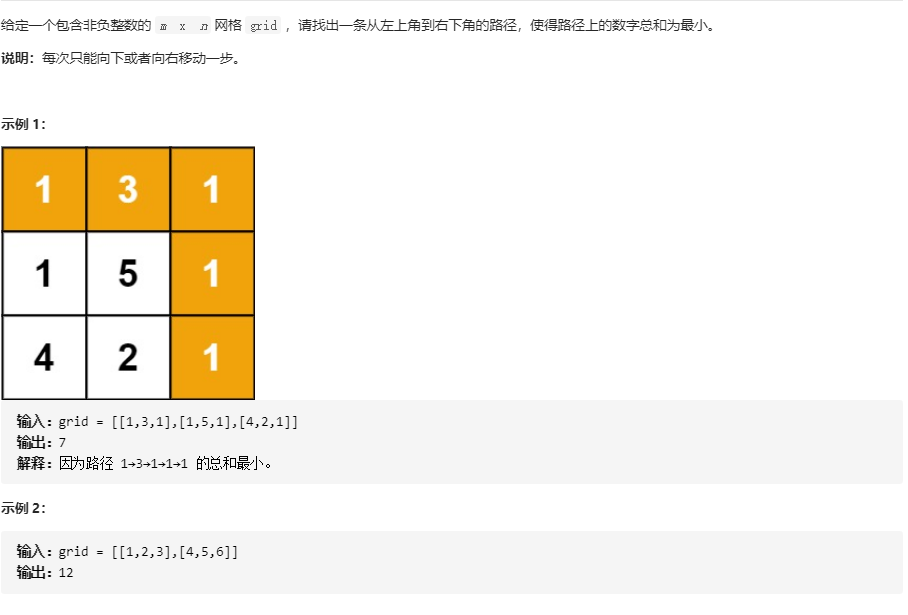
solution

1. My dynamic planning

class Solution {
    public int minPathSum(int[][] grid) {
        int[][] dp = new int[grid.length][grid[0].length];
        dp[0][0] = grid[0][0];
        for(int i = 1;i<grid[0].length;i++){
            dp[0][i]=dp[0][i-1]+grid[0][i]; 
        }

        for(int j = 1;j<grid.length;j++){
            dp[j][0] = dp[j-1][0] + grid[j][0];
        }

        for(int i = 1;i<grid.length;i++){
            for(int j = 1;j<grid[0].length;j++){
                dp[i][j] = Math.min(dp[i][j-1],dp[i-1][j]) + grid[i][j];
            }
        }

        return dp[grid.length-1][grid[0].length-1];

    }
}

The space complexity is 0(m*n), which can be optimized.

2. Dynamic programming optimization.

Learn before you do it.

understand

None.