Preface

This is a job in the process of learning algorithm analysis and design. The main purpose of this job is to clarify the problems of this job and some personal thinking. This article does not explain why to design dynamic planning algorithms like this. (Four steps to consider, etc.)

I am a student. I published an article for the first time (actually my homework). If there are any deficiencies, please forgive me. (limited ability after all)
Hope you can help

Job 1 on PPT (explain 01 backpack problem process):

Description of title: There is a bag with a capacity of 22 and five items to be loaded. The most valuable way to load is to find a typical 0-1 backpack problem. A simple algorithm is to try out all possible combinations of goods and find the one with the highest value. To improve efficiency we introduced a memo, but a better approach (a more optimized approach) is the general practice of dynamic planning: applying solutions from the bottom up.

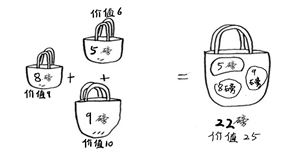
Chart: Each dynamic planning algorithm starts with a grid with rows representing selectable goods listed as backpacks of different capacities (1 to 22). Analyzing and solving dynamic programming problems is generally divided into four steps. The 01 knapsack problem is similar to the circuit routing problem, but differs from the partial knapsack problem with greedy algorithms. Due to the utilization of backpack space, the cost-effectiveness issue cannot be considered solely. The main problem in this topic is the specific solution process, which is shown in the following figure. This problem is a simpler problem in dynamic programming because for each small problem, only two cases need to be considered, one is not in the backpack. In a bottom-up representation, each value in the table needs to use either the upper or upper left values (derived from a recursive relationship), and with the relationships between tables, the order in which the tables are filled out is also present.

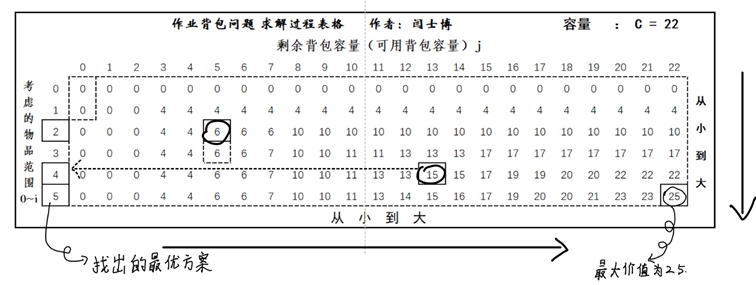
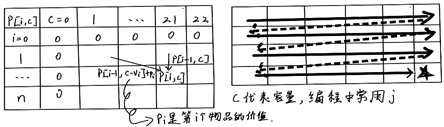
Solving process: First row, first column, is 0. Column 1: Because if the backpack is 0, the item cannot be loaded inside, the total value is 0; Line 1: The total value is 0 because if the range of items considered for loading a backpack is 0 to 0, then no items can be loaded. (Actually initialized at the time of implementation, every location of the form is 0), and then fill in the form. Because we found the relationship between the table and the view, each location fills in the form by first checking if the second item can be put in the backpack (the ticket mentioned in the class). If not, there is only one case. The maximum price is equal to the maximum value for that capacity when the range of items is 0 to i-1 (the value above the table is pulled down directly). If there is an entrance ticket (which can be put in the backpack), consider whether it is put in the backpack or not. Which situation has the greatest value, so as indicated in the table above, the value of the backpacked item is that if it is loaded, the remaining capacity of the backpack without the item is the current capacity minus the weight of the current item (weight in this topic, can also be volume) The maximum value (the best solution of the subproblem) plus the price of the current item (the upper left corner), if not loaded, is similar to the situation without an entry ticket. Comparing these two values, the greater is the maximum value of the current situation.
Solution: When items numbered 2, 4, 5 are loaded, the value in the backpack is the highest, the maximum value is 25, and the remaining space in the backpack is 0.
Code and Time Complexity: Time and space complexity is O(nc), the main code below (and print code for ancillary use, etc.)

int const NumObj = 5;				//Number of objects
int const capacity = 22;				//Back Containment
int w[NumObj + 1] = { 0 , 3 , 5 , 7 ,8 ,9 };		//Weight of each item
int v[NumObj + 1] = { 0 , 4 , 6 , 7 , 9,10 };		//Value of each commodity

int dp[NumObj+1][capacity+1] = { { 0 } };		//Optimal Value Table, Dynamic Planning Table
int item[6];					//Accessing the optimal solution (or not)

void optimalSolution() {				//Dynamic Planning, Filling in Forms, Calculating Optimal Solutions
	for (int i = 1; i <= NumObj; i++) {		//For each item, fill out the form line by line, considering one more item at a time
		for (int j = 1; j <= capacity; j++) {	//Increase capacity range, fill in form
			if (j < w[i])		//Determine if there are tickets
				dp[i][j] = dp[i - 1][j];
			else			//Consider two scenarios when you have an entry ticket and compare them to be optimal
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
		}
	}
}

void Construct(int i, int j) {				//Construct the optimal solution (the process is illustrated in the previous diagram)
	if (i >= 0) {
		if (dp[i][j] == dp[i - 1][j]) {		//Similar to circuit wiring and comparison with above values
			item[i] = 0;		//0 means this item was not selected
			Construct(i - 1, j);
		}
		else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
			item[i] = 1;		//1 represents the selected item
			Construct(i - 1, j - w[i]);				
		}
	}
}

2. Title p80 3-4 on the book (since they are all backpack problems, another PPT will be discussed later): Two-dimensional backpack problem

Think: Continue with the previous thought. Normal backpack problems only consider weight (like the above question) or volume. Now consider both. There is one more variable, which naturally requires multiple dimensions. Previously it was a flat table, but now it has become a three-dimensional table. Following the thinking of the previous question, the admission ticket should now be a condition where both the quality and volume of the ticket meet the requirements for placing in a backpack, or if the condition is not met when filling out the form, the volume and capacity of the object will be left behind. If you can put in a ticket then compare, generally use P or m to represent the optimal price, compare P (i-1, j, k) with P (i-1, j-wi, k-bi) +p i, where j represents the remaining capacity C (c in the previous question), K represents the remaining volume, and P I is the price of the current item. Of course, this is only a natural generalization, and the right and wrong and details should be carefully considered. If you fill in a form like this, the form will be a 3-dimensional one, each layer represents the extent of the object, and the horizontal and vertical coordinates of each layer are the remaining capacity and volume. If you follow the previous formula, the solution to the current problem is to need a lower level solution, possibly a value directly below (filling in the table from low to high). It may also be a value that implements the direction of the origin, so each layer can be completed as long as the previous table completes the table for that layer. Below I draw a 3-D color stereo for easy understanding, but because the print is black and white, I don't know what the result will be.


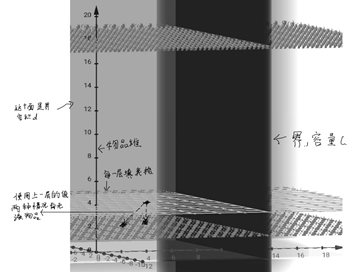
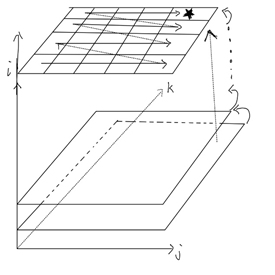
To be precise: Referring to the previous question, I created an item array to store the optimal case, where the value is either 0 or 1. When constructing the optimal solution, if 0 means that the item was not selected and if 1 means that the item was selected, the question for this question is represented by this array: \mathbf{max}{\sum_{i=1}^{n}{x_i\timesv_i}, of course, with two restrictions. The limitation is that the total capacity and volume do not exceed the range, so we get a recursive formula: if there is no ticket, p(i, j, k) = p(i-1, j, k) uses p to represent value in order to be consistent with the previous question, and if there are tickets, p(i, j, k) = max{p(i-1, j, k), p(i-1, j-wi, k-bi) +vi}, These two formulas describe the above content, so I try to change the code on the basis of the first topic to complete this problem. Dynamic planning time complexity is generally very good analysis, for O (n C d), n items, capacity is c, volume is d.

int const NumObj = 5;							//Number of objects
int const capacity = 22;							//Backpack volume (quality)
int w[NumObj + 1] = { 0 , 3 , 5 , 7 ,8 ,9 };					//Weight of each item
int v[NumObj + 1] = { 0 , 4 , 6 , 7 , 9,10 };					//Value of each commodity

//Xin Jia: (Fiddle up a number and run it to see if you can find the best one)
int const volume = 25;							//Backpack space size (volume)
int c[NumObj + 1] = { 0 , 4 , 4 , 9 ,10 ,16 };					//Volume occupied
//Change, add a dimension
int dp[NumObj + 1][capacity + 1][volume + 1] = { {0} };				//Optimal Value Table, Dynamic Planning Table

int item[6];								//Accessing the optimal solution (or not)

void optimalSolution() {							//Dynamic Planning, Filling in Forms, Calculating Optimal Solutions
	for (int i = 1; i <= NumObj; i++) {					//For each item, fill out the form line by line, considering one more item at a time
		for (int j = 1; j <= capacity; j++) {				//Increase capacity range, fill in form

			//One more cycle, the logic is the same
			for (int k = 1; k <= volume; k++) {
				if (j < w[i] || k < c[i])				//Determine whether there are tickets, note Yes or
					dp[i][j][k] = dp[i - 1][j][k];		//The logic is simple.
				else					//Consider two scenarios when you have an entry ticket and compare them to be optimal
					dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - w[i]][k - c[i]] + v[i]);
			}
		}
	}
}

void Construct(int i, int j,int k) {						//Construct the optimal solution (the process is illustrated in the previous diagram)
	if (i >= 0) {
									//One more k, the logic is exactly the same
		if (dp[i][j][k] == dp[i - 1][j][k]) {				//Similar to circuit wiring and comparison with above values
			item[i] = 0;					//0 means this item was not selected
			Construct(i - 1, j,k);
		}
		else if (j - w[i] >= 0 && dp[i][j][k] == dp[i - 1][j - w[i]][k - c[i]] + v[i]) {
			item[i] = 1;					//1 represents the selected item
			Construct(i - 1, j - w[i], k - c[i]);
		}
	}
}

The code changes independently according to the code in the previous question. Finally, it is calculated that the maximum value for this data is 22 (item 2, 3, 4). In order to make this example not select item 5 and slightly increase the volume of item 5, the data is completely self-compiled. The code is marked with comments where the changes to the above topic have been made, and the program is proven to work perfectly.

After the analysis of the first question, this question is actually very simple, as long as it is popularized along the ideas. In fact, there is also a way of thinking, that is, to build a structure, which may be closer to the way of thinking of the previous topic, can also be seen as two-dimensional, but for the implementation, but such promotion is easier and better understood.

3. Job 2 on PPT (writing algorithm), coin problem:

Above: This question is to solve the minimum coin problem, which is similar but different from the backpack problem. And when you do this, you always wonder if the greedy algorithm can also be used, and try it after you finish the job (the greedy algorithm is mainly to prove its correctness and is easy to understand). This topic can be thought through in the steps of solving dynamic planning, which is to find relationships. If you find relationships between grids and think about them, it is very simple. The best way to quickly find solutions to dynamic planning is to practice and think for yourself when you encounter problems.

In fact, the optimal substructure of the problem is very simple, that is, to increase the number of coins one at a time, can be a different coin or the same coin, so there is a double loop in my code that actually takes into account one more coin at a time. Continuously update tables (or multidimensional tables, one row at a time, the same). Update table values represent how much coins can be used to collect money for the current par value. If it is infinite, it means that coins cannot be used. The optimal substructure is to consider whether to use the current coin, which is similar to the backpack problem. Let's start with the code, each line of code with an explanation of why I wrote this, and then move on. Code:

#include <iostream>
#include <algorithm>
using namespace std;

int main() {   

    //The following data structures can be defined according to the title. The names correspond to the title.
    int m;                                  //m represents the amount of money to find
    int n;                                  //N denotes the kind of coins you have, such as three kinds of coins, one yuan, two yuan and five yuan. As you know, n is up to 2000
    int T[20001];                           //T is an array of face values. According to the title, there can be up to 20001 face values, if there is only one coin per face value
    int Coin[20001];                        //Number of coins for each face value
    int const infinite = -1;       //Defines that the initial value is infinite and -1 represents infinity
    long long int dp[20001] = {infinite};   //Define the optimal table and initialize it, all locations are infinite, or use the memset initialization function
    memset(dp, infinite, sizeof(dp));
    //Note: Here is an optimization, which should have been a two-dimensional table. In order to save space, one-dimensional tables are used to continuously evaluate in one row, and override when better is encountered.


    //Define a set of data for testing, or cin input, using five common coins
    n = 5;
    T[0] = 1; Coin[0] = 3;
    T[1] = 2; Coin[1] = 3;
    T[2] = 5; Coin[2] = 3;
    T[3] = 10; Coin[3] = 5;
    T[4] = 20; Coin[4] = 1;
    m = 48;
    //The best option is to use one 20, two 10, one 5, one 2, one 1, 6 coins, which can be correctly calculated by this program
    dp[0] = 0;                                  //Initially, use 0 coins

    //Fill in the form to evaluate, note the boundary equal sign here
    for (int i = 0; i < n; i++)                 //Coins per face value
        for (int j = 1; j <= Coin[i]; j++)      //Number of denominated coins
            for (int k = m; k >= T[i]; k--)     //The amount of money to look for, initially m, circulates when it is larger than the face value of the current coin, the amount of each money is -1;
                //When the optimum is not infinite (that is, when the value is available, the coin can be used to find m), and if the current face value coin is used, the k-when the current face value can be calculated
                if (dp[k] != infinite && dp[k - T[i]] != infinite)          
                    //Note here the understanding, comparison, subproblem optimization, in order to optimize the use of a one-dimensional array, because only the number of titles, if m and m can be calculated minus the current face value
                    //Find which case uses fewer coins, of course the second level of circulation is the number of coins, because when j = 1 is calculated once, the table is updated, note that there is an update everywhere
                    //When there are two identical coins, the second update is based on the first update, such as the face of 20, the first update, qp[10]= 1, and the second update table, dp[20], is equal to 2.
                    // Simply put, add one coin at a time
                    //Details will be discussed in more detail in the job, which is a simple understanding
                    dp[k] = min(dp[k], dp[k - T[i]] + 1);   
                else if (dp[k - T[i]] != infinite)
                    dp[k] = dp[k - T[i]] + 1;

    //The second is more human
    //cout << (dp[m] != infinite ? dp[m] : -1) << endl;
    if (dp[m] != infinite)
        cout << "The number of coins required is:" << dp[m] << endl;
    else
        cout << "Cannot use the current coin to make a figure m" << endl;
}

Code: Because the code is written entirely by myself, I have written out why I wrote it this way, and some thinking. The symbols used in it correspond to the title. DP is generally used to represent the table of optimal values, and DP is also used here following this naming convention. When you look at the code and combine it with the previous explanation, you'll see my idea. It's exactly like a backpack problem. Consider using or not using the current coin. Time complexity is easy to analyze, and time complexity is O(num) × M), num is the number of coins, size is ni multiplied by the sum of Coin i (it should be OK if you analyze it yourself). Continue with the previous discussion and update the form once each time. The first update is only one coin, of course only a DP [coin denomination] value can be compiled out, and then it can be updated again. If you can compose a denomination k and you can't do it before, that is, else if you can compose the denomination k before, you can fill in the form directly. If you can also compose this denomination k before, you can compose it now. Then compare and see which case uses fewer coins. If you can't come up with one, you still need an infinite number of coins to save it. If you switch to a two-dimensional array, each line represents a number of coins, such as 15 lines (example in code, example is self-compiled) 1, 1, 1, 2, 2, 2, 5, 5, 10, 10, 10, 10, 10, 10, 20 for each line, which represents the denomination of the coin to be compact, and finally, if you construct an optimal solution, it will be the same as the backpack problem. The last line, or DP array here, ends up with a par value (from 0 to m), the number of coins needed, and of course, if the value is infinite, there is no solution. If I also want m-1, I can output dp[m-1] directly without moving anywhere else.

About the greedy algorithm: Of course, this topic can be solved using the greedy algorithm, and is simpler, but using the greedy algorithm to prove the correctness of the solution, specific will learn immediately, because you see greed in advance, so give the greedy algorithm code (easy to understand).

Some thought: In the end I kept thinking: If there is more than one item in the 01 backpack problem? If the backpack must be full? If the coin problem finishes with a corresponding number of coins used, it will be more meaningful to have a smaller number. A value description is that a smaller number represents a larger value. If so? If the coin problem changes to the minimum number of coins when the smallest number of coins is used to compose a value less than m and closest to m? If coins of different denominations have different weights, do you require the total weight of the final compact to be less than one value? Wait a moment, if you consider these if, then the three questions this time are, because the backpack must be full and the space can be fully utilized, so it is correct to use the greedy strategy (to prove it), and the coin problem is not the case where the backpack must be full? Of course, in this experiment, I have a lot of such thinking, perhaps because the dynamic planning problems meet those two characteristics, there will always be some similarity. These thoughts were just a flash of light in solving these questions, but they have been on my mind for a long time. I think they are meaningful, and I don't think the questions are fundamentally different this time. (Unlike the minimum editing problem and the longest common subsequence problem, although recursive, the nature of thinking is different)

Job summary: This job is completed after the corresponding experiment report, at this time, there is a lot of confidence in trying to complete these questions by yourself. When I finish my homework, I think for myself as much as possible and try to be clear (because true mastery is what needs to be said, which is important). While trying to be clear, I try to avoid writing too much. Of course, there are still many imperfections because it is a beginner. This assignment, after experimentation, has once again consolidated my understanding of dynamic planning, and I believe that if in the future I need to solve problems using dynamic planning or encounter problems using dynamic planning, I can cope with them. I've been working hard to learn algorithms better, but I always feel that I'm far behind. I hope I can really master algorithms one day.