CHAPTER_6 C++STL correlation

6.3 string

In the c language, we use char arrays to store strings, which can be cumbersome. Therefore, adding a string type to STL makes it easier for us to manipulate strings. To use a string, you need to add a header file #include <string>.

string's usage is recorded in Algorithmic Notes P202-P209. More detailed usage can be found in the blog Use of string in c+ _I'm a little leaf blog-CSDN blog_c++string usage.

Let's look at a topic to familiarize ourselves with string usage.

Title:

Give two numbers, write them in the form of scientific counting (reserving N-bit decimals), and ask them if they are equal. If they are equal, output YES and give the result of the conversion. If not, output NO and give the result of the conversion of two numbers.

Input Sample 1:

3 12300 12308.9

Output Sample 1:

YES 1.23*10^4

Input Sample 2:

3 120 128

Output Sample 2:

NO 1.200*10^2 1.280*10^2

Ideas:

We use string to read in two numbers to make it easier to manipulate the numbers. Considering the data itself, there are two situations in which we read in numbers: (1)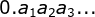 (2)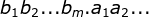That is, it is classified by whether the integer part is 0 or not.

First, we have to solve a small problem: Remove the leading 0 of the number. For example, enter it as 000.123 or 0012.3. First, we need to remove the excess 0 from the front so that the latter can be treated uniformly. The simple way to remove the leading 0 is to use the erase() method of the string class.

Scientific counting represents numbers as two parts: the floating-point part and the exponential part of 10. If the floating-point part and the exponential part are equal, then they are identified as equal YES. Conversely, they are not equal NO. For (1) (2) cases, we discuss the definition of their floating-point and exponential parts respectively. For discussion purposes, we assume that a three-digit decimal number, N=3, is preserved.

Situation (1)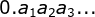First we find the first non-zero number after the decimal point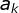When found, our exponent e is also determined, e=-k. For example, 0.0012, the first non-zero number is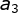Then the exponential part e=-3. e is actually the number of middle zeros plus one, and then the opposite number.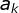After that, add a decimal point to the back, and then 3 digits back to make up the decimal part. If there are less than 3 digits behind, make up the insufficient digits by 0. For example, 0.0012 is made up by 1.200.

However, in case (1), there is another possibility that we did not consider: if we could not find the first non-zero number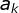What about? For example, 0.000 decimal points are all followed by 0. This is handled as follows: When the number is traversed, it is not found.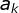When we truncate directly from the fourth digit after the original decimal point (that is, keep 3 digits), we get its floating point part. Obviously, the exponential Part e=0.

Situation (2)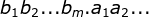After removing the leading 0, the first number 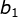Must not be 0. The exponential part is the total number of digits before the original decimal point minus one, that is, m-1. The floating point part is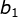Add the last three digits and make up for 0 if the number of digits is insufficient. For example, 123.4, exponent e=3-1=2, and floating-point part 1.234.

In case (2), there is also a special case: how do we determine the exponent e if the number has no decimal point? For example, 123000. Simply, an exponent minus one for the total number of digits, which is also m-1.

In summary, we have been able to categorize the two cases. So we need the last step: to determine if the number is case 1 or case 2. This is obviously not difficult. After we remove the leading 0, if the first decimal point is case 1 and vice versa, case 2.

Reference code:

#include<iostream>
#include<string>

using namespace std;

int n;                                   //Reserve n-digits 

void deal(string s,string &f,int &e) {
	int k,flag=0;
	while(s.size()>1&&s[0]=='0') {       //Remove leading 0 
		s.erase(0,1);
	}
	if(s=="0") {         	            //After removing the lead, a situation may occur, leaving only 
		f="0."+string(n,'0');           //A 0, which handles this case separately here 
		e=0;
		return;
	}
	if(s[0]=='.') {                     //Situation (1) 
		for(k=1;k<s.size();k++) {       //I Start from 1, skip s[0] which i s the decimal point 
			if(s[k]!='0') {
				flag=1;
				break;
			}
		}
		if(flag==0) {              //0 after the decimal point 
			f="0."+string(n,'0');
			e=0;
			return;
		}
		else {                          //The first non-zero number after the decimal point has been found 
			e=-k;
			s.insert(k+1,".");          //Insert decimal point after first non-zero number
			f=s.substr(k,2);
			k=k+2;                      //Include the first zero and decimal points in the f-string, k moves 2 bits backward 
			while(f.size()<n+2&&k<s.size()) {    //Start traversing the numbers after the decimal point and add them to the floating-point part 
				f.insert(f.end(),s[k]);          //Add s[i] to the end of f
				k++;
			}
			if(f.size()<n+2)                     //If the length is not enough, add 0 to the n decimal 
				f=f+string(n+2-f.size(),'0');
			return; 
		}
	}
	if(s[0]!='.') {                     //Situation (2) 
		for(k=0;k<s.size();k++) {       //Traverse a string from the beginning 
			if(s[k]=='.') {
				flag=1;
				break;
			}
		}
		if(flag==1) {                   //Find decimal point 
			e=k-1;
			f=s.substr(0,1)+"."; 	             //Counts the first number and decimal point into the f-string
			s.erase(k,1);
			k=1;                                 //Remove the decimal point and point k to the second element 
			while(f.size()<n+2&&k<s.size()) {    //Traverse from the second number and add them to the floating-point part 
				f.insert(f.end(),s[k]);          //Add s[i] to the end of f
				k++;
			}
			if(f.size()<n+2)                     //If the length is not enough, add 0 to the n decimal 
				f=f+string(n+2-f.size(),'0');
			return; 			 
		}
		else {                          //No decimal point 
			e=s.size()-1;
			f=s.substr(0,1)+"."; 	             //Counts the first number and decimal point into the f-string
			k=1;                                 //Point k to the second element 
			while(f.size()<n+2&&k<s.size()) {    //Traverse from the second number and add them to the floating-point part 
				f.insert(f.end(),s[k]);          //Add s[i] to the end of f
				k++;
			}
			if(f.size()<n+2)                     //If the length is not enough, add 0 to the n decimal 
				f=f+string(n+2-f.size(),'0');
			return; 			
		}
	}
	
}

int main() {
	int e1,e2;                 //e1, e2 hold the exponential part of two numbers 
	string s1,s2,f1,f2;        //f1, f2 hold the floating point portion of two numbers 
	cin>>n>>s1>>s2;
	deal(s1,f1,e1);
	deal(s2,f2,e2);
	if(f1==f2&&e1==e2)
		cout<<"YES "<<f1<<"*10^"<<e1<<endl;
	else
		cout<<"NO "<<f1<<"*10^"<<e1<<" "<<f2<<"*10^"<<e2<<endl;		
	return 0;
}