Backtracking algorithm
Backtracking is actually a search attempt process similar to enumeration. It is mainly to find the solution of the problem in the search attempt process. When it is found that the solution conditions have not been met, it will "backtrack" and try other paths. Backtracking is a search method of selecting the best, which searches forward according to the conditions of selecting the best to achieve the goal. However, when a certain step is explored, it is found that the original choice is not optimal or fails to reach the goal, so it is necessary to go back one step and make a new choice. This technique is called backtracking method, and the point satisfying the backtracking condition is called "backtracking point".
After all, in fact, the backtracking algorithm is an N-tree's pre order traversal plus post order traversal.
//Binary tree traversal framework func traverse(root) { if root is nil { return } //Preamble traversal code traverse(root.left) //Middle order traversal code traverse(root.right) //Sequential traversal code } //N-tree traversal framework func traverse(root) { if root is nil { return } for child := range root.children { //Preamble traversal code traverse(child) //Sequential traversal code } }
Backtracking framework
Backtracking algorithm is the traversal of N-tree, which is equal to the total number of currently available choices. At the same time, make the current choice at the location of the previous traversal (choose process), then start the recursion, and finally cancel the current choice at the location of the later traversal (choose process). The pseudo code is as follows:
/** * choiceList: Currently available selection list * track : It can be understood as a decision path, that is, a series of choices have been made * answer : Used to store the decision path that we meet the conditions */ func backtrack(choiceList, track, answer) { if track is OK { answer.add(track) } else { for choice as range choiceList { // choose: select a choice to join the track backtrack(choices, track, answer) // Uncheck: undo the above selection from track } } }
It can be seen that the core of the backtracking algorithm is actually the traversal of an N-tree. The backtracking algorithm is equivalent to a decision-making process, recursively traversing a decision tree, exhausting all decisions, and picking out the qualified decisions at the same time.
An example
If you want to eat, but where do you want to eat? What do you want to eat? This is a decision-making issue.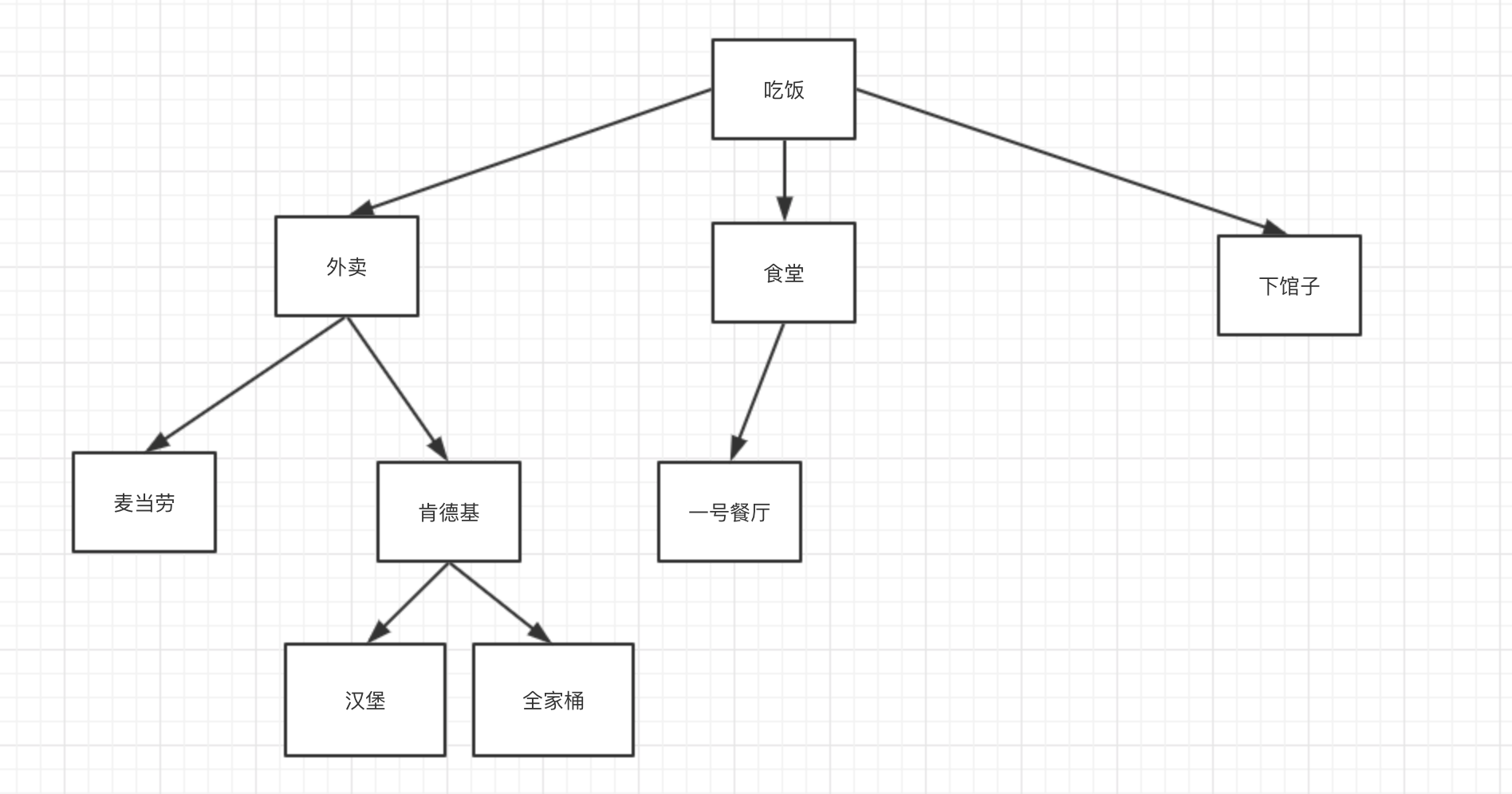
So how will computers choose? The way for computers to deal with problems is to exhaust. Here, computers will exhaust and compare all the decisions, and then choose an optimal strategy, such as: eat meal, take out, KFC, family bucket.
How to make the computer exhaust and compare all the decisions correctly is the design skill of backtracking algorithm. The core of backtracking algorithm is how to design the logic of choose and uncheck.
Permutation problem
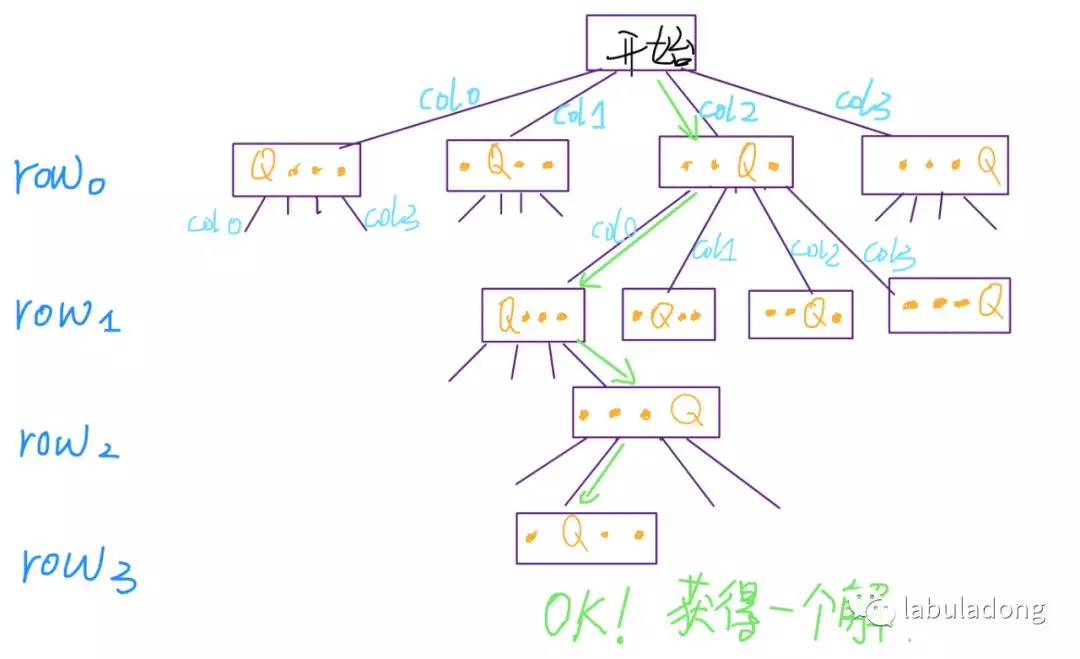
The total permutation problem is a typical backtracking algorithm problem. Our idea is to fix the first number as 1, then arrange 2 and 3 in full; then fix the first number as 2, arrange 1 and 3 in full; then fix the first number as 3, arrange 1 and 2 in full. This is a decision-making process. It is transformed into a decision tree to represent: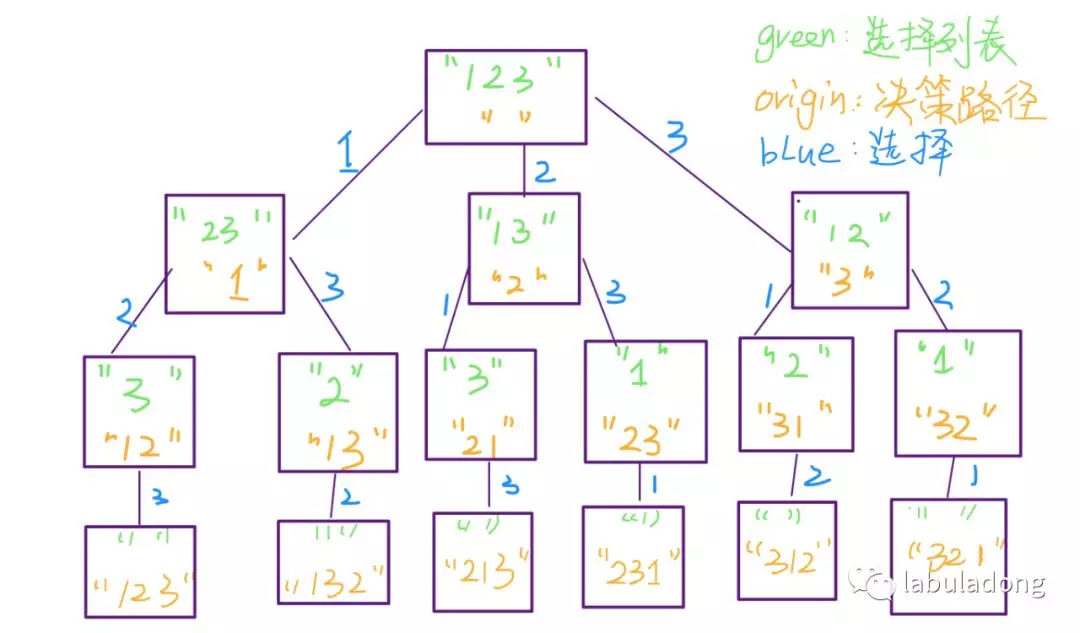
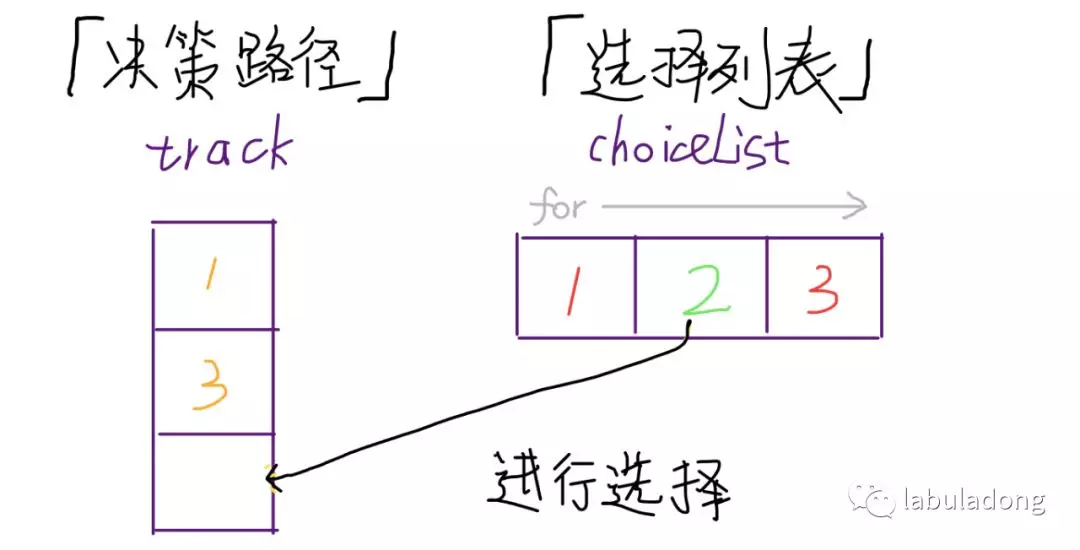
It can be found that each level down is to select a "choice" in the "selection list" to add "decision path", and then delete this choice from the "selection list" (to avoid repeated selection later); when a decision branch exploration is completed, we need to backtrack up, take the "choice" of the branch from the "decision list", and then take this "choice" Rejoin the selection list (for use by other decision branches).
The above is the process of choose and unchoose in the template. The choose process is to explore down and make a choice. The unchoose process is to backtrack up and undo the just choice.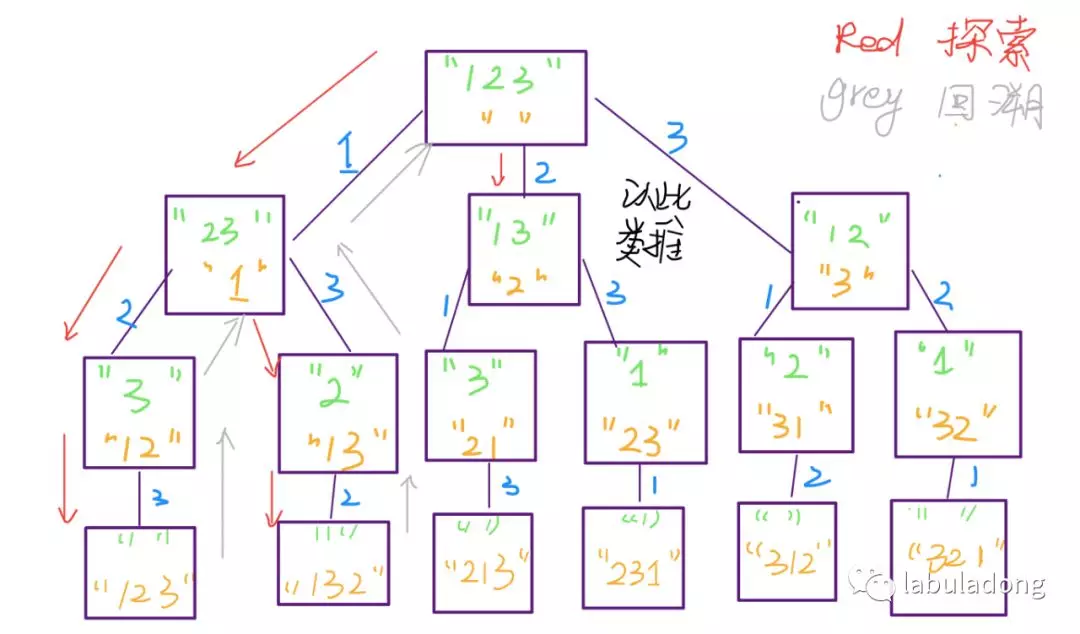
Now we can specify the template of backtracking algorithm for the problem of Full Permutation:
/** * choiceList: Selection list, currently available selection list * track : Decision path, a series of choices have been made * answer : Used to store the complete permutation */ func backtrack(choiceList, track, answer) { if track is OK { answer.add(track) } else { for choice as range choiceList { // choose process // Add choice to track // Move choice out of choiceList backtrack(choices, track, answer) // unchoose process // Move the choice out of the track // Add the choice back to the choiceList } } }
Here is the specific code (golang):
func permute(nums []int) [][]int { track := []int{} ans := [][]int{} backTrack(nums, &track, &ans) return ans } func backTrack(nums []int, track *[]int, ans *[][]int) { if len(*track) == len(nums) { tmp := make([]int, len(*track)) copy(tmp, *track) *ans = append(*ans, tmp) } else { for _, v := range nums { if isIn(v, *track) { continue } *track = append(*track, v) backTrack(nums, track, ans) *track = (*track)[:len(*track)-1] } } } func isIn(i int, arr []int) bool { for _, v := range arr { if v == i { return true } } return false }
N-queens problem

It is also the idea of backtracking. The code is as follows:
func solveNQueens(n int) [][]string { board := []string{} ans := [][]string{} initBoard(&board, n) backTrack(0, n, &board, &ans) return ans } //Initialize chessboard func initBoard(board *[]string, n int) { var s string for i := 0; i < n; i++ { s += "." } for i := 0; i < n; i++ { *board = append(*board, s) } } func backTrack(row int, n int, board *[]string, ans *[][]string) { if row == len(*board) { tmp := make([]string, len(*board)) copy(tmp, *board) *ans = append(*ans, tmp) } else { for col := 0; col < n; col++ { //If you choose this location, you will be attacked. Skip this location if !isPlace(board, row, col, n) { continue } //choose process (*board)[row] = strRex((*board)[row], col, 'Q') //Select next line backTrack(row + 1, n, board, ans) //unchoose process (*board)[row] = strRex((*board)[row], col, '.') } } } func strRex(s string, i int, b byte) string { bytes := []byte(s) bytes[i] = b s = string(bytes) return s } //Judge whether board[row][col] can place Q func isPlace(board *[]string, row, col, n int) bool { //Check directly above for i := 0; i < row; i++ { if (*board)[i][col] == byte('Q') { return false } } //Check upper right skew for i, j := row - 1, col + 1; i >= 0 && j < n; i, j = i-1, j+1 { if (*board)[i][j] == byte('Q') { return false } } //Check upper left skew for i, j := row - 1, col - 1; i >= 0 && j >= 0; i, j = i-1, j-1 { if (*board)[i][j] == byte('Q') { return false } } //No need to check the bottom, because there is no queen under return true }
"Decision path": board. Every step of decision-making is every line of board. row variable records the step of current decision-making path.
"Selection list": for a given row (i.e. every step in the decision-making), each column may be placed with a "Q", which is all the choices. The for loop in the code is to exhaust the "selection list" to determine whether the queen can be placed.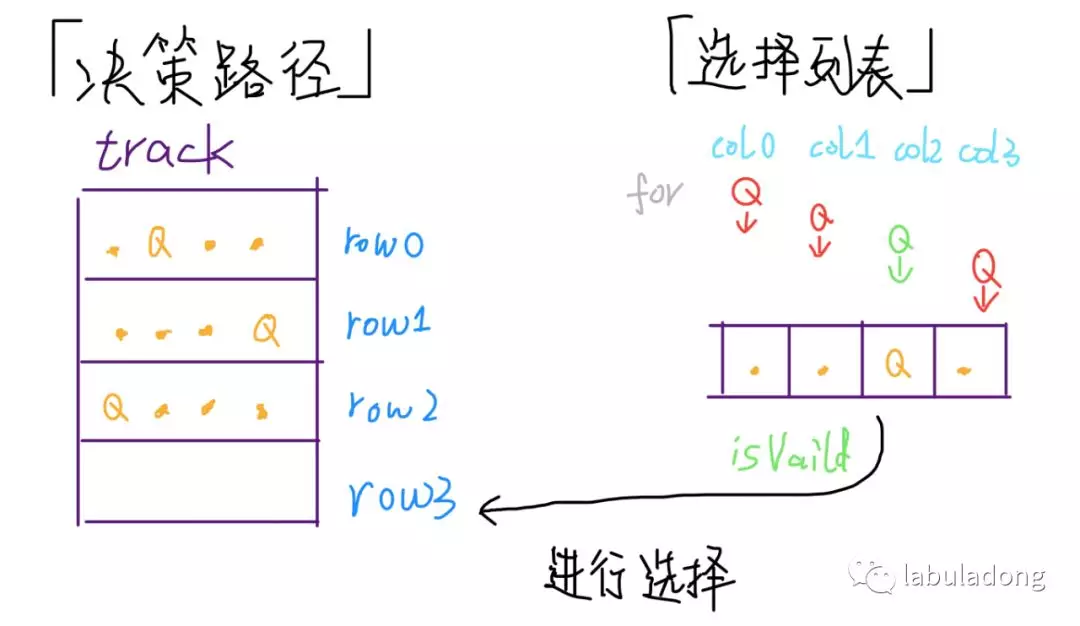
summary
Review the algorithm framework of backtracking
func backtrack(choiceList, track, answer) { if track is OK { answer.add(track) } else { for choice as range choiceList { // choose: select a choice to join the track backtrack(choices, track, answer) // Uncheck: undo the above selection from track } } }

