• Weighted Directed Graph
• data structure
  • Weighted Directed Edge
  • Weighted Directed Graph
  • Shortest path
• Edge Relaxation
• Dijkstra algorithm

Maps or navigation systems are typical applications of shortest paths, where vertices correspond to intersections, edges correspond to highways, and edge weights correspond to the cost (time or distance) of a journey.In this model, the problem can be summarized as finding the least costly path from one vertex to another.In addition, network routing and task scheduling are similar problems.

Weighted Directed Graph

The weighted directed graph is a model for studying the shortest path problem.In a weighted directed graph, each directed edge has a weight associated with it. The weight of a path refers to the sum of the weights of all the edges on the path. So in a weighted directed graph, the problem of finding the shortest path from vertex v to w becomes the least weight among all the paths from vertex v to W.

data structure

Weighted Directed Edge

Weighted directed edges are the basic elements that make up a weighted directed graph, and have start, end, and weight attributes.

public class DirectedEdge {
    private final int v; 
    private final int w; 
    private final double weight; 

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public double weight() {
        return this.weight;
    }

    public int from() {
        return this.v;
    }

    public int to() {
        return this.w;
    }

    public String toString() {
        return String.format("%d->%d %.2f", v, w, weight);
    }
}

Weighted Directed Graph

In the data structure of a weighted directed graph, the weighted directed edges are organized similarly to those of a previous directed graph, except in the adjacency table, where the vertices of the graph were previously stored and the edges are now stored.

public class EdgeWeightedDigraph {
    private static final String NEWLINE = System.getProperty("line.separator");
    private final int V; // vertex
    private int E; // edge
    private Bag<DirectedEdge>[] adj;

    public EdgeWeightedDigraph(int V) {
        this.V = V;
        this.E = 0;
        adj = (Bag<DirectedEdge>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<DirectedEdge>();
        }
    }

    public EdgeWeightedDigraph(In in) {
        this(in.readInt());
        int E = in.readInt();
        for (int i = 0; i < E; i++) {
            int v = in.readInt();
            int w = in.readInt();
            double weight = in.readDouble();
            DirectedEdge e = new DirectedEdge(v, w, weight);
            addEdge(e);
        }
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }

    public void addEdge(DirectedEdge e) {
        adj[e.from()].add(e);
        E++;
    }

    public Iterable<DirectedEdge> adj(int v) {
        return adj[v];
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " vertices, " + E + " edges " + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (DirectedEdge w : adj[v]) {
                s.append(w + " | ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }

    public Bag<DirectedEdge> edges() {
        Bag<DirectedEdge> b = new Bag<DirectedEdge>();
        for (int v = 0; v < V; v++) {
            for (DirectedEdge w : adj[v]) {
                b.add(w);
            }
        }
        return b;
    }
}

Shortest path

When calculating the shortest path in a weighted directed graph, an array of DirectedEdge objects, edgeTo[], and an array of double type, distTo[], are used.

• EdTo represents a shortest path tree and stores the results of the algorithm.A shortest path tree starting with s is a subgraph of the graph, which contains s and all vertices reachable from S.The root node of this tree is s, and each path of the tree is a shortest path in the directed graph. The index of edgeTo denotes the node of the graph, and the value of edgeTo[4] points to the edge of node 4, which is to=4, from=points to the vertex of node 4, and weight=the weight of the edge. According to edgeTo, the shortest path tree can be traced up to its root node s.The value of edgeTo[s] is null.

• DistTo[] stores the cost of the shortest path from one node to the starting point s.So distTo[s]=0, and it is agreed that for nodes that are not connected to s, the value of the corresponding location in distTo is Double.POSITIVE_INFINITY, so that if a distTo location is equal to Double.POSITIVE_INFINITY, you can know if it is connected to s.

Edge Relaxation

The implementation of the shortest path algorithm is based on a simple operation called relaxation.At first, only the edges of the graph and their weights are known. Only the elements corresponding to the starting point in distTo[] have a value of 0. The values of the remaining elements are initialized to Double.POSITIVE_INFINITY. As the algorithm executes, it stores the shortest path information from the starting point to other vertices in edgeTo[] and distTo[].When new edges are encountered, the shortest path is updated by relaxation.Relaxation means that for edge v->w, the shortest path from s to w will be checked to see if it passes v, i.e., s->v->w. If so, the edgeTo[w] and distTo[w] will be updated, otherwise the status quo will be maintained.

if (distTo[w] > distTo[v] + e.weight()) {
	distTo[w] = distTo[v] + e.weight();
	edgeTo[w] = e;
}

The term relaxation comes from the analogy of using a rubber band to spread tightly along a path connecting two points. Relaxing an edge is like transferring a rubber band to a shorter path to make it relax compared to before.

In the implementation of the shortest path algorithm, all edges pointed out from one vertex are attempted to relax. If a relaxation operation changes the values of distTo and edgeTo, the operation is successful and the shortest path to each vertex is eventually found.

Dijkstra algorithm

The Dijkstra algorithm is based on the discussion above and requires an index priority queue (IndexMinPQ) in addition to the distTo and edgeTo arrays to hold the vertices that need to be relaxed and confirm the next one.IndexMinPQ not only has the function of MinPQ, but also can modify the value of corresponding location by index. The algorithm uses IndexMinPQ to associate vertex v with distTo[v], and sets corresponding path distance according to index in relaxation operation.

public class DijkstraSP {
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    private IndexMinPQ<Double> pq;
    int s;

    public DijkstraSP(EdgeWeightedDigraph G, int s) {
        edgeTo = new DirectedEdge[G.V()];
        distTo = new double[G.V()];
        pq = new IndexMinPQ<Double>(G.V());
        this.s = s;

        for (int v = 0; v < G.V(); v++) {
            distTo[v] = Double.POSITIVE_INFINITY;
        }

        distTo[s] = 0.0;
        pq.insert(s, 0.0);
        while (!pq.isEmpty()) {
            relax(G, pq.delMin());
        }
    }

    private void relax(EdgeWeightedDigraph G, int v) {
        for (DirectedEdge e : G.adj(v)) {
            int w = e.to();
            if (distTo[w] > distTo[v] + e.weight()) {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
                if (pq.contains(w))
                    pq.change(w, distTo[w]);
                else
                    pq.insert(w, distTo[w]);
            }
        }
    }

    public double distTo(int w) {
        return distTo[w];
    }

    public boolean hasPathTo(int w) {
        return distTo(w) < Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v) {
        if (!hasPathTo(v))
            return null;

        Stack<DirectedEdge> path = new Stack<DirectedEdge>();
        for (DirectedEdge a = edgeTo[v]; a != null; a = edgeTo[a.from()]) {
            path.push(a);
        }
        return path;
    }

    // cmd /c --% java algs4.four.DijkstraSP ..\..\..\algs4-data\tinyEWG.txt
    public static void main(String[] args) {
        In in = new In(args[0]);
        EdgeWeightedDigraph ewdg = new EdgeWeightedDigraph(in);
        int s = Integer.parseInt(args[1]);
        DijkstraSP dijkstraSP = new DijkstraSP(ewdg, s);

        for (int t = 0; t < ewdg.V(); t++) {
            StdOut.print(s + " to " + t);
            StdOut.printf(" (%4.2f): ", dijkstraSP.distTo(t));
            if (dijkstraSP.hasPathTo(t)) {
                for (DirectedEdge e : dijkstraSP.pathTo(t)) {
                    StdOut.print(e + " ");
                }
            }
            StdOut.println();
        }
    }
}

8
16
4 5 0.35
4 7 0.37
5 7 0.28
0 7 0.16
1 5 0.32
0 4 0.38
2 3 0.17
1 7 0.19
0 2 0.26
1 2 0.36
1 3 0.29
2 7 0.34
6 2 0.40
3 6 0.52
6 0 0.58
6 4 0.93

For the graph specified in tinyEWG.txt above, if you want to calculate the shortest path from each point to starting point 0, the algorithm's execution path is:

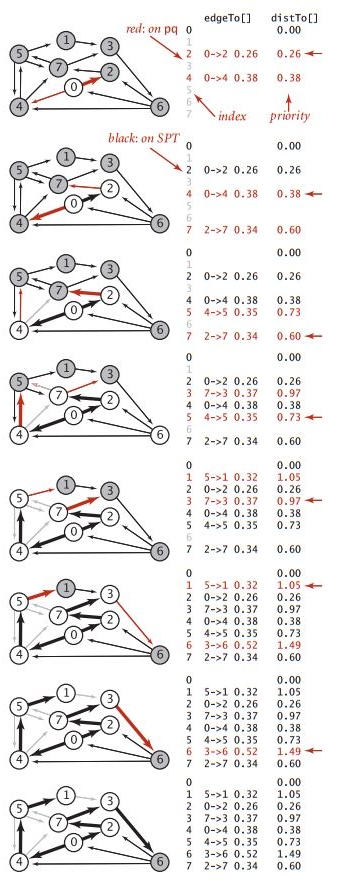
• Add vertex 0 to the priority queue, relax the edge starting with vertex 0, add vertices 2 and 4 pointing from 0 to the priority queue, and add edges 0_>2 and 0->4 to the tree.
• Remove vertex 2 from the priority queue, add 2->7 to the tree, and add vertex 7 to the priority queue.
• Remove vertex 4 from the priority queue and add 4->5 to the tree, but because 4->7 relaxation failed, this edge failed and vertex 5 was added to the priority queue;
• Remove vertex 7 from the priority queue, add 7->3 to the tree, 7->5 relaxation fails, and add vertex 3 to the priority queue.
• Remove vertex 5 from the priority queue, add 5->1 to the tree, 5->7 relaxation fails, and add vertex 5 to the priority queue.
• Remove vertex 3 from the priority queue, add 3->6 to the tree, and add vertex 6 to the priority queue.
• Remove vertex 6 from the priority queue, the priority queue is empty, and the execution is complete.