KMP algorithm: an improved string matching algorithm

Solve the original problem: str1 and str2 are two strings, and whether a substring in str1 is equal to str2

In Java, the getIndexOf (str1, str2) method of String is whether str2 is included in str1, which returns true, not false. In fact, KMP algorithm is used in the middle.

Violence algorithm: match str1 from the beginning. If the first one matches the first one in str2, then compare it downward. If not, then compare str2's first item with str1's next position. Complexity O(n*m)

KMP process introduction:

In a string, the matching length of the longest prefix and the longest suffix before a character is used to simplify the solution.
(neither prefix nor suffix can take all the length before the character. len<qian.length-1)

This information is that for each element T j of each pattern string t, there is a real number k, which makes the K characters (t0t1 t k-1) is followed by K (t j-k tj-k + 1) in front of TJ t j-1, where the first character t j-k starts from t 1 at most, so K < j) characters are the same. If there are more than one such K, take the largest one. The character of each position j in pattern string t has this information, which is represented by next array, that is, next [j] = max {K}. Note: by default, next is - 1 at 0 and 0 at 1.

1. First, find out the information of str2: generate the next array of shaping, and return the matching length of the longest prefix and the longest suffix at each position. For example, in the str2 of ababac, the next array is [- 1 0 1 2 3]. Then the next array is used to guide the subsequent matching.
2. Examples are as follows:
   A segment string is a prefix of f.
   Segment B string is a suffix of f.
   Segment A string is equal to segment B string.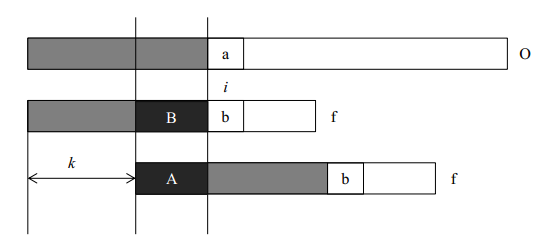
   
   3. By using the matching length, a position in str2 corresponds to the starting position in str2, and then find the j position in str1 in sequence. At this time, the head of str2 moves to the beginning of the longest suffix, and then start matching from the j position. If the j position still does not match, then continue to find the longest prefix and suffix in str2 relay at this time, and str2 continues to move backward.

The content of this algorithm process simplification:

It is clear that in a comparison, the positions from i at the beginning of str1 to j in the middle do not match with str2. At this time, these positions in the middle will not be judged, saving time.

public static int getIndexOf(String s,String m){
	if(s == null || m == null ||m.length()<1 ||s.length<m.length){
		return -1;
	}
	//Here are all the steps of KMP algorithm
	char[] str1 = s.toCharArray();
	char[] str2 = m.toCharArray();
	int i1 = 0;
	int i2 = 0;
	//Matching array
	int[] next = getNextArray(str2);
	while(i1<str1.length && i2<str2.length){
		if(str1[i1] == str[i2]){
			i1++;
			i2++;
		//-1 is the starting position
		}else if(next[i2] == -1){
			i1++;
	    //At this time, i1 has reached different positions
	    //In this case, let i2 directly cross the matching part, starting from different positions
		}else{
			i2 = next[i2]; 
			//Notice that str2 starts from 0,
			//So str[i2] returned is exactly the last number of the longest prefix
		}
	}
	//If i2 slips to the end, then the proof is found. If it doesn't equal to i2 at the end, then it returns negative one, not found
	return i2 = str2.length ? i1-i2:-1;

getNext function: longest prefix and suffix matching length solution

1. First determine the matching length L at the ith position
2. When judging the matching length of the i+1 position, it is necessary to judge the next character of the first half A in the matching length of the i position and compare it with the character of the i position
3. If equal, the matching length of the i+1 position is L+1
4. If not, read out the matching length of the first half A, divide the first half B of A, and then return to step 2 for judgment.
5. The last half contains only the first character of the whole string. If it is not equal at this time, it returns 0, and if it is equal, it returns 1.
   [a good stroke]
   The code is as follows:

public static int[] getNextArray(char[] str2){
	if(str2.length == 1){
		return new int[] {-1};
	}
	int[] next = new int[str2.length];
	next[0] = -1;
	next[1] = 0;
	//i represents the starting position of the array
	int i = 2;
	//cn stands for matching length
	int cn = 0;
	while(i<next.length){
		//If equal, the matching length of the next character plus one
		if(str2[i-1] == str2[cn]){
			next[i++] = ++cn;
		//If they are not equal, then the matching length becomes the matching length value at cn,
		//Then repeat the whole while loop, and judge again. At this time, the value of i will not change,
		//It will judge all the time, until the last cn=0, let the matching length be 0, and make the next judgment.
		}else if(cn>0){
			cn = next[cn];
		}else{
			next[i++] = 0;
		}
	}
	return next;
}

Related topics in recent years:

1. [JD] given a string, it is required to add the shortest character after it to generate a new string containing two original strings.
[idea] after calculating the matching length of the longest prefix and suffix of the string, the next array can find one more bit to get the longest prefix and suffix. Then the second string only needs to overlap the prefix with the suffix of the original string and complete the supplement.

2. How to judge whether a string is not obtained by a substring repeated many times
If it is obtained by the substring repeated many times, under the termination condition, each matching length is the corresponding increase number of the first matching length, and the array length is a multiple of the substring length, which has a relationship with the matching array. emmm only thought and found the original violent solution...

public class test0315 {
	public static void main(String[] args) {
		Solution S = new Solution();
		String s = "abababab";
		boolean a = S.repeatedSubstringPattern(s);
		System.out.println(a);
	}
}
 
class Solution {
    public boolean repeatedSubstringPattern(String s) {
        if (s == null || s.length() < 2) {
            return false;
        }
        int i = 1;
        while (i < s.length()) {
            if (s.length() % i == 0) {
            	//The total length of the string must be even,
                String temp = s.substring(0, i);
               //Compare the first i-bit characters as a whole with the following i-bit characters each time
                int j = i, k = j + i;
                while (k <= s.length()) {
                    if (!s.substring(j, k).equals(temp)) {//
                        break;
                    }
                    //Add i digit each time
                    j += i;
                    k += i;
                }
                if (k > s.length()) {
                    return true;
                }
            }
            i++;
        }
        return false;
    }
}