array
Because the array has subscripts, the query is fast. However, since the memory size has been set at the time of creation, it is troublesome to expand the capacity. It is necessary to copy the original array to a larger array.
Linked list
Each item in the linked list occupies its own memory. They do not exist in a piece of memory. Each item is linked by mutual reference.
Advantages: addition and deletion are very convenient, and the query is troublesome. You can only traverse from the head element.
Hash tables combine the two
Hash
Hash is also called hash and hash. The corresponding English is hash. The basic principle is to change the input of any length into the output of fixed length through hash algorithm. The mapping rule is the corresponding hash algorithm, and the binary string mapped by the original data is the hash value.
Features of Hash:
1. The original data cannot be deduced reversely from the hash value.
2. A small change in the input data will get a completely different hash value, and the same data will get the same value
3. The execution efficiency of hash algorithm should be efficient, and the hash value can be calculated quickly for long text.
4. The collision probability of hash algorithm is small.
The principle of hash is to map the value of input space into hash space, and the space of hash value is much smaller than the input space. According to the drawer principle, there must be cases where different inputs are mapped to the same output.
Drawer principle: there are ten apples on the table. Put these ten apples in nine drawers. No matter how you put them, we will find that there are at least two apples in at least one drawer.
One of the member variables of HashMap is Node
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
put principle
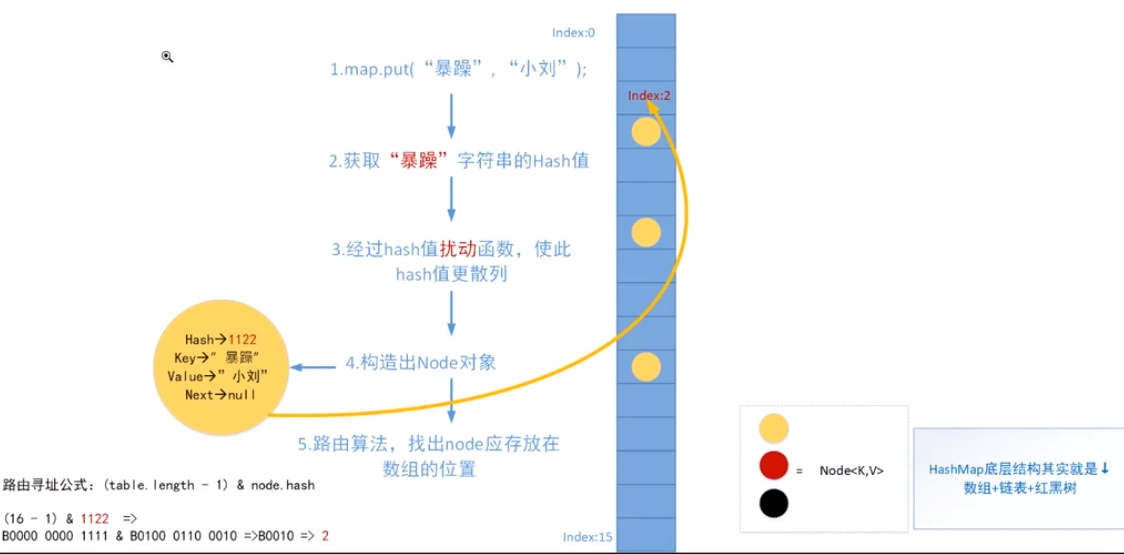
Routing addressing formula:
(table.length-1) & node.hash
First of all, table.length must be the power of 2, and after - 1, it must be all 1. For example, 15 is 1111 31 is 11111
This operation is actually equivalent to node.hash/table.length takes the remainder. Why should we take the remainder? In this way, we can ensure that the index obtained must be within the length of table.length.
Source code!!!
Let's start with a few constants
// The default array size is 16 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
// Maximum length of array static final int MAXIMUM_CAPACITY = 1 << 30;
// Default load factor static final float DEFAULT_LOAD_FACTOR = 0.75f;
// When the length of the linked list reaches 8, it will be upgraded to a tree static final int TREEIFY_THRESHOLD = 8;
// The tree is degraded to a linked list static final int UNTREEIFY_THRESHOLD = 6;
// The treelization is not allowed until the array reaches 64 static final int MIN_TREEIFY_CAPACITY = 64;
Look at the member variables
transient Node<K,V>[] table;
// Number of elements in the current hash table transient int size;
// Structure modification times in hash table transient int modCount;
// Capacity expansion threshold: trigger capacity expansion when the elements in your hash table exceed the threshold // Threshold = capacity (array length) * loadFactor int threshold;
// Load factor final float loadFactor;
Construction method:
public HashMap(int initialCapacity, float loadFactor) {
// Initialization array size cannot be less than 0
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
// The initialization array size cannot be greater than the maximum value
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
// The load factor cannot be less than 0 or non numeric
// NaN is actually short for Not a Number. The value of 0.0f/0.0f is NaN. Mathematically speaking, 0 / 0 is an unknown value
// determine.
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
// Function: returns a number greater than or equal to the current value cap, and this number must be to the power of 2.
// Assuming cap = 10, 16 should be returned
// cap = 10 , n = cap - 1 = 9,
// 0b1001 >>> 1 = 0b0100
// Both or below 0b1001 | 0b0100 = 0b1101
// 0b1101 | 0b0011 (after moving two bits to the right) = 0b1111 = 15
// 0b1111 | 0b0000 = 0b1111
// Then it's all the same
The last is 15+1 = 16
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}put method:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}The hash method was called first
// Function: let the upper 16 bits of the hash value of the key also participate in the routing operation
static final int hash(Object key) {
int h;
// When you put null, put it in bit 0
// Suppose h = 0b 0010 0101 1010 1100 0011 1111 0010 1110
// h >>> 16 = 0000 0000 0000 0000 0010 0101 1010 1100
// ^If different goods are the same, return 0 and if different, return 1
// The result is 0010 0101 1010 1100 0001 1010 1000 0010
// Why do you want to do this? If the table is very small, the high bit cannot participate in the operation when routing addressing
// If you move to the right, you can put the high-level ones in, which can reduce hash conflicts
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}Next, look at putVal()
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
// tab: hash table referencing the current hashMap
// p: Represents the element of the current hash table
// n: Represents the length of the hash table array
// i: Indicates the route addressing result
Node<K,V>[] tab; Node<K,V> p; int n, i;
// First copy, assign table to tab, and then assign the array length to n
// If table is equal to null or the array length is 0, it is initialized. The advantage of this is that it is initialized only when put, and the idea of lazy loading
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// (n-1) & hash is the routing addressing algorithm = = null, which means that the current node has no value, so put it directly.
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else { // Otherwise, it is found that there is already a value
// e: If it is not null, a key consistent with the key value to be inserted is found
// k: Represents a temporary key
Node<K,V> e; K k;
// If the currently inserted element is the same as the hash in the addressed array, assign p to temporary w
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}