Analytical normals 3D code analysis

Author: iq, website: https://www.shadertoy.com/view/XttSz2

label: 3d, noise, normals, analytical, numerical

A total of one part: Image

Camera settings

This is more common, that is, simple camera rotation and matrix acquisition

// camera anim
float an = 0.1*iTime;
vec3 ro = 3.0*vec3( cos(an), 0.8, sin(an) );
vec3 ta = vec3( 0.0 );
// camera matrix	
vec3  cw = normalize( ta-ro );
vec3  cu = normalize( cross(cw,vec3(0.0,1.0,0.0)) );
vec3  cv = normalize( cross(cu,cw) );
vec3  rd = normalize( p.x*cu + p.y*cv + 1.7*cw );

Intersection test function

Then the intersection test is carried out

vec4 interesect( in vec3 ro, in vec3 rd )
{
	vec4 res = vec4(-1.0);

    // Square intersection test   
    vec2 dis = iBox( ro, rd, vec3(1.5) ) ;
    if( dis.y<0.0 ) return res;

    // raymarch
    float tmax = dis.y;
    float t = dis.x;
	for( int i=0; i<128; i++ )
	{
        vec3 pos = ro + t*rd;
		vec4 hnor = map( pos );
        res = vec4(t,hnor.yzw);
        
		if( hnor.x<0.001 ) break;
		t += hnor.x;
        if( t>tmax ) break;
	}

	if( t>tmax ) res = vec4(-1.0);
	return res;
}

The first is judgment Does the ray intersect the square , if they intersect, return the two intersections. For details about intersection test functions, please refer to IQ blog. Then RayMarching is performed within the range of [tmin,tmax] generated by the two intersections. The core is the Map function, as shown below:

vec4 map( in vec3 p )
{
	vec4 d1 = fbmd( p );
    d1.x -= 0.37;
	d1.x *= 0.7;
    d1.yzw = normalize(d1.yzw);
    // clip to box
    vec4 d2 = sdBox( p, vec3(1.5) );
    return (d1.x>d2.x) ? d1 : d2;
}

Specific analysis: for d1, it is through Fractional Brownian function Obtain random points (where x component is t and yzw is normal). The difference between this and the FBM function known before is that the normal vector of random points is obtained. Of course, we can also directly use the conventional calNormal function. For the result, interval remapping is carried out. Why do you need this remapping (one addition, one subtraction, one multiplication)? Its core is addition and subtraction, and multiplication doesn't matter (the effect is the same). Imagine that if we don't subtract a value, the return value of FBM is always greater than 0. No matter how we move forward (on FMB, the performance is moving on the surface), it won't end. In the effect performance, if we delete this line, all rays will be cast to infinity, Increasing the subtraction value, the closer the geometry is to the complete square.

Then, when judging the distance from the square, the two results are compared to return the result with larger value and normal vector. Return to the intersect function, followed by the conventional ray stepping operation. Finally, return the main function.

Rendering process

First calculate AO. Use spherical Fibonacci sampling (actually hemisphere) to obtain uniform sampling. Sample 32 times, map each time, accumulate the step distance of the returned result, and then divide by 32. There is a problem here - multiply 3 and 5 respectively during Clamp. Analysis here: because our judgment on the sampling point is its distance from the geometry, not the depth map of the light direction, even for the points on the surface of the cube, their return value will not be very large, so we need to multiply it by multiple.

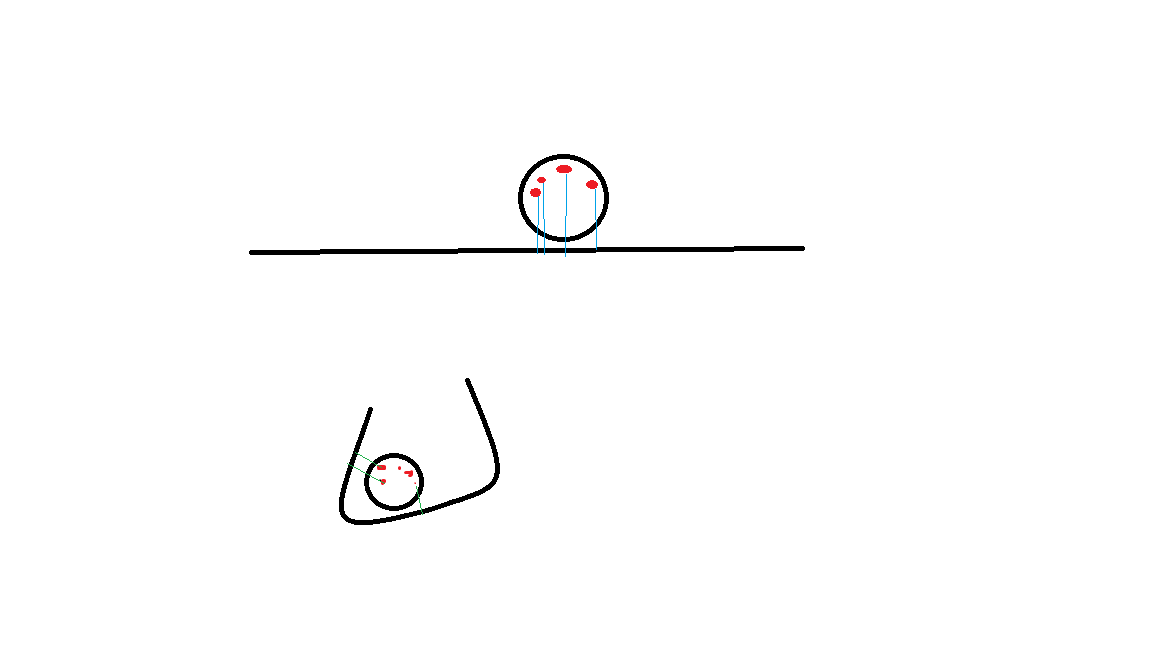
float calcAO( in vec3 pos, in vec3 nor )
{
	float ao = 0.0;
    for( int i=0; i<32; i++ )
    {
        //Spherical Fibonacci uniform sampling
        vec3 ap = forwardSF( float(i), 32.0 );
        //Random value
        float h = hash(float(i));
        //Reverse normal direction hemisphere reverse direction
		ap *= sign( dot(ap,nor) ) * h*0.25;
        ao += clamp( map( pos + nor*0.001 + ap ).x*3.0, 0.0, 1.0 );
    }
	ao /= 32.0;
	
    return clamp( ao*5.0, 0.0, 1.0 );
}

Then calculate Fre, Fro.

float fre = clamp( 1.0+dot(rd,nor), 0.0, 1.0 );
float fro = clamp( dot(nor,-rd), 0.0, 1.0 );

Among them, Fre is the approximation of the Fresnel effect, which is roughly shown in the figure: in the figure, the more flat, the shorter the purple segment, the greater the value of 1 minus the purple segment, the stronger the Fresnel effect. Fro is the opposite, or close to the general calculation.

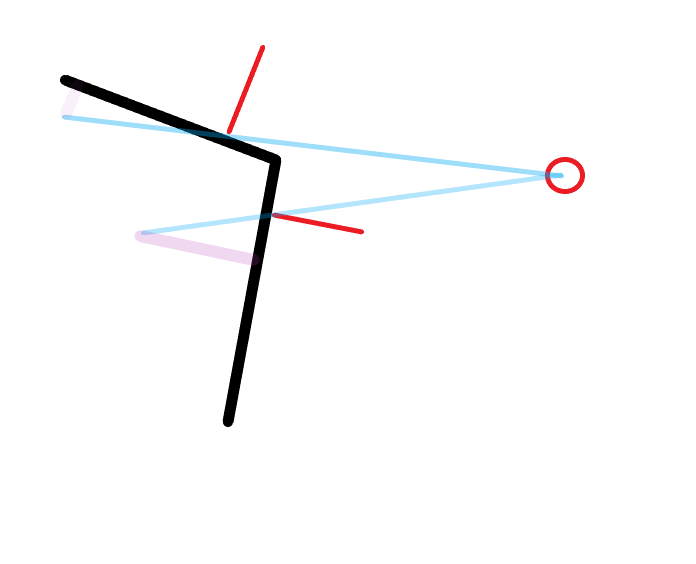
Then formally calculate the color

col = mix( vec3(0.05,0.2,0.3), vec3(1.0,0.95,0.85), 0.5+0.5*nor.y );
//col = 0.5+0.5*nor;
col += 10.0*pow(fro,12.0)*(0.04+0.96*pow(fre,5.0));
col *= pow(vec3(occ),vec3(1.0,1.1,1.1) );

The first is the color of the hook, which will be related to the color of the line of people. The second line, use the calculated fre, fro. I don't know the specific meaning. I'll have a chance to understand it in the future. The third line, add AO.

Finally, after switching to gamma space, it ends.

*Tool iBox function

vec2 iBox( in vec3 ro, in vec3 rd, in vec3 rad ) 
{
    vec3 m = 1.0/rd;
    vec3 n = m*ro;
    vec3 k = abs(m)*rad;
    vec3 t1 = -n - k;
    vec3 t2 = -n + k;
	float tN = max( max( t1.x, t1.y ), t1.z );
	float tF = min( min( t2.x, t2.y ), t2.z );
	if( tN > tF || tF < 0.0) return vec2(-1.0);
	return vec2( tN, tF );
}

*Tool FBMD function

vec4 fbmd( in vec3 x )
{
    const float scale  = 1.5;

    float a = 0.0;
    float b = 0.5;
	float f = 1.0;
    vec3  d = vec3(0.0);
    for( int i=0; i<8; i++ )
    {
        vec4 n = noised(f*x*scale);
        a += b*n.x;           // accumulate values		
        d += b*n.yzw*f*scale; // accumulate derivatives
        b *= 0.5;             // amplitude decrease
        f *= 1.8;             // frequency increase
    }
	return vec4( a, d );
}

*Tool SdBox function

vec4 sdBox( vec3 p, vec3 b ) // distance and normal
{
    vec3 d = abs(p) - b;
    float x = min(max(d.x,max(d.y,d.z)),0.0) + length(max(d,0.0));
    vec3  n = step(d.yzx,d.xyz)*step(d.zxy,d.xyz)*sign(p);
    return vec4( x, n );
}

*Tool ValueNoise and its gradient

float hash( float n ) { return fract(sin(n)*753.5453123); }
vec4 noised( in vec3 x )
{
    vec3 p = floor(x);
    vec3 w = fract(x);
	vec3 u = w*w*(3.0-2.0*w);
    vec3 du = 6.0*w*(1.0-w);
    
    float n = p.x + p.y*157.0 + 113.0*p.z;
    
    float a = hash(n+  0.0);
    float b = hash(n+  1.0);
    float c = hash(n+157.0);
    float d = hash(n+158.0);
    float e = hash(n+113.0);
	float f = hash(n+114.0);
    float g = hash(n+270.0);
    float h = hash(n+271.0);
	
    float k0 =   a;
    float k1 =   b - a;
    float k2 =   c - a;
    float k3 =   e - a;
    float k4 =   a - b - c + d;
    float k5 =   a - c - e + g;
    float k6 =   a - b - e + f;
    float k7 = - a + b + c - d + e - f - g + h;

    return vec4( k0 + k1*u.x + k2*u.y + k3*u.z + k4*u.x*u.y + k5*u.y*u.z + k6*u.z*u.x + k7*u.x*u.y*u.z, 
                 du * (vec3(k1,k2,k3) + u.yzx*vec3(k4,k5,k6) + u.zxy*vec3(k6,k4,k5) + k7*u.yzx*u.zxy ));
}

return vec4( k0 + k1*u.x + k2*u.y + k3*u.z + k4*u.x*u.y + k5*u.y*u.z + k6*u.z*u.x + k7*u.x*u.y*u.z, 
             du * (vec3(k1,k2,k3) + u.yzx*vec3(k4,k5,k6) + u.zxy*vec3(k6,k4,k5) + k7*u.yzx*u.zxy ));

}

### *Tool ForwardSF function