catalogue
1. Definition of one-dimensional array
2. Definition of two-dimensional array
2. Storage mode of two-dimensional array
(2) priority storage mode by column
2. Definition of special matrix
3. Compressed storage of special matrix
1. Definition of sparse matrix
2. Storage mode of sparse matrix
3. Triple storage of sparse matrix
1, Definition of array
1. Definition of one-dimensional array
A finite sequence consisting of n (n > 1) data elements with the same properties. For example:
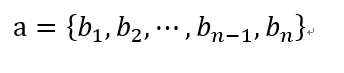
It is also a linear table in itself.
2. Definition of two-dimensional array
The array used to store arrays is called a two-dimensional array. Because the one-dimensional array is a linear table, the two-dimensional array can also be regarded as a linear table, and each data element is a linear table. Similar to a mathematical matrix. (see the basic introduction of other arrays.) Detailed introduction of array_ m0_50708613 blog - CSDN blog)
As shown in the figure: the two-dimensional array S is a matrix with m rows and n columns
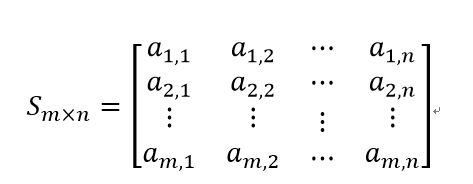
It is described in binary form as:

2, Storage structure of array
1. Array storage mode
The general array is stored in sequential storage structure. This has a great relationship with the one-dimensional structure of the memory storage unit.
2. Storage mode of two-dimensional array
There are two ways to store by two-dimensional row first and by two-dimensional column first.
(1) Priority storage by row
Let each element occupy k storage units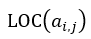 Represents the storage address of an element.
Represents the storage address of an element.

In C language, array subscripts start from 0
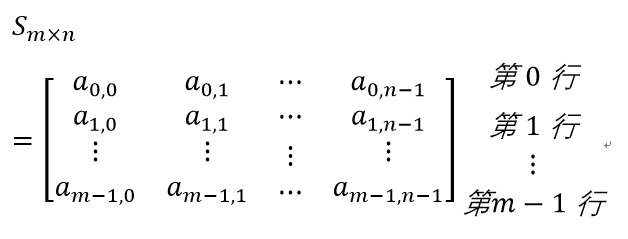
(2) priority storage mode by column
Let each element occupy k storage units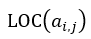 Represents the storage address of an element.
Represents the storage address of an element.


3, Matrix
1. Definition of matrix
A Matrix is a number table composed of m rows and n columns.
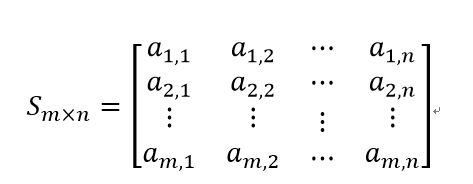
2. Definition of special matrix
Special matrix generally refers to the matrix with non-zero elements or certain regularity in the distribution of zero elements, also known as square matrix. There are symmetric matrix, orthogonal matrix, diagonal matrix and zero matrix, etc.
3. Compressed storage of special matrix
(1) Symmetric matrix
a: Definition of symmetric matrix
An n-order square matrix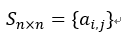 Elements in meet
Elements in meet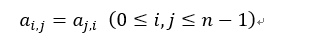 , called n-order symmetric matrix.
, called n-order symmetric matrix.
b: Storage of symmetric matrix
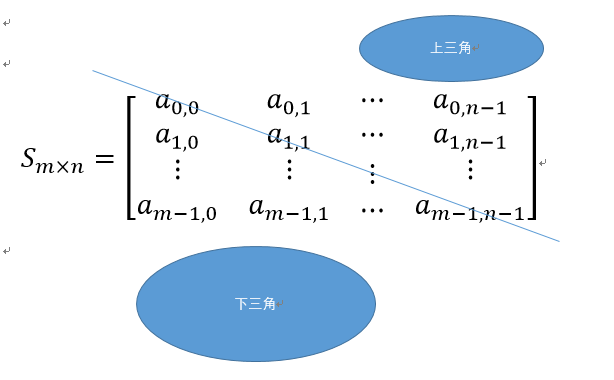
According to the characteristics of the symmetric matrix, the symmetric matrix is symmetrical along the main diagonal, so only some elements of the upper triangle or the lower triangle can be stored, and the originally stored n^2 elements are compressed and stored in the storage space of n (N1) / 2 elements. (similar to the distribution of 99 multiplication table)
4, Sparse matrix
1. Definition of sparse matrix
When the number of non-zero elements in the matrix is far less than the total number of elements of the matrix, it is called sparse matrix.
2. Storage mode of sparse matrix
Triple and cross linked list are two storage methods. The compressed storage method of sparse matrix stores only non-zero elements.
3. Triple storage of sparse matrix
a: Each non-zero element in the sparse matrix adopts a triple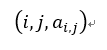
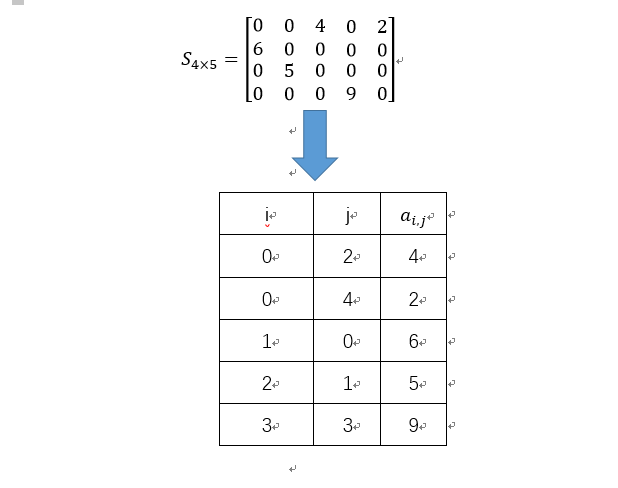
The only one is determined, so a triple linear table is finally formed, so its storage method is sequential storage structure. As shown in the figure:
b: code implementation
#include <stdio.h>
#include <malloc.h>
#include <string.h>
typedef int ElemType;
#define M 4
#define N 5
#define MaxSize 200
//Structure declaration
typedef struct
{
int r; //Line number
int c; //Column number
ElemType d;
}SpMatrix;
typedef struct
{
int rows; //Number of rows
int cols; //Number of columns
int nums; //Number of non-zero elements
SpMatrix data[MaxSize];
}TriPle; //Triple order table definition
//Create its triples
void CreatMat(TriPle &t,ElemType S[M][N])
{
int i,j;
t.rows=M;
t.cols=N;
t.nums=0;
for(i=0;i<M;i++)
{
for(j=0;j<N;j++)
if(S[i][j]!=0)
{
t.data[t.nums].r=i;
t.data[t.nums].c=j;
t.data[t.nums].d=S[i][j];
t.nums++;
}
}
}
//Triple element assignment
int Value(TriPle &t,ElemType x,int i,int j)
{
int k=0,k1;
if(i>=t.rows || j>=t.cols)
return 0;
while(k<t.nums && i>t.data[k].r) //Find row
k++;
while(k<t.nums && i==t.data[k].r && j>t.data[k].c) //Find column
k++;
if(k<t.nums && t.data[k].r==i && t.data[k].c==j) //Determine whether such elements exist
t.data[k].d=x;
else //Insert an element when such an element does not exist
{
for(k1=t.nums-1;k1>=k;k1--)
{
t.data[k1+1].r=t.data[k1].r;
t.data[k1+1].c=t.data[k1].c;
t.data[k1+1].d=t.data[k1].d;
}
t.data[k].r=i;
t.data[k].c=j;
t.data[k].d=x;
t.nums++;
}
return 1;
}
//Assigns the element value at the specified position to the variable
int Assign(TriPle t,ElemType &x,int i,int j)
{
int k=0;
if(i>=t.rows || j>=t.cols)
return 0;
while(k<t.nums && i>t.data[k].r) //Find row
k++;
while(k<t.nums && i==t.data[k].r && j>t.data[k].c) //Find column
k++;
if(k<t.nums && t.data[k].r==i && t.data[k].c==j)
x=t.data[k].d;
else
x=0; //No element representing zero was found in the triplet
return 1;
}
//Output triplet
void DispMat(TriPle t)
{
int i;
if(t.nums<=0)
return ;
printf("\t%d\t%d\t%d\n",t.rows,t.cols,t.nums);
printf("\t-----------------------------------\n");
for(i=0;i<t.nums;i++)
printf("\t%d\t%d\t%d\n",t.data[i].r,t.data[i].c,t.data[i].d);
}
void main()
{
TriPle t;
ElemType x;
ElemType S[M][N]={{0,0,4,0,2},{6,0,0,0,0},{0,5,0,0,0},{0,0,0,9,0}};
CreatMat(t,S);
printf("Triplet t express:\n");
DispMat(t);
printf("implement S[2][1]=6\n");
Value(t,6,2,1);
printf("Triplet t express:\n");
DispMat(t);
printf("seek x=S[2][1]\n");
Assign(t,x,2,1);
printf("x=%d\n",x);
}
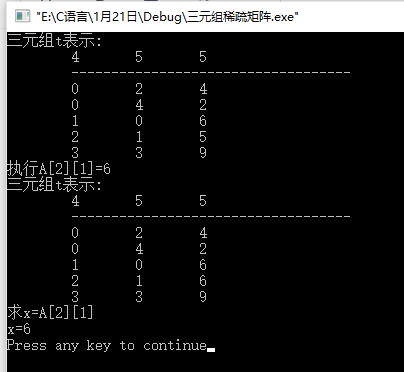
c: result demonstration
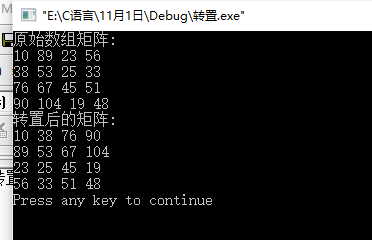
V. explanation of examples
Implement the device operation of an integer array S of m*n.
Code implementation:
#include <stdio.h>
int main()
{
int S[4][4]={{10,89,23,56},{38,53,25,33},{76,67,45,51},{90,104,19,48}};
int i,j,temp;
printf("Original array matrix:\n");
for(i=0;i<4;++i)
{
for(j=0;j<4;++j)
{
printf("%d ",S[i][j]);
}
printf("\n");
}
for(i=0;i<4;++i)
{
for(j=0;j<4;++j)
{
if(j>i)
{
temp=S[i][j];
S[i][j]=S[j][i];
S[j][i]=temp;
}
}
}
printf("Transposed matrix:\n");
for(i=0;i<4;++i)
{
for(j=0;j<4;++j)
{
printf("%d ",S[i][j]);
}
printf("\n");
}
return 0;
}Structure demonstration: