Maximum cumulative product of a subarray
Title: given a double type array arr, where the elements can be positive, negative and 0, return the maximum product of the cumulative multiplication of the subarray.
For example: arr = [-2.5, 4, 0, 3, 0.5, 8, - 1], cumulative multiplication of subarray [3, 0.5, 8] can obtain the maximum product 12, so 12 is returned.
Subarray problem routine
Find the maximum / minimum / optimal solution in the subarray under a certain standard / condition: under the standard, solve the answer of the subarray starting or ending with each i position, then the global answer must be in it.
analysis:
What is the maximum cumulative product of the subarray ending in each position i? If you find out each position, the answer must be in it.
What is the maximum cumulative product of subarrays that must end at position i, column possibilities:
1. The subarray ending with i is a subarray, which does not expand to the left, that is, it contains only i;
2. The subarray ending with i expands to the left;
- When arr[i] > 0, the maximum cumulative product is the maximum cumulative product * arr[i];
- When arr[i] < 0, the maximum cumulative product is the minimum cumulative product * arr[i];
So for each position, we need to get the maximum cumulative product and the minimum cumulative product ending at that position.
public class MaxMulitiple {
public static double maxMulitiple(double[] arr){
if(arr == null || arr.length == 0){
return 0;
}
double max = arr[0]; // Record the maximum cumulative product ending at position i
double min = arr[0]; // Record the minimum cumulative product ending at position i
double res = arr[0]; // Final results
// Record the cumulative product of the three cases ending at position i
double possible1 = 0;
double possible2 = 0;
double possible3 = 0;
// Starting from 1 as the end of the subarray, traverse each element as the end of the subarray in turn
for(int i = 1; i < arr.length; i++){
// Case 1: the i position itself is a subarray
possible1 = arr[i];
// Case 2: arr [i] > 0 I position as the end of the subarray, expanding the maximum cumulative product of i-1 position to the left
possible2 = max * arr[i];
// Case 3: arr [i] < 0 I position as the end of the subarray, expanding the minimum cumulative product of i-1 position to the left
possible3 = min * arr[i];
// Maximum and minimum in three cases
max = Math.max(Math.max(possible1,possible2), possible3);
min = Math.min(Math.min(possible1,possible2), possible3);
res = Math.max(max, res);
}
return res;
}
}Second, the shortest subarray length to be sorted
Title: given an unordered array arr, find the shortest subarray length to sort. For example, arr = [1, 5, 3, 4, 2, 6, 7] returns 4, because only [5, 3, 4, 2] needs sorting.
Requirements: time complexity O(N), additional space complexity O(1).
Assuming that the array is [a B C D E F G I J K L M n], if abc is ordered, mn is ordered, and defghijkl in the middle is disordered, we can know that if it is a normal ascending sequence, the left must be less than any value on the right, and the right must be greater than any value on the left.
Analysis: traverse from left to right and from right to left respectively to find out the failure positions on the left and right sides, and the array in the middle of the two failure positions is the shortest sub array to be sorted.
Steps:
1. Traverse from left to right to find the rightmost range of inappropriate numbers: traverse from left to right. If maxleft > the current element, record its position to invalidRight and traverse all the way to the rightmost [it can be seen that invalidRight is the last number that does not meet the sorting requirements, and its right is greater than invalidRight]
2. Traverse from right to left to find the leftmost range of inappropriate numbers: traverse from right to left. If the current element > minRight, record its position as invalidLeft, and traverse to the leftmost [it can be seen that invalidLeft , is the last number that does not meet the sorting requirements, and its left is fully less than minRight]
3. invalidRight - invalidLeft + 1 is the shortest subarray length to sort.
public class GetMinLengthForSort {
public static int getMinLengthForSort(int[] arr){
if(arr == null || arr.length < 2){
return 0; // No sorting is required
}
int maxLeft = arr[0]; // Left largest
int minRight = arr[arr.length - 1]; // Right smallest
// These two pointers record the invalid positions on the left and right sides respectively
int invalidLeft = 0;
int invalidRight = -1; // When the array is originally ordered: invalidRight - invalidLeft + 1 = 0
// 1. Traversal from left to right: find the rightmost range of inappropriate numbers
// If the traversed maximum value is greater than the current value, the current value must be invalid. When sorting, the maximum value is in the current position or a more right position
for(int i = 1; i < arr.length; i++){
if(maxLeft > arr[i]){
// If the maximum value that has been traversed is greater than the current value, the rightmost invalid position is recorded
invalidRight = i;
}else{
// If the traversed maximum value is less than or equal to the current value, the traversed maximum value is updated to the current value
maxLeft = arr[i];
}
}
// 2. Traversal from right to left: find the leftmost range of inappropriate numbers
// If the traversed minimum value is less than the current value, the current value is invalid. When sorting, the minimum value is in the current position or a more left position
for(int i = arr.length - 2; i >= 0; i--){
if(minRight < arr[i]){
// If the minimum value that has been traversed is less than the current value, the leftmost invalid position is recorded
invalidLeft = i;
}else{
// Update minimum
minRight = arr[i];
}
}
// invalidRight is the rightmost range of inappropriate numbers, and invalidLeft is the leftmost range of inappropriate numbers
// invalidRight - invalidLeft + 1 is the number of unfit numbers
return invalidRight - invalidLeft + 1;
}
public static void main(String[] args) {
int[] arr = {1,2,3,4,5,6};
System.out.println(getMinLengthForSort(arr));
}
}Length of the three longest integrable subarrays
Title: the length of the longest integrable subarray. Given an integer array arr, return the length of the largest integrable subarray. For example, the maximum integrable subarray of [5,5,3,2,6,4,3] is [5,3,2,6,4], so 5 is returned.
Firstly, the definition of integrable array is given: if the absolute value of each adjacent number difference is 1 after sorting, the array is an integrable array. For example, [5,3,4,6,2] is sorted as [2,3,4,5,6], and the absolute value conforming to the difference between each two adjacent numbers is 1, so this array is an integrable array.
analysis:
1. Violence:
List all subarrays [N^2], then copy each subarray, sort it (NlogN), and traverse it. If it is not satisfied, there are O(N^3logN) [subarray: one or more consecutive integers in the array form a subarray];
2. Optimization:
Later, when you see complex standards, first change them to concise standards. New standard: if an array is integrable:
1) No duplicate value;
2) If the maximum minus the minimum is equal to the number of arrays minus 1, it is integrable.
The complexity of all subarrays is O(N^2), and the complexity of judging whether each subarray is integrable is O(1) (you can judge whether the array is integrable only by recording min and max during traversal).
public class LongestIntegrationLength {
public static int getLongest(int[] arr){
if(arr == null || arr.length == 0){
return 0;
}
int maxLen = 0;
HashSet<Integer> set = new HashSet<>();
// Try a subarray that starts with each i
for(int i = 0; i < arr.length; i++){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int j = i; j < arr.length; j++){
if(set.contains(arr[j])){
// If it contains duplicate numbers, the next digit is directly used as the beginning of the array
break;
}
set.add(arr[j]);
max = Math.max(max, arr[j]);
min = Math.min(min, arr[j]);
// The number of arrays is: j - i + 1, and then minus 1, that is: j - i
if(max - min == j - i){
// The maximum minus minimum is equal to the length of the current array, indicating that the span between each number is 1 and can be integrated
maxLen = Math.max(maxLen, j - i + 1);
}
}
// Each time you start a subarray with a new number, clear the set first
set.clear();
}
return maxLen;
}
public static void main(String[] args) {
int[] arr = { 5, 5, 3, 2, 6, 4, 3 }; // 5, 3, 2, 6, 4
System.out.println(getLongest(arr)); // 5
}
}Four shortest unordered continuous subarrays
Title: given an integer array, you need to find a continuous subarray. If you sort the subarray in ascending order, the whole array will be sorted in ascending order. The subarray you found should be the shortest. Please output its length.
Example 1:
Input: [2, 6, 4, 8, 10, 9, 15]
Output: 5
Explanation: you only need to sort [6, 4, 8, 10, 9] in ascending order, and the whole table will be sorted in ascending order.
explain:
The input array length range is [1, 10000].
The input array may contain duplicate elements, so ascending means
Double pointer idea
1. The array temp is copied from nums, and then the temp is sorted from small to large;
2. Then use the double pointer, one from the head, one from the tail, close to the middle; If equal, + + or --; If the values pointed to by the left and right pointers are not equal, break;
3. The size to be sorted is [left, right], and the size is: right - left + 1.
public class FindUnsortedSubarray_581 {
public static int findUnsortedSubarray(int[] nums) {
if(nums == null || nums.length < 1){
return -1;
}
int[] temp = nums.clone();
// Sort the temp array from small to large
Arrays.sort(temp);
// Double pointer: one pointing to the head and one pointing to the tail
int left = 0;
int right = nums.length - 1;
while(left < right){
boolean flag = true;
// After finding the unequal position, the corresponding pointer stops. When the other pointer stops without meeting the conditions, it break s
if(nums[left] == temp[left]){
left++;
flag = false;
}
if(nums[right] == temp[right]){
right--;
flag = false;
}
// flag is true only when the positions pointed to by the two pointers are not equal, then break
if(flag == true){
break;
}
}
return left >= right ? 0 : right - left + 1;
}
public static void main(String[] args) {
int[] arr = {1, 3, 2, 2, 2};
System.out.println(findUnsortedSubarray(arr)); // 4
}
}Maximum sum of five consecutive subarrays
Title: enter an integer array. There are both positive and negative numbers in the array. One or more consecutive integers in the array form a sub array. Find the maximum value of the sum of all subarrays. The required time complexity is O(n).
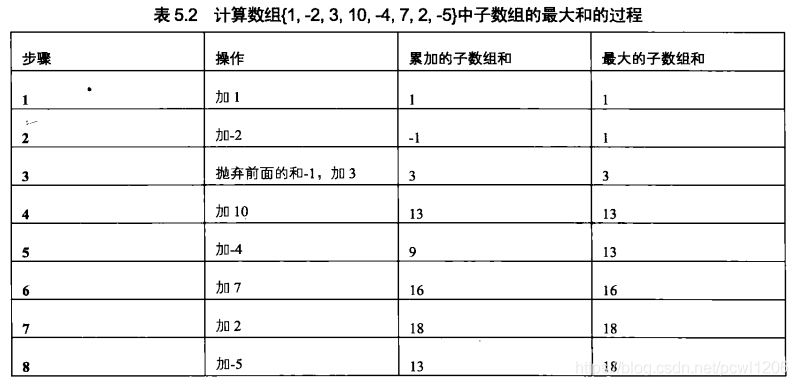
For example, the input array is {1, - 2, 3, 10, - 4, 7, 2, - 5}, and the largest subarray is {3, 10, - 4, 7, 2}, so the sum of the output subarray is 18.
Seeing this topic, many people can think of the most intuitive method, that is, list all sub arrays of the array and find their sum. An array of length N, with a total of n(n+1)/2 sub arrays. Calculating the sum of all subarrays also takes O() as soon as possible. Usually the most intuitive method is not the best method, and the interviewer will remind us that there are faster methods.
1. An example is given to analyze the law of array
We try to accumulate each number in the sample array from beginning to end. Initialization and are 0 The first step is to add the first number, and the sum is 1 Next, in the second step, add the number - 2, and becomes - 1 Step 3 add the number 3 We note that since the previously accumulated sum is - 1, less than 0, if you add - 1 and 3, the sum is 2, which is smaller than 3 itself. That is, the sum of subarrays starting from the first number will be less than the sum of subarrays starting from the third number. So we don't have to consider from the first subarray, and the previously accumulated sum is also discarded.
We start accumulating again from the third number, and the sum is 3 Next, add 10 in the fourth step to get the sum of 13 In step 5, add - 4 and the sum is 9 We find that - 4 is a negative number, so the sum of - 4 is smaller than the original. So we have to save the sum of and 13, which may be the sum of the largest subarray. In step 6, add the numbers 7, 9 and 7, and the result is 16. At this time, the sum is larger than the previous maximum sum of 13. Update the sum of the largest sub array from 13 to 16 In step 7, add 2, and the sum is 18. At the same time, we also need to update the sum of the largest sub array. In step 8, add the last number - 5. Since the result is 13, which is less than the previous maximum sum of 18, the sum of the final maximum sub array is 18, and the corresponding sub array is {3, 10, - 4, 7, 2}.
package com.zju.offer.arrays;
/**
* Maximum sum of consecutive subarrays
*/
public class FindMaxSumOfSubArray {
public int findMaxSumOfSubArray(int[] array){
if(array.length == 0){
return 0;
}
int greatest = 0x80000000;
int curSum = 0;
for (int i = 0; i < array.length; i++) {
if(curSum <= 0){
// If curSum is negative, update surSum to array[i]
curSum = array[i];
}else{
// If curSum is a positive number, the array[i] is accumulated to curSum
curSum += array[i];
}
if(curSum > greatest){
// Update maximum
greatest = curSum;
}
}
return greatest;
}
// test
public static void main(String[] args) {
FindMaxSumOfSubArray find = new FindMaxSumOfSubArray();
int[] array = {-1,-2,-3,-10,-4,-7,2,-5};
int maxSumOfSubArray = find.findMaxSumOfSubArray(array);
System.out.println(maxSumOfSubArray);
}
}Solution 2: using dynamic programming method
We can also apply the idea of dynamic programming to analyze this problem. If the function f(i) is used to represent the maximum sum of subarrays ending with the ith number, we need to find max[f(i)], where 0
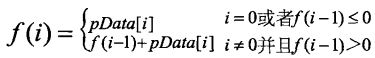

The following is an answer analysis from niuke.com:
F(i): the maximum value of the sum of the array of sub elements with array[i] as the end element, and the relative position of the elements of the sub array remains unchanged;
- F(i) = max(F(i - 1) + array[i], array[i])
res: the maximum value of the sum of all subarrays
- res = max(res, F(i))
package com.zju.offer.arrays;
/**
* Maximum sum of consecutive subarrays
*/
public class FindMaxSumOfSubArray {
// Using dynamic programming method
public int findGreatestSunOfSubArray(int[] array){
if(array.length == 0){
return 0;
}
// Records the maximum value in the current subarray
int res = array[0];
// The maximum value of a contiguous array containing array[i]
int max = array[0];
for (int i = 1; i < array.length; i++) {
max = Math.max(max + array[i], array[i]);
res = Math.max(max, res);
}
return res;
}
// test
public static void main(String[] args) {
FindMaxSumOfSubArray find = new FindMaxSumOfSubArray();
int[] array = {-1,-2,-3,-10,-4,-7,2,-5};
int maxSumOfSubArray = find.findGreatestSunOfSubArray(array);
System.out.println(maxSumOfSubArray);
}
}