Balanced search binary tree is a kind of highly balanced binary sorting tree, what is called highly balanced? It means that either it is an empty tree, or its left and right subtrees are balanced binary trees. Because there is no absolute balance in the binary tree, the absolute value of the difference between the depth of the left subtree and the right subtree is required to be no more than 1. We also call the value of the depth of the left subtree of the node on the binary tree minus the depth of the right subtree the balance factor

Properties of AVL tree:
(1) The absolute value of the difference between the height of left and right subtrees shall not exceed 1
(2) Each left and right subtree in the tree is an AVL tree
(3) Each node has an equilibrium factor (the equilibrium factor of any node is - 1,0,1)

insert
The insertion operation is similar to the previous binary search tree insertion, except that AVL focuses on updating the balance factor through rotation operation according to the situation after insertion.

bool Insert(const K& key, const V& value)
{
    if (_root == NULL)//Root insertion node is empty direct
    {
        _root = new Node(key, value);
        return true;
    }
    Node* parent = NULL;
    Node* cur = _root;
    //Find the location of the parent node to insert
    while (cur)
    {
        if (key < cur->_key)
        {
            parent = cur;
            cur = cur->_left;
        }
        else if (key > cur->_key)
        {
            parent = cur;
            cur = cur->_right;
        }
        else
            return false;
    }
    cur = new Node(key, value);
    //Determine whether to insert it on the left or right of the parent node
    if (key < parent->_key)
    {
        parent->_left = cur;
        cur->_parent = parent;
    }
    else
    {
        parent->_right = cur;
        cur->_parent = parent;
    }
    //Update balance factor
    while (parent)
    {
        if (cur == parent->_left)
        {
            parent->_bf -= 1;//Insert balance factor to the left minus one
        }
        else
        {
            parent->_bf += 1;//Insert balance factor plus one on the right
        }
        //|bf|=0 the height of the tree does not change, and it will not be updated upward
        if (parent->_bf == 0)
        {
            return true;
        }
        //|bf|=1 tree height has changed, continue to update
        else if (parent->_bf == -1
            || parent->_bf == 1)
        {
            cur = parent;
            parent = cur->_parent;
        }
        //|bf|=2 no longer updated, rotate and balance
        else if (parent->_bf == -2
            || parent->_bf == 2)
        {
            if (parent->_bf == 2)
            {
                if (cur->_bf == 1)
                    RotateL(parent);
                else
                    RotateRL(parent);
            }
            else
            {
                if (cur->_bf == -1)
                    RotateR(parent);
                else
                    RotateLR(parent);
            }
        }
        else
        {
            assert(false);
        }
    }
    return true;
}

Left spin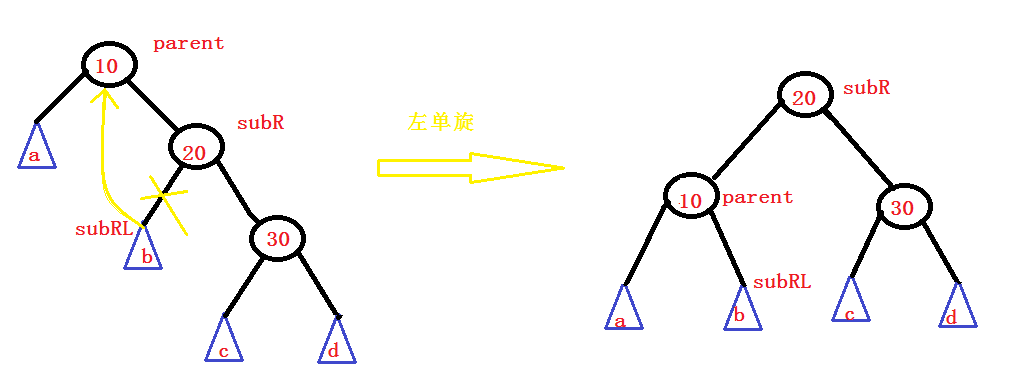

void RotateL(Node* parent)
{

    Node* SubR = parent->_right;
    Node* SubRL = SubR->_left;

    parent->_right = SubRL;
    if (SubRL != NULL)
    {
        SubRL->_parent = parent;
    }
    Node* tmp = parent->_parent;//Create ancestor node
    SubR->_left = parent;
    parent->_parent = SubR; 
    if (tmp == NULL)
    {
        _root = SubR;
        SubR->_parent = NULL;
    }
    else if (tmp->_left == parent)
    {
        tmp->_left = SubR;
    }
    else
    {
        tmp->_right = SubR;
    }   
    SubR->_parent = tmp;
    SubR->_bf = parent->_bf = 0;//Update balance factor
}

Right single rotation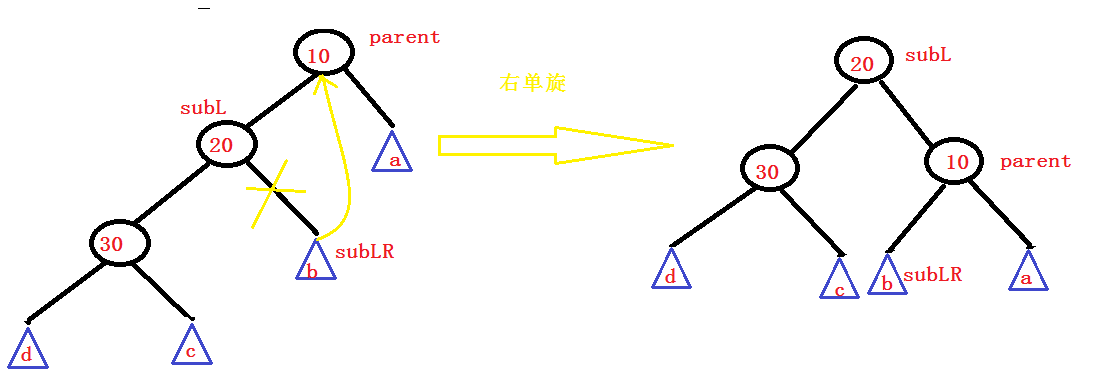

    void RotateR(Node* parent)
    {
        Node* SubL = parent->_left;
        Node* SubLR = SubL->_right;

        parent->_left = SubLR;
        if (SubLR != NULL)
        {
            SubLR->_parent = parent;
        }
        Node* tmp = parent->_parent;
        SubL->_right = parent;
        parent->_parent = SubL;
        if (tmp == NULL)
        {
            _root = SubL;
        }
        else if (tmp->_left == parent)
        {
            tmp->_left = SubL;
        }
        else
        {
            tmp->_right = SubL;
        }
        SubL->_parent = parent;
        parent->_bf = SubL->_bf = 0;
    }

Left and right rotation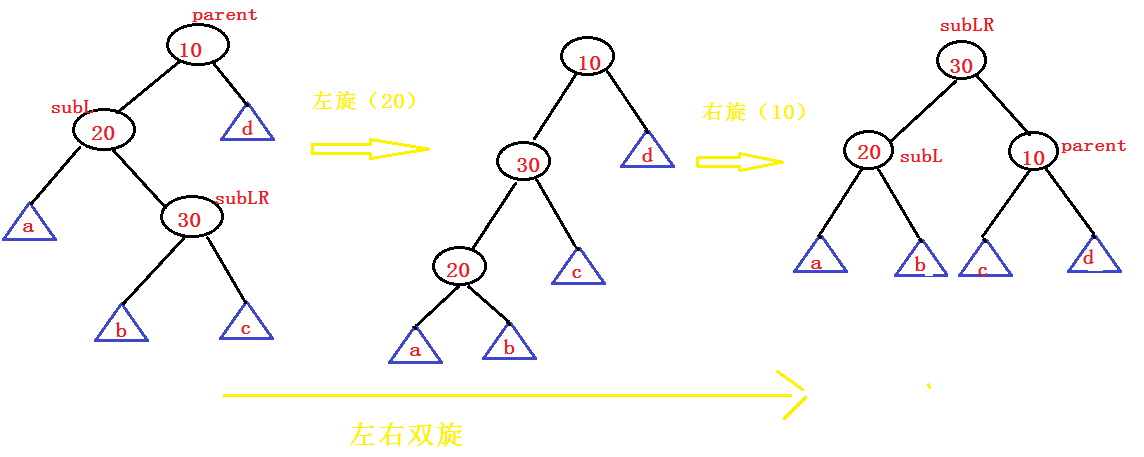

(1) Scenario 1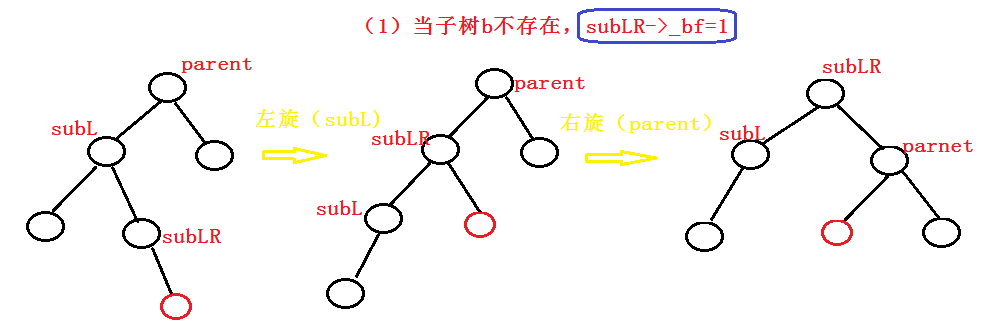

(2) Scenario 2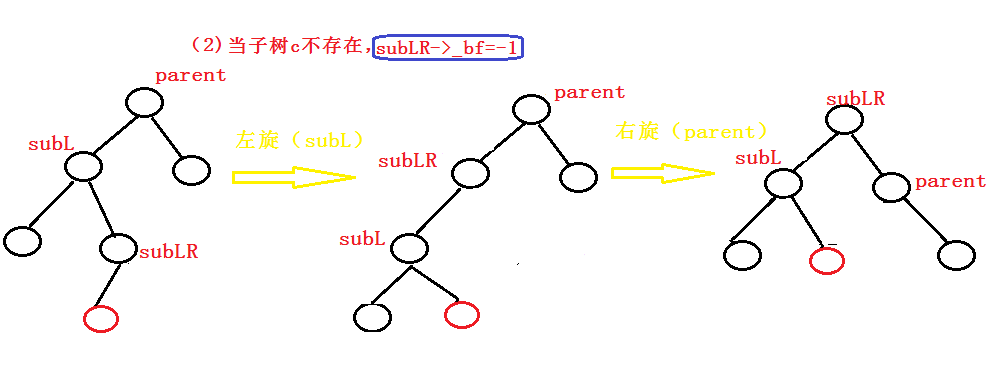

(3) Scenario 3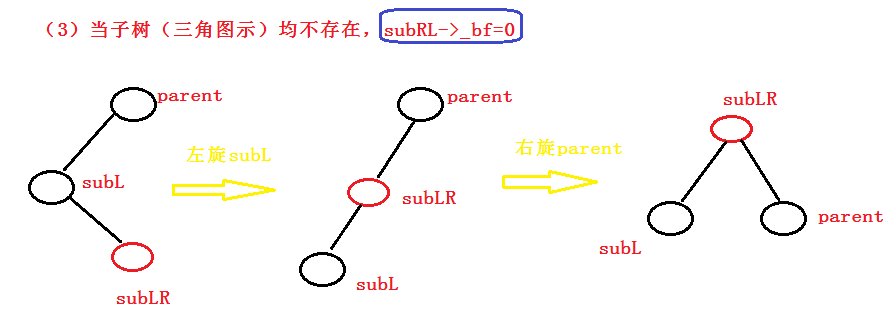

void RotateLR(Node* parent)
{
    Node* SubL = parent->_left;
    Node* SubLR = SubL->_right;
    int bf = SubLR->_bf;

    RotateL(SubLR);
    RotateR(parent);

    if (bf == 1)//Scene (1)
    {
        parent->_bf = SubLR->_bf = 0;
        SubL->_bf = -1;
    }
    else if (bf == -1)//Scenario (2)
    {
        parent->_bf = 1;
        SubLR->_bf = SubL->_bf = 0;
    }
    else if (bf == 0)//Scenario (3)
        parent->_bf = SubL->_bf = SubLR->_bf = 0;
    else
        assert(false);
}

The right left double rotation is similar to the left and right double rotation, which is not analyzed in detail here.