
catalog:
I Concept & principle
Previously, we understood the binary search tree, but we found that if the data is orderly or close to orderly, the binary search tree will degenerate into a single tree
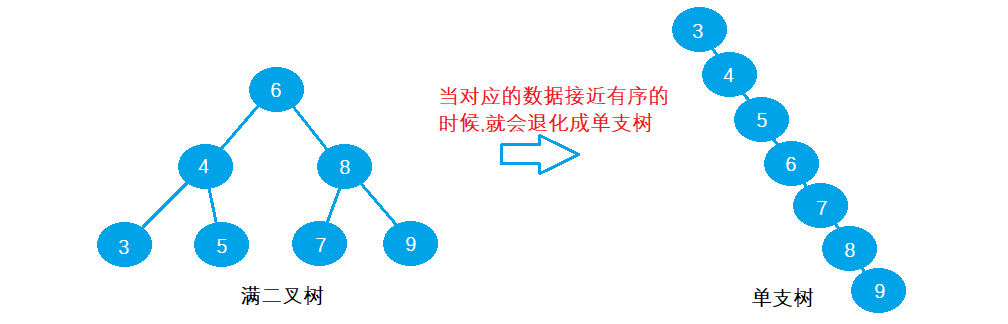
AVL tree is a balanced binary tree. It just adds a balance factor to the binary search tree to form the current balanced binary tree Binary search tree link
^
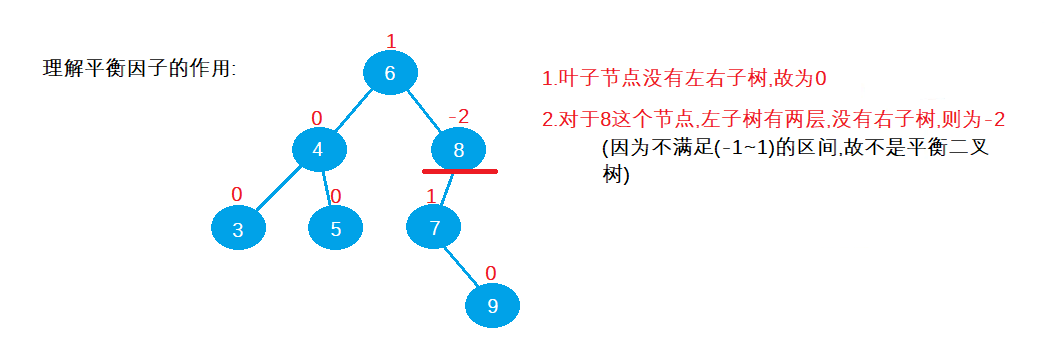
Here we focus on understanding the balance factor
II Balance factor
Balance factor: the balance factor is an integer value to judge whether the corresponding binary tree is balanced, so as to stabilize the binary tree and prevent the binary tree from degenerating into the above single branch tree
Rules:
1. There is a balance factor on each corresponding node to indicate whether the binary tree is balanced
~
2. Balance factor of each node = layers of right subtree - layers of left subtree
~
3. When the corresponding balance factor is (- 1 ~ 1), it is a balanced binary tree, otherwise it needs to be adjusted
III definition
There is a left child node inside the AVL tree Right child node Parent node Corresponding stored data There is also the balance factor. We create a structure and encapsulate it as something that should be stored inside a node
template<class T> //Generic declaration
struct AVLNode{ //Created structure
AVLNode<T>* _parent; //Create corresponding parent node
AVLNode<T>* _left; //Left child
AVLNode<T>* _right; //Right child
T _val; //Internal corresponding value
//Balance factor
int _bf;
AVLNode(const T& val = T()) //Initialize a corresponding node
:_parent(nullptr)
, _left(nullptr)
, _right(nullptr) //Node assigned nullptr
, _val(val) //Direct data transfer
, _bf(0) //The equilibrium factor is directly reduced to 0
{}
};
In this way, all the things needed to create a corresponding node are passed in, When using this structure later, we only need to give it an alias, and then create it in the way of new
IV Rotation of AVL tree
1. Left hand interface understanding
Understanding of the left rotation interface: because the balance factor of the node will change after the AVL tree is inserted, for this reason, we need to operate the left rotation of the binary tree inserting a new node, so as to restore the binary tree to the balanced binary tree
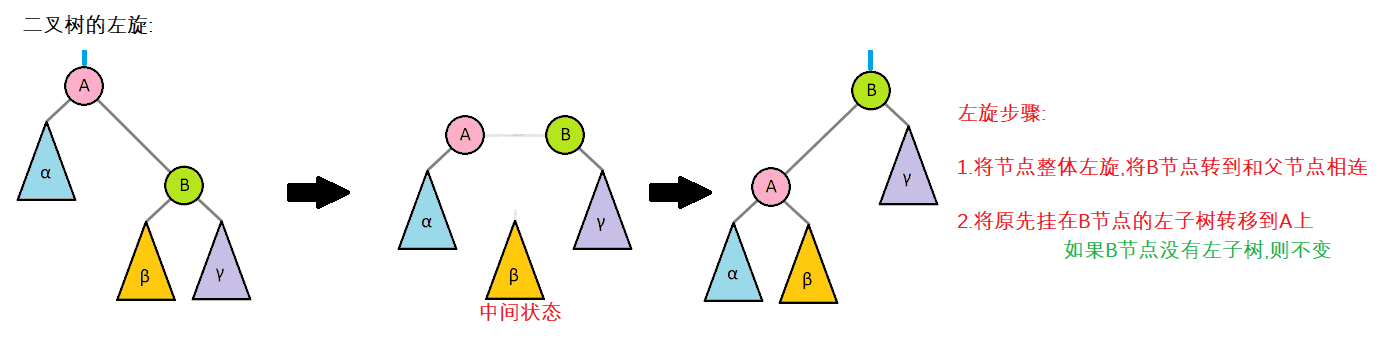
void RotateL(Node* parent){
Node* subR = parent->_right; //What is defined here is the right subtree corresponding to the parent node, that is, B
Node* subRL = subR->_left; //Here we get the left subtree of node B, that is, the node to be converted by left rotation
subR->_left = parent; //Connect B to the corresponding parent node
parent->_right = subRL; //Connect the right subtree of the parent node with B
if (subRL) //When the node in this intermediate state exists
subRL->_parent = parent; //Then let the parent node of its child node point to the real parent node
if (parent == _root){ //When the parent node is the root node
_root = subR; //Point to parent node
subR->_parent = nullptr; //Its internal pointer is converted to null
}
else{ //If both exist
Node* pparent = parent->_parent; //Defines the parent node of the parent
if (pparent->_left == parent) //If the parent node is to the left of the grandfather node, point it to
pparent->_left = subR;
else
pparent->_right = subR; //Otherwise, it is the right direction
subR->_parent = pparent; //Finally, let the parent node generated by its left rotation point to the grandfather's node
}
parent->_parent = subR; //Point the parent node of the parent to the child node of the rotation
parent->_bf = subR->_bf = 0; //Because after left rotation, the internal balance factor becomes 0
}
The explanation of sinistral rotation has been relatively clear. The main thing is to draw pictures to understand the process step by step
2. Right hand interface understanding
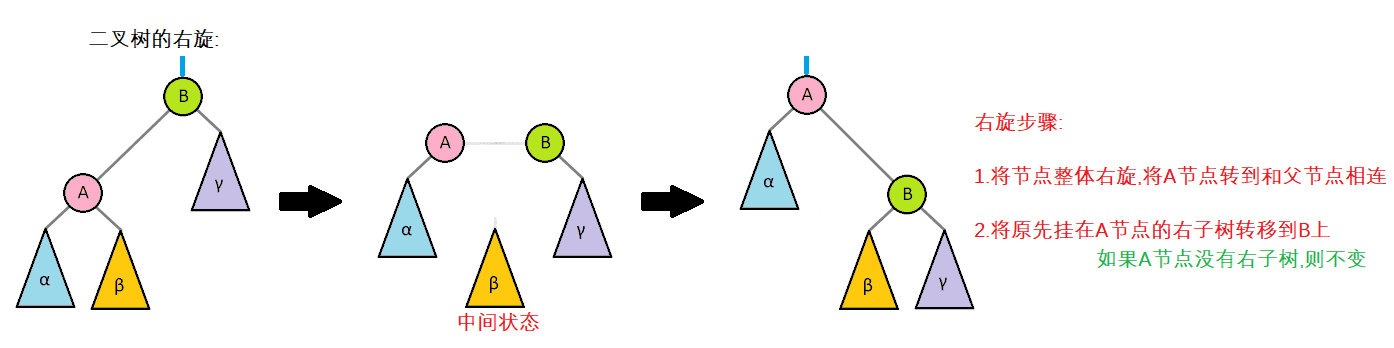
The right-handed operation is similar to the left-handed operation. We can understand it by analogy. I won't comment more
void RotateR(Node* parent){
Node* subL = parent->_left; //Similarly, create its corresponding node point
Node* subLR = subL->_right; //Its internal nodes point to
subL->_right = parent;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
//Determine whether the parent is the root node
if (parent == _root){
//Root node
_root = subL;
subL->_parent = nullptr;
}
else{
Node* pparent = parent->_parent;
if (pparent->_left == parent)
pparent->_left = subL;
else
pparent->_right = subL;
subL->_parent = pparent;
}
parent->_parent = subL;
subL->_bf = parent->_bf = 0;
}
3. Understanding of insert interface
The code about Insert here is connected. I just split it for easier understanding
For the implementation of inserting an element, we also first traverse the binary tree, find the corresponding addition position, and insert the corresponding data. We also need to use left-hand and right-hand operations to realize the balanced binary tree according to the insertion position
bool insert(const T& val){ //Insert function
//Binary search tree
if (_root == nullptr){
_root = new Node(val); //If the root node is empty, it is directly created as the root node
return true;
}
Node* cur = _root; //Otherwise, the corresponding root node is created
Node* parent = nullptr; //Parent node is null
while (cur){ //There is a corresponding insertion position
parent = cur; //Insert data
if (cur->_val == val)
return false;
else if (cur->_val > val)
cur = cur->_left;
else
cur = cur->_right;
}
cur = new Node(val); //Create a new Node with Node
if (parent->_val > val)
parent->_left = cur;
else
parent->_right = cur;
cur->_parent = parent;
//Adjustment, starting from parent
while (parent){
//Update the balance factor of the parent
if (parent->_left == cur)
--parent->_bf;
else
++parent->_bf;
if (parent->_bf == 0) //parent short subtree height + 1
break;
else if (parent->_bf == 1 || parent->_bf == -1){
//Continue to update upward
cur = parent;
parent = parent->_parent;
}
else if (abs(parent->_bf) == 2){
The above is the understanding of inserting nodes, and the following is the adjustment of the binary tree after inserting elements
(1) The new node is inserted to the left of the higher left subtree - left left: right single rotation
The distinction here is achieved by the size of the balance factor between the parent node and its corresponding child node!!!
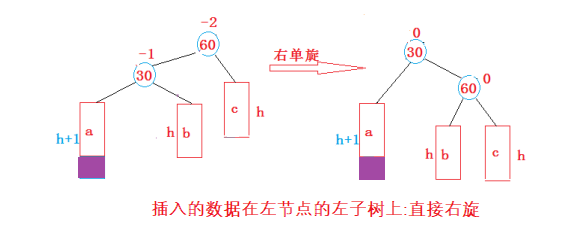
if (parent->_bf == -2 && cur->_bf == -1){
//If the left is high, it rotates right
RotateR(parent);
}
(2) The new node is inserted to the right of the higher right subtree - right right right: left single rotation
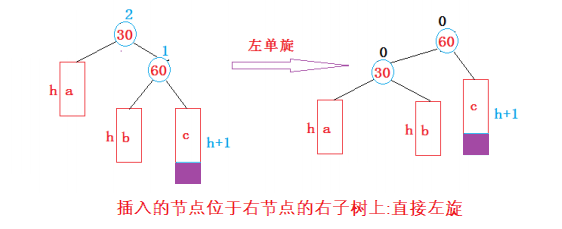
else if (parent->_bf == 2 && cur->_bf == 1){
RotateL(parent); //Parent node left rotation
}
(3) The new node is inserted to the right of the higher left subtree - left and right: first left single rotation and then right single rotation
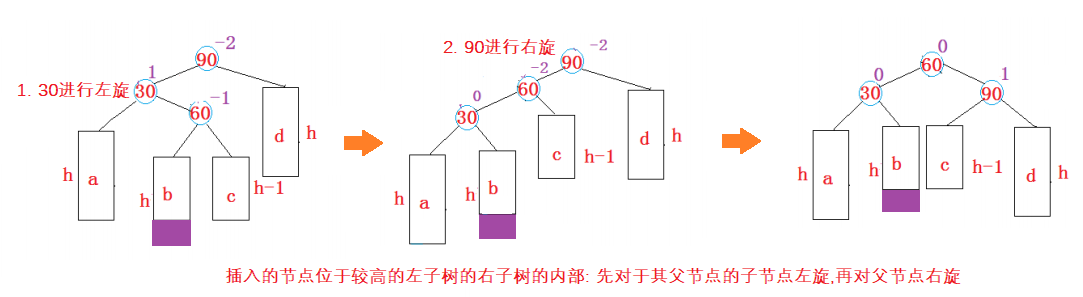
else if (parent->_bf == -2 && cur->_bf == 1){
Node* subLR = cur->_right;
int bf = subLR->_bf;
RotateL(cur); //First child node left rotation
RotateR(parent); //Rotate the parent node to the right
if (bf == 1){ Because when an update occurs,There will be a node update error,So update manually
parent->_bf = 0;
cur->_bf = -1;
}
else if (bf == -1){
parent->_bf = 1;
cur->_bf = 0;
}
}
(4) The new node is inserted to the left of the higher right subtree - right left: right single rotation first and then left single rotation
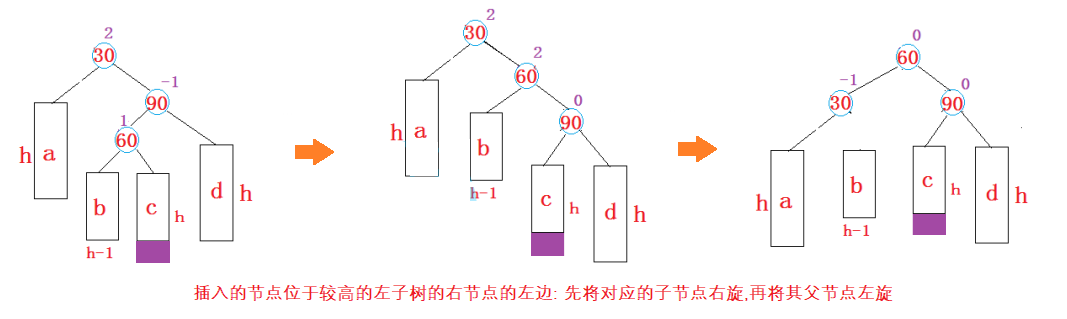
else if (parent->_bf == 2 && cur->_bf == -1){
//First obtain the bf corresponding to the subRL
Node* subRL = cur->_left;
int bf = subRL->_bf;
RotateR(cur);
RotateL(parent);
//After the occurrence of right left double rotation, the bf value of the corresponding child nodes may be different and need to be updated
//Here, the judgment method is used to distinguish the location of the linked node, and then update the corresponding bf
if (bf == 1){
cur->_bf = 0; Because when an update occurs,There will be a node update error,So update manually
parent->_bf = -1;
}
else if (bf == -1){
cur->_bf = 1;
parent->_bf = 0;
}
}
break;
}
}
return true;
}
V Print interface
The printing interface here is relatively simple. It mainly uses recursive method to cycle to the internal val
void inorder(){
_inorder(_root); //Call the following function
cout << endl;
}
void _inorder(Node* root){
if (root){
_inorder(root->_left); //First traverse the left node
cout << root->_val << " ";
_inorder(root->_right); //Traversing the corresponding right node
}
}
Vi Verify AVL tree interface
The verification of AVL tree is to judge whether it is a balanced binary tree by the balance factor and the height difference between the left and right subtrees
int Height(Node* root){ //Encapsulate the function to realize the height judgment of the corresponding child node
if (root == nullptr)
return 0;
int left = Height(root->_left);
int right = Height(root->_right);
return left > right ? left + 1 : right + 1;
}
bool _isBalance(Node* root){ //Function to judge whether it is balanced
if (root == nullptr)
return true;
//Check whether the balance factor is consistent with the height difference between the left and right subtrees
//Call the function to view the height of the corresponding subtree
int left = Height(root->_left);
int right = Height(root->_right);
if (right - left != root->_bf){
cout << " Node: " << root->_val << " bf:"
<< root->_bf << " height gap: " << right - 1; //output
return false;
}
return abs(root->_bf) < 2
&& _isBalance(root->_left) //Circular judgment
&& _isBalance(root->_right);
//Balanced output 1
}
bool isBalance(){ //The final encapsulated interface
return _isBalance(_root);
}
In general, we still understand the implementation of balanced binary tree insertion, because traversal and left-handed and right-handed operations will be involved during insertion, which is difficult to understand. We pay attention to the understanding of left-handed and right-handed, as well as left-handed and right-handed