AVL tree introduction and detailed explanation of each operation

Introduction to AVL tree
Implementation of AVL tree operation set
- rotate
  - RR insertion (left single rotation)
  - LL insertion (right single rotation)
  - RL insertion (right left double rotation)
  - LR insertion (left and right double rotation)
- insert
- delete
- ergodic
Complete code
- Code experiment

AVL tree introduction

AVL (Adelson velskii and Landis) tree is a binary search tree with equilibrium conditions. This condition is that the height difference between the left subtree and the right subtree of each node is at most 1 (the height of the empty tree is defined as - 1), and its depth is O(log N).
In short, an AVL tree is a binary lookup tree whose height difference between the left subtree and the right subtree of each node is at most 1.

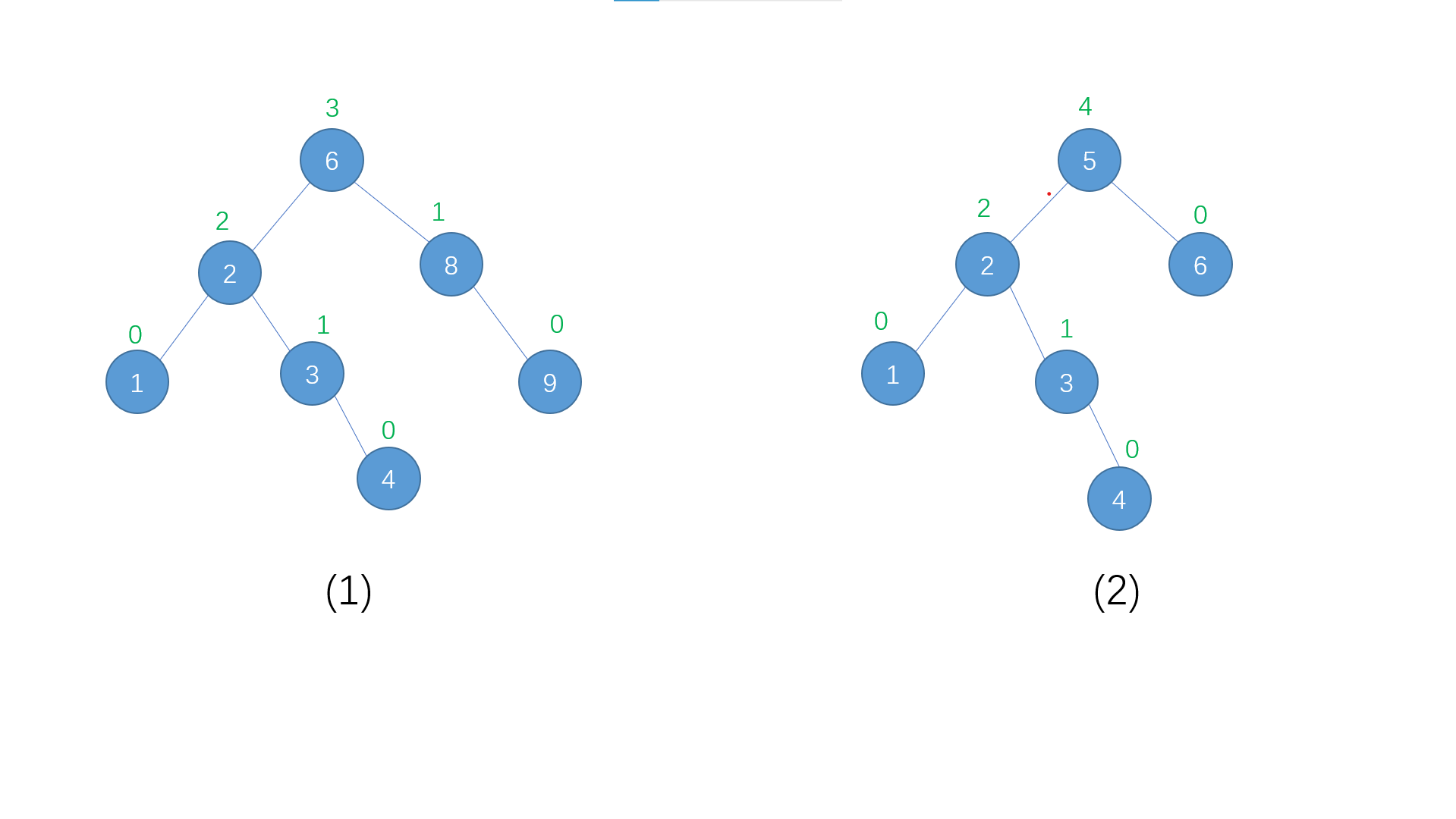
As shown in the figure above, the AVL tree on the left is not the AVL tree on the right, because the height difference between the left and right subtrees of node 5 in tree (2) exceeds 1.

The structure of AVL tree is as follows:

#include<stdio.h>
#include<stdlib.h>
#define Maxsize 20

typedef struct AVLTREE
{
	int Data;//Store data 
	int Height;//height 
	struct AVLTREE *Leftchild;//Left subtree 
	struct AVLTREE *Rightchild;//Right subtree 
}*AVLTree;

The height of the node is equal to the larger height of the left and right children of the node plus one.

Code for obtaining node height:

//Get node height 
int GetHeight(AVLTree root)
{
   if(root==NULL)
	return -1;
   else
    return MaxHeight(GetHeight(root->Leftchild),GetHeight(root->Rightchild))+1;
}

rotate

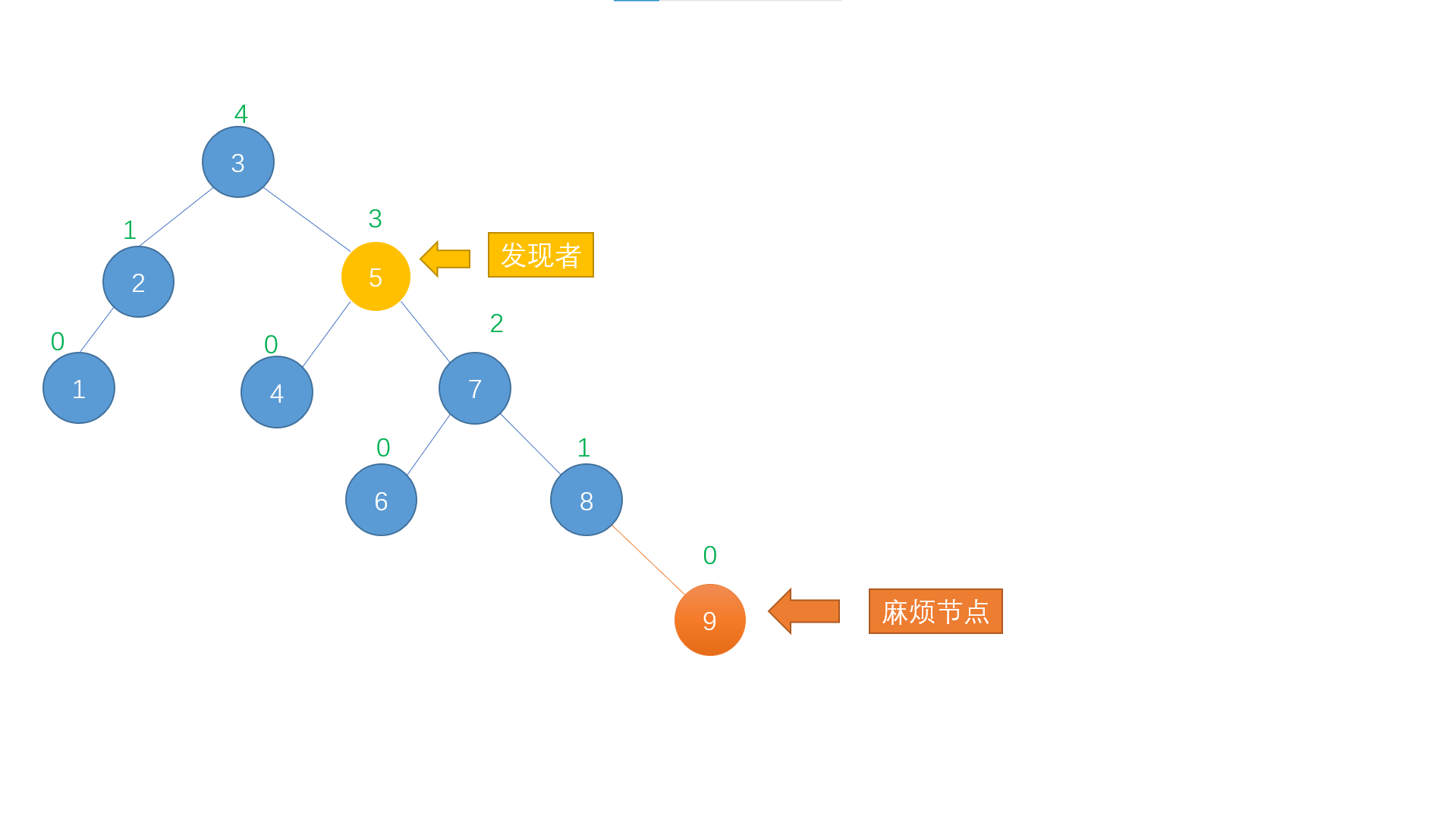
In the process of constantly adding new nodes to the AVL tree, it often leads to the "imbalance" of the AVL tree (that is, the height difference between the left and right subtrees of some nodes exceeds 1),

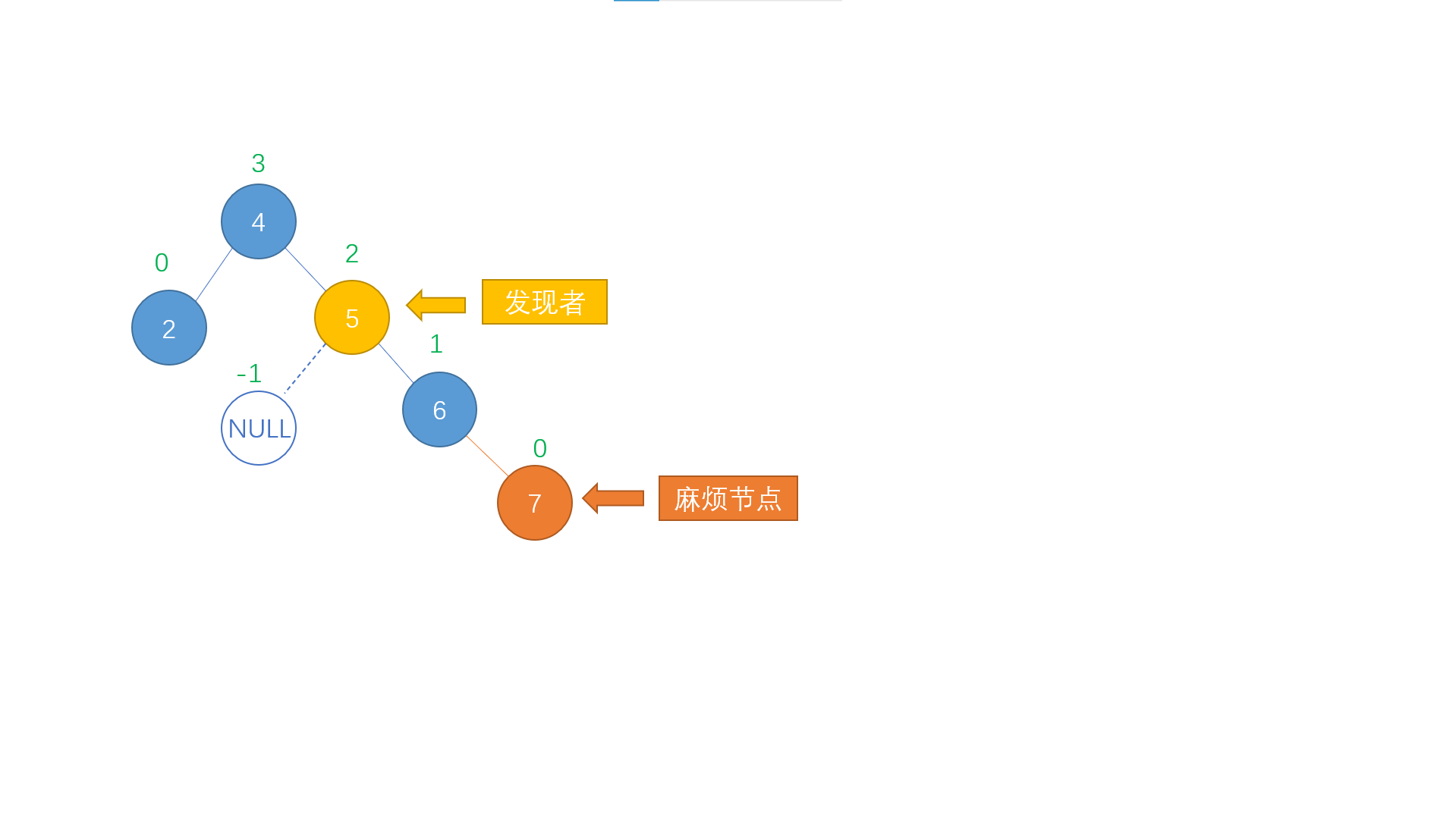
As shown in the figure above, the newly inserted node 7 leads to the imbalance of the tree. Although node 4 and node 5 are unbalanced at the same time, we only need to study and deal with the unbalanced node 5 closest to the new node. Here, we call the newly inserted node 7 causing the imbalance of the tree "trouble node" and the unbalanced node 5 closest to the trouble node "discoverer", Next, we will discuss the four forms of "discoverer" and "trouble node" in the insertion process.

RR insertion (left single rotation)

Take the example above as an example. It is a case of RR insertion

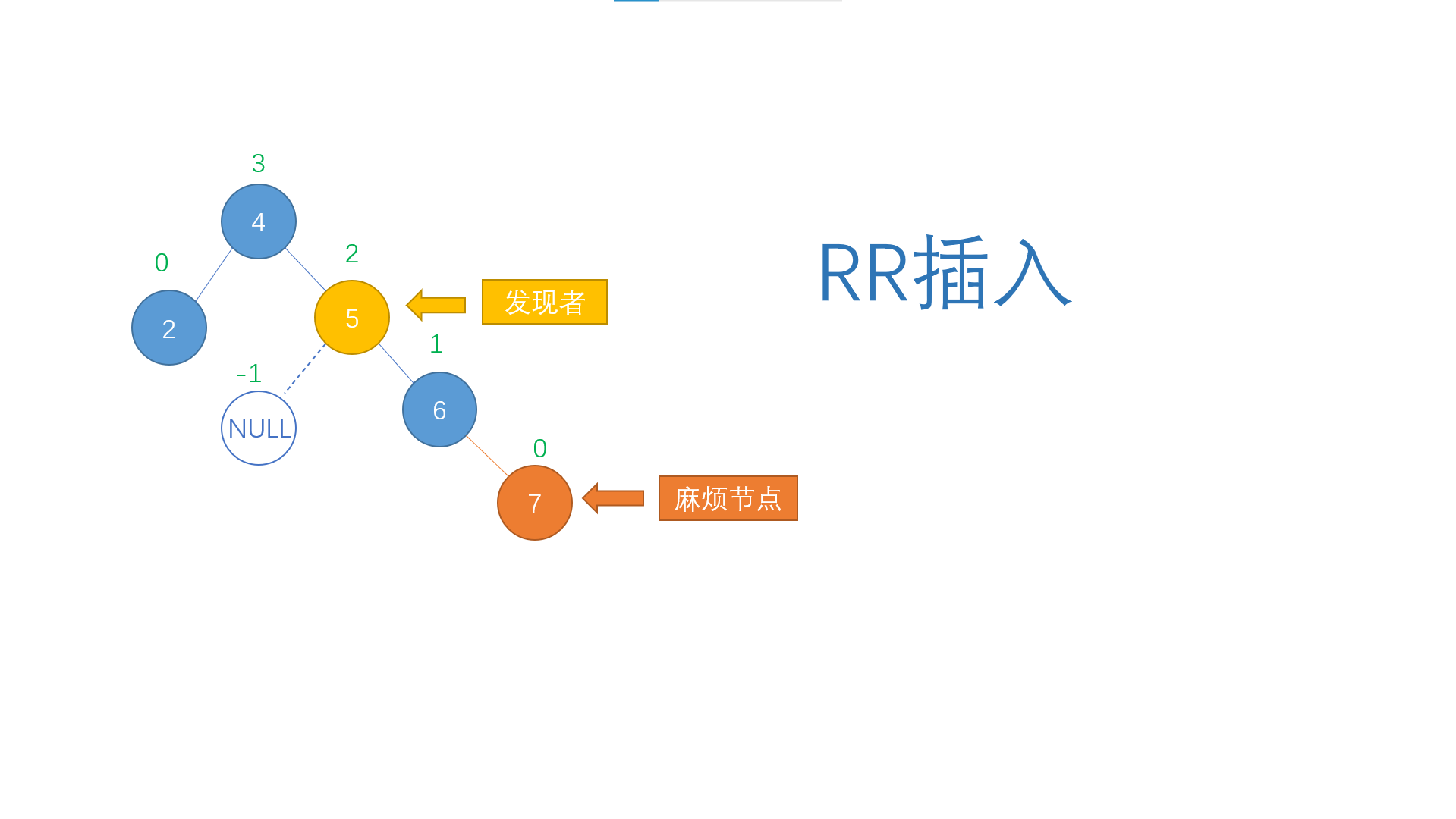
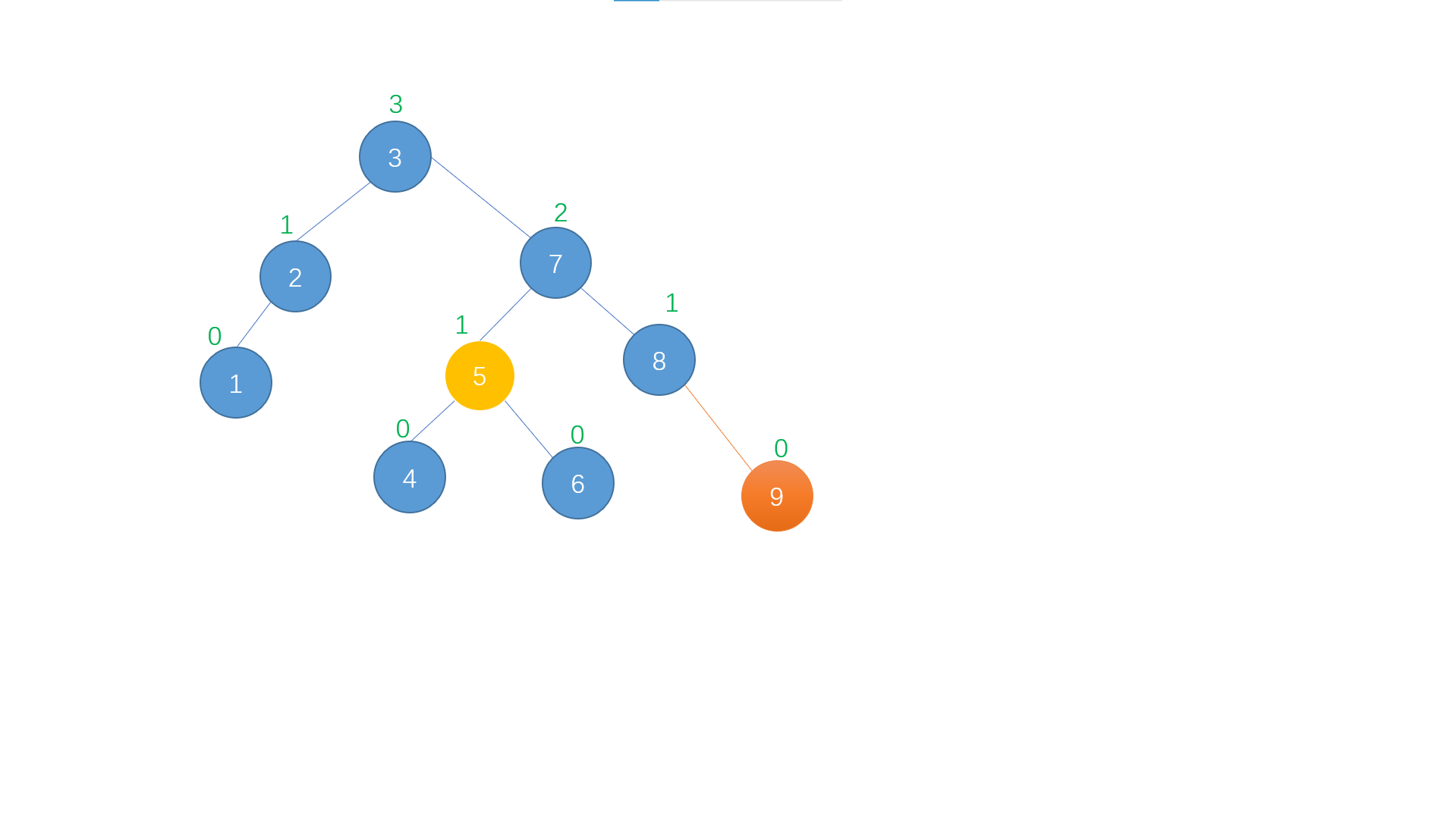
RR insertion means that the "trouble node" is the right child of the "discoverer", that is, the newly inserted node is at the right son of the right son of the nearest "imbalance" node.
At this time, we only operate on the "discoverer" and the nodes on its path to the "trouble node", first pick them out separately, and then rotate them to the left

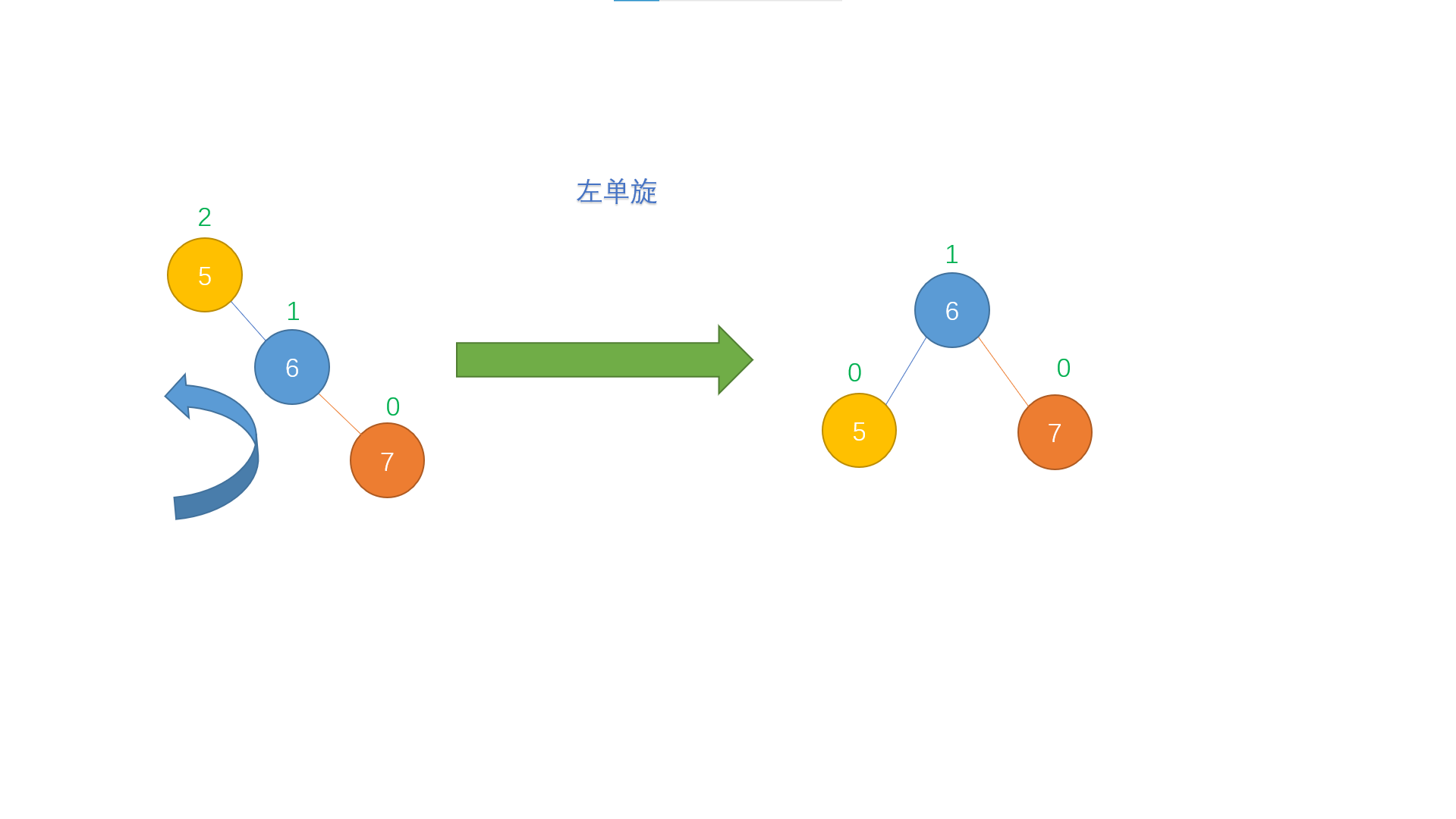
How to understand this process... For example, imagine that these three nodes are three big apples growing on a branch. You cut off the branch, then tie a knot on node 6 and tie it back to the tree. In this way, child node 5 and node 7 naturally sag under the action of gravity and become the left and right children of node 6. Let's see the effect of tying the apple back

In this way, the unbalanced tree is successfully restored to balance.
But this is only a relatively simple case in RR insertion. Try to think about it. In the process of left single rotation, the "discoverer" replaces the position of the node of the left son of the right child. What if the right child of the "discoverer" has a left son? Where will the left son of the right child go?

As shown in the figure above, when the left son of the discoverer's right child is not empty, we only need to turn the left son of the right child into the discoverer's right son while rotating

In short, left single rotation is a process of turning the discoverer node into the left child node of its right child, and letting the right child of the discoverer replace the original position of the discoverer. In this process, if the left son of the discoverer's right child is not empty, we only need to turn the left son of the right child into the right son of the discoverer while rotating.

PS: we should pay attention to the sequence in the process of left single rotation. In the process of left single rotation, we should first obtain the right child of the discoverer, then insert the left son of the right child into the position of the discoverer's right child, then insert the discoverer into the position of the left son of the right child, and finally return to the position of the right child so that the right child can replace the position of the original discoverer.

The code implementation of RR insertion (left single rotation) is as follows:

//RR insertion (left single rotation) 
AVLTree Right_Right_rotation(AVLTree root)
{
	AVLTree Right_Chlid;
	
	Right_Chlid=root->Rightchild;//Take out the right child of the discoverer first 
	root->Rightchild=Right_Chlid->Leftchild;//Then let the right son of "discoverer" point to the left son of his original right child 
	Right_Chlid->Leftchild=root;//Let him become the left son of the original right child 
	
	root->Height=MaxHeight(GetHeight(root->Leftchild),GetHeight(root->Rightchild))+1;//Update the height of the original discoverer 
	Right_Chlid->Height=MaxHeight(GetHeight(Right_Chlid->Leftchild),GetHeight(Right_Chlid->Rightchild))+1;//Update the height of the original "discoverer" right child 
	
	return Right_Chlid;//Return to the right child to replace the original discoverer 
}

LL insertion (right single rotation)

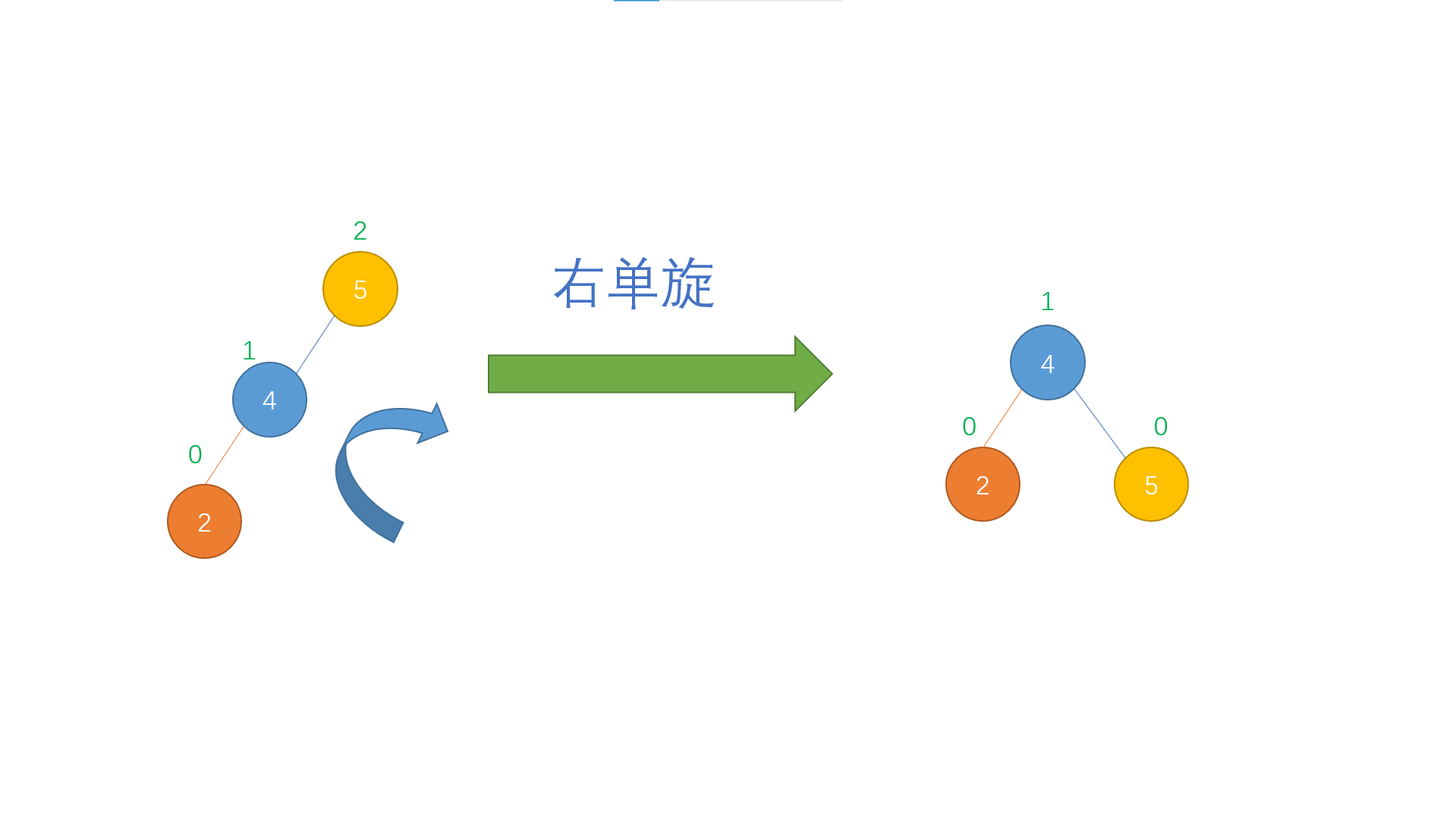
LL insertion (right single rotation) is a mirror operation of RR insertion (left single rotation). As long as some operations of RR insertion (left single rotation) above are reversed, it is mainly an operation for "discoverer" and its left child. An example is shown in the figure below

As shown in the figure, when the trouble node is in the position of the left child of the discoverer's left child, it is called LL insertion. In order to restore its balance, we perform a right single rotation operation on it

Of course, in the process of right single rotation, we should also pay attention to whether the right son of the discoverer's left child is empty,

If the right son of the left child is not empty, insert it into the position of the discoverer's left child.

PS: in fact, we don't need to judge whether the right son of the left child is empty or not. No matter whether it is empty or not, just insert it directly into the position of the left child of the discoverer
In a word, right single rotation is a process of turning the discoverer into the right son of his left child, and the right son of his left child into the left son of the discoverer, and returning the address of the discoverer's original left child to replace the discoverer's original position in the tree.

The code implementation of LL insertion (right single rotation) is as follows:

//LL insertion (right single rotation) 
AVLTree Left_Left_rotation(AVLTree root)
{
	AVLTree Left_Chlid;
	Left_Chlid=root->Leftchild;//Take out the left child of the discoverer first
	root->Leftchild=Left_Chlid->Rightchild;//Then let the left son of "discoverer" point to the right son of his original left child 
	Left_Chlid->Rightchild=root;//Let him become the right son of the original left child 
	
	root->Height=MaxHeight(GetHeight(root->Leftchild),GetHeight(root->Rightchild))+1;//Update the height of the original discoverer 
	Left_Chlid->Height=MaxHeight(GetHeight(Left_Chlid->Leftchild),GetHeight(Left_Chlid->Rightchild))+1;//Update the height of the left child of the original "discoverer" 
	
	return Left_Chlid;//Return to the left child to replace the original discoverer 
}

RL insertion (right left double rotation)

Let's go back to the example at the beginning. What if the trouble node was not the right son of the discoverer's right child, but the left son of the right child

When the troublesome node is the left son of the right child of the discoverer node, this situation is called RL insertion. We need to perform right and left double rotation operation on the discoverer (in fact, the right single rotation is the action on the right child of the discoverer, and the left single rotation is the action on the discoverer). The operation sequence is as follows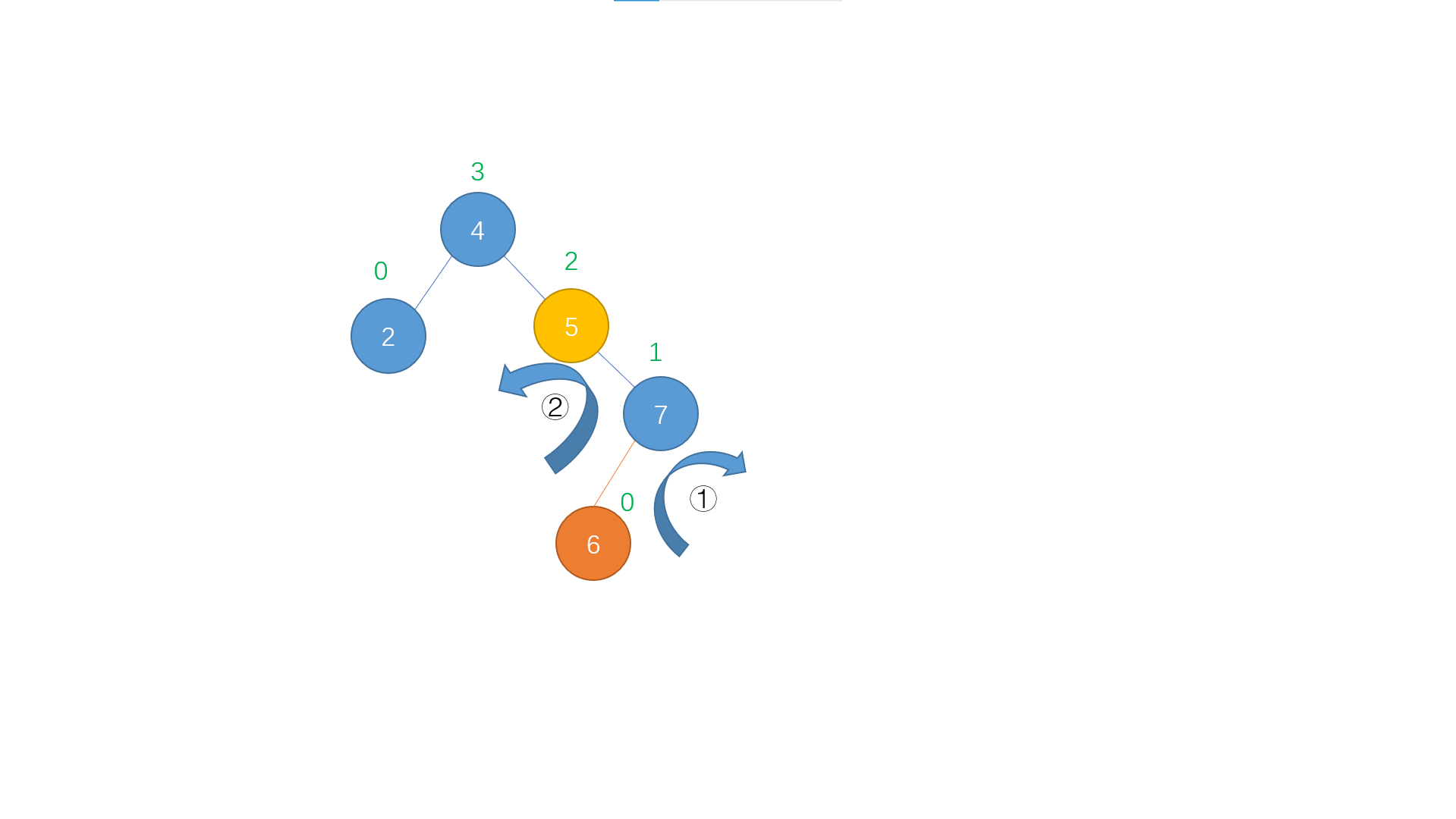First perform right single rotation on the right child of the discoverer node, so that the sub tree becomes the case of RR insertion

Since it becomes the case of RR insertion, the left single rotation operation is performed on the discoverer

Through the above two steps, we successfully balance the unbalanced tree with RL insertion!

In short, right left double rotation is a process of right single rotation on the right child of the discoverer, and then left single rotation on the discoverer.
PS: since we have finished typing the left and right single rotation codes, the code of double rotation operation is simpler..

The code implementation of RL insertion (right left double rotation) is as follows:

/*RL Insert (right and left double rotation)*/ 
AVLTree Right_Left_rotation(AVLTree root)
{
	root->Rightchild=Left_Left_rotation(root->Rightchild);//First perform right single rotation on its right child 
	
	return Right_Right_rotation(root);//Then perform left single rotation on the discoverer 
}

LR insertion (left and right double rotation)

Finally, let's talk about LR insertion. LR insertion refers to the position of the trouble node on the right son of the discoverer's left child, as shown in the following figure

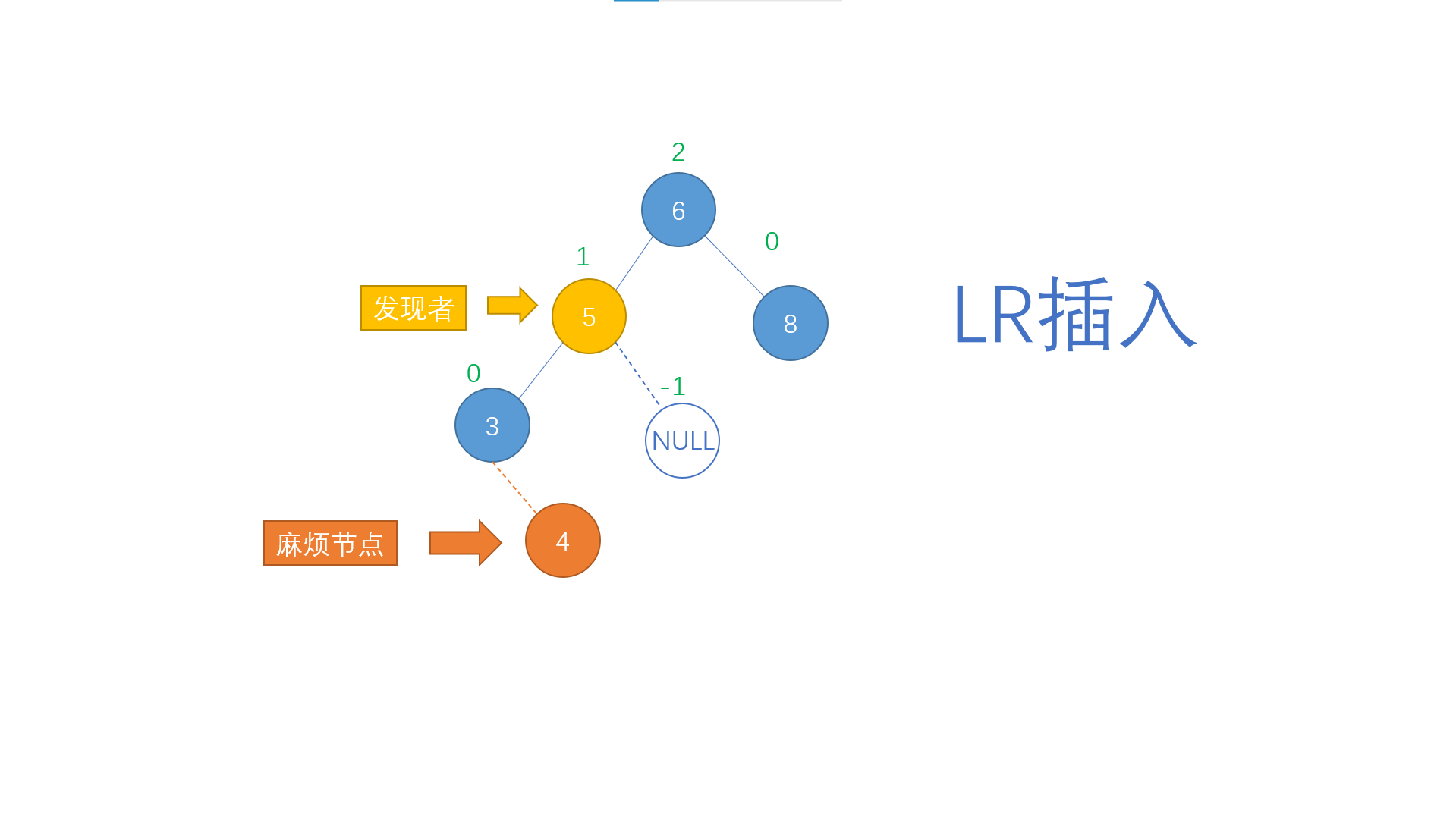
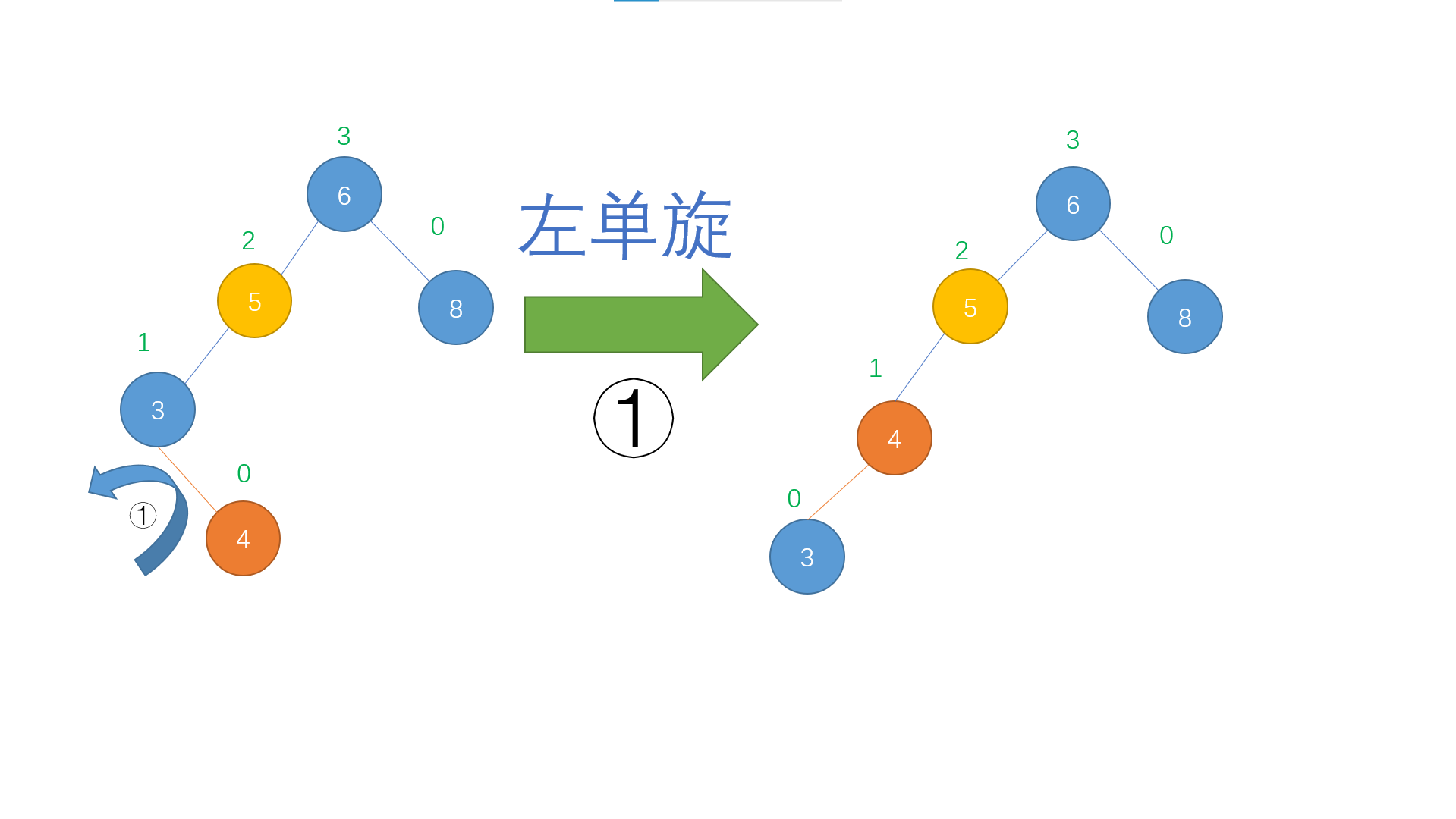
In this case, the operation to be carried out is similar to that of RL insertion. First, carry out left single rotation on the left child of the discoverer to turn it into LL insertion

Finally, right single rotation was performed on the discoverer

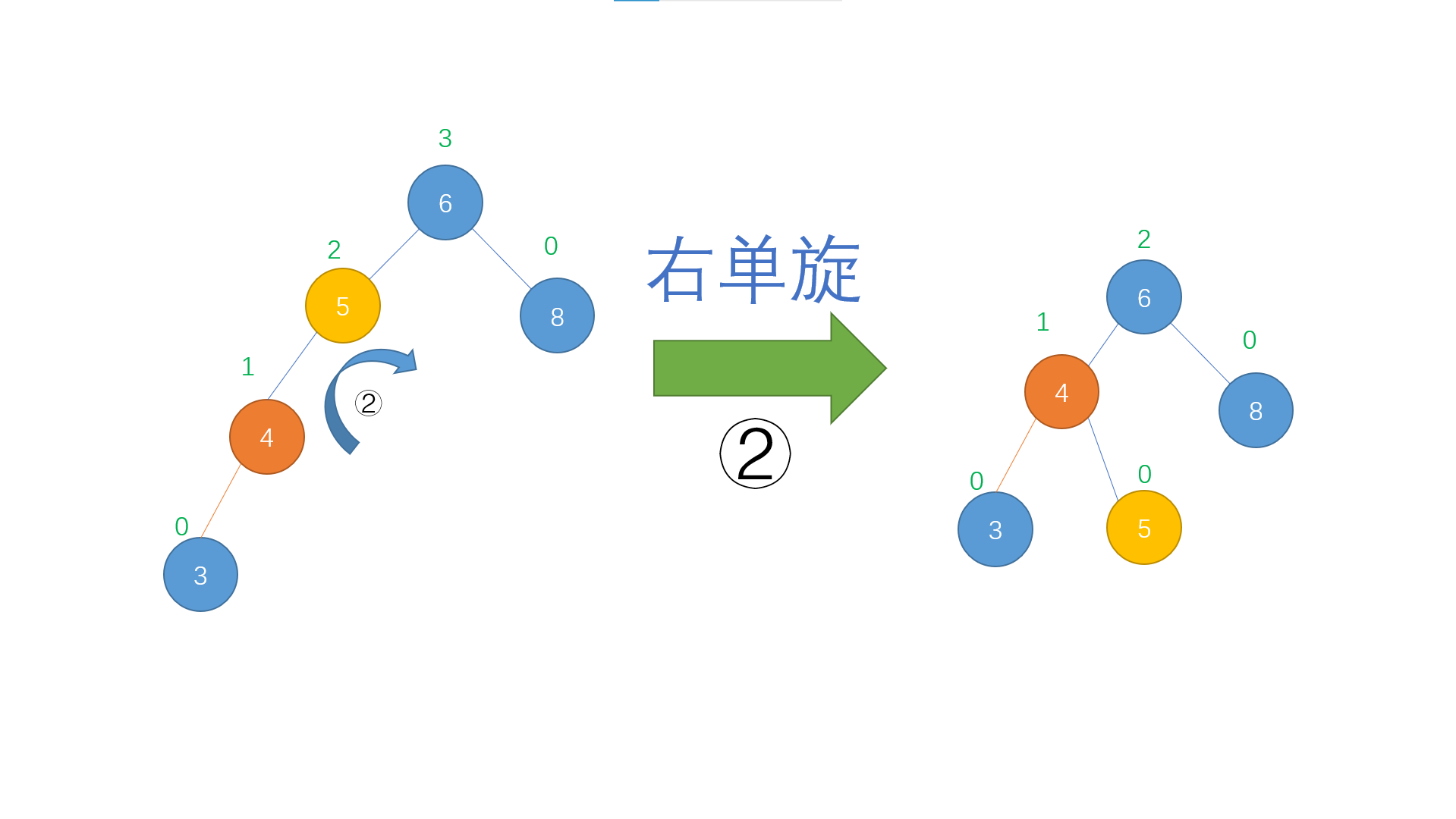
The imbalance in the case of LR insertion is thus restored by us through left-right double rotation.

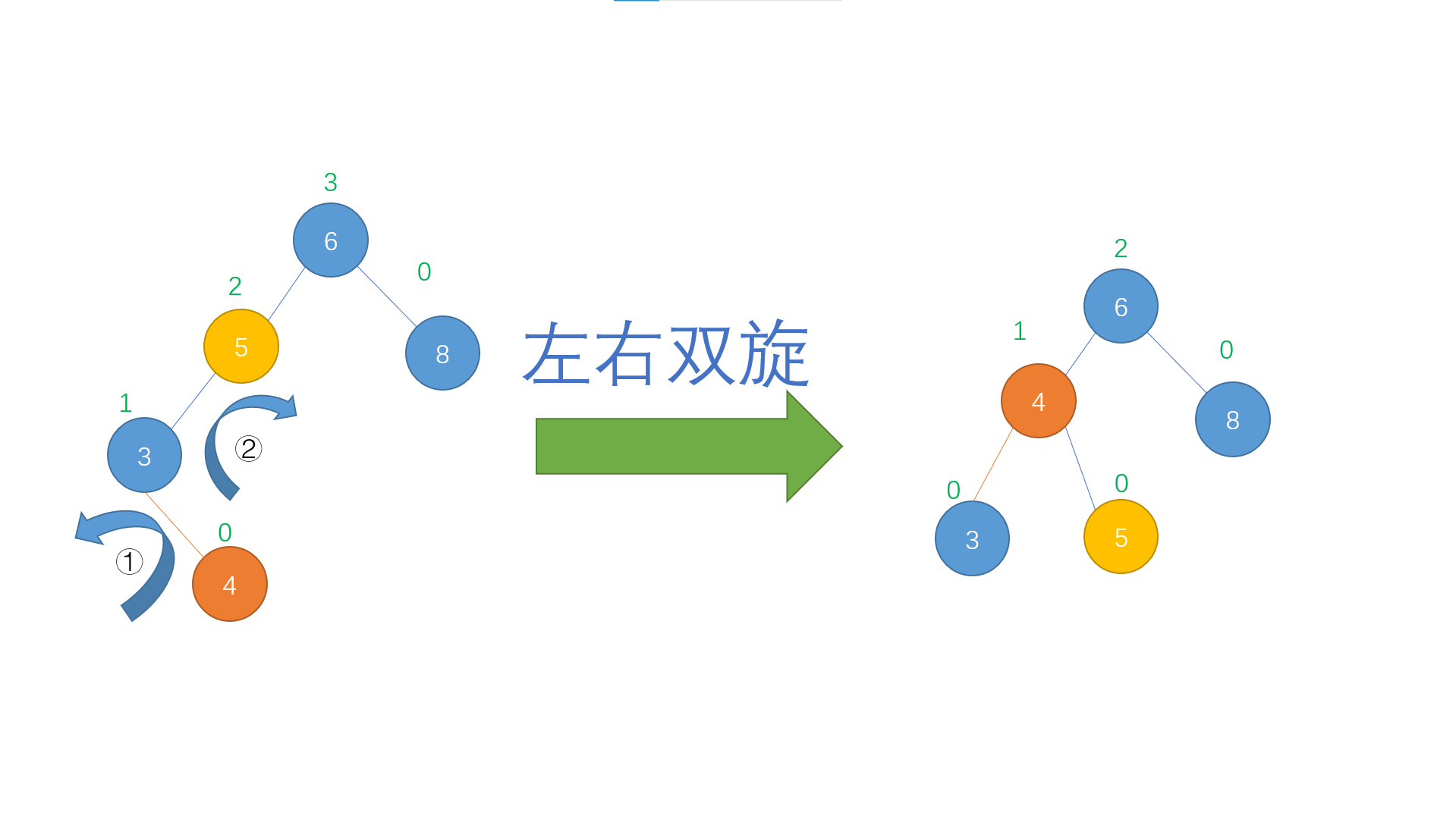
In short, left-right double rotation is the operation process of first performing left single rotation on the left child of the discoverer, and then performing right single rotation on the discoverer.

The code implementation of LR insertion (left and right double rotation) is as follows:

/*LR Insertion (left and right double rotation)*/ 
AVLTree Left_Right_rotation(AVLTree root)
{
	root->Leftchild=Right_Right_rotation(root->Leftchild);//First perform left single rotation on the left son 
	
	return Left_Left_rotation(root);//Right single spin on the discoverer 
}

insert

The insertion process of AVL tree into a node is similar to that of binary search tree, but there are more balance conditions than binary search tree. Therefore, when writing insertion code, we can appropriately imitate the insertion writing method of binary search tree.
Because our AVL tree strictly controls the depth of the tree (O(log N)), we can boldly use the recursive algorithm here.

The inserted code is implemented as follows:

/*insert data*/
AVLTree Insert(AVLTree root,int x)
{
	AVLTree Tree=root;//Get node address 
	if(root==NULL) //When the zero pointer is passed in, it indicates that the appropriate position has been found 
	{
		Tree=(AVLTree)malloc(sizeof(struct AVLTREE));
		Tree->Data=x;
		Tree->Height=0;
		Tree->Leftchild=Tree->Rightchild=NULL;
	} 
	else //When a suitable position has not been found 
	{
		if(x<Tree->Data)//When the data to be inserted is smaller than the value of the current node, it is inserted into the left subtree 
		{
			Tree->Leftchild=Insert(Tree->Leftchild,x);//Insert it into the left subtree 
			if(GetHeight(Tree->Leftchild)-GetHeight(Tree->Rightchild)==2)//If this node is the "discoverer" after the insertion is completed (the node whose difference between the left and right subtrees is just 2) 
			{
				if(x<Tree->Leftchild->Data)//If the data to be inserted is smaller than its left son, it means that the "trouble node" (the newly inserted node that causes the balance to be broken) is on the left of its left son 
					Tree=Left_Left_rotation(Tree);//Left (LL) insertion and right single rotation 
			    else
			    	Tree=Left_Right_rotation(Tree);	//Left and right (LR) insertion, left and right double rotation for this node	
			}	 	
		}
		else if(x==Tree->Data)//When the data to be inserted is the same as the value of the current node 
			printf("Duplicate value!!\n");
		else if(x>Tree->Data)//When the data to be inserted is larger than the data of the current node, insert it into the right subtree 
		{
			Tree->Rightchild=Insert(Tree->Rightchild,x);//Insert it into the right subtree 
			if(GetHeight(Tree->Rightchild)-GetHeight(Tree->Leftchild)==2)//If the node is "discoverer" after insertion 
			{
				if(x>Tree->Rightchild->Data) //To insert data larger than the right son of the "discoverer", the "trouble node" is on the right of its right son 
					Tree=Right_Right_rotation(Tree);//Right right (RR) insertion makes left single rotation for this node 
				else
					Tree=Right_Left_rotation(Tree);//Right and left insertion is left-right double rotation 
			}
		}	
	}
	Tree->Height=MaxHeight(GetHeight(Tree->Leftchild),GetHeight(Tree->Rightchild))+1;//Update the height of path nodes after insertion or balancing 
	    return Tree;
}

In order to help understand this recursive code, try to imagine that a whole AVL tree is regarded as a huge carton. In this large carton (root node), there are two smaller cartons (left and right children). Each carton can hold two smaller cartons at most, and each carton has its own value, You should compare the value on the carton you want to put with the value on the carton you open. If your value is smaller, put it on the left side of the carton, and if the value is larger, put it on the right side of the carton. If there is a carton in the corresponding position, open the carton and continue to compare until you find a space suitable for your carton, Then you put your carton in that position (insert). When you put down your cartons, you need to close the cartons opened in front one by one from the inside to the outside. In the process of closing, you also need to check whether the gap between the two boxes in the box with the most boxes is greater than 1. If it is greater than 1, the box with more boxes will be processed (rotated).

delete

The deletion operation of AVL tree is similar to that of binary search tree. Compare the value to be deleted with the value of the node. If it is smaller than the node, delete it to the left subtree, if it is larger than the node, delete it to the right subtree, and delete it if it is the same size. If the deletion has not been completed until the node becomes NULL, it indicates that the target is not in the tree.
There are four types of target nodes to delete (plus five types that are not in the tree). Leaf nodes without sons, only left sons or right sons, or nodes with both left and right sons

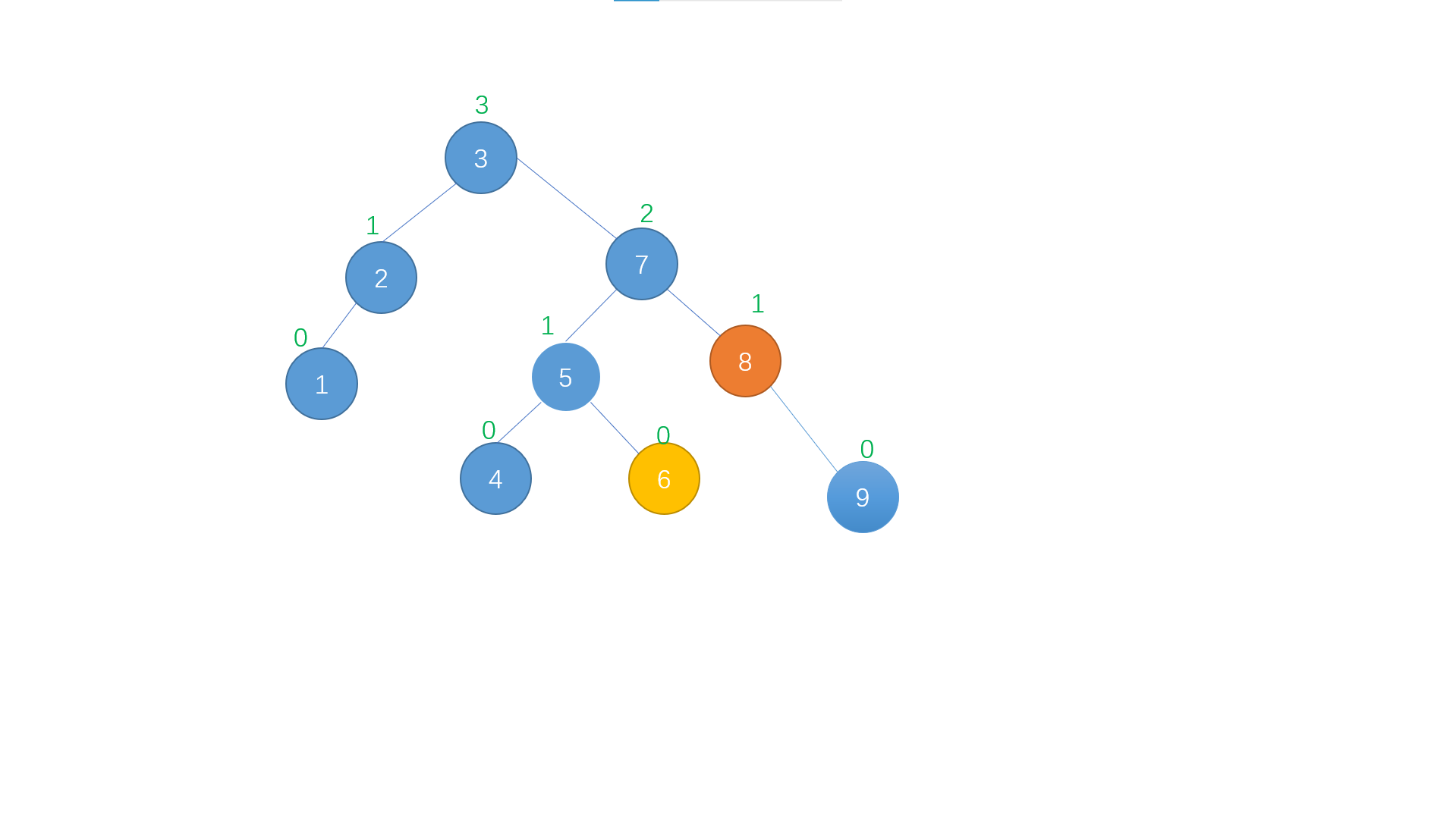
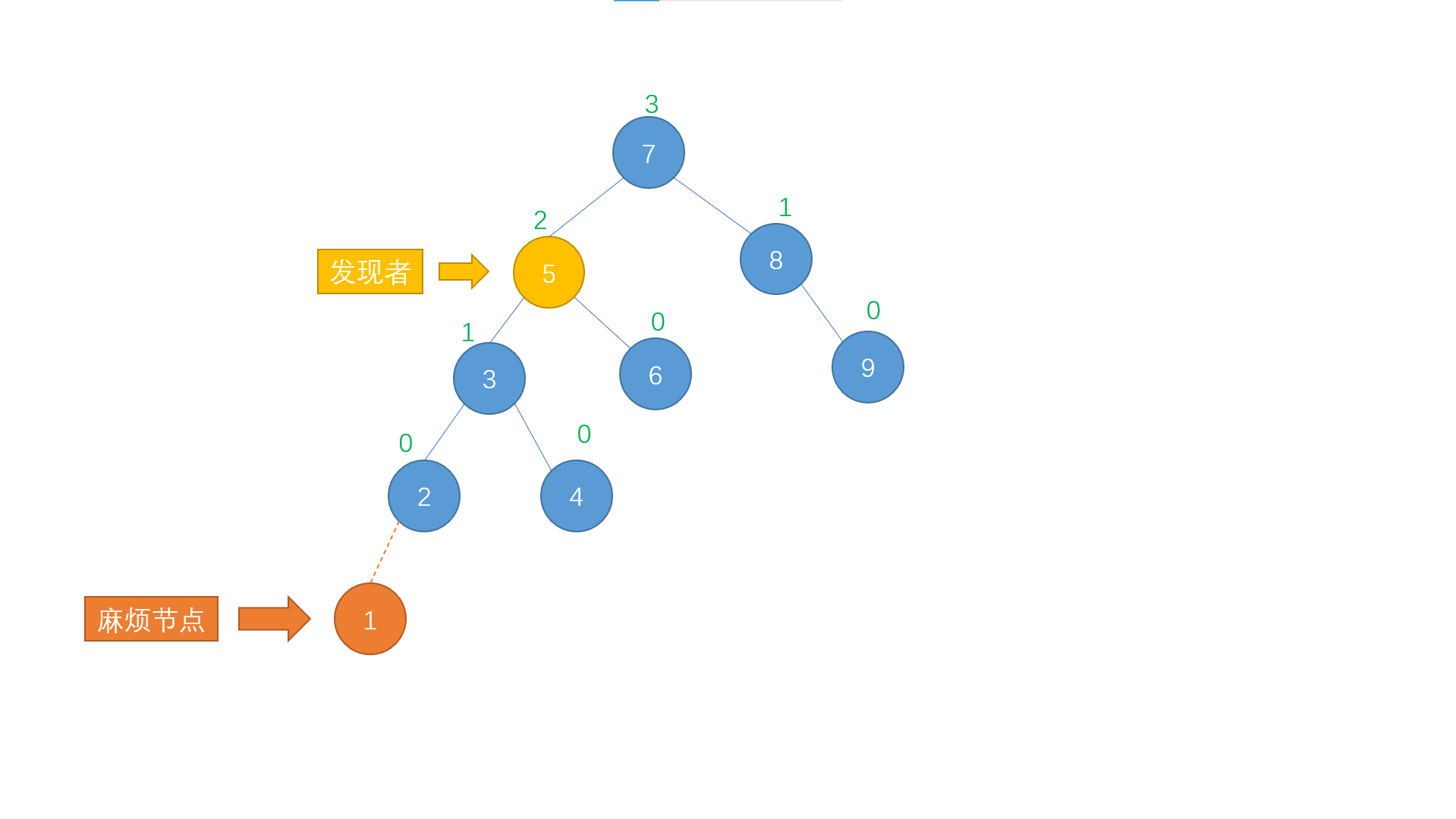
It is very simple to delete nodes with only one or no sons like the one above. You can directly delete and return the "only child", but if we want to delete nodes with both sons like the following, it will be a little troublesome

Node 7 in the figure above can be described as a "traffic fortress". Deleting the whole tree rashly will be unbalanced and difficult to recover again, so we can't operate it by deleting it. See if there are any nodes in its subtree that can replace it? Well, the answer is yes. 6 and 8 are good. Look, how suitable they are

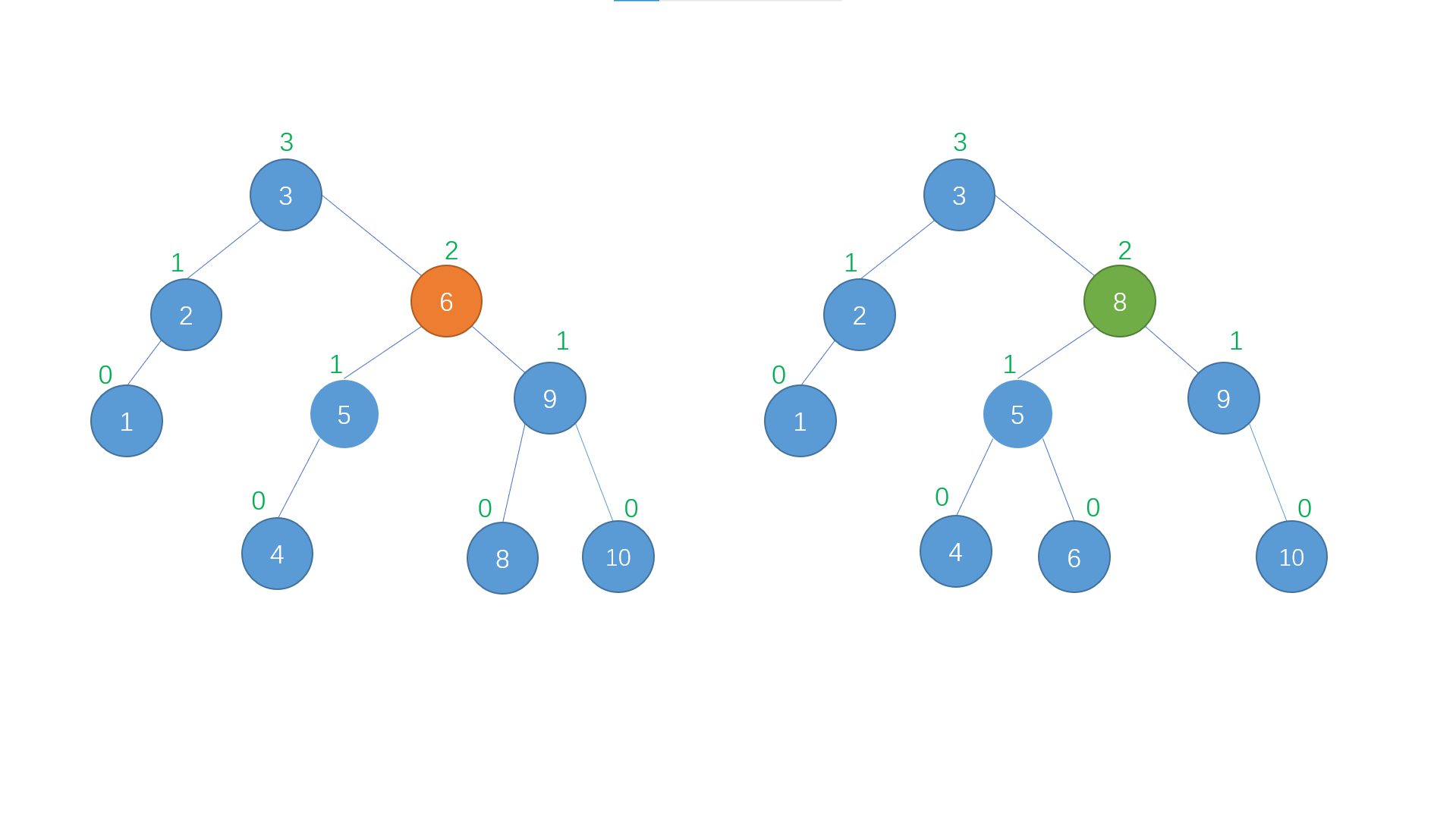
6 and 8 are the largest node of the left subtree and the smallest node of the right subtree of the target node, respectively

Therefore, these two can be used to replace the target node. Here, we arbitrarily choose the minimum value of the right subtree to replace the target node.
So we have to have a function to get the smallest node,

The function to obtain the minimum node is as follows:

*Get minimum node*/ 
AVLTree GetMin(AVLTree root)
{
	if(root->Leftchild!=NULL)//If its left son is not NULL, it recurses all the way to the left 
	return GetMin(root->Leftchild);
	else
	return root;
}

The deleted code is implemented as follows:

/*Delete node*/
AVLTree Delete(AVLTree root,int x)
{
	AVLTree MinTree;//The youngest tree to store the right son 
	if(!root) printf("The data was not found!\n"); 
	
	if(x<root->Data)//If the target data is smaller than the current node, delete it to its left subtree 
		root->Leftchild=Delete(root->Leftchild,x); 
	else if(x>root->Data)//If the target data is larger than the current node, delete it to its right subtree 
	    root->Rightchild=Delete(root->Rightchild,x);
	else if(root->Leftchild&&root->Rightchild)//The node to be deleted is found, and it has both left and right sons 
	{
		MinTree=GetMin(root->Rightchild);//Get the minimum value of the right subtree of the node 
		root->Data=MinTree->Data;//Replace the data of this node with the minimum value of the right subtree
		root->Rightchild=Delete(root->Rightchild,root->Data);//Then delete the minimum value of the right subtree 
	}
	else//The node to be deleted was found, and its left and right sons are incomplete 
	{
		MinTree=root;//First store the location of the node 
		if(!root->Leftchild)//If its left node is NULL, it is replaced by its right child 
		root=root->Rightchild;
		else if(!root->Rightchild)//If its right son is empty, it is replaced by its left son 
		root=root->Leftchild;
		free(MinTree);//Release old node 
	}
	return root;
}

ergodic

There are four traversal modes: front, middle and back and sequence traversal. Among these four traversal modes, we mainly talk about the more difficult sequence traversal
What is sequence traversal? Hierarchical traversal is to traverse the binary tree layer by layer, from left to right.

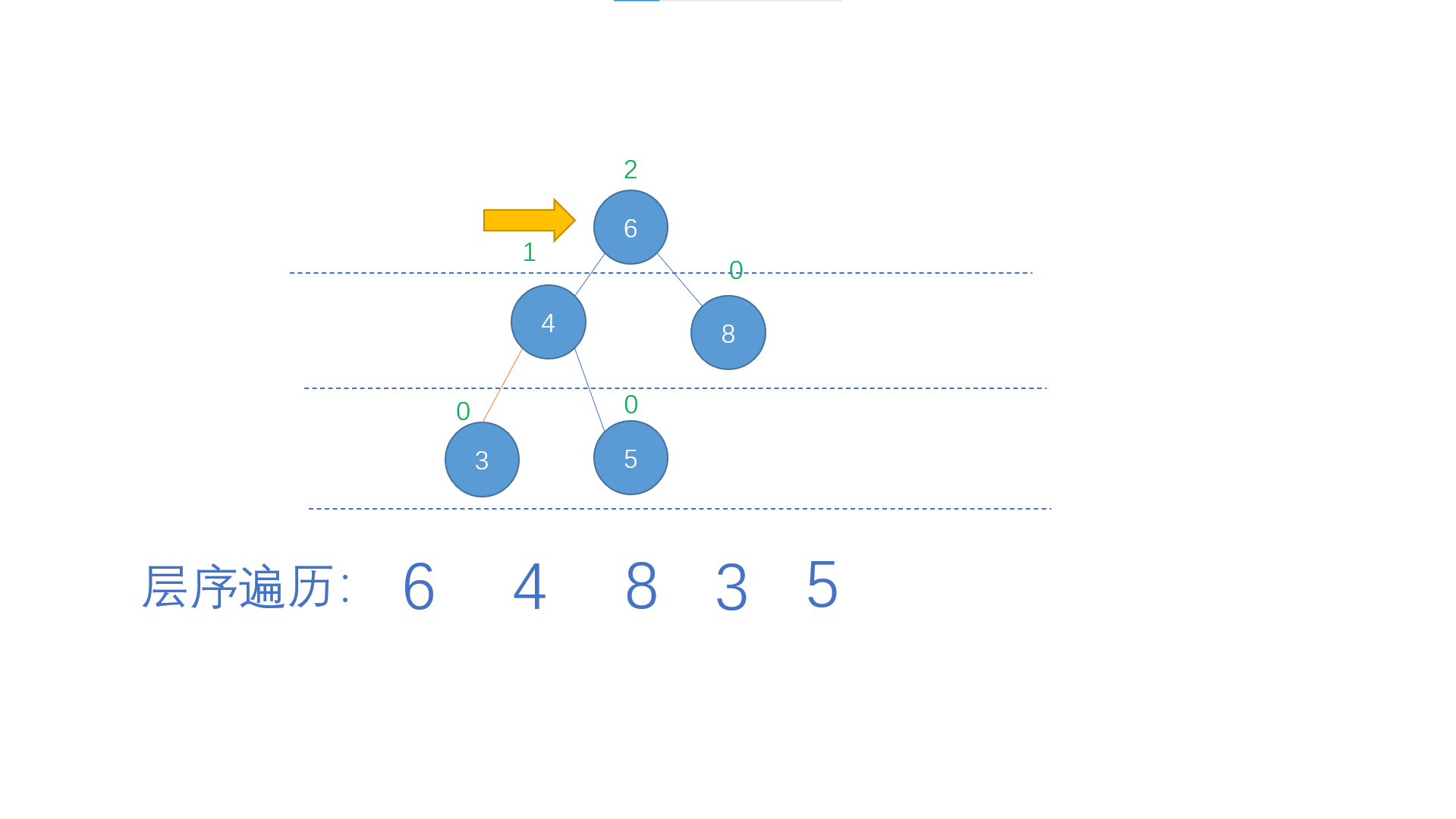
So how do we make the binary trees of one layer to one layer in order?

Yes, we can use the queue!
The steps are shown in the figure below

We first create a circular queue, and now put the root node into the queue. For each node out of the queue, we will queue the non empty left and right sons of this node in order. In this way, we have realized hierarchical traversal!

The hierarchical traversal code is implemented as follows:

/*Hierarchical traversal of AVL tree*/ 
void LevelTree(AVLTree root)
{
	AVLTree Queue[Maxsize],Tree;//A queue of left and right sons 
	int rear=0,front=0;//Initialize queue header and tail 
	if(root!=NULL)//If the root node is not NULL, the root node will be stored in the queue first 
		Queue[++rear]=root;
		
		while(front!=rear)//When the head and tail are the same, the queue is empty 
		{
			front=(front+1)%Maxsize;//Let the queue header point to the node to be dequeued first 
			Tree=Queue[front];//Take out the node to be dequeued 
			printf("%d ",Tree->Data);//Its output value 
			
			/*Put their left and right sons in the queue in order*/ 
			if(Tree->Leftchild!=NULL)//Put the left son first 
			{
				rear=(rear+1)%Maxsize;//Move one position back at the end of the team 
			    Queue[rear]=Tree->Leftchild;//Put in queue 
			}
			if(Tree->Rightchild!=NULL)//Then put in the right son 
			{
				rear=(rear+1)%Maxsize;//Move one position back at the end of the team
			    Queue[rear]=Tree->Rightchild;//Put in queue 	
			}
		}
}

The first, middle and last traversal codes are as follows:

/*Preorder traversal*/
void PreOrder(AVLTree root)
{
	if(!root) return;//If the tree is empty, exit 
	else
	{
		printf("%d ",root->Data);
		PreOrder(root->Leftchild);
    	PreOrder(root->Rightchild);
	}
}

/*Middle order traversal*/ 
void InOrder(AVLTree root)
{
	if(!root) return;//If the tree is empty, exit 
	else
	{
		InOrder(root->Leftchild); 
		printf("%d ",root->Data);
    	InOrder(root->Rightchild);
	}
}

/*Postorder traversal*/
void PostOrder(AVLTree root)
{
	if(!root) return;//If the tree is empty, exit 
	else
	{
		PostOrder(root->Leftchild);
   	    PostOrder(root->Rightchild);
   	    printf("%d ",root->Data);
	}
}

Complete code

#include<stdio.h>
#include<stdlib.h>
#define Maxsize 20

typedef struct AVLTREE
{
	int Data;//Store data 
	int Height;//height 
	struct AVLTREE *Leftchild;//Left subtree 
	struct AVLTREE *Rightchild;//Right subtree 
}*AVLTree;


/*menu*/ 
void Menu(void);
/*Sequence traversal tree*/
void LevelTree(AVLTree root);
/*insert data*/
AVLTree Insert(AVLTree root,int x);
/*Delete data*/
AVLTree Delete(AVLTree root,int x);
/*Find minimum*/
AVLTree GetMin(AVLTree root);
/*Right single rotation*/
AVLTree Left_Left_rotation(AVLTree root);
/*Sinistral*/
AVLTree Right_Right_rotation(AVLTree root);
/*Left and right double rotation*/ 
AVLTree Left_Right_rotation(AVLTree root);
/*Right left double spin*/ 
AVLTree Right_Left_rotation(AVLTree root);
/*Preorder traversal */ 
void PreOrder(AVLTree root);
/*Middle order traversal*/
void InOrder(AVLTree root);
/*Postorder traversal*/
void PostOrder(AVLTree root);
/*Compare the height of the tree*/
int MaxHeight(int Left,int Right);
/*Get the height of the tree*/
int GetHeight(AVLTree root);


int main(void)
{
	AVLTree root=NULL;
	int tragger;
	int data=0;
	
	while(1)
	{
		Menu();
		scanf("%d",&tragger);
		
		switch(tragger)
		{
			case 1:
				    printf("Please enter data (enter)-1 End):\n");
					scanf("%d",&data);
					while(data!=-1)
					{
						root=Insert(root,data); 
						printf("Please enter data (enter)-1 End):\n");
						scanf("%d",&data);	
					}
					break;
			case 2:  printf("level traversal :");
				     LevelTree(root);
				     break;
				     
			case 3: printf("Preorder traversal:");
			        PreOrder(root);
			          break;
			case 4: printf("Middle order traversal:");
					InOrder(root);
			        break;
			case 5: printf("Postorder traversal:");
					 PostOrder(root);
			        break;
			case 6:  printf("Please enter the data to delete:\n");
			          scanf("%d",&data);
			          root=Delete(root,data);
			          break;
			case 0:
				    return 0;
		}
	}

	return 0;
}

void Menu(void)
{
	printf("\n///");
	printf("\n// 1. Insert data: / / ");
	printf("\n// 2. Sequence traversal binary tree: / / ");
    printf("\n// 3. Pre order traversal of binary tree: / / ");
    printf("\n// 4. Traversing binary tree in middle order: / / ");
    printf("\n// 5. Post order traversal of binary tree: / / ");
    printf("\n// / / (6). Delete data: / /);
	printf("\n// 0. Exit: / / ");
    printf("\n/\n");
	
}

/*insert data*/
AVLTree Insert(AVLTree root,int x)
{
	AVLTree Tree=root;//Get node address 
	if(root==NULL) //When the zero pointer is passed in, it indicates that the appropriate position has been found 
	{
		Tree=(AVLTree)malloc(sizeof(struct AVLTREE));
		Tree->Data=x;
		Tree->Height=0;
		Tree->Leftchild=Tree->Rightchild=NULL;
	} 
	else //When a suitable position has not been found 
	{
		if(x<Tree->Data)//When the data to be inserted is smaller than the value of the current node, it is inserted into the left subtree 
		{
			Tree->Leftchild=Insert(Tree->Leftchild,x);//Insert it into the left subtree 
			if(GetHeight(Tree->Leftchild)-GetHeight(Tree->Rightchild)==2)//If this node is the "discoverer" after the insertion is completed (the node whose difference between the left and right subtrees is just 2) 
			{
				if(x<Tree->Leftchild->Data)//If the data to be inserted is smaller than its left son, it means that the "trouble node" (the newly inserted node that causes the balance to be broken) is on the left of its left son 
					Tree=Left_Left_rotation(Tree);//Left (LL) insertion and right single rotation 
			    else
			    	Tree=Left_Right_rotation(Tree);	//Left and right (LR) insertion, left and right double rotation for this node	
			}	 	
		}
		else if(x==Tree->Data)//When the data to be inserted is the same as the value of the current node 
			printf("Duplicate value!!\n");
		else if(x>Tree->Data)//When the data to be inserted is larger than the data of the current node, insert it into the right subtree 
		{
			Tree->Rightchild=Insert(Tree->Rightchild,x);//Insert it into the right subtree 
			if(GetHeight(Tree->Rightchild)-GetHeight(Tree->Leftchild)==2)//If the node is "discoverer" after insertion 
			{
				if(x>Tree->Rightchild->Data) //To insert data larger than the right son of the "discoverer", the "trouble node" is on the right of its right son 
					Tree=Right_Right_rotation(Tree);//Right right (RR) insertion makes left single rotation for this node 
				else
					Tree=Right_Left_rotation(Tree);//Right and left insertion is left-right double rotation 
			}
		}	
	}
	Tree->Height=MaxHeight(GetHeight(Tree->Leftchild),GetHeight(Tree->Rightchild))+1;//Update the height of path nodes after insertion or balancing 
	    return Tree;
}


/*Hierarchical traversal of AVL tree*/ 
void LevelTree(AVLTree root)
{
	AVLTree Queue[Maxsize],Tree;//A queue of left and right sons 
	int rear=0,front=0;//Initialize queue header and tail 
	if(root!=NULL)//If the root node is not NULL, the root node will be stored in the queue first 
		Queue[++rear]=root;
		
		while(front!=rear)//When the head and tail are the same, the queue is empty 
		{
			front=(front+1)%Maxsize;//Let the queue header point to the node to be dequeued first 
			Tree=Queue[front];//Take out the node to be dequeued 
			printf("%d ",Tree->Data);//Its output value 
			
			/*Put their left and right sons in the queue in order*/ 
			if(Tree->Leftchild!=NULL)//Put the left son first 
			{
				rear=(rear+1)%Maxsize;//Move one position back at the end of the team 
			    Queue[rear]=Tree->Leftchild;//Put in queue 
			}
			if(Tree->Rightchild!=NULL)//Then put in the right son 
			{
				rear=(rear+1)%Maxsize;//Move one position back at the end of the team
			    Queue[rear]=Tree->Rightchild;//Put in queue 	
			}
		}
	
}

//Compare the height of the left and right sons 
int MaxHeight(int Left,int Right)
{
	if(Left>Right)
	 return Left;
	else
	 return Right;
}

//Get node height 
int GetHeight(AVLTree root)
{
   if(root==NULL)
	return -1;
   else
    return MaxHeight(GetHeight(root->Leftchild),GetHeight(root->Rightchild))+1;
}

//LL insertion (right single rotation) 
AVLTree Left_Left_rotation(AVLTree root)
{
	AVLTree Left_Chlid;
	Left_Chlid=root->Leftchild;//Take out the left child of the discoverer first 
	root->Leftchild=Left_Chlid->Rightchild;//Then let the left son of "discoverer" point to the right son of his original left child 
	Left_Chlid->Rightchild=root;//Let it become the right son of the original left son 
	
	root->Height=MaxHeight(GetHeight(root->Leftchild),GetHeight(root->Rightchild))+1;//Update the height of the original discoverer 
	Left_Chlid->Height=MaxHeight(GetHeight(Left_Chlid->Leftchild),GetHeight(Left_Chlid->Rightchild))+1;//Update the height of the left child of the original "discoverer" 
	
	return Left_Chlid;//Return to the left child to replace the original discoverer 
}

//RR insertion (left single rotation) 
AVLTree Right_Right_rotation(AVLTree root)
{
	AVLTree Right_Chlid;
	
	Right_Chlid=root->Rightchild;//Take out the right child of the discoverer first 
	root->Rightchild=Right_Chlid->Leftchild;//Then let the right son of "discoverer" point to the left son of his original right child 
	Right_Chlid->Leftchild=root;//Let him become the left son of the original right child 
	
	root->Height=MaxHeight(GetHeight(root->Leftchild),GetHeight(root->Rightchild))+1;//Update the height of the original discoverer 
	Right_Chlid->Height=MaxHeight(GetHeight(Right_Chlid->Leftchild),GetHeight(Right_Chlid->Rightchild))+1;//Update the height of the original "discoverer" right child 
	
	return Right_Chlid;//Return to the right child to replace the original discoverer 
}

/*LR Insertion (left and right double rotation)*/ 
AVLTree Left_Right_rotation(AVLTree root)
{
	root->Leftchild=Right_Right_rotation(root->Leftchild);//First perform left single rotation on the left child 
	
	return Left_Left_rotation(root);//Then right single spin the discoverer 
}

/*RL Insert (right and left double rotation)*/ 
AVLTree Right_Left_rotation(AVLTree root)
{
	root->Rightchild=Left_Left_rotation(root->Rightchild);//First perform right single rotation on its right child 
	
	return Right_Right_rotation(root);//Then perform left single rotation on the discoverer 
}

/*Preorder traversal*/
void PreOrder(AVLTree root)
{
	if(!root) return;//If the tree is empty, exit 
	else
	{
		printf("%d ",root->Data);
		PreOrder(root->Leftchild);
    	PreOrder(root->Rightchild);
	}
}

/*Middle order traversal*/ 
void InOrder(AVLTree root)
{
	if(!root) return;//If the tree is empty, exit 
	else
	{
		InOrder(root->Leftchild); 
		printf("%d ",root->Data);
    	InOrder(root->Rightchild);
	}
}

/*Postorder traversal*/
void PostOrder(AVLTree root)
{
	if(!root) return;//If the tree is empty, exit 
	else
	{
		PostOrder(root->Leftchild);
   	    PostOrder(root->Rightchild);
   	    printf("%d ",root->Data);
	}
}

/*Delete node*/
AVLTree Delete(AVLTree root,int x)
{
	AVLTree MinTree;//The youngest tree to store the right son 
	if(!root) printf("The data was not found!\n"); 
	
	if(x<root->Data)//If the target data is smaller than the current node, delete it to its left subtree 
		root->Leftchild=Delete(root->Leftchild,x); 
	else if(x>root->Data)//If the target data is larger than the current node, delete it to its right subtree 
	    root->Rightchild=Delete(root->Rightchild,x);
	else if(root->Leftchild&&root->Rightchild)//The node to be deleted is found, and it has both left and right sons 
	{
		MinTree=GetMin(root->Rightchild);//Get the minimum value of the right subtree of the node 
		root->Data=MinTree->Data;//Replace the data of this node with the minimum value of the right subtree
		root->Rightchild=Delete(root->Rightchild,root->Data);//Then delete the minimum value of the right subtree 
	}
	else//The node to be deleted was found, and its left and right sons are incomplete 
	{
		MinTree=root;//First store the location of the node 
		if(!root->Leftchild)//If its left node is NULL, it is replaced by its right child 
		root=root->Rightchild;
		else if(!root->Rightchild)//If its right son is empty, it is replaced by its left son 
		root=root->Leftchild;
		free(MinTree);//Release old node 
	}
	return root;
}

/*Get minimum node*/ 
AVLTree GetMin(AVLTree root)
{
	if(root->Leftchild!=NULL)//If its left son is not NULL, it recurses all the way to the left 
	return GetMin(root->Leftchild);
	else
	return root;
}

Code test

Next, let's test the reliability of our code
I started by rolling up a tree

Then we insert it into a tree in the order of "9 8 7 1 3 5 4 6 10 12 15 14 13 16 2 11"

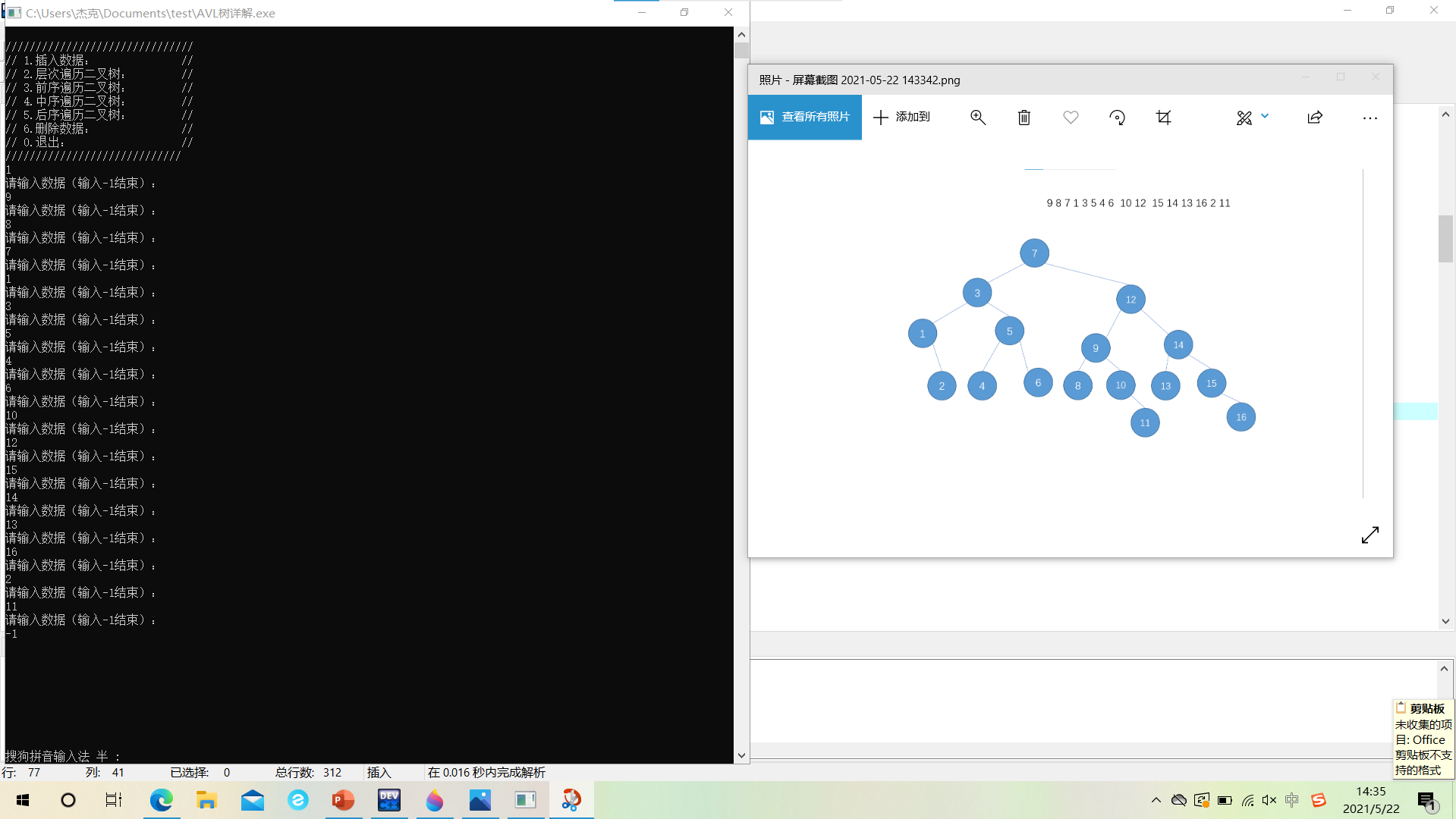
Then traverse it

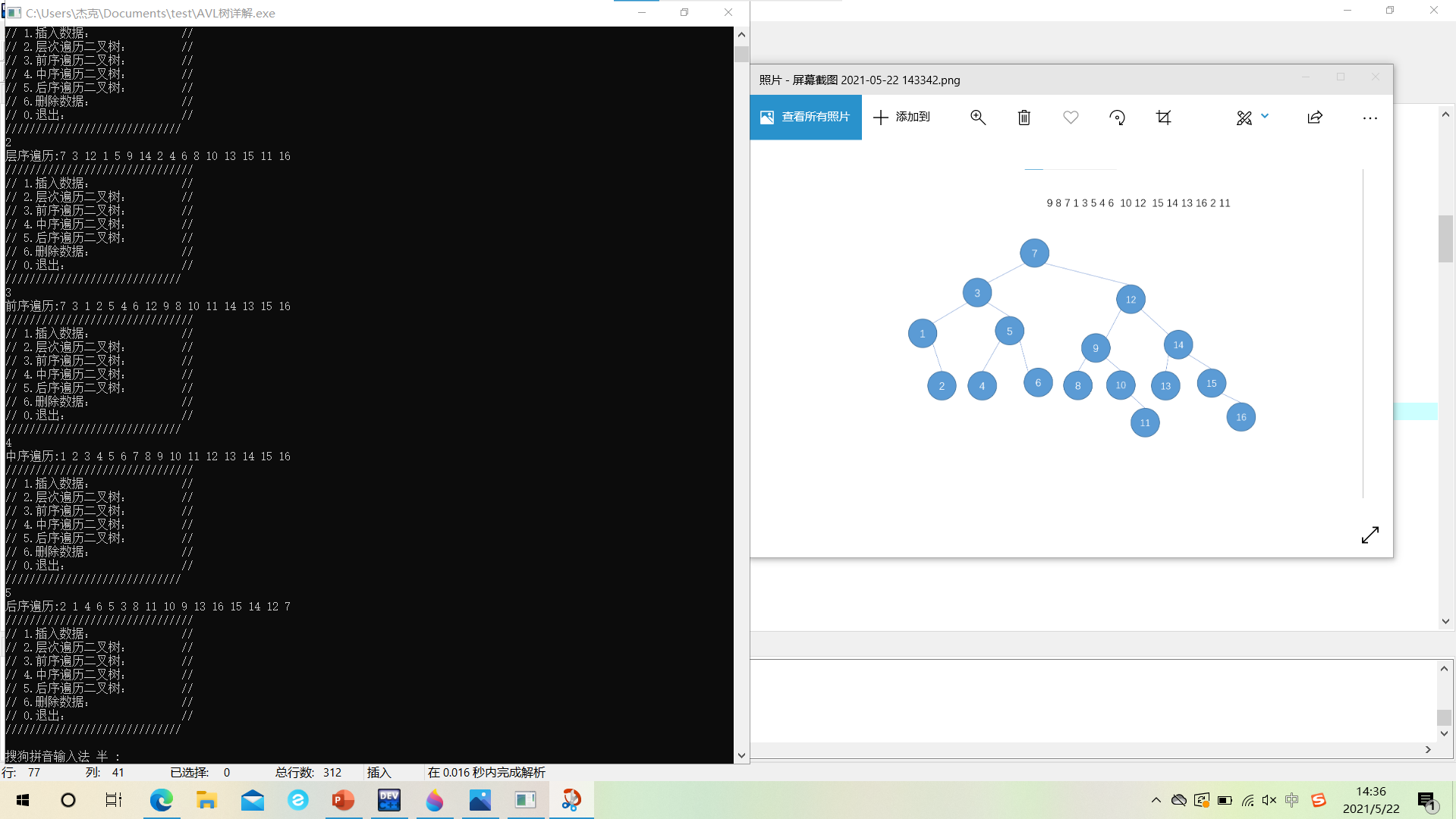
Traversal result
Level traversal: 7,3,12,1,5,9,14,2,4,6,8,10,13,15,11,16
Preorder traversal: 7,3,1,2,5,4,6,12,9,8,10,11,14,13,15,16
Middle order traversal: 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16
Post order traversal: 2,1,4,6,5,3,8,11,10,9,13,16,15,14,12,7
yes! The result is the same as my hand. Pass!
Next, we delete a batch of nodes 12 of cattle to see its results

yes!OK!
Generally speaking, our code is still broad!!!

reference material
Data structure and algorithm analysis C language description [US] by Mark Allen Weiss, translated by Feng Shunxi, China Machine Press
If the sky doesn't die, big brother's blog

Broken thoughts
My God, if we don't update it for more than a month, we will almost lose my whole person.
Now I'm extremely tired,
Lazy to check (ﾟ▽ﾟ *)
If there is anything wrong,
Please also give me your advice
I went to the movies~~
Sprinkle flowers.

Keywords: Algorithm data structure Binary tree

Added by slimsam1 on Wed, 09 Feb 2022 09:01:51 +0200

Programming VIP

AVL tree introduction and detailed explanation of each operation