1. General
AVL tree is the first self balanced binary tree proposed. In AVL tree, the maximum difference between the two subtrees of any node is one, so it is also called height balanced tree. The AVL tree is named after its inventors G.M. Adelson velsky and E.M. Landis. AVL tree species search, insertion and deletion are O (log n) on average and in the worst case. Adding and deleting may need to rebalance the tree through one or more tree rotations. This paper introduces the design idea and basic operation of AVL tree.
2. Basic terms
There are four situations that may lead to the imbalance of binary search tree:
(1) LL: insert a new node into the Left subtree of the Left subtree of the root node, resulting in the balance factor of the root node changing from 1 to 2
(2) RR: insert a new node into the Right subtree of the Right subtree of the root node, resulting in the balance factor of the root node changing from - 1 to - 2
(3) LR: insert a new node into the Right subtree of the Left subtree of the root node, resulting in the balance factor of the root node changing from 1 to 2
(4) RL: insert a new node into the Left subtree of the Right subtree of the root node, resulting in the balance factor of the root node changing from - 1 to - 2
In view of the possible imbalance caused by four situations, it can be balanced by rotation. There are two basic rotations:
(1) Rotate left: rotate the root node to the left child position of the right child (of the root node)
(2) Rotate right: rotate the root node to the right child position of the left child (of the root node)
Basic data structure

typedef struct Node* Tree;
typedef struct Node* Node_t;
typedef Type int;
struct Node{
     Node_t left;
     Node_t right;
     int height;
     Type data;
};
int Height(Node_t node) {
     return node->height;
}

3.1 LL

LL condition needs to be solved by right rotation, as shown in the figure below:

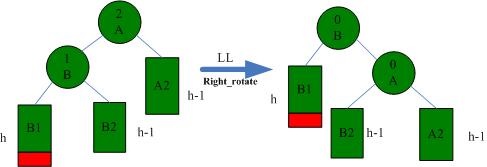
Node_t RightRotate(Node_t a) {
     b = a->left;
     a->left = b->right;
     b->right = a;
     a->height = Max(Height(a->left), Height(a->right));
     b->height = Max(Height(b->left), Height(b->right));
     return b;
}

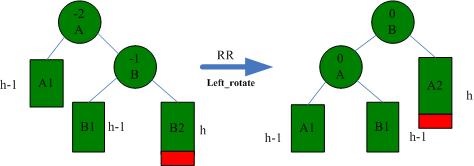
3.2 RR

The RR situation needs to be solved by left rotation, as shown in the figure below:

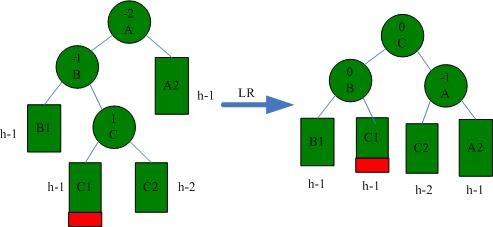
3.3 LR

LR situation needs to be solved by left-right rotation (first B rotates left and then A rotates right), as shown in the following figure:

Node_t LeftRightRotate(Node_t a) {
     a->left = LeftRotate(a->left);
     return RightRotate(a);
}

3.4 RL

RL situation needs to be solved by right and left rotation (first B rotates right, then A rotates left), as shown in the following figure:

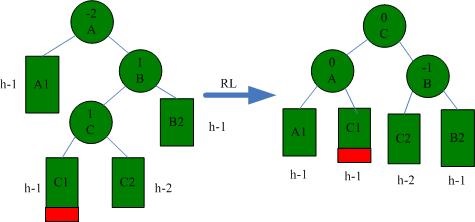
Node_t RightLeftRotate(Node_t a) {
     a->right = RightRotate(a->right);
     return LeftRotate(a);
}

4. Insert and delete AVL number

(1) Insert operation: in fact, it is to adjust the whole tree by using different rotation methods under different circumstances. The specific code is as follows:

Node_t Insert(Type x, Tree t) {
    if(t == NULL) {
        t = NewNode(x);
     } else if(x < t->data) {
         t->left = Insert(t->left);
         if(Height(t->left) - Height(t->right) == 2) {
                if(x < t->left->data) {
                      t = RightRotate(t);
               } else {
                      t = LeftRightRotate(t);
               }
        }
        } else {
               t->right = Insert(t->right);
               if(Height(t->right) - Height(t->left) == 2) {
                     if(x > t->right->data) {
                          t = LeftRotate(t);
                    } else {
                         t = RightLeftRotate(t);
                    }
               }
      }
      t->height = Max(Height(t->left), Height(t->right)) + 1;
      return t;
}

(2) Delete operation: first locate the node to be deleted, then replace the node with the leftmost child of the right child of the node, and readjust the subtree with the node as the root to AVL tree. The specific adjustment method is similar to inserting data. The code is as follows:

Node_t Delete(Type x, Tree t) {
      if(t == NULL) return NULL;
      if(t->data == x) {
            if(t->right == NULL) {
                   Node_t temp = t;
                   t = t->left;
                   free(temp);
            } else {
                  Node_t head = t->right;
                  while(head->left) {
                         head = head->left;
                  }
                  t->data = head->data; //just copy data
                  t->right = Delete(t->data, t->right);
                  t->height = Max(Height(t->left), Height(t->right)) + 1;
         }
         return t;
     } else if(t->data < x) {
            Delete(x, t->right);
            if(t->right) Rotate(x, t->right);
            } else {
                 Delete(x, t->left);
                 if(t->left) Rotate(x, t->left);
            }
            if(t) Rotate(x, t);
}

5. Summary

AVL tree is the earliest self balanced binary tree. Compared with the later balanced binary trees (red black tree, tree, splay tree), it is less used now, but the study of AVL tree is of great significance to understand the common balanced binary trees.