I recommend a free open course of zero sound college. Personally, I think the teacher speaks well. I share it with you: Linux, Nginx, ZeroMQ, MySQL, Redis, fastdfs, MongoDB, ZK, streaming media, CDN, P2P, K8S, Docker, TCP/IP, collaboration, DPDK and other technical contents, learn immediately
Introduction to B-tree
Before talking about the B-tree, let's discuss the difference between memory and disk?
Many friends can more or less say something about this problem
Maybe the first point many friends answer is
1. Fast memory and slow disk
2. After power failure, the data disappears and the disk is permanently stored
In this simple process, three-level storage, register, memory and disk are built
Registers are small and fast, then memory and then disk;
If this concept is clear, let's talk about it again: when we access memory, we have a few instructions to explain why we need to start talking about B-tree from this place. Otherwise, we certainly don't know why B-tree and B + tree are only suitable for use on disk and not in memory
mov eax [0008h] this instruction refers to putting a value in the memory into the register. The cpu can access all the values in the memory through the instruction, and we can access any position in the memory through the cpu instruction; If there is no data in the memory, it will cause a page missing exception if it is not hit. For example, when we access the disk and access a file, the file is very large. When accessing data, it will first add the file to the memory. If it is found that there is no data in the memory during the access, it will cause a page missing action, What will this missing page action send? I will go to the disk for addressing. During the addressing process, please note that what we see here may be three boxes. The intuitive feeling for you is three boxes. It is difficult to feel why the disk is slower than the memory? Where is the slow? Without an intuitive feeling, the memory can be accessed through the instructions of the cpu, and the assembly code can be accessed at will. Any fast access, any address can be accessed, and the disk cannot be accessed
How is the disk accessed?
Every time you access the disk, the disk is equivalent to the fan. It rotates again and again and turns to a fixed position. The disk is composed of many faces. Then how can we get data from this face in the process?
It supports the disk through the magnetic head, then addresses it, finds the fixed track, and then gets the corresponding data. It may be a bit tongue twisty at first. It can be understood that this is equivalent to a bowl cabinet. The cabinet where you put the dishes and chopsticks in your home, a lot of plates, and some fixed data is stored in the middle of the plate. Where is the slow speed of the disk? In the middle of this addressing process, addressing is very slow. It turns to the fixed position and gets the determined data. It is very slow. Hold the disk head, find the corresponding sector of the disk and get the data
When working as an operating system, you will specify the sector. This place is where the boot is stored. When the operating system starts, it just starts to start from this sector, gets the data, and then executes the instructions in the middle of starting to load the memory. This is not the focus of today's article. The focus is that the disk is slow and slow is addressing
What's the difference between this slow and this memory access?
Then you can refer to my last article on red and black trees. What is red and black trees like? It can be understood as a binary tree. Take an example of a binary tree. 1024 nodes. Imagine what 1024 nodes mean. There are 10 layers high. How do you find the 10 layers?
Get the root node first, through one-time addressing? What do you mean? This pointer points to the next position, which is an addressing; In the worst case, 1024 nodes need to be addressed 10 times to get the data we want. Please note that this method is no problem For the same red black tree, when we take it to the disk to run, we will find a problem. It doesn't mean we can't do it. Let's combine this situation. We put it in the disk and also need addressing. For the same 1024 nodes, we need to address the disk 10 times. What's the meaning of taking this 10 times of disk addressing? It is equivalent to the disk turning on the track ten times, that is, we need to find it ten times. Please note that this ten times is still in the process of finding. We need to address a data 10 times and write a data 10 times. You will find that the speed of accessing the disk will be greatly reduced
Is there a way to reduce the addressing times, that is, reduce the tree layer height. The less the addressing times, the better. The faster one or two times, the better
Under this prospect, there is our multi fork tree. The multi fork tree is designed to be under the same node. For example, six forks and eight forks can be addressed twice. This multi fork tree is to reduce the layer height and the addressing speed. Then there is a tree called B tree in the middle of the multi fork tree, and there are many kinds of trees in the middle of the multi fork tree,
What kind of 3-ary tree, 4-ary tree, 5,btree is also a multi ary tree. When defining it, there is no fork tree defined?
According to the number of child nodes you have, the number of forks is defined by the application program, which is written by ourselves. It has more variability than trigeminal tree, 4-fork tree and even N-fork tree. When we talk about this multi fork tree, we are often equivalent to talking about the B tree. There are not many forks defined on the definition of B tree,
First, explain why the B tree is often used. After explaining the B tree, explain the B + tree,
According to such a situation, for example, when each node addresses the operation memory in 4k pages, the minimum unit is 4k,
How many addressing times do we need for 4Gd storage
The B tree has 1024 forks. It only needs to be addressed twice,
How to define a B-tree?
All leaf nodes are on the same layer, which determines the balance
I believe many friends are explaining such a problem? How did this definition come from
I want to ask whether there is a B-tree or a definition first?
First, we have the definition of the tree, and slowly go to the version iteration to restrict what we do

Is there a result first?
Logical contradiction: think about the definition and then think about the tree,
First understand the tree and then think about the definition. A convention is OK
26 letter B-tree
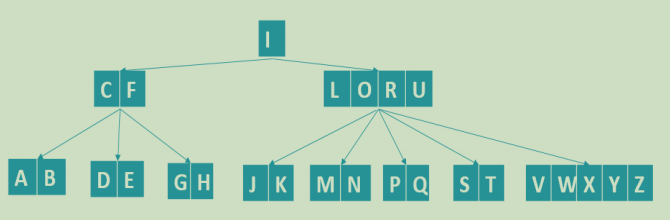
The root node has at least two subtrees. This is true. The second one is that all leaf nodes are on the same layer,
And this concept will be explained to you
The largest tree in this order, that is, how many letters can be stored in this node?
5, the largest 5, is equal to the M-order 5 + 1 defined by us. How many key s does this 5 describe
If the key is 5 at most, there are 6 subtrees. The M-order represents the maximum number of nodes in the subtree. There are 6 gaps in the queue of 5 people
Be able to see the B-tree in combination with the code;
The organization of the same letter B tree is N diverse
How is the B-tree defined in code?
First define a node. How many K and subtrees does this node contain, and then include other information, such as how to define order M? How many K values are there? Is it a leaf node?


A sector is a node, and the sector can be found by addressing several times;
The flexible array is used in the memory. The memory has been allocated. When we don't need to know its size, we can access it directly through a label,
So how can we change a B-tree from a node to n multiple nodes?
How many units are there in total?
How to organize a million quick
Is there only a definite way for 26 letters?
Split before adding

M selects even k odd
Talk about splitting before creating
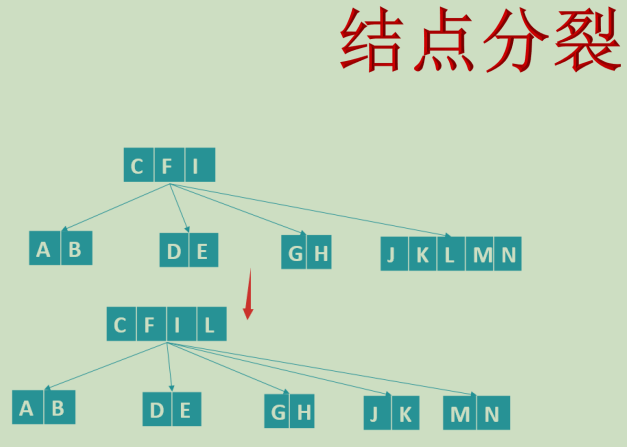
If there is only one node, how can it split? The ith child node cannot split. How many children does it have,
After splitting, there are two steps to insert the node at the corresponding position:
Find the corresponding position and put the corresponding node in,
Like a binary sort tree, compare node k to find the right position
How? Plug in this node
Just look at a B-tree. The newly inserted k value of this node is finally inserted into the leaf node. It is impossible to insert the inner node,
All nodes are inserted into leaf nodes, so how do we implement our code?
For example, insert aa larger than u, and then split
Also introduce functions
This x is the incomplete node we want to insert. It doesn't mean,
It's not the function we inserted, it's a full node
x means that this process is recursive, that is, a is not a leaf node. Find one and insert it,
If (leaf node insertion, not leaf node recursion)
In contrast, the value of k is actually the position of its subtree, and the first one smaller than it is found
Its subtree is his closest position
If the subtree is found to be full, split it first
Find the appropriate position, and then judge whether the subtree is full. If it is full, split it first
Is full and then split
Three steps together
After splitting, continue to find whether the corresponding subtree is full. Insert it after splitting. Don't judge whether it is full after splitting
Insert a self. OK, OK, it will be full of split when inserting the node next time. It will not split when it is just full,
Deleting nodes is complicated
Find rules
When deleting, the first search is exactly equal to the minimum value, and the traversal is exactly equal to the lower limit. At this time, the borrow action appears,
Several steps have taken place:
1. When to borrow and when to delete
Such situations 4
1. Compare the two subtrees, idx-1 and INX + 1. If IDX is equal to the minimum quantity, a. There are two cases of borrow and borrow. When to borrow forward and when to borrow backward, judge the front and judge the back
B. Merge if idx
2. If the subtree is larger than, let it be, and merge if it can't be borrowed,
Why merge C,
When deleting, the first step is to recursively find the corresponding subtree
The process of finding a subtree is a recursive process,
The value of the deleted node will also be on the leaf node
Composition of B-tree

Implementation of B-tree
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
//The value of M/2 is convenient for directly judging merging and splitting later
#define DEGREE 3
typedef int KEY_VALUE;
typedef struct _btree_node {
KEY_VALUE *keys;//Array M-1
struct _btree_node **childrens;
int num;//Not full
int leaf;//In fact, it is a state. Why not bool? The situation is the same
} btree_node;
typedef struct _btree {
btree_node *root;
int t;
} btree;
btree_node *btree_create_node(int t, int leaf) {
btree_node *node = (btree_node*)calloc(1, sizeof(btree_node));
if (node == NULL) assert(0);
node->leaf = leaf;
node->keys = (KEY_VALUE*)calloc(1, (2*t-1)*sizeof(KEY_VALUE));
node->childrens = (btree_node**)calloc(1, (2*t) * sizeof(btree_node));
node->num = 0;
return node;
}
void btree_destroy_node(btree_node *node) {
assert(node);
free(node->childrens);
free(node->keys);
free(node);
}
void btree_create(btree *T, int t) {
T->t = t;
btree_node *x = btree_create_node(t, 1);
T->root = x;
}
//Pass that node, okay? 1 or 2, there is no parent node to go up, the ith split
void btree_split_child(btree *T, btree_node *x, int i) {
int t = T->t;
btree_node *y = x->childrens[i];
btree_node *z = btree_create_node(t, y->leaf);
z->num = t - 1;
int j = 0;
for (j = 0;j < t-1;j ++) {
z->keys[j] = y->keys[j+t];
}
if (y->leaf == 0) {
for (j = 0;j < t;j ++) {
z->childrens[j] = y->childrens[j+t];
}
}
y->num = t - 1;
for (j = x->num;j >= i+1;j --) {
x->childrens[j+1] = x->childrens[j];
}
x->childrens[i+1] = z;
for (j = x->num-1;j >= i;j --) {
x->keys[j+1] = x->keys[j];
}
x->keys[i] = y->keys[t-1];
x->num += 1;
}
void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) {
int i = x->num - 1;
if (x->leaf == 1) {
while (i >= 0 && x->keys[i] > k) {
x->keys[i+1] = x->keys[i];
i --;
}
x->keys[i+1] = k;
x->num += 1;
} else {
while (i >= 0 && x->keys[i] > k) i --;
if (x->childrens[i+1]->num == (2*(T->t))-1) {
btree_split_child(T, x, i+1);
if (k > x->keys[i+1]) i++;
}
btree_insert_nonfull(T, x->childrens[i+1], k);
}
}
void btree_insert(btree *T, KEY_VALUE key) {
//int t = T->t;
btree_node *r = T->root;
if (r->num == 2 * T->t - 1) {
btree_node *node = btree_create_node(T->t, 0);
T->root = node;
node->childrens[0] = r;
btree_split_child(T, node, 0);
int i = 0;
if (node->keys[0] < key) i++;
btree_insert_nonfull(T, node->childrens[i], key);
} else {
btree_insert_nonfull(T, r, key);
}
}
void btree_traverse(btree_node *x) {
int i = 0;
for (i = 0;i < x->num;i ++) {
if (x->leaf == 0)
btree_traverse(x->childrens[i]);
printf("%C ", x->keys[i]);
}
if (x->leaf == 0) btree_traverse(x->childrens[i]);
}
void btree_print(btree *T, btree_node *node, int layer)
{
btree_node* p = node;
int i;
if(p){
printf("\nlayer = %d keynum = %d is_leaf = %d\n", layer, p->num, p->leaf);
for(i = 0; i < node->num; i++)
printf("%c ", p->keys[i]);
printf("\n");
#if 0
printf("%p\n", p);
for(i = 0; i <= 2 * T->t; i++)
printf("%p ", p->childrens[i]);
printf("\n");
#endif
layer++;
for(i = 0; i <= p->num; i++)
if(p->childrens[i])
btree_print(T, p->childrens[i], layer);
}
else printf("the tree is empty\n");
}
int btree_bin_search(btree_node *node, int low, int high, KEY_VALUE key) {
int mid;
if (low > high || low < 0 || high < 0) {
return -1;
}
while (low <= high) {
mid = (low + high) / 2;
if (key > node->keys[mid]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return low;
}
//{child[idx], key[idx], child[idx+1]}
void btree_merge(btree *T, btree_node *node, int idx) {
btree_node *left = node->childrens[idx];
btree_node *right = node->childrens[idx+1];
int i = 0;
/data merge
left->keys[T->t-1] = node->keys[idx];
for (i = 0;i < T->t-1;i ++) {
left->keys[T->t+i] = right->keys[i];
}
if (!left->leaf) {
for (i = 0;i < T->t;i ++) {
left->childrens[T->t+i] = right->childrens[i];
}
}
left->num += T->t;
//destroy right
btree_destroy_node(right);
//node
for (i = idx+1;i < node->num;i ++) {
node->keys[i-1] = node->keys[i];
node->childrens[i] = node->childrens[i+1];
}
node->childrens[i+1] = NULL;
node->num -= 1;
if (node->num == 0) {
T->root = left;
btree_destroy_node(node);
}
}
void btree_delete_key(btree *T, btree_node *node, KEY_VALUE key) {
if (node == NULL) return ;
int idx = 0, i;
while (idx < node->num && key > node->keys[idx]) {
idx ++;
}
if (idx < node->num && key == node->keys[idx]) {
if (node->leaf) {
for (i = idx;i < node->num-1;i ++) {
node->keys[i] = node->keys[i+1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) { //root
free(node);
T->root = NULL;
}
return ;
} else if (node->childrens[idx]->num >= T->t) {
btree_node *left = node->childrens[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
} else if (node->childrens[idx+1]->num >= T->t) {
btree_node *right = node->childrens[idx+1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
} else {
btree_merge(T, node, idx);
btree_delete_key(T, node->childrens[idx], key);
}
} else {
btree_node *child = node->childrens[idx];
if (child == NULL) {
printf("Cannot del key = %d\n", key);
return ;
}
if (child->num == T->t - 1) {
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->childrens[idx-1];
if (idx + 1 <= node->num)
right = node->childrens[idx+1];
if ((left && left->num >= T->t) ||
(right && right->num >= T->t)) {
int richR = 0;
if (right) richR = 1;
if (left && right) richR = (right->num > left->num) ? 1 : 0;
if (right && right->num >= T->t && richR) { //borrow from next
child->keys[child->num] = node->keys[idx];
child->childrens[child->num+1] = right->childrens[0];
child->num ++;
node->keys[idx] = right->keys[0];
for (i = 0;i < right->num - 1;i ++) {
right->keys[i] = right->keys[i+1];
right->childrens[i] = right->childrens[i+1];
}
right->keys[right->num-1] = 0;
right->childrens[right->num-1] = right->childrens[right->num];
right->childrens[right->num] = NULL;
right->num --;
} else { //borrow from prev
for (i = child->num;i > 0;i --) {
child->keys[i] = child->keys[i-1];
child->childrens[i+1] = child->childrens[i];
}
child->childrens[1] = child->childrens[0];
child->childrens[0] = left->childrens[left->num];
child->keys[0] = node->keys[idx-1];
child->num ++;
node->keys[idx-1] = left->keys[left->num-1];
left->keys[left->num-1] = 0;
left->childrens[left->num] = NULL;
left->num --;
}
} else if ((!left || (left->num == T->t - 1))
&& (!right || (right->num == T->t - 1))) {
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx-1);
child = left;
} else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
btree_delete_key(T, child, key);
}
}
int btree_delete(btree *T, KEY_VALUE key) {
if (!T->root) return -1;
btree_delete_key(T, T->root, key);
return 0;
}
int main() {
btree T = {0};
btree_create(&T, 3);
srand(48);
int i = 0;
char key[26] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
for (i = 0;i < 26;i ++) {
//key[i] = rand() % 1000;
printf("%c ", key[i]);
btree_insert(&T, key[i]);
}
btree_print(&T, T.root, 0);
for (i = 0;i < 26;i ++) {
printf("\n---------------------------------\n");
btree_delete(&T, key[25-i]);
//btree_traverse(T.root);
btree_print(&T, T.root, 0);
}
}
