Backtracking algorithm
"It is common in the world that if you don't advance, you will retreat, if you don't like it, you will worry, and if you don't have it, you will die." --- Deng Xizi · Chapter II
preface
Backtracking method is known as the universal solution, and it also contains the life philosophy of taking a step back.
1, Backtracking and backtracking algorithm
(1) What is "backtracking"?
Lost beauty, you want to find the heart at that time in repetition, go back along the track, but all the passing scenery is not the meaning of that year. There are only two kinds of people left in the world: like her and unlike her.
(2) What is "backtracking algorithm"?
Backtracking method is a kind of optimization search method, which gives priority to depth search according to the optimization conditions until the goal is achieved. When a certain step is searched and it is found that the original selection is not optimal or the goal cannot be reached, it will go back to one step for re selection. This technology of going back and going again if it fails is called backtracking method, and a state that meets the backtracking conditions is called "backtracking point".
2, Example presentation - 0-1 knapsack problem
(1) Problem description
0-1 knapsack problem: provide a shopping cart with a capacity (also can be regarded as the load capacity) of W and n items. The value of each item i is Vi and the weight is Wi. There is only one item for each item, which can be loaded or not loaded. It is inseparable. How to select items to maximize the value of loading into the shopping cart.
(2) Problem analysis
Selecting some items from n items is equivalent to finding a subset from the set S composed of n items. The total weight of all items in the subset shall not exceed the capacity of the shopping cart, and the total value of these items is the largest when the conditions are met.
(3) Algorithm design
1. Define the solution space of the problem
For each item, there are only two results, load and no load, but whether the item is loaded or not is unknown. Therefore, for convenience, the variable Xi can be defined to indicate whether the ith item is loaded. If it is loaded, the value of Xi is 1, otherwise it is 0. The solution of the problem is an n-tuple, and the value of each component is 0 or 1, The solution space of the problem is {X1, X2, X3, ·······, Xn}, where Xi is 0 or 1 and i is 1, 2, 3, 4, ·······, n.
2. Determine the organizational structure of the solution space
It is not difficult to see that the solution of the problem is the number of all subsets of a set composed of n elements.
For example, if the value of n is 3 (i.e. there are 3 items in total), the solution space is {0, 0, 0}, {0, 0, 1}, {0, 1, 1}, {1, 1, 1}, {0, 1, 0}, {1, 0, 1}, {1, 1, 0}.
It can be seen that the depth of the solution space tree of the problem is the scale n of the problem (that is, the total number of items).
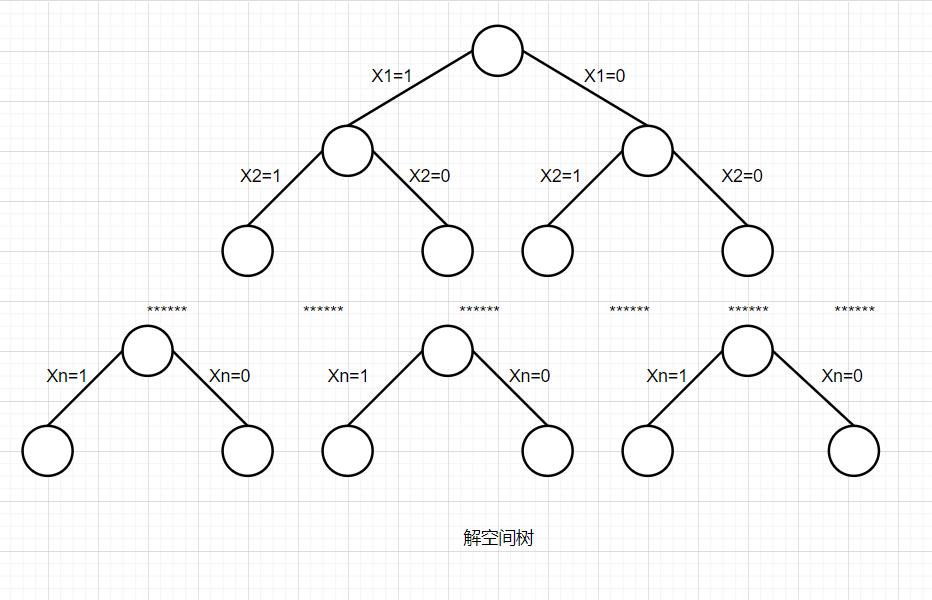
3. Search solution space
Constraints:
It is easy to see that Σ wi Xi < = w (the lower bound is i=1 and the upper bound is n)
scope condition
According to the organizational structure of the solution space, for any intermediate node z, the state represented by the branch from the root node to the z node (whether to load the shopping cart or not) It has been determined that the branch state from z to its descendant node is uncertain, that is, if z is in the t-th layer in the solution space tree, it indicates that the state of the first article to the t-1 article has been determined, and we only need to expand along the branch of z to determine the state of the t-th article. For convenience, we use CP to represent the total value of the articles loaded into the shopping cart. Remember, The high value loaded is not necessarily optimal because there are other situations that are not determined.
Since we have not determined the actual situation of items t+1 to N, we can only estimate their situation. Suppose that items t+1 to n are loaded into the shopping cart, and the total value of items t+1 to n is expressed by rp, so CP+rp is the upper bound of the value of all feasible solutions starting from the root and passing through the intermediate node z.
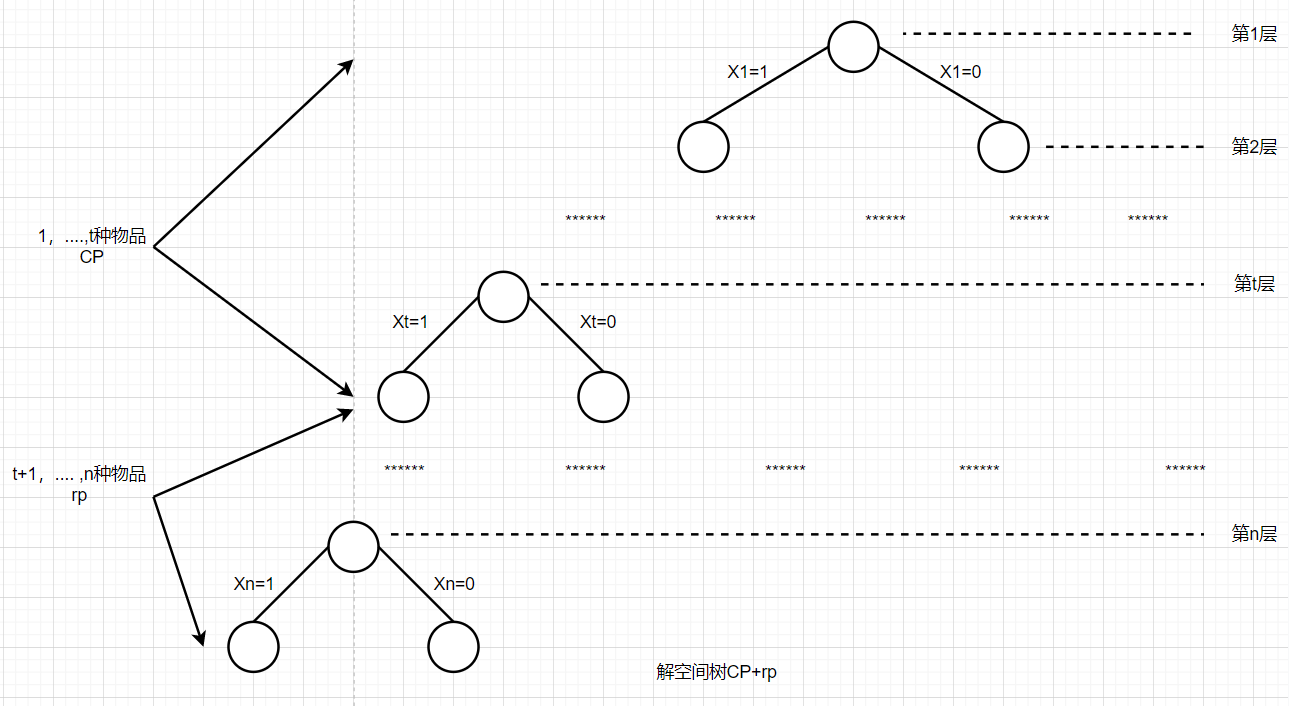
If the upper bound of value is less than or equal to the currently searched optimal value (the optimal value is represented by bestp and the initial value is 0), there is no need to continue the search. On the contrary, continue the search.
Clearance condition: CP + RP > bestp
search process
Starting from the root node, the depth first search. The root node first becomes the live node and the current expansion node. The left branch is defined as 1, that is, the left subtree indicates that the item is placed in the shopping cart, and the right branch is 0, indicating that it is not placed in the shopping cart. Start to expand along the left branch, and then you need to judge whether the limiting conditions are met. If so, continue to expand along the left branch, No Then expand along the right branch. If not, go back to the nearest parent node and continue to expand other cases until all cases are considered.
(4) Simulation process
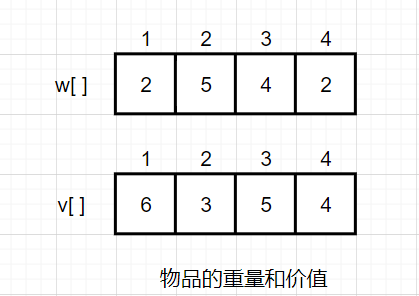
Suppose there are four items and a shopping cart. The weight W of each item is (2, 5, 4, 2), the value is (6, 3, 5, 4), and the weight W of the shopping cart is 10
1. Initialization
Sumw and sumv are used to count the total weight and total value of all items respectively. sumw=13, sumv=18, sumw > W, so they cannot be completely loaded and need to be selected. The current weight put into the shopping cart is cw=0, the current value put into the shopping cart is cp=0, and the current optimal value is bestp=0
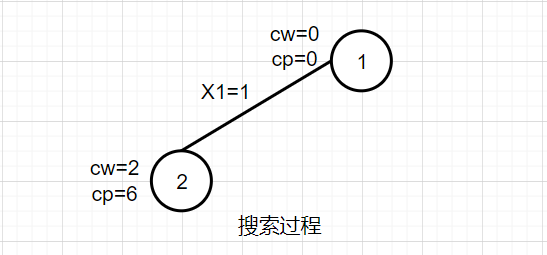
2. Search the first layer
To expand node 1, first judge that CW + w [1] = 2 < w meets the constraints, expand the left branch, make X[1]=1,cw=cw+w[1]=2,cp=cp+v[1]=6, and generate node 2.
3. Extend node 2
First, judge that CW + w [2] = 7 < W, meet the constraints, expand the left branch, make x[2]=1,cw=cw+w[2]=7,cp=cp+v[2]=9, and generate node 3.
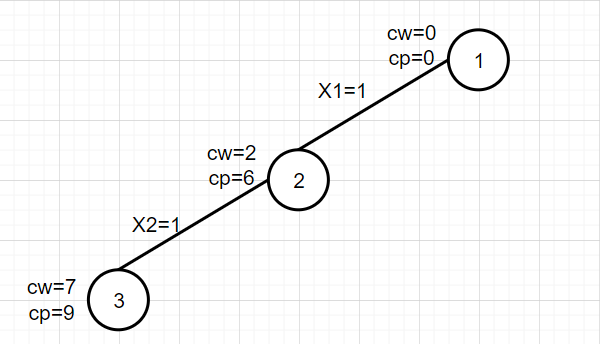
4. Extend node 3
First, judge that CW + w [3] = 11 > W exceeds the capacity of the shopping cart and the third item cannot be put in. Then judge whether the bound(t+1) is greater than bestp. There are only the fourth item in bound (4), rp=4,cp+rp=13,bestp=0. Therefore, meet the limit conditions and expand the right subtree. Let x[3]=0 to generate node 4.
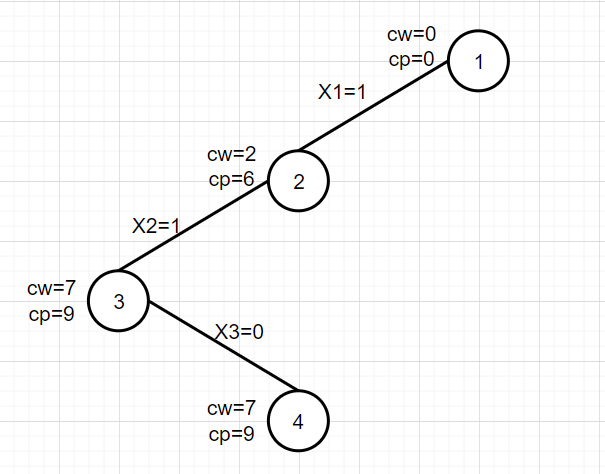
5. Expand node 4
First, judge that CW + w [4] = 9 < W, meet the constraints, expand the left branch, make x[4]=1,cw=cw+w[4]=9,cp=cp+v[4]=13, and generate node 5.
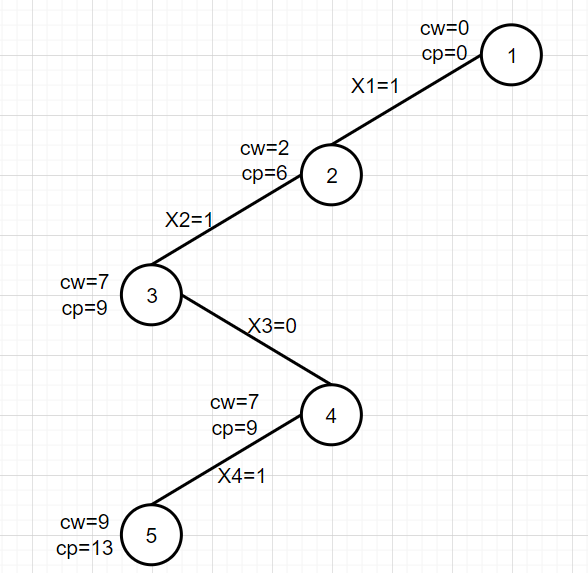
6. Expand node 5
t> N, find the current optimal solution, save the current optimal solution {1, 1, 0, 1} with bestx [], save the current optimal value bestp=13, and node 5 becomes the dead point.
7. Trace back to node 4 and up to node 2.
Backtrack up to node 4. When backtracking, cw=cw-w[4]=7,cp=cp-v[4]=9. How to add and how to subtract. The right subtree of node 4 has not been generated. Check bound (t+1) If it is greater than bestp, it can be judged that it does not meet the conditions, so it is not expanding the right branch of node 4, and node 4 is the dead point. Continue to backtrack to node 3, which has been investigated by children around node 3 and is the dead point. Continue to backtrack to node 2, cw=cw-w[2]=2,cp=cp-v[2]=6
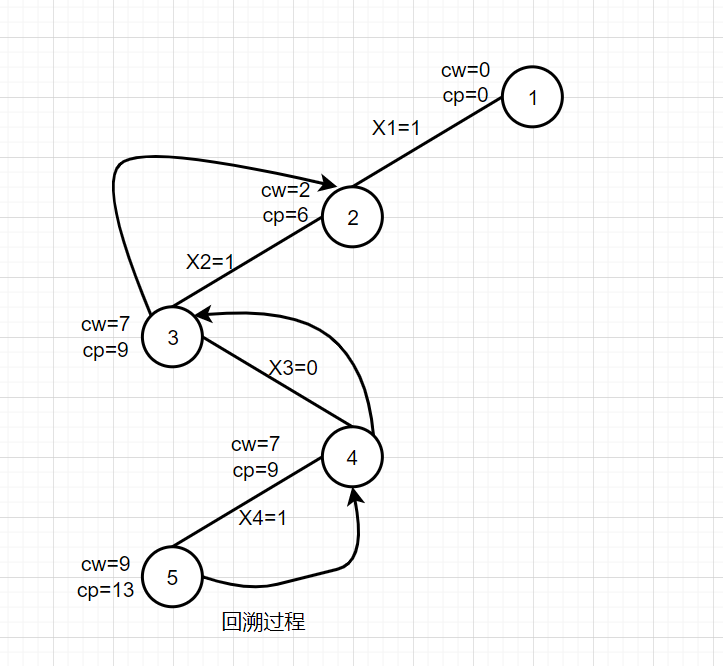
8. Extend node 2
The right subtree of node 2 has not been generated. Check whether the bound(t+1) is greater than bestp. The remaining items in bound (3) are the third and fourth items, RP = 9, CP + RP = 15 > bestp = 13. If the conditions are met, expand the right subtree. Let x[2]=0 to generate node 6.
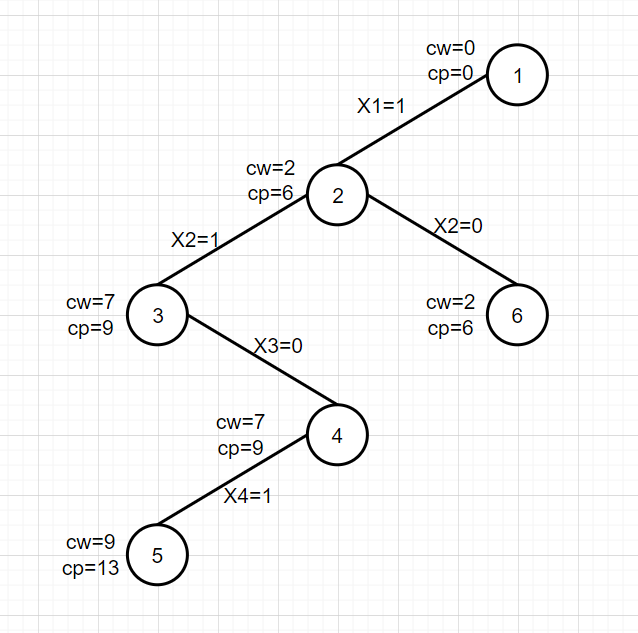
9. Expand node 6
First, judge that CW + w [3] = 6 < W, meet the constraints, expand the left branch, make x[3]=1,cw=cw+w[3]=6,cp=cp+v[3]=11, and generate node 7.
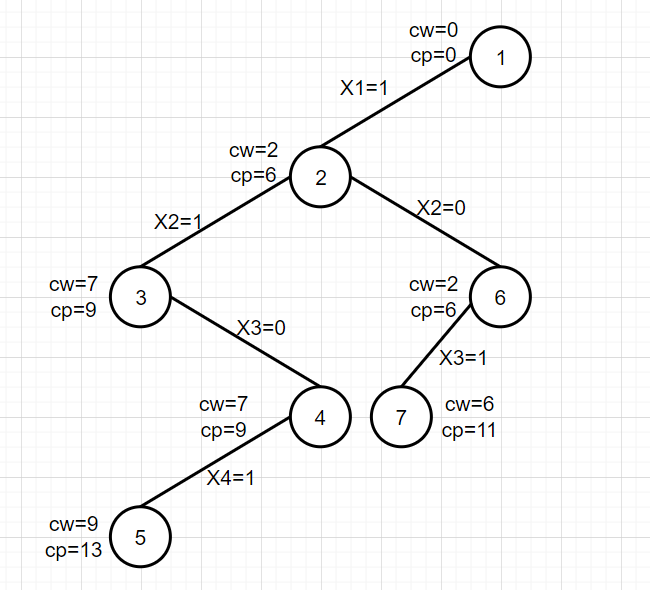
10. Expand node 7
First, judge that CW + w [4] = 8 < W, meet the constraints, expand the left branch, make x[4]=1,cw=cw+w[4]=8,cp=cp+v[4]=15, and generate node 8.
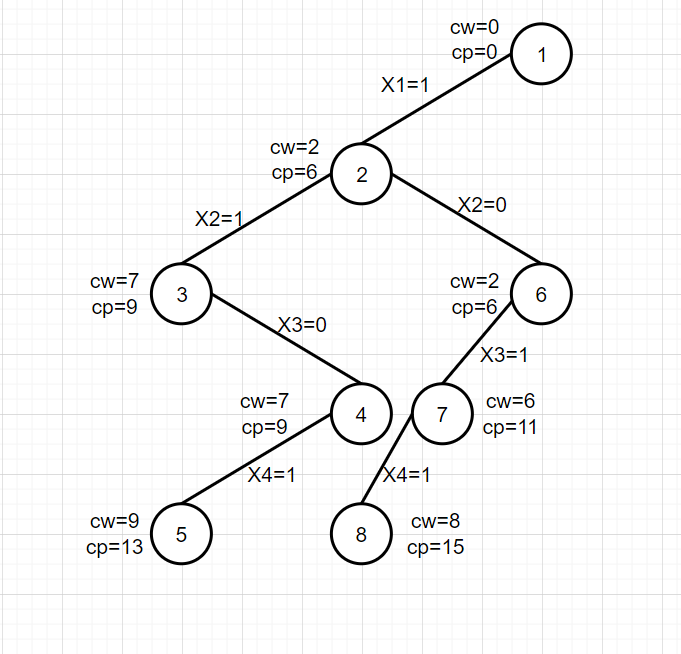
11. Expand node 8
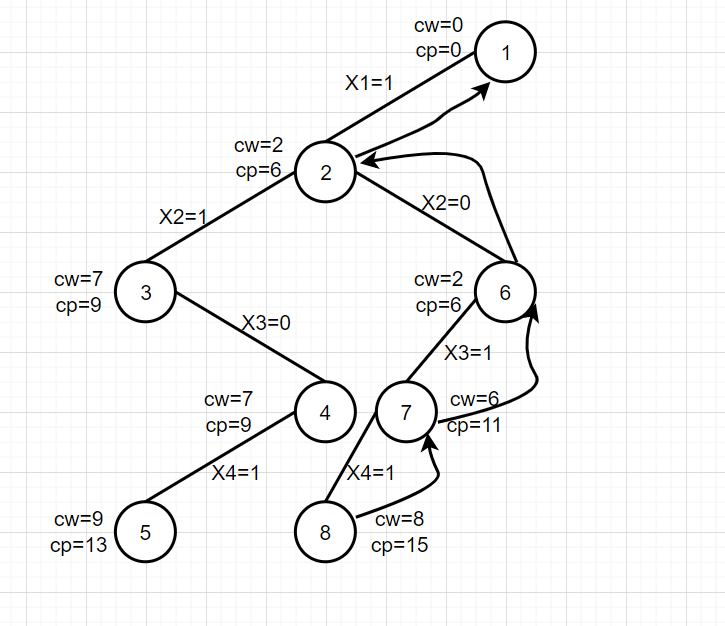
t> N, find an optimal solution, save the optimal solution {1, 0, 1, 1} with bestx [], save the optimal value bestp = 10, No. 8 as the dead point, and trace back to node 7, cw=cw-w[4]=6,cp=cp-v[4]=11
12. Expand node 7
The right subtree No. 7 has not been generated. It is found that it does not meet the boundary conditions and will not be extended. It is traced back to node No. 6, cw=cw-w[3]=2,cp=cp-v[3]=6
13. Expand node 6
The right subtree of node 6 is not generated. It is judged that it does not meet the limit conditions. Go back to node 2, cw=cw-w[1]=0,cp=cp-v[1]=0
14. Expand node 1
The right branch of node 1 is not generated. It is judged that it does not meet the limit conditions, and the algorithm ends.
(4) Code implementation
C + + code
double Bound(int i) //Computational upper bound
{
int rp=0; //The remaining items are items i to n.
while(i<=n) //Calculate the value of the remaining items in turn
{
rp+=v[i];
i++;
}
return cp+rp; //Return to upper bound
}
void Backtrack(int t) //T indicates that the current extension node is at layer t
{
if(t>n)
{
for(j=1;j<=n;j++)
{
bestx[j]=x[j];
}
bestrp=cp;
return ;
}
if(cw+w[t]<=W)
{
x[t]=1;
cw+=w[t];
cp+=v[t];
Backtrack(t+1);
cw-=w[t];
cp-=v[t];
}
if(Bound(t+1)>bestp)
{
x[t]=0;
Backtrack(t+1);
}
}
Python code
def backtrack(i):#global allows functions to handle variables outside of functions
global bestV, curW, curV, x, bestx
if i >= n:
if bestV < curV:
bestV = curV
bestx = x[:]
else:
if curW + w[i] <= c:
x[i] = True
curW += w[i]
curV += v[i]
backtrack(i + 1)
curW -= w[i]
curV -= v[i]
x[i] = False
backtrack(i + 1)
if __name__ == '__main__':
n = 5
c = 10
w = [2, 2, 6, 5, 4]
v = [6, 3, 5, 4, 6]
x = [False for i in range(n)]
backtrack(0)
print(bestV)
print(bestx)
Java code: quoted from CSDN blogger: snow invasion, article link: Snow invasion
/**
* to flash back
* @param t
*/
public static void BackTrack(int t) {
if(t>count) {//Reach leaf node
if(cp>bestp) {
for(int i = 1;i<=count;i++) {
bestx[i] = cx[i];
}
bestp = cp;
}
return;
}
r -= p[t];
if(cw + w[t] <= c) {//Search left subtree
cx[t] = 1;
cp += p[t];
cw += w[t];
BackTrack(t+1);
cp -= p[t];//Restore site
cw -= w[t];//Restore site
}
if(cp + r >bestp) {//Pruning operation
cx[t] = 0;//Search right subtree
BackTrack(t+1);
}
r += p[t];//Restore site
}
C language: transferred from CSDN blogger: Forever 9, article address: Forever 9
#include<stdio.h>
#define max 100
int weight[max];
int value[max];
int n,max_weight,max_value;
int best_answer[max],answer[max];
void print()
{
int i,j,k,l;
printf("+++++++++++++%d++++++++++++\n",max_value);
for(i=1;i<=n;i++)
printf("%d ",best_answer[i]);
printf("\n");
}
void DFS(int level,int current_weight,int current_value)
{
if(level>=n+1)
{
if(current_value>max_value)
{
int i;
max_value = current_value;
for(i=1;i<=n;i++)
best_answer[i] = answer[i];
}
}
else
{
if(current_weight>=weight[level+1])
{
current_weight = current_weight - weight[level+1];
current_value = current_value + value[level+1];
answer[level+1] = 1;
DFS(level+1,current_weight,current_value);
answer[level+1] = 0;
current_weight = current_weight + weight[level+1];
current_value = current_value - value[level+1];
}
DFS(level+1,current_weight,current_value);
}
}
void init()
{
int i,j,k,l;
max_value = 0;
for(i=1;i<=n;i++)
answer[i] = 0;
}
int main()
{
int i,j,k,l;
while(scanf("%d%d",&n,&max_weight)!=EOF)
{
for(i=1;i<=n;i++)
scanf("%d",&weight[i]);
for(j=1;j<=n;j++)
scanf("%d",&value[j]);
init();
DFS(0,max_weight,0);
print();
}
return 0;
}
summary
The essence of backtracking algorithm is a violent algorithm. After all, in the face of absolute strength, all fancy things are like ants. I have little talent and learning, and mistakes are inevitable. I hope you will give me advice and make more corrections. I thank you first. Finally, let me give you a word: the wind can blow out the candles, but it can make the fire burn more and more prosperous!
thank
Thanks to CSDN blog experts, top 5 blog stars in 2020 and signing author 1 of Blue Bridge Cup_ Bit's suggestions on my Python and algorithm learning;
Thank Professor Chen Xiaoyu of Nanyang Institute of technology for his network remote guidance;
Thanks to Liu Jingliang, senior student of didi travel, for his guidance of C + + and the sharing of valuable suggestions and resources on data structure and algorithm;
Thank you to Mr. Zhiyi Wang Jun for debugging, suggestions and help for my Python algorithm implementation;
Thank you for your suggestions and resource sharing.