4031: Swiss wheel
Total time limit: 2000ms single test point time limit: 1000ms memory limit: 65535kB
describe
[background]
In the competitive competition of duel, such as table tennis, badminton and chess, the most common competition system is knockout and round robin. The former is characterized by a small number of games, each of which is tense and exciting, but with high contingency. The latter is characterized by being more public
Flat, less chance, but the competition process is often very lengthy.
The Swiss round system introduced in this topic is named after the chess game held in Switzerland in 1895. It can be seen as a compromise between knockout and round robin, which not only ensures the stability of the game, but also makes the schedule not too long.

[problem description]
2*N players numbered 1~2N will compete in R rounds. Before the start of each round and after all competitions, the players will be ranked from high to low according to the total score. The total score of a player is the initial score before the start of the first round plus the sum of the scores of all competitions he has participated in. If the total score is the same, the player with the smaller agreed number will be ranked first. The match arrangement of each round is related to the ranking before the start of the round: first and second, third and fourth,..., 2k-1 and 2K,..., 2N-1 and 2n. In each game, the winner gets 1 point and the loser gets 0 point. In other words, except for the first round, the arrangement of other rounds of competition cannot be determined in advance, but depends on the performance of players in previous competitions.
Given the initial score and strength value of each player, try to calculate the number of the player ranking Q after the R round of competition. We assume that players have different strength values, and the one with higher strength value can always win in each game.

input
The first line of input is three positive integers N, R and Q, separated by a space between each two numbers, indicating that there are 2N players, R rounds of competition, and the ranking Q we care about.
The second line is 2N non negative integers s1, s2,..., s2N, separated by a space between each two numbers, where si represents the initial score of the player numbered i.
The third line is 2*N positive integers w1, w2,..., w2N, separated by a space between each two numbers, where wi represents the strength value of the player numbered i.
output
The output has only one line and contains an integer, that is, the number of the player ranking Q after the end of round R.
sample input
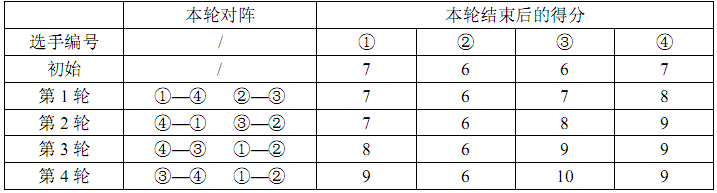
2 4 2
7 6 6 7
10 5 20 15
sample output
1
Tips
For 30% data, 1 ≤ N ≤ 100;
For 50% data, 1 ≤ N ≤ 10000;
For 100% data, 1 ≤ N ≤ 100000, 1 ≤ R ≤ 50, 1 ≤ Q ≤ 2N, 0 ≤ s1, s2,..., s2N ≤ 108, 1 ≤ w1, w2,..., w2N ≤ 108.

Question link: Bailian4031 Swiss wheel
Problem Description: (omitted)
Problem analysis: the score calculation of the competition system is not explained.
Program description: the original problem-solving program comes from TYUT.
Reference link: (omitted)
Caption: (omitted)

The C + + language program of AC is as follows:

/* Bailian4031 Swiss wheel */

#include <bits/stdc++.h>

using namespace std;

const int N = 2 * 1e5 + 2;
int s[N], w[N], num[N], win[N], lose[N];

bool cmp(int a, int b)
{
    return s[a] == s[b] ? a < b : s[a] > s[b];
}

void merge()
{
    int i = 1, j = 1;
    num[0] = 0;
    while (i <= win[0] && j <= lose[0]) {
        if (cmp(win[i], lose[j])) num[++num[0]] = win[i++];
        else num[++num[0]] = lose[j++];
    }
    while (i <= win[0]) num[++num[0]] = win[i++];
    while (j <= lose[0]) num[++num[0]] = lose[j++];
}

int main()
{
    int n, r, q;
    cin >> n >> r >> q;
    n *= 2;

    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        num[i] = i;
    }
    for (int i = 1; i <= n; i++) cin >> w[i];

    sort(num + 1, num + 1 + n, cmp);

    for (int i = 1; i <= r; i++) {
        win[0] = lose[0] = 0;
        for (int j = 1; j <= n; j += 2)
            if (w[num[j]] > w[num[j + 1]]) {
                s[num[j]]++;
                win[++win[0]] = num[j];
                lose[++lose[0]] = num[j + 1];
            } else {
                s[num[j + 1]]++;
                win[++win[0]] = num[j + 1];
                lose[++lose[0]] = num[j];
            }
        merge();
    }

    cout << num[q] << endl;

    return 0;
}