balanced binary tree

Balanced Binary Tree is also known as AVL tree.
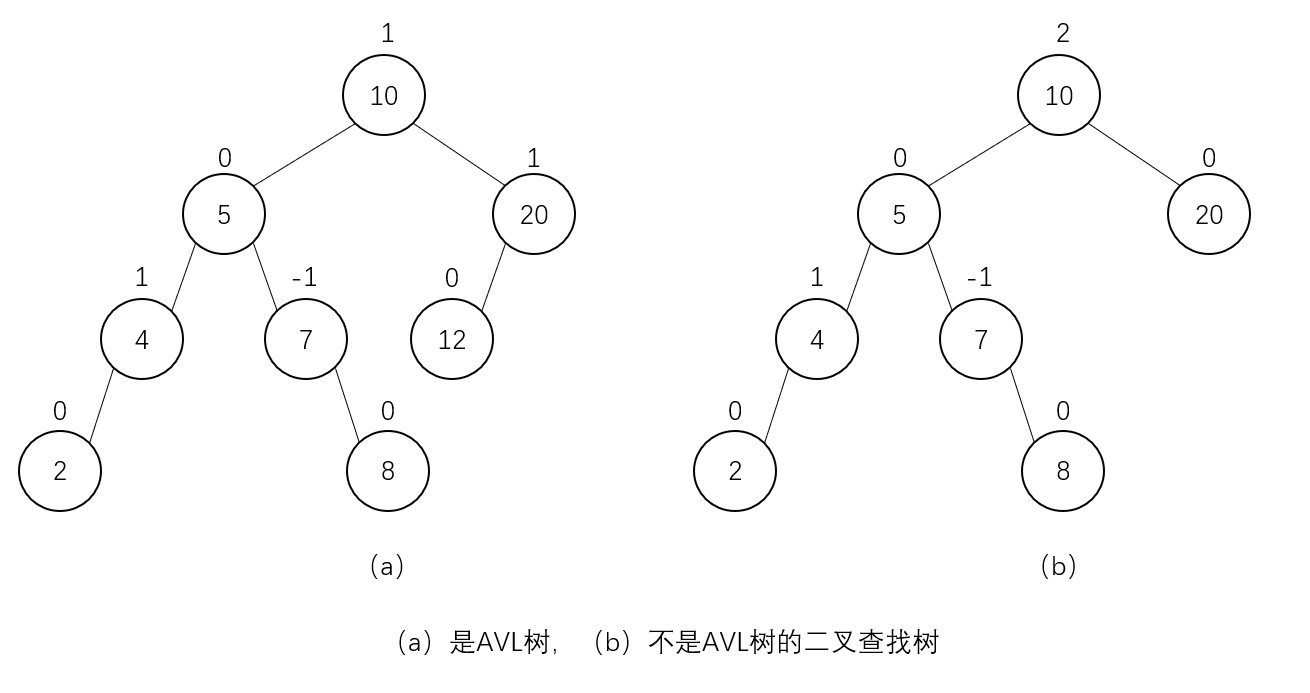
_Definition: An AVL tree is a binary lookup tree in which the balance factor for each node (defined as the height difference between the left and right subtrees of the node) is either zero or +1 or -1 (the height of an empty tree is defined as -1, although the balance factor can also be defined as the difference between the leaves of the left and right subtrees, not the height difference).

 
 

Rotation of AVL Tree

_If inserting a new node unbalances an AVL tree, we can use rotation to transform it. The rotation of an AVL tree is a local transformation of a subtree rooted on a node whose balance either becomes + 2 or -2. If there are several such nodes, we first find the unbalanced node closest to the newly inserted leaf, and then rotate the subtree rooted on that node. There are only four types of rotation, two of which are actually mirrors of the other two.

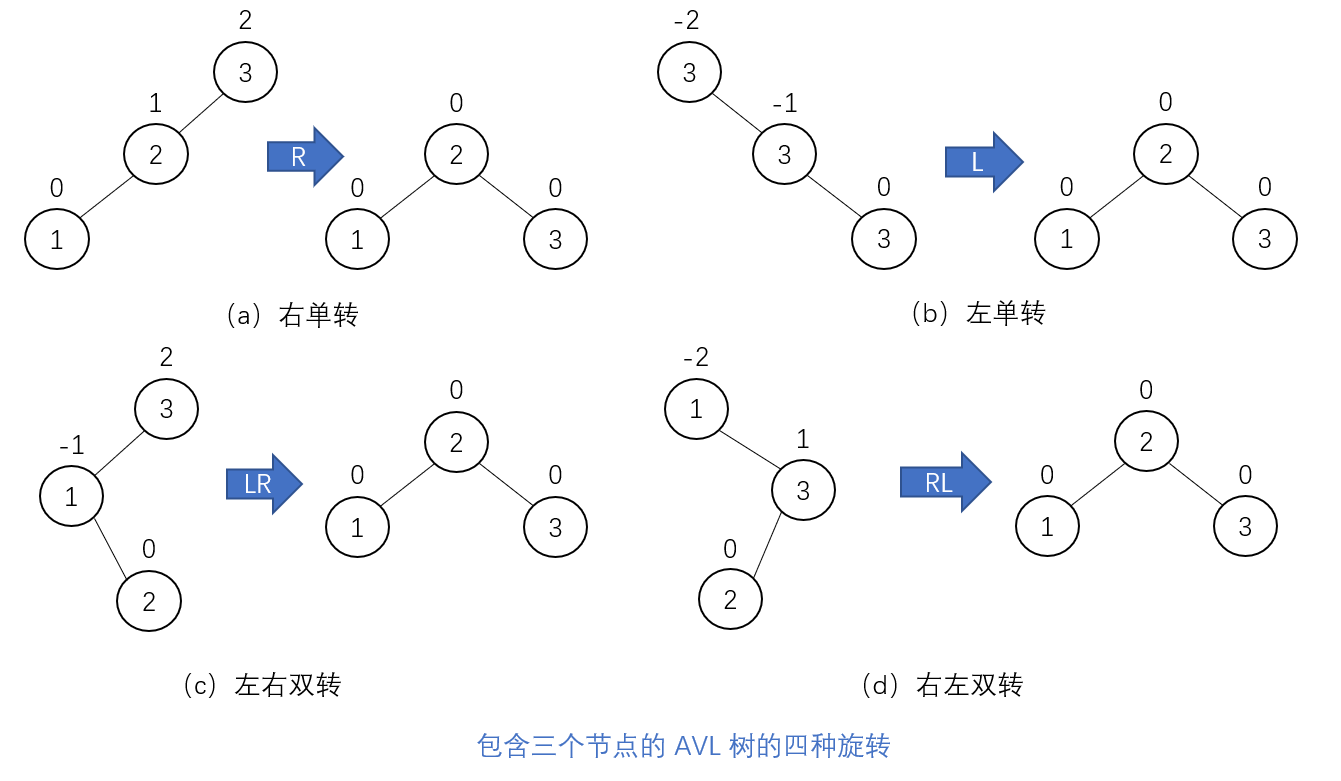
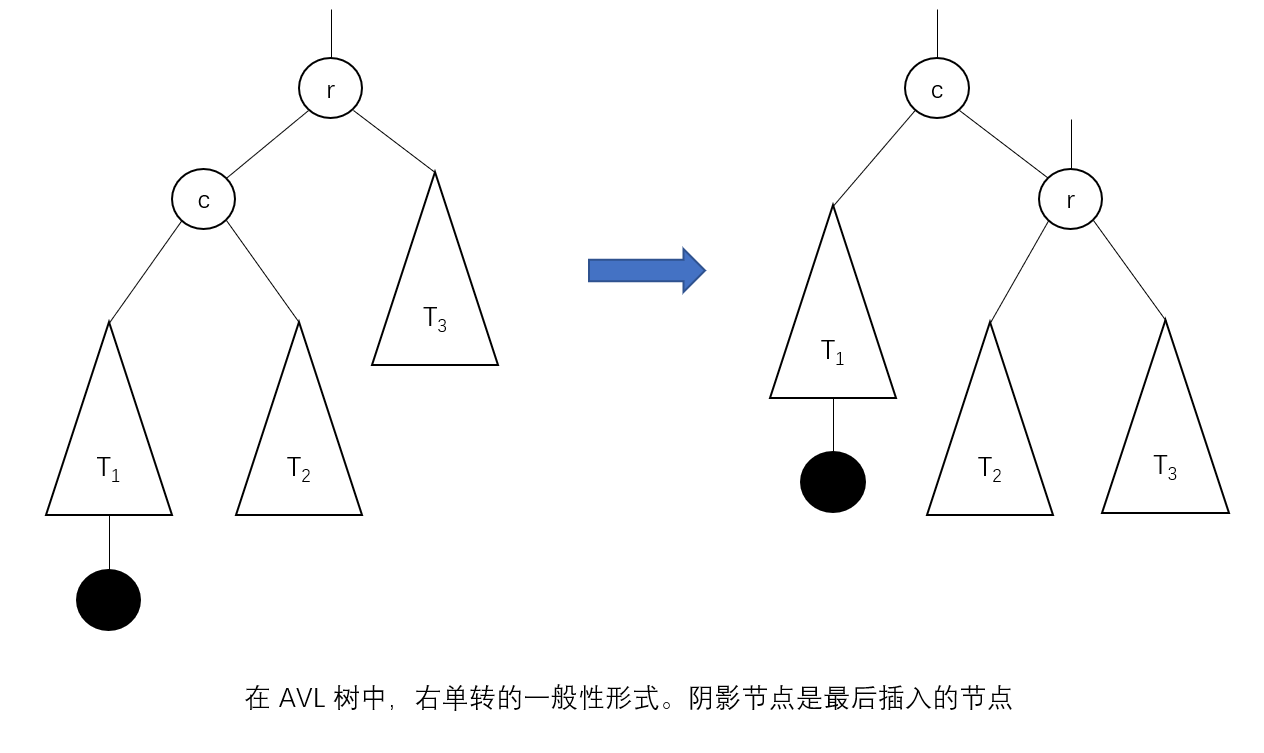
The first type of rotation is called a right one-way rotation or a right one-way rotation. The figure below is the most general form of a right turn.

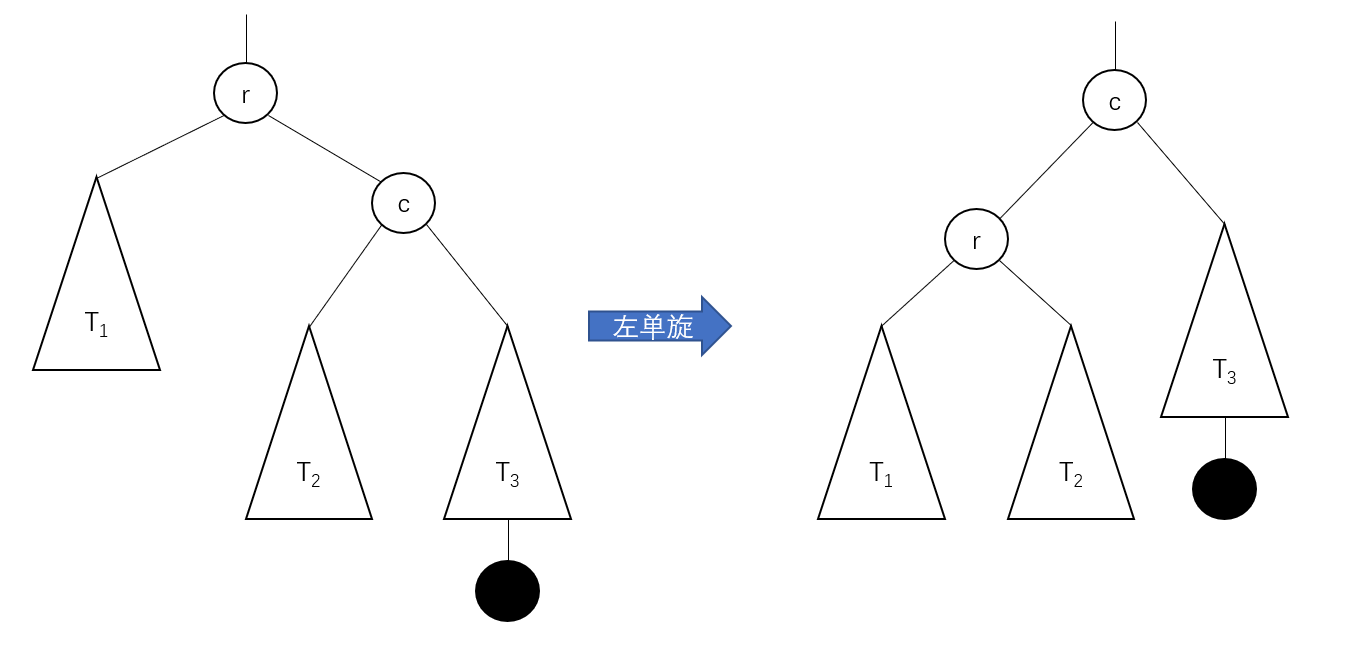
_corresponds to a left or left single turn, which is a mirror of a right single turn.
  
The second type of rotation is called two-way left-right rotation or left-right double rotation. In fact, it's a combination of two rotations: we rotate the left subtree of root R and rotate the new tree with root r to the right. Rotation occurs after a new key is inserted into the right subtree of the left child of the tree. The root balance factor for this tree is + 1 before insertion.

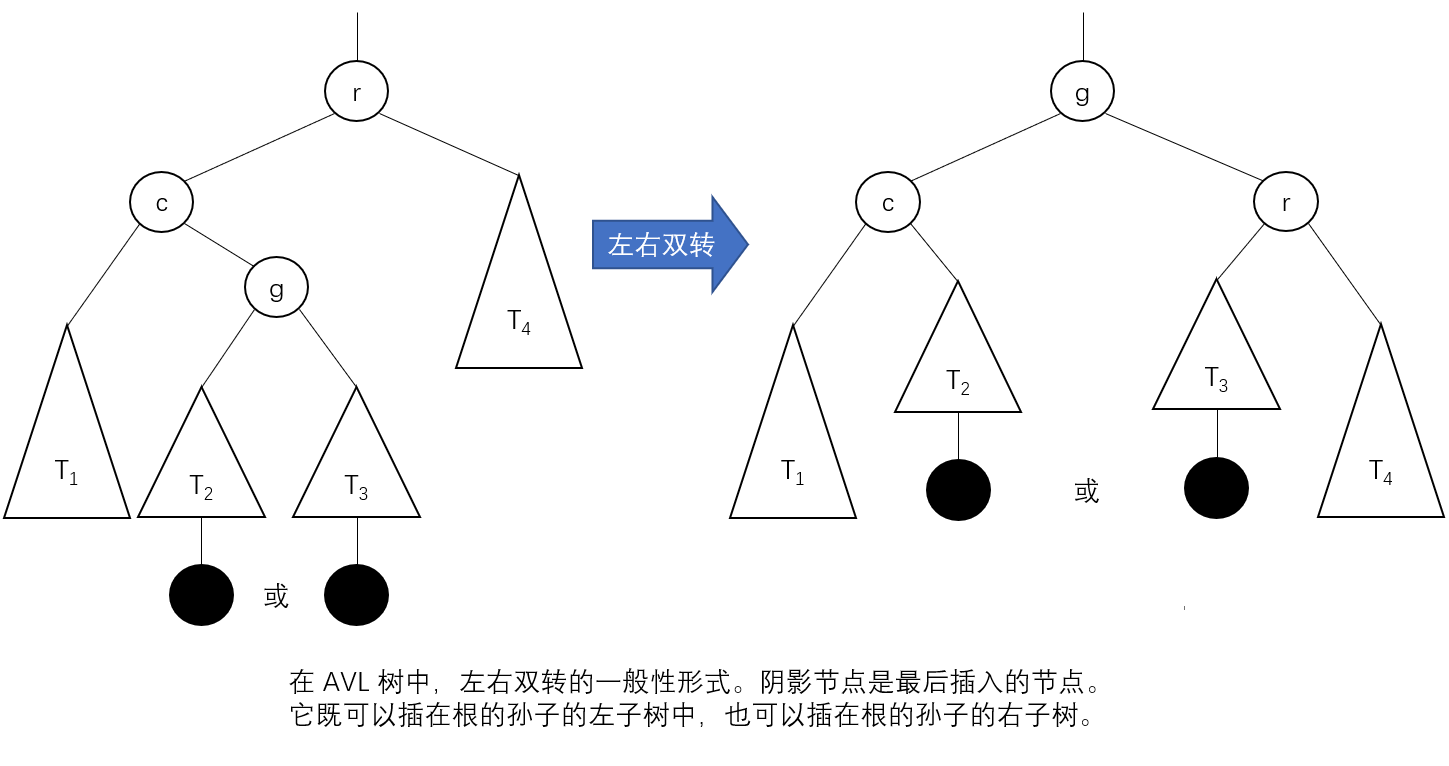
_Bidirectional right-left rotation, also known as right-left double rotation, is a mirror of left-right double rotation.
  
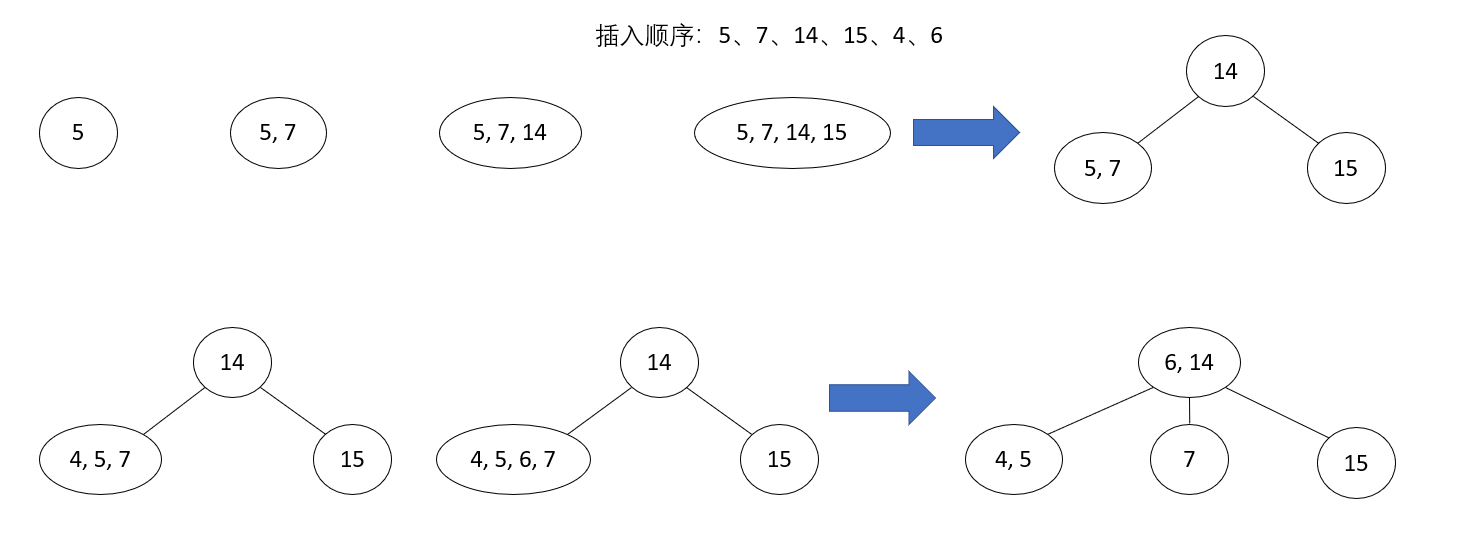
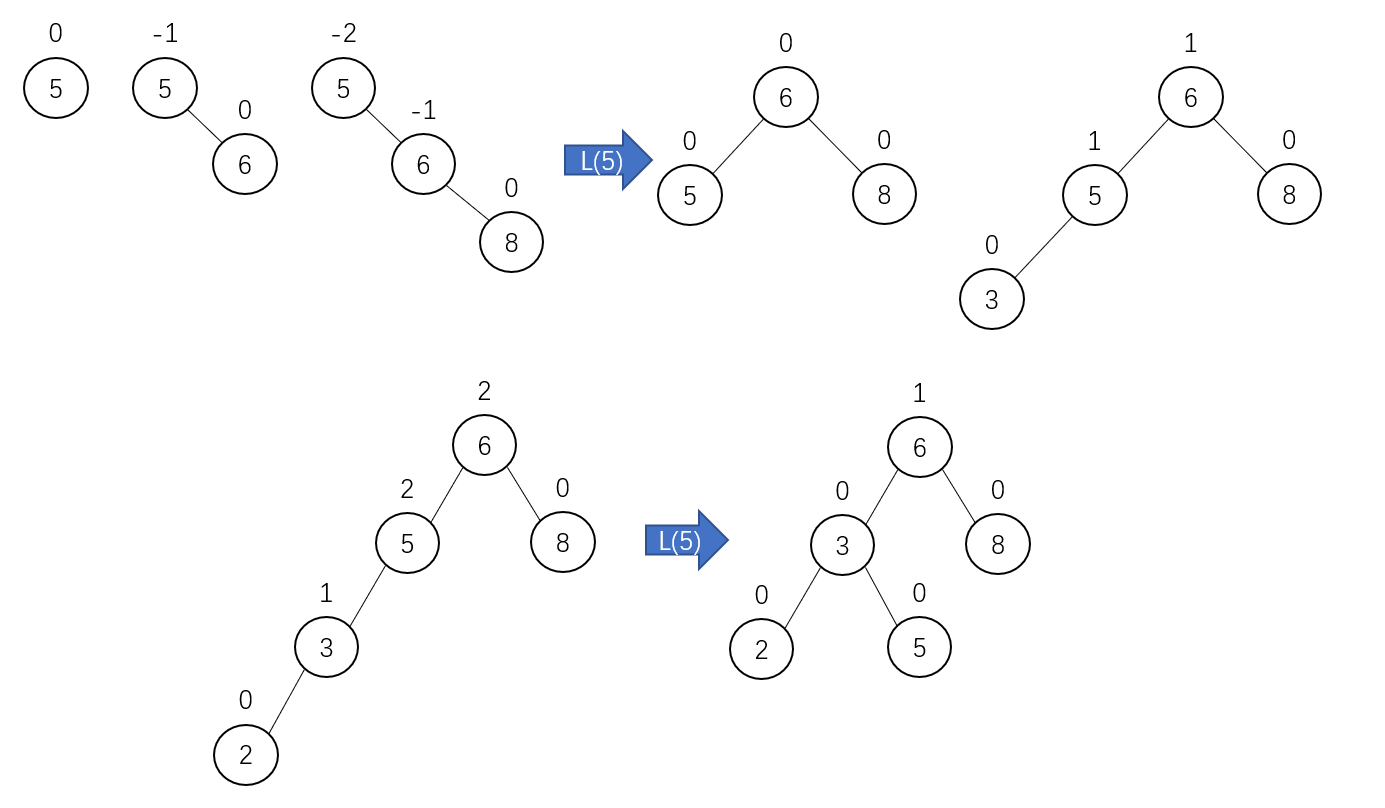
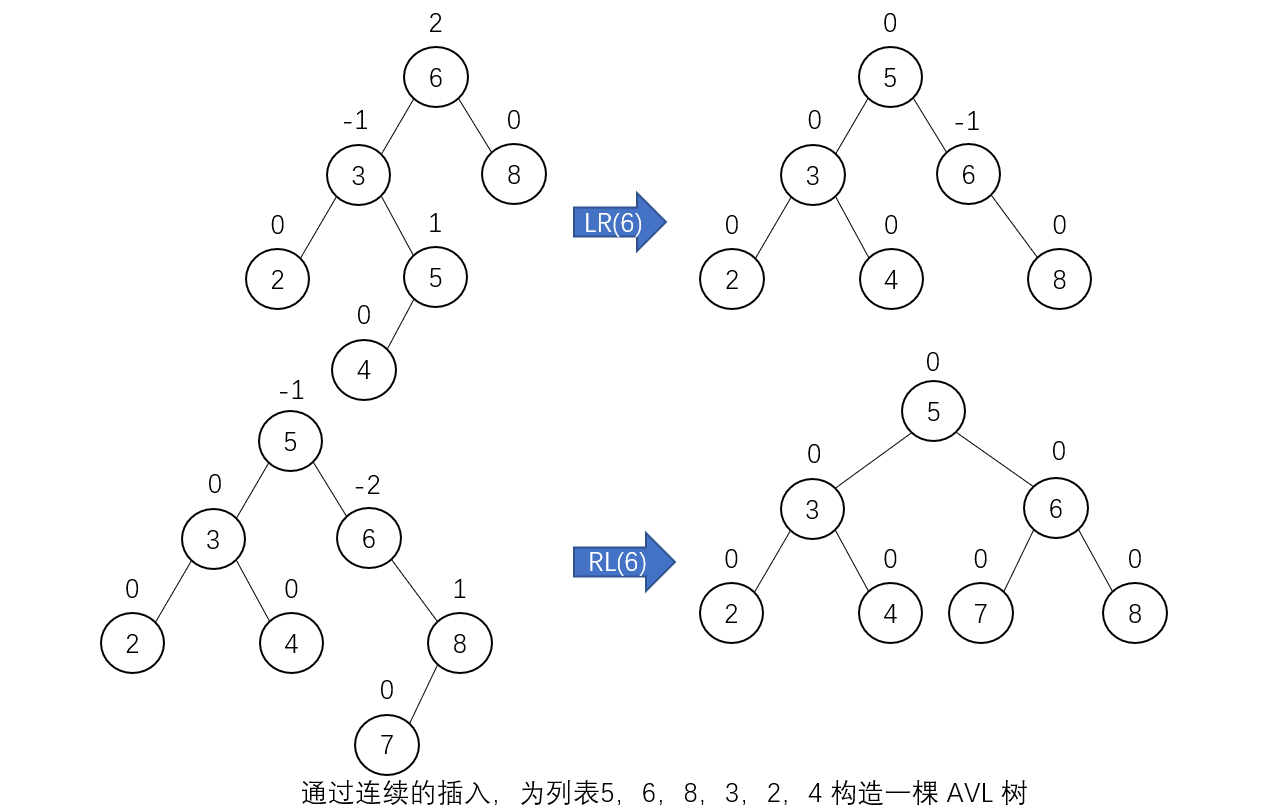
_Constructs an AVL tree for lists 5, 6, 8, 3, 2, 4, 7 through continuous insertions. The number in parentheses next to the rotated abbreviation indicates the root of the reorganized tree. Here's how to build an AVL tree:


 
 
 
 

code implementation

Define the balanced binary tree node structure:

typedef struct Node
{
    int key;//Node Data
    struct Node *left;//left child
    struct Node *right;//Right Child
    int bf;//Balance factor
}BTNode, *BiTree;

 
 

Right Single Turn (R)

BiTree R_Revolve(BiTree p){//Right Single Rotation on Binary Sort Tree Rooted with p
	BiTree l;
	l = p->left;
	p->left = l->right;
	l->right = p;
	
	return l;
} 

 
 
 
 

Left Single Turn (L)

BiTree L_Revolve(BiTree p){//Left Single Rotation on Binary Sort Tree Rooted with p 
	BiTree l;
	l = p->right;
	p->right = l->left;
	l->left = p;
	
	return l; 
}

 
 
 
 

Left-right double turn (LR)

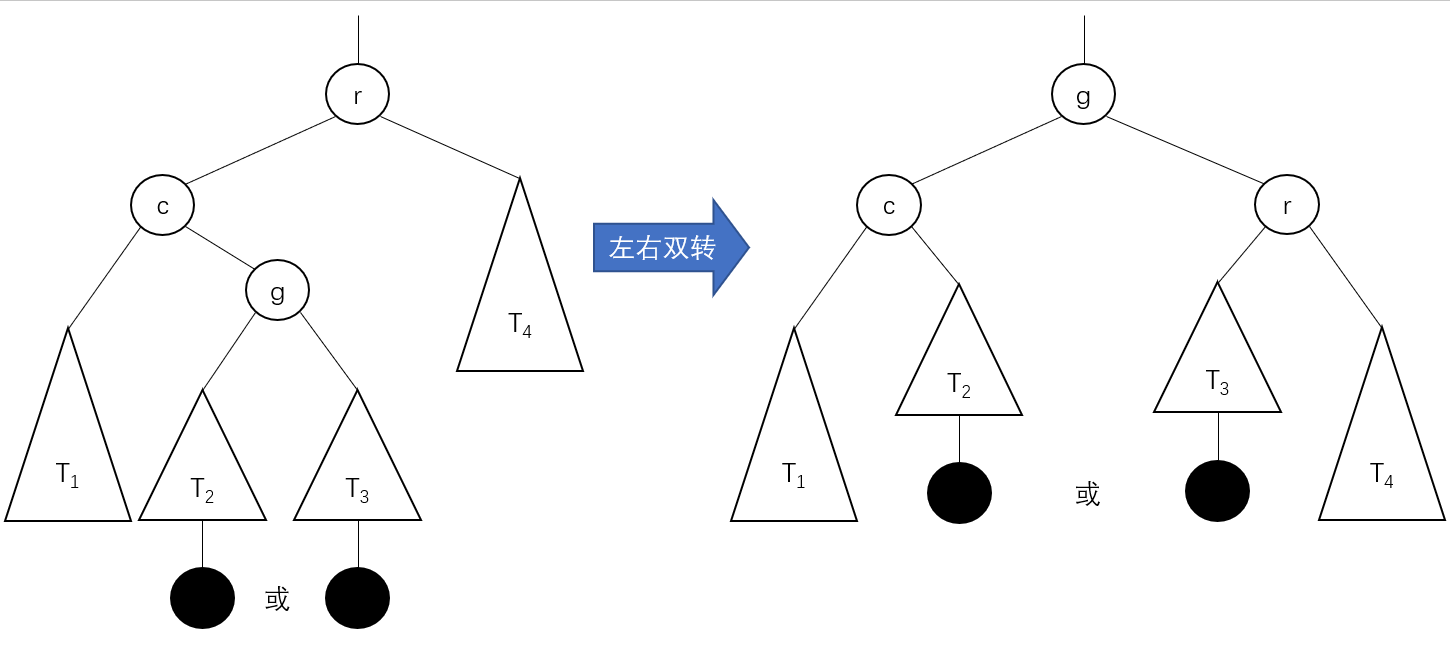
It's actually left-handed, then right-handed.

BiTree LR_Revolve(BiTree p){//Double-turn left and right for a binary sorting tree rooted in p 
	BiTree l;
	l = p->left;
	p->left = L_Revolve(l);
	return R_Revolve(p);
}

 
 
 
 

Right-Left Double Turn (RL)

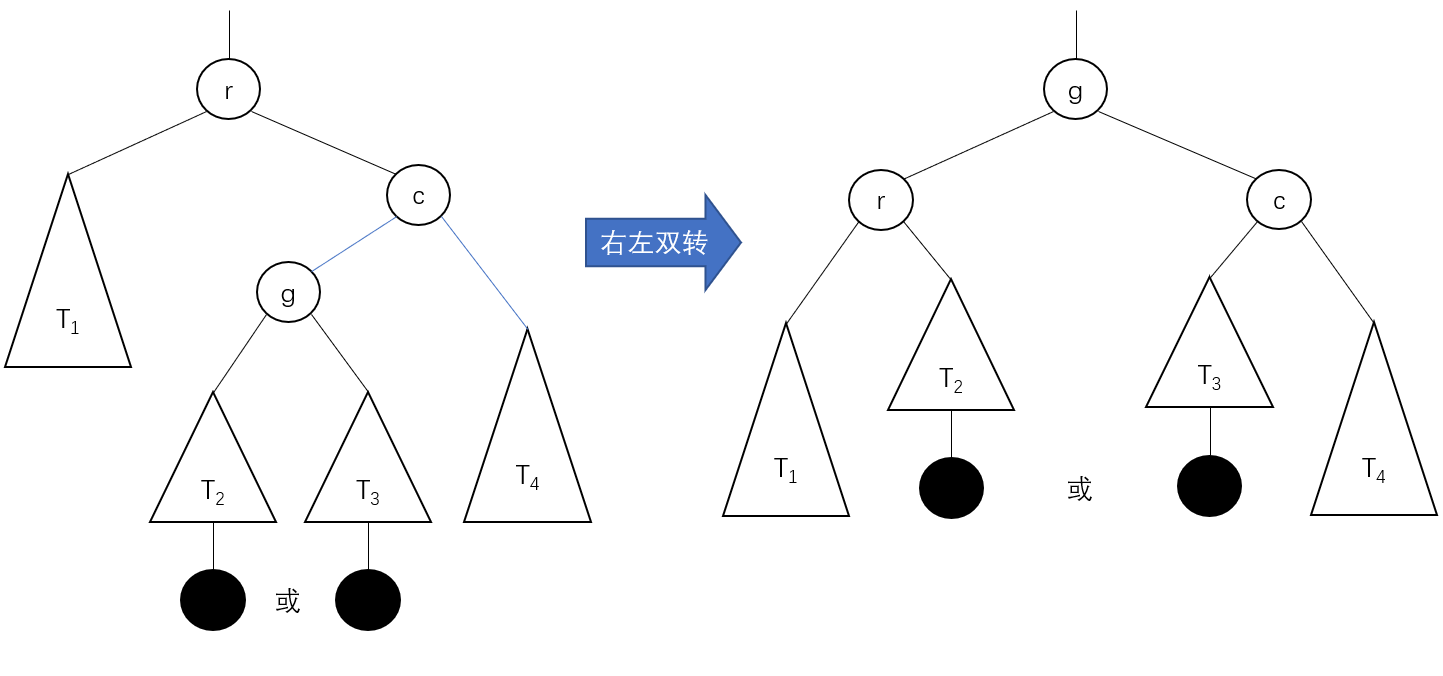
It's actually right-handed, then left-handed.

BiTree RL_Revolve(BiTree p){//Make right-left double turns on a binary sorted tree rooted in p 
	BiTree l;
	l = p->right;
	p->right = R_Revolve(l);
	return L_Revolve(p); 
}

 
 
 
 

insert

typedef struct Node
{
    int key;//Node Data
    struct Node *left;//left child
    struct Node *right;//Right Child
    int bf;//Balance factor
}BTNode, *BiTree;

int height(BiTree p){//Finding the height of a tree 
	if(p == NULL)
		return 0;
	int l = height(p->left);
	int r = height(p->right);
	return l > r ? l+1:r+1;
}

int getBF(BiTree p){//Finding the Balance Factor of p Nodes 
	if(p == NULL)
		return 0;
	return height(p->left) - height(p->right);
}

BiTree newNode(int key){//Create a new node with key data 
	BiTree p = (BiTree)malloc(sizeof(BTNode));
	p->key = key;
	p->left = NULL;
	p->right = NULL;
	p->bf = 0;
	return p;
}

BiTree R_Revolve(BiTree p){//Right Single Rotation on Binary Sort Tree Rooted with p
	BiTree l;
	l = p->left;
	p->left = l->right;
	l->right = p;
	
	return l;
} 

BiTree L_Revolve(BiTree p){//Left Single Rotation on Binary Sort Tree Rooted with p 
	BiTree l;
	l = p->right;
	p->right = l->left;
	l->left = p;
	
	return l; 
}

BiTree LR_Revolve(BiTree p){//Double-turn left and right for a binary sorting tree rooted in p 
	BiTree l;
	l = p->left;
	p->left = L_Revolve(l);
	return R_Revolve(p);
}

BiTree RL_Revolve(BiTree p){//Make right-left double turns on a binary sorted tree rooted in p 
	BiTree l;
	l = p->right;
	p->right = R_Revolve(l);
	return L_Revolve(p); 
}

BiTree insertNode(BiTree L, int key){//Insert a Node 
	if(L == NULL)
		return newNode(key);
	
	if(key < L->key)
		L->left = insert(L->left, key);
	else if(key > L->key)
		L->right = insert(L->right, key);
	else
		return L;
	
	L->bf = getBF(L);
	
	if(L->bf > 1 && key < L->left->key)//R-type
		return R_Revolve(L);
	
	if(L->bf < -1 && key > L->right->key)//L-type
		return L_Revolve(L);
	
	if(L->bf > 1 && key > L->left->key)//LR Type
		return LR_Revolve(L);
	
	if(L->bf < -1 && key < L->right->key)//RL Type
		return RL_Revolve(L);
	
	return L; 
}

 
 
 
 

delete

BiTree minKeyNode(BiTree p){//Find the smallest node in the tree 
	BiTree q = p;
	while(q->left != NULL)
		q = q->left;
	
	return q;
}

BiTree deleteNode(BiTree L, int key){//Delete Node 
	if(L == NULL)//Tree is empty 
		return L;
	
	if(key < L->key)//Data smaller than current node, go to left subtree to continue 
		L->left = deleteNode(L->left, key);
	else if(key > L->key)//Data larger than current node, go to right subtree to continue 
		L->right = deleteNode(L->right, key);
	else{//Find deleted nodes 
		if(L->left == NULL || L->right == NULL){//Left and right subtrees are empty at different times 
			BiTree p = L->left ? L->left : L->right;
			
			if(p == NULL){//Both left and right subtrees are empty 
				p == L;
				L = NULL;
			}
			else//A subtree is empty 
				L = p;
		}
		else{//Both left and right subtrees exist 
			BiTree p = minKeyNode(L->right);//Find the minimum value in the right subtree to replace this point 
			L->key = p->key;
			L->right = deleteNode(L->right, p->key);//Then delete the point in the right subtree 
		}
	}
	
	if(L == NULL)
		return L;
	
	L->bf = getBF(L);
	
	if(L->bf > 1 && getBF(L->left) >= 0)//R-type
		return R_Revolve(L);
	
	if(L->bf < -1 && getBF(L->right) <= 0)//L-type
		return L_Revolve(L);
	
	if(L->bf > 1 && getBF(L->left) < 0)//LR Type
		return LR_Revolve(L);
	
	if(L->bf < -1 && getBF(L->right) > 0)//RL Type
		return RL_Revolve(L);
	
	return L; 
}

 
 
 
 

2-3 Trees

Summary

_A 2-3 search tree is either an empty tree or consists of the following nodes:

• A 2-node contains a key (and its corresponding value) and two links. The left link points to a key in the 2-3 tree that is smaller than the node, and the right link points to a key in the 2-3 tree that is larger than the node.
• A 3-node contains two keys (and their corresponding values) and three links. The keys in the 2-3 tree that the left link points to are smaller than the node. The keys in the 2-3 tree that the middle link points to are between the two keys of the node, and the keys in the 2-3 tree that the right link points to are larger than the node.
  

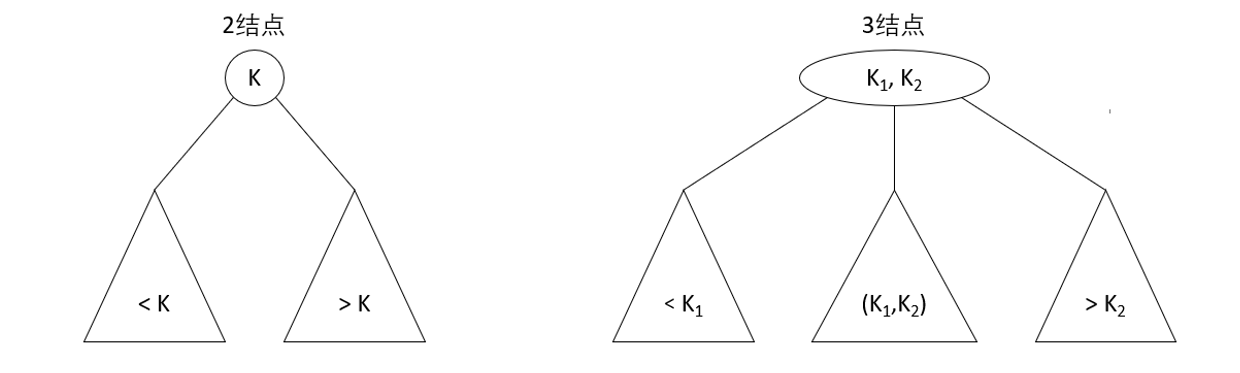
The last requirement of a 2-3 tree is that all the leaves in the tree must be on the same level, that is, a 2-3 tree is always highly balanced: for each leaf, the path length from the root to the leaf is the same.
 
 
 
 

lookup

_Finding a given key K in a 2-3 tree is very simple, similar to finding a binary sorted tree.
_starts from the root. If the root is a 2-node, we treat it as a binary sort tree: if K equals the key value of the root, the algorithm stops; If K is less than or greater than the root key value, we continue to look in the left subtree or the right subtree, respectively. If the root is a three-node, after no more than two comparisons, you will know whether to stop the search (K equals a key value of the root) or continue to look in which of the three subtrees of the root.
 
 
 
 

insert

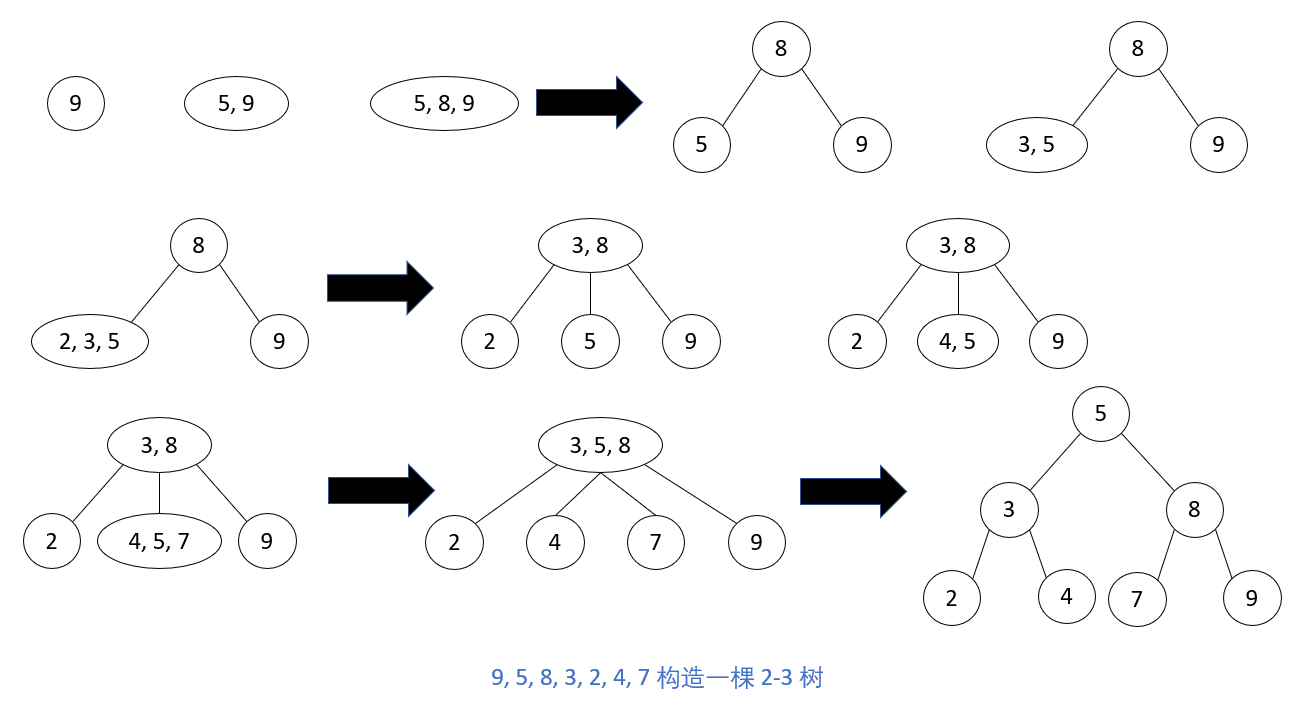
Firstly, we always insert a new key K into a leaf unless the tree is empty.
_We determine a suitable insertion position by looking for K. If the leaf found is a 2-node, we insert K as the first or second key, depending on whether K is smaller or larger than the original key in the node. If the found leaf is a three-node, we divide the leaf into two nodes: the smallest of the three keys (two original keys and one new key) is placed in the first leaf and the largest in the second. At the same time, the middle key is promoted to the parent of the original leaf (if the leaf happens to be the root of the tree, we create a new root to accept the middle key). Note that elevation of the middle key to the parent may cause the parent to overflow (if it is a 3-node) and, therefore, multiple nodes to split along the ancestor chain of the leaf.

 
 
 
 

delete

Deletion is divided into three cases:

1. Remove non-leaf nodes
2. Delete leaf nodes that are not 2-node
3. Delete 2-node leaf nodes

 

 
 
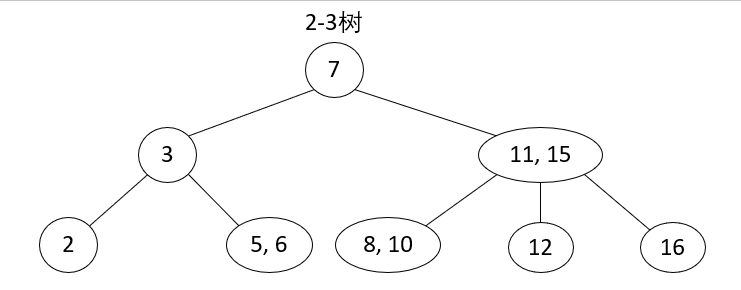
Remove non-leaf nodes
Existing steps: Use the left most key of the right child to overwrite the key of the node currently to be deleted, and then delete the key value to be overwritten.

 
 
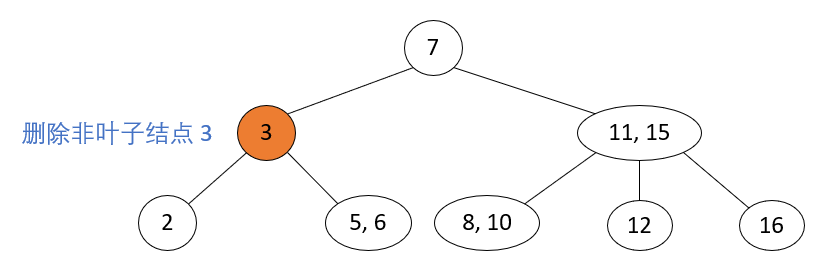
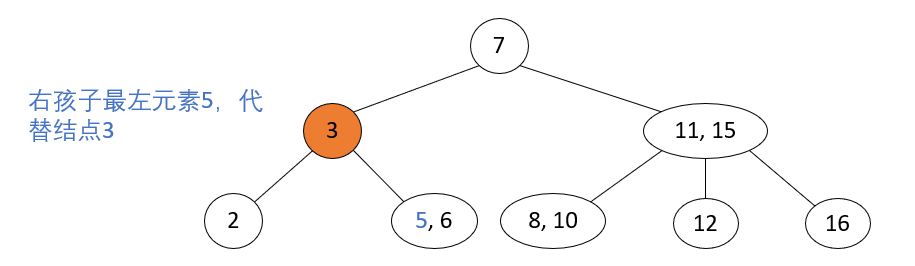
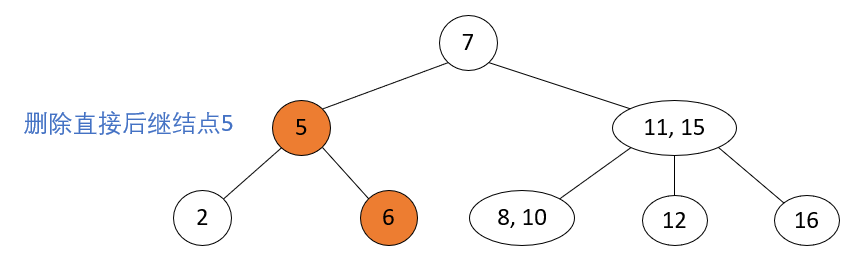
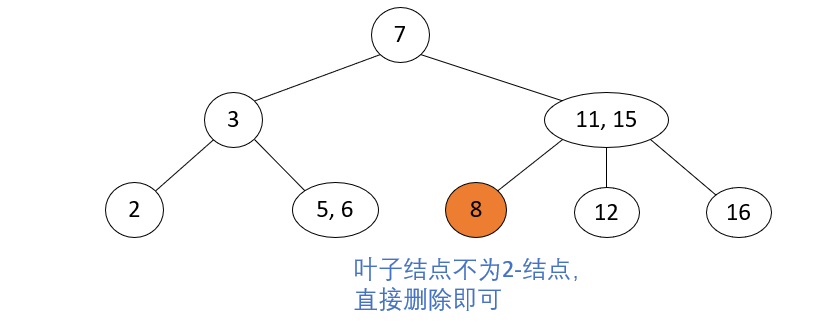
Delete leaf nodes that are not 2-nodes
Operation steps: Delete leaf nodes that are not 2-node, and delete nodes directly.


 
 
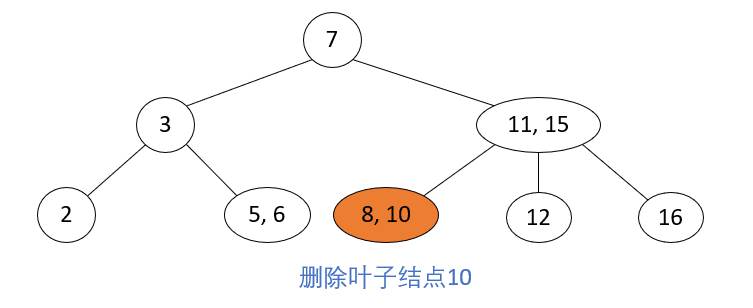
Delete 2-node leaf nodes
There are four cases:

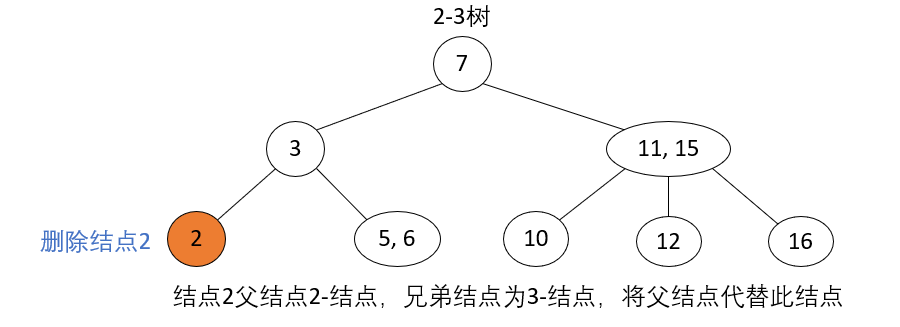
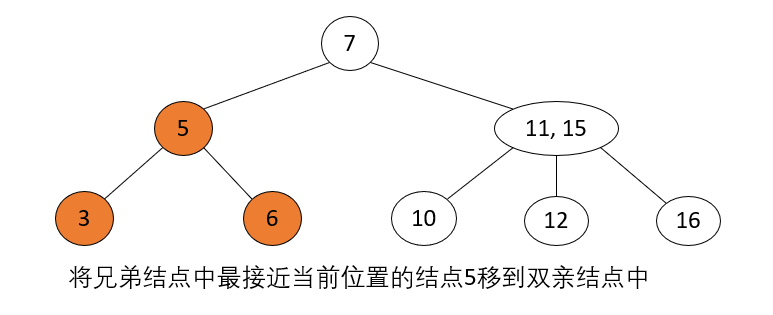
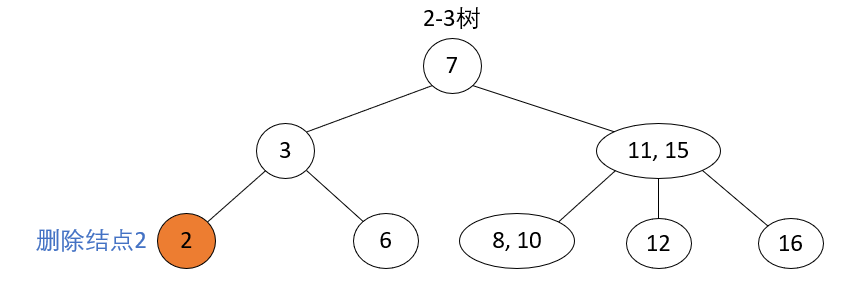
1. Delete Node 2-Node, Parent 2-Node, Brother 3-Node
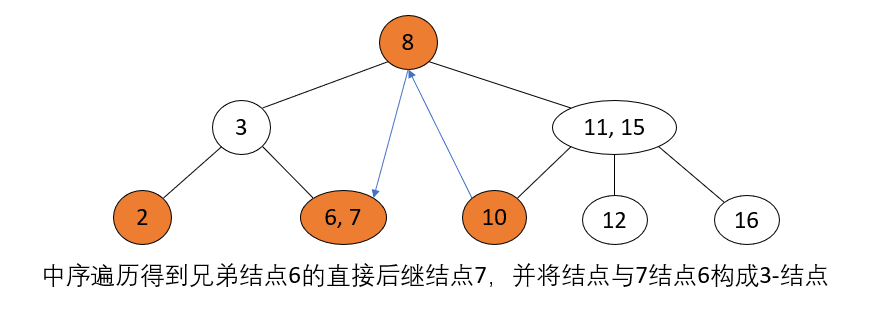
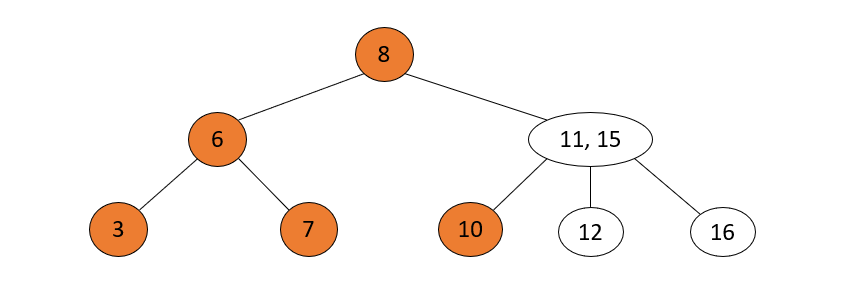
   _Operation steps: The parent node of the current node to be deleted is 2-node, the sibling node is 3-node, move the parent node to the current location of the node to be deleted, and move the key closest to the current location in the sibling node to the parent node.
   
   

2. Delete Node 2-Node, Parent 2-Node, Brother 2-Node
   _Operation steps: The parent node of the current node to be deleted is 2-node, and the sibling node is 2-node, which is traversed directly to the sibling node by moving the sibling node in the middle order, so that the sibling node becomes 3-node; Do 1 more.
   
   
   

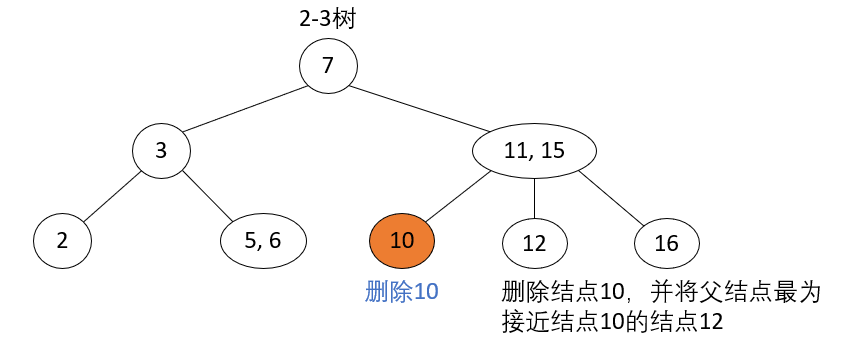
3. Delete node 2-node, parent 3-node
   _Operation steps: The parent node of the current node to be deleted is a 3-node, the parent node is split to make it a 2-node, the closest split key in the parent node is merged with the child, and the merged node is used as the current node.
   
   

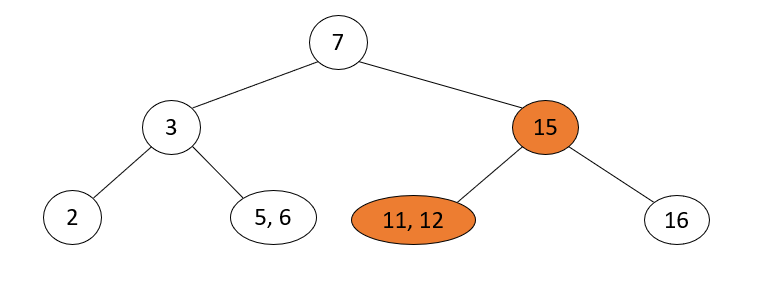
4. 2-3 trees are full binary trees, remove leaf nodes
   _Operation steps: If the 2-3 tree is a full binary tree, reduce the 2-3 tree layer tree, merge the sibling nodes that currently delete the node into the parent node, and merge all the sibling nodes of the parent node into the parent node. If the 4-node is generated, then decompose the 4-node.
   
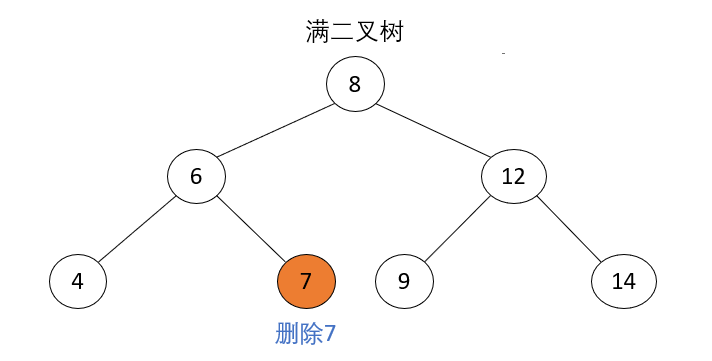
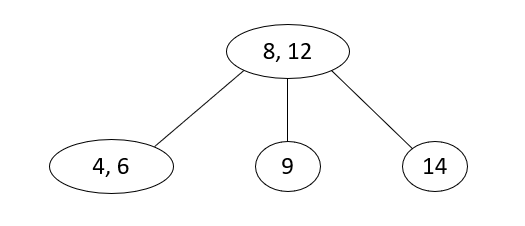
   _2-3 trees are full binary trees, reducing the number of layers of 2-3 trees, moving brothers node 4 up to parent node 7, and all brothers node 12 of parent node 7 up to parent node 8 of parent node.
   

 
 
 
 

Analysis

_A 2-3 tree with n keys and a height of h.
log ⁡ 3 ( n + 1 ) − 1 ≤ h ≤ log ⁡ 2 ( n + 1 ) − 1 \log _{3}\left( n+1\right) -1\leq h\leq \log _{2}\left( n+1\right) -1 log3​(n+1)−1≤h≤log2​(n+1)−1
So in the worst case or in general, the time efficiency of finding, inserting, and deleting 2-3 trees is O(logn).
 
 
 
 

2-3-4 tree

Summary

_A 2-3-4 search tree is either an empty tree or consists of the following nodes:

• A 2-node contains a key (and its corresponding value) and two links. The left link points to a key in the 2-3-4 tree that is smaller than the node, and the right link points to a key in the 2-3-4 tree that is larger than the node.
• A 3-node contains two keys (and their corresponding values) and three links. The keys in the 2-3-4 tree that the left link points to are smaller than the node. The keys in the 2-3-4 tree that the middle link points to are between the two keys of the node, and the keys in the 2-3-4 tree that the right link points to are larger than the node.
• A 4-node contains three keys (and their corresponding values) and four links. The keys in the 2-3-4 tree that the first link points to are smaller than the node. The keys in the 2-3-4 tree that the second link points to are between the first two keys of the node. The keys in the 2-3-4 tree that the third link points to are between the last two keys of the node. The fourth link points to keys in the 2-3-4 tree that are larger than the node.
  
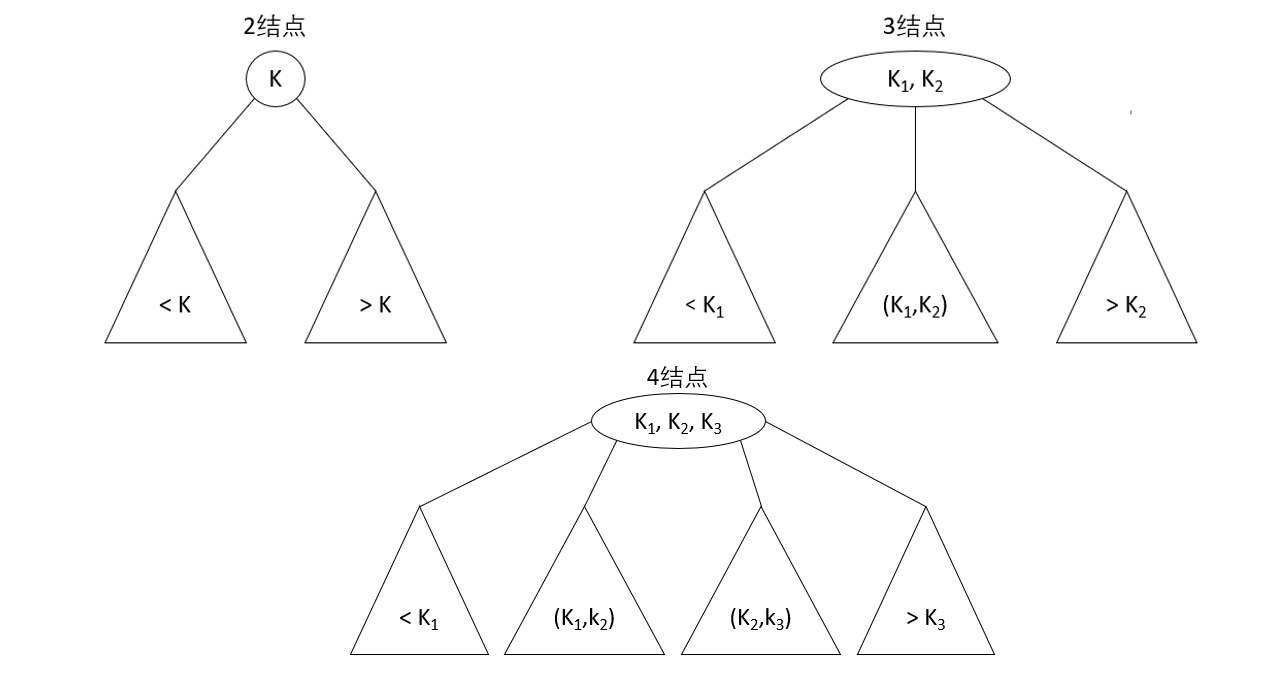
  The last requirement of a 2-3-4 tree is that all the leaves in the tree must be in the same layer, that is, a 2-3-4 tree is always highly balanced: for each leaf, the path length from the root to the leaf is the same.
   
   
   
   

lookup

Finding a given key K in a 2-3-4 tree is very simple, similar to finding a binary sorted tree.
_starts from the root. If the root is a 2-node, we treat it as a binary sort tree: if K equals the key value of the root, the algorithm stops; If K is less than or greater than the root key value, we continue to look in the left subtree or the right subtree, respectively. If the root is a three-node, after no more than two comparisons, you will know whether to stop the search (K equals a key value of the root) or continue to look in which of the three subtrees of the root. If the root is a 4-node, after no more than three comparisons, you will know whether to stop the search (K equals a key value of the root) or continue the search in which of the four subtrees of the root.
 
 
 
 

insert

Firstly, we always insert a new key K into a leaf unless the tree is empty.
_We determine a suitable insertion position by looking for K. If the leaf found is a 2-node or 3-node, we use K as a key according to whether K is smaller or larger than the original key in the node.