catalogue
1,LeetCode——1748. Sum of unique elements
2,LeetCode——387. The first unique character in the string
3,LeetCode——1941. Check that all characters appear the same number of times
4,LeetCode——448. Find all missing numbers in the array
5,LeetCode——1512. Number of good pairs
1,LeetCode-1748. Sum of unique elements
I'll give you an integer array {nums. The only elements in the array are those that appear exactly once.
Please return the sum of the unique elements in {num}.
Tips:
- 1 <= nums.length <= 100
- 1 <= nums[i] <= 100
Example 1:
Input: num = [1,2,3,2] Output: 4 Explanation: the only elements are [1,3], and 4.
Example 2:
Input: num = [1,1,1,1,1] Output: 0 Explanation: there is no unique element, and is 0.
Example 3:
Input: num = [1,2,3,4,5] Output: 15 Explanation: the only element is [1,2,3,4,5], and is 15.
Idea: because the maximum number of data is 100, and there is at least one, and because the size of data elements is between 1-100, you can create an array with the size of 101 to store the occurrence times of 100 numbers from 1-100. Finally, traverse the array to find the number with the occurrence times of 1 and add it.
Code and details:
int sumOfUnique(int* nums, int numsSize){
int arr[101]; //Count array
memset(arr,0,sizeof(arr)); //Initialize array
int sum=0; //and
for(int i=0;i<numsSize;i++){ //First find out all the numbers that have appeared
++arr[nums[i]]; //Plus means the number of times plus one
}
for(int i=1;i<=100;i++){ //Starting from 1, because the elements in nums are greater than or equal to 1, the position with subscript 0 is useless
if(arr[i]==1) //The number of occurrences is 1
sum+=i; //accumulation
}
return sum;
}2,LeetCode-387. The first unique character in a string
Given a string, find its first non repeating character and return its index. If it does not exist, - 1 is returned.
Assume all lowercase letters
Example:
s = "leetcode" Return 0 s = "loveleetcode" Return 2
Idea: find the first non repeating character, use the counting method, first record the occurrence times of each character, and then find the character with the occurrence times of 1 and return the subscript. You can count with an array of size 26, because there are only 26 English letters.
Code and details:
int firstUniqChar(char * s){
int len=strlen(s);
int count[26]; //Because there are only 26 lowercase letters
memset(count,0,sizeof(count));//initialization
//First record the number of times each character appears
for(int i=0;i<len;i++){
count[s[i]-'a']++;
}
//Find the character with 1 times again and return the subscript
for(int i=0;i<len;i++){
if(count[s[i]-'a']==1)
return i;
}
return -1;
}3,LeetCode-1941. Check whether all characters appear the same number of times
Give you a string "s". If "s" is a good string, please return true. Otherwise, please return false.
If all characters in s appear the same number of times, we call the string s a good string.
All lowercase letters are assumed
Example 1:
Input: s = "abacbc" Output: true Explanation: the characters that have appeared in s are 'a', 'b' and 'c'. All characters in s appear twice.
Example 2:
Input: s = "aaabb"
Output: false
Explanation: the characters that have appeared in s are 'a' and 'b' A 'appears 3 times and' b 'appears 2 times. The two appear at different times.
Idea: similar to the previous question, use an array with a size of 26 to store the number of occurrences of each character. Finally, cycle through it. If the number of occurrences is different, return false.
Code and details
bool areOccurrencesEqual(char * s){
int count[26]; //Count array
memset(count,0,sizeof(count)); //Initialize array
int len=strlen(s); //String length
for(int i=0;i<len;i++){ //Count the number of occurrences
++count[s[i]-'a'];
}
//Mode 1:
// For (int i = 0; I < 26; I + +) {/ / compare whether the occurrence times are the same
// if(count[s[0]-'a']!=count[i]&&count[i]!=0)
// return false;
// }
//Mode 2:
for(int i=0;i<len-1;i++){ //Compare whether the occurrence times are the same
if(count[s[i]-'a']!=count[s[i+1]-'a'])
return false;
}
return true;
}4,LeetCode-448. Find all missing numbers in the array
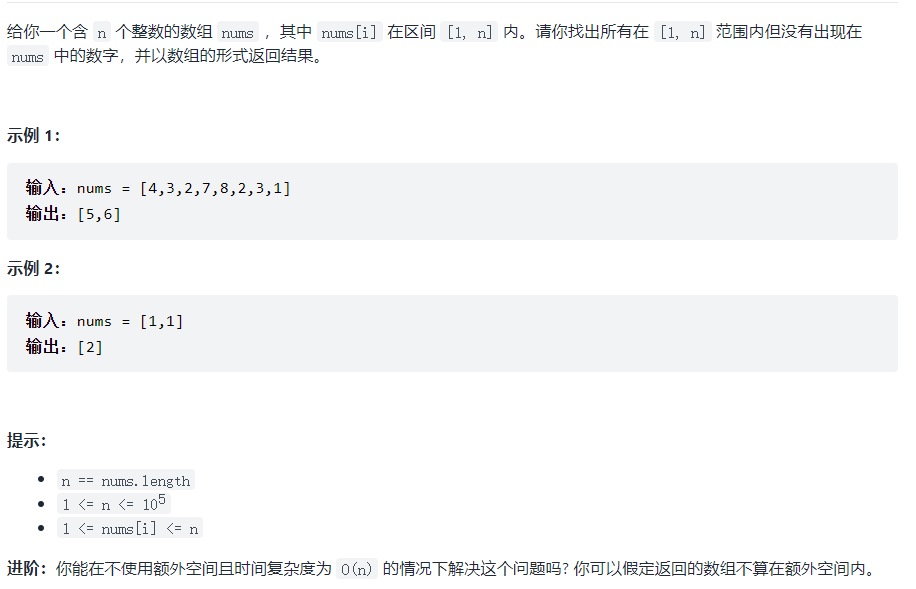
Idea: use a size of num The count array of length is used to count whether each digit has appeared, and then traverse the array to judge whether there is a position of 0. If there is any, the subscript is the number that disappears.
Code and details:
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){
int count[numsSize+1]; //Count array
int* res=(int*)malloc(sizeof(int)*numsSize); //Returned array
int j=0;
memset(count,0,sizeof(count)); //Initialize count array
for(int i=0;i<numsSize;i++){ //Record the number that appears
++count[nums[i]];
}
for(int i=1;i<=numsSize;i++){ //Save numbers that do not appear in the res array
if(count[i]==0)
res[j++]=i;
}
*returnSize=j; //Size of array
return res;
}5,LeetCode-1512. Number of good pairs
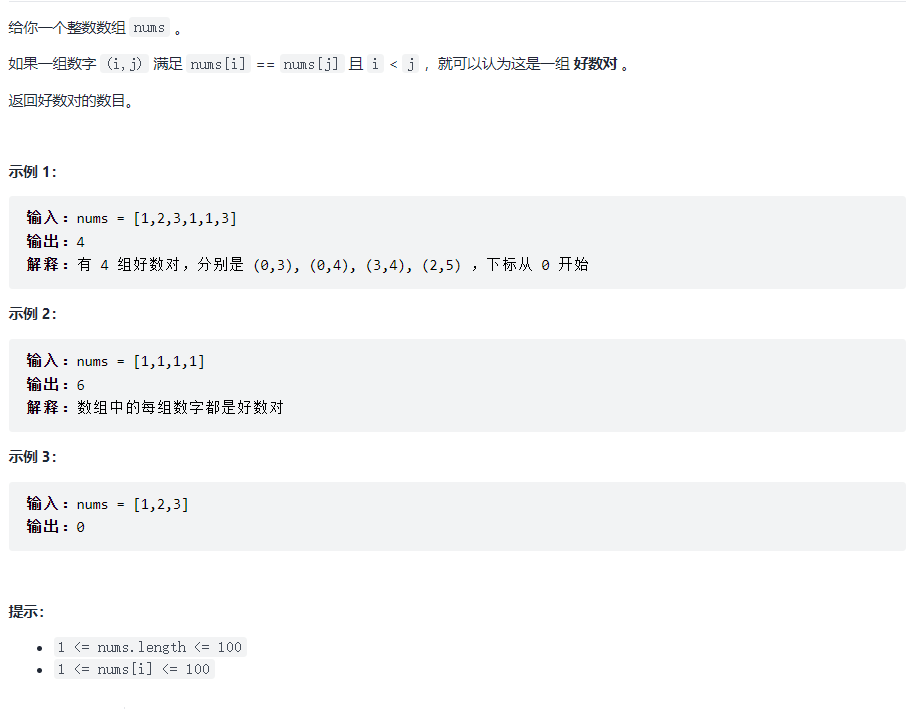
Idea: the title means to calculate the number of permutations of repeated numbers. If a number appears n times, there will be Cn2 good number pairs, so you still need to know how many times it is repeated.
Codes and details are as follows:
int numIdenticalPairs(int* nums, int numsSize){
int count[101]; //Count array
int sum=0;
memset(count,0,sizeof(count)); //Initialize array
for(int i=0;i<numsSize;i++){ //Record the number of occurrences
++count[nums[i]];
}
for(int i=0;i<101;i++){ //Judge the number of occurrences greater than 1
if(count[i]>1){
sum+=count[i]*(count[i]-1)/2;
}
}
return sum;
//Double cycle violence
//int count=0;
// for(int i=0;i<numsSize;i++){
// for(int j=0;j<numsSize;j++){
// if(nums[i]==nums[j]&&i<j)
// count++;
// }
// }
// return count;
}6,LeetCode-1711. Feast count
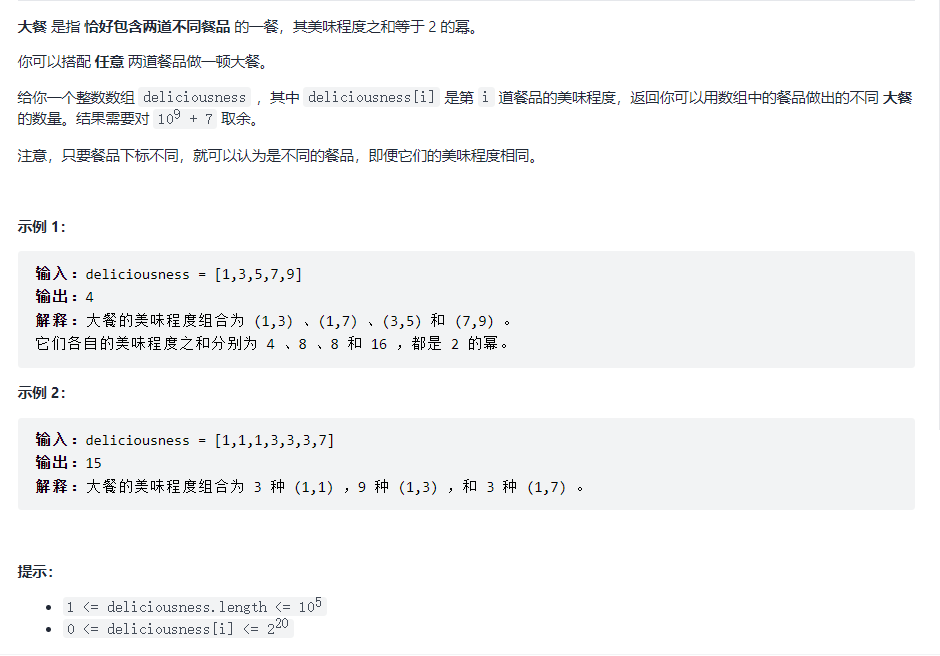
Idea: the meaning of the question is to find several logarithms in an array that can add up to the power of 2. According to the prompt, the maximum element in the array = 2 ^ 20, so the maximum sum of the two numbers = 2 ^ 21, so the number that meets the requirements of the question must be: 2 ^ 0, 2 ^ 1, 2 ^ 2 Between 2 ^ 20 and 2 ^ 21.
We can enumerate a number x, then enumerate their sum, and then get another number other: other=sum-x; Then accumulate the occurrence times of other in the array, and finally return the cumulative sum of% 1000000007.
Code and details:
int countPairs(int* deliciousness, int deliciousnessSize){
int count[(1<<21)+1]; //Count array
memset(count,0,sizeof(count)); //Initialize array
int ans,other; //ans is the result
for(int i=0;i<deliciousnessSize;i++){ //Traversing elements in an array
for(int sum=1;sum<=(1<<21);sum*=2){ //Enumerate each result. Because the result is a power of 2, sum multiplies 2 at a time
other=sum-deliciousness[i]; //You can cite other s
if(other<0)
continue;
//The existence of other indicates that it can form a big meal with the current delicacy [i], but it requires that other is an element in the array, so the number of results should be added to the number of occurrences of other in the array
ans+=count[other];
ans%=1000000007;
}
++count[deliciousness[i]]; //Record the occurrence times of this number. The operation here is to record the occurrence times
}
return ans;
}