[Algorithmic Basics Lesson] 1. Basic Algorithms (Top)] Quick Sort, Merge Sort, Binary

1. Basic Algorithms (Top)

1.1 Quick Sort

step

1. Determine the demarcation point: x = q[l] / x = q[(l + r) / 2] / x = q[r] / random
2. Adjust range:
   
3. Recursive processing on left and right ends

Template

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

Example

785. Quick Sort
Give you an integer column of length n.

Please use Quick Sort to sort this column from smallest to largest.

And output the sorted columns in order.

Input Format
The input consists of two lines, the first containing the integer n.

The second line contains n integers (all in 1 ∼ 1 0 9 1∼10^9 1_109), representing the entire array.

Output Format
The output is a row of n integers representing an ordered column.

Data Range
1 ≤ n ≤ 100000 1 ≤ n ≤ 100000 1≤n≤100000

Input sample:
5
3 1 2 4 5
Output sample:
1 2 3 4 5

#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int q[N];

void quick_sort(int q[], int l, int r) {
    if (l >= r) return;
    
    int x = q[(l + r) / 2], i = l - 1, j = r + 1;
    
    while (i < j) {
        while (q[++i] < x);
        while (q[--j] > x);
        
        if (i < j) swap(q[i], q[j]);
    }
    
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }
    
    quick_sort(q, 0, n - 1);
    
    for (int i = 0; i < n; i++) {
        printf("%d ", q[i]);
    }
    
    return 0;
}

1.2 Merge Sort

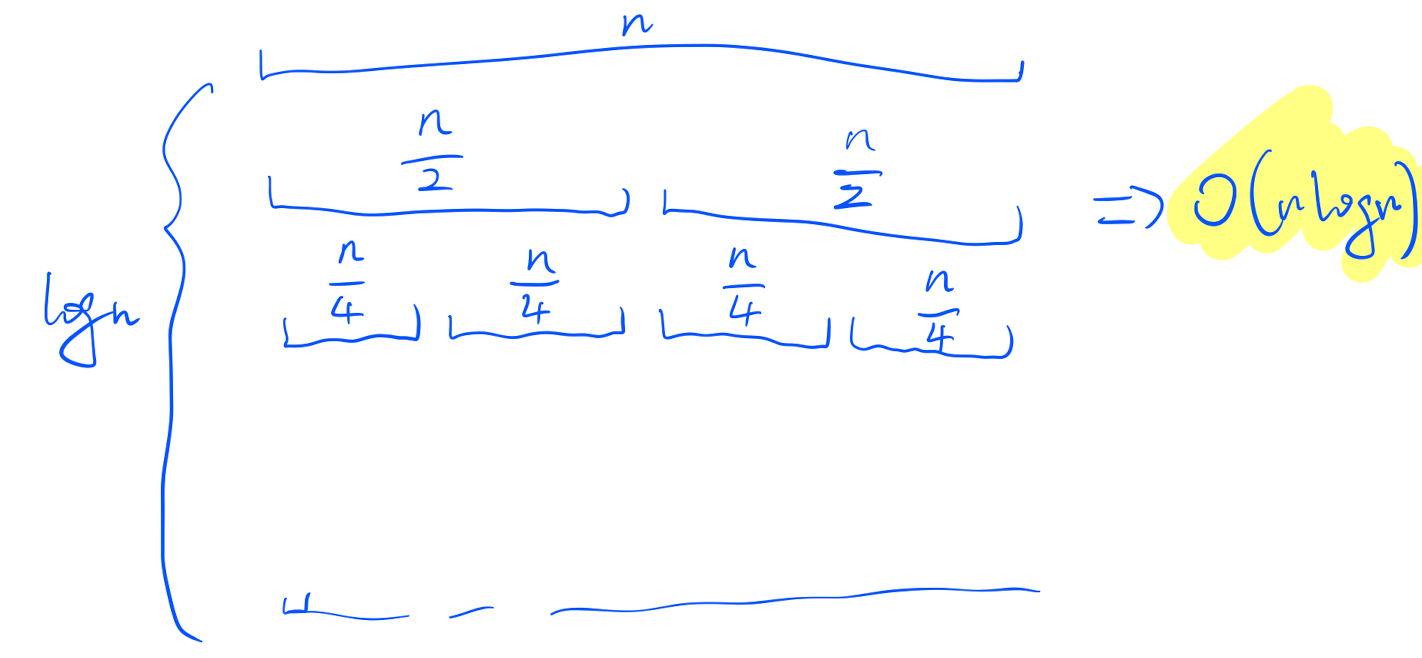
step

1. Establish boundaries: mid = (l + r) / 2
2. Recursive sort left, right
3. Merge - merge into one [complexity of O(n)]
   

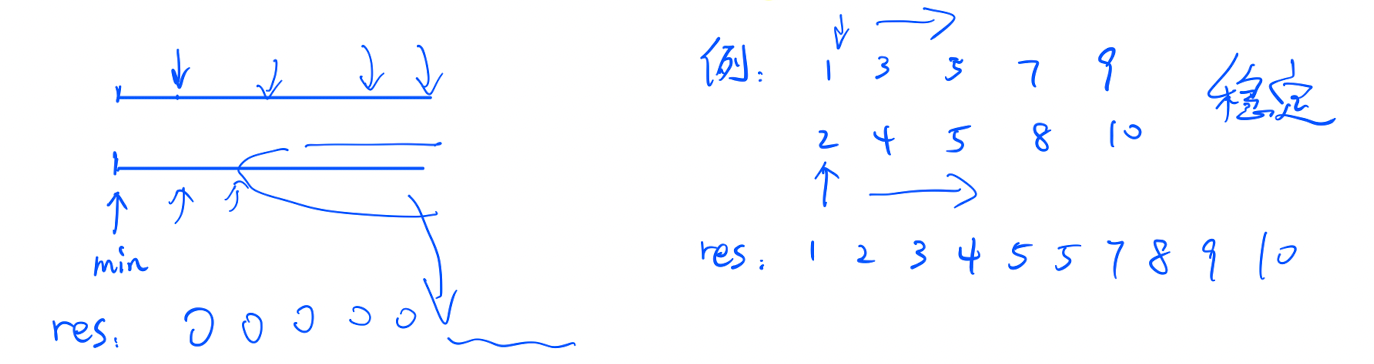
Template

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

Example

787. Merge Sort
Give you an integer column of length n.

Please use merge sort to sort this column from smallest to largest.

And output the sorted columns in order.

Input Format
The input consists of two lines, the first containing the integer n.

The second line contains n integers (all in 1 ∼ 1 0 9 1∼10^9 1_109), representing the entire array.

Output Format
The output is a row of n integers representing an ordered column.

Data Range
1 ≤ n ≤ 100000 1≤n≤100000 1≤n≤100000

Input sample:
5
3 1 2 4 5
Output sample:
1 2 3 4 5

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 100010;

int n;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r) {
    if (l >= r) return;
    
    int mid = (l + r) / 2;
    
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r) {
        if (q[i] < q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    
    for (i = l, j = 0; i <= r; i++, j++) {
        q[i] = tmp[j];
    }
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);
    
    merge_sort(q, 0, n - 1);
    
    for (int i = 0; i < n; i++) printf("%d ", q[i]);
    
    return 0;
}

1.3 - 1 dichotomy (integer)

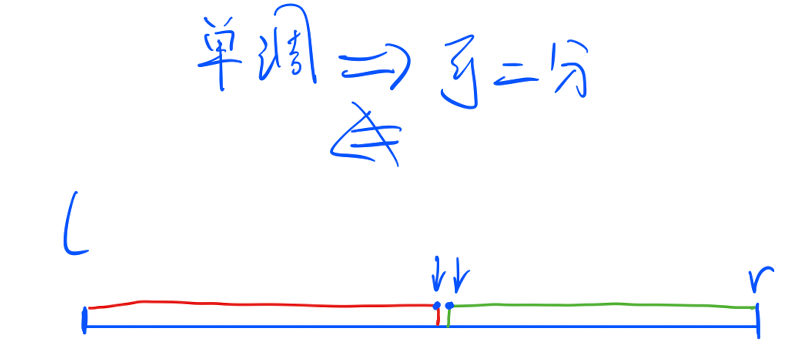
step

Template

bool check(int x) {/* ... */} // Check if x satisfies a certain property

// The intervals [l, r] are divided into [l, mid] and [mid + 1, r] using:
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check() to determine if mid satisfies a property
        else l = mid + 1;
    }
    return l;
}
// The intervals [l, r] are divided into [l, mid-1] and [mid, r]:
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

Example

The range of 789.
Given an integer array of length n in ascending order, and q queries.

For each query, the start and end positions of an element k are returned (positions count from 0).

Returns -1-1 if the element does not exist in the array.

Input Format
The first line contains the integers n and q, representing the length of the array and the number of queries.

The second line contains n integers (all in the range 1_10000) representing the complete array.

The next q lines, each containing an integer k, represent a query element.

Output Format
There are q rows, each containing two integers representing the starting and ending positions of the elements.

Returns -1-1 if the element does not exist in the array.

Data Range
1 ≤ n ≤ 100000 1≤n≤100000 1≤n≤100000
1 ≤ q ≤ 10000 1≤q≤10000 1≤q≤10000
1 ≤ k ≤ 10000 1≤k≤10000 1≤k≤10000

Input sample:
6 3
1 2 2 3 3 4
3
4
5
Output sample:
3 4
5 5
-1 -1

#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int q[N];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);
    
    while(m--) {
        int x;
        scanf("%d", &x);
        
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (q[mid] >= x) r = mid;
            else l = mid + 1;
        }
        
        if (q[r] != x) cout << "-1 -1" << endl;
        else {
            cout << r << " ";
            
            int l = 0, r = n - 1;
            while (l < r) {
                int mid = l + r + 1>> 1;
                if (q[mid] <= x) l = mid;
                else r = mid - 1;
            }
            
            cout << r << endl;
        }
    }
    
    return 0;
}

1.3 - 2 dichotomy (floating point number)

step

The floating-point dichotomy procedure is similar to but simpler than integer, with no need to consider +1 or -1.

Template

bool check(double x) {/* ... */} // Check if x satisfies a certain property

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps denotes accuracy, depending on the subject's requirements for accuracy
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

Example

The cubic root of 790.
Given a floating-point number n, find its cubic root.

Input Format
A row containing a floating-point number n.

Output Format
A row containing a floating point number that represents the solution to the problem.

Note that the result retains 6 decimal places.

Data Range
− 10000 ≤ n ≤ 10000 −10000≤n≤10000 −10000≤n≤10000

Input sample:
1000.00
Output sample:
10.000000

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 10010;

double n;

int main() {
    scanf("%lf", &n);
    double l = -10000, r = 10000;
    while (r - l > 1e-8) {
        double mid = (l + r) / 2;
        if (mid * mid * mid >= n) r = mid;
        else l = mid;
    }
    
    printf("%.6lf", r);
    
    return 0;
}