preface

Preparation basis Xiuyan teacher's Brochure Combined with leetcode Binary tree of sword finger offer Learn this part.

Non recursive implementation of first order, second order, middle order and sequence traversal

In my understanding, a tree is a special kind of graph. The first order corresponds to the depth traversal of the graph, while the sequence corresponds to the breadth traversal of the graph.

The recursive implementation of first order and second order is still relatively easy to understand. For non recursive implementation, manually implement a recursive stack.

When I first learned the data structure, I followed the mooc of Zhejiang University. There is a well understood explanation for the traversal of trees:

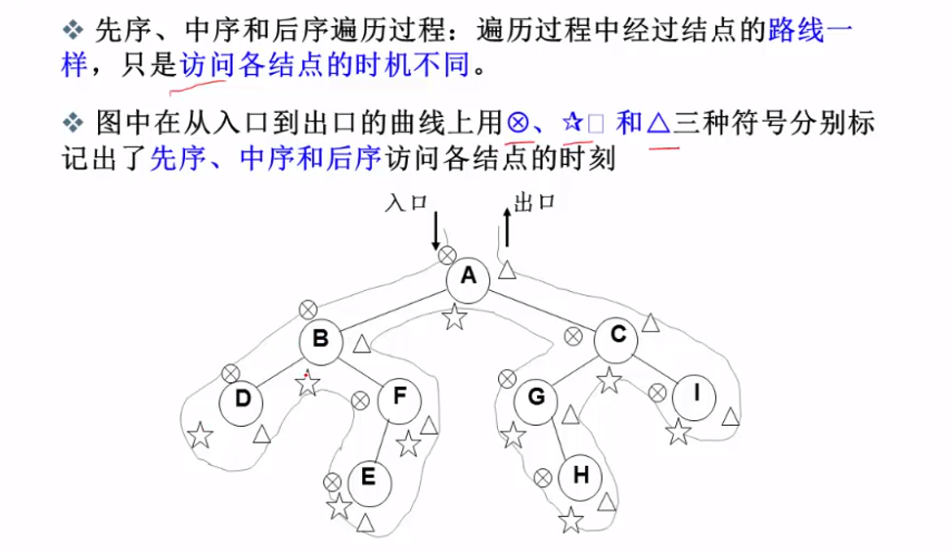
The order read out according to the cross is the pre order traversal, which happens to pass through the node for the first time

The order read out according to the asterisk is the middle order traversal, which happens to pass through the node for the second time

The order read out according to the triangle is post order traversal, which happens to pass through the node for the third time

 

ok draw not much on ~ on the code

Preorder traversal

We need to pay attention to a stack order of the stack array.

As we all know, the (x) priority is the order of root = > left = > right ~ so when entering the stack, you should first right and then left to ensure that the left is always accessed first when bouncing the stack.

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const preorderTraversal = function(root) {
  // Define result array
  const res = []  
  // Dealing with boundary conditions
  if(!root) {
      return res
  }
  // Initialize stack structure
  const stack = [] 
  // First, put the root node into the stack
  stack.push(root)  
  // If the stack is not empty, repeat the operations of out stack and in stack
  while(stack.length) {
      // Record the top node of the stack as the current node
      const cur = stack.pop() 
      // The current node is the root node of the current subtree. Put this node at the end of the result array
      res.push(cur.val)
      // If the root node of the current subtree has a right child, the right child will be put into the stack
      if(cur.right) {
          stack.push(cur.right)
      }
      // If the root node of the current subtree has a left child, the left child will be put into the stack
      if(cur.left) {
          stack.push(cur.left)
      }
  }
  // Return result array
  return res
};

 

Postorder traversal

Hey, in fact, post order traversal and pre order traversal are still very similar!

As we all know, the order after (x) is ， left = > right = > root

When traversing, we will always access the root first.

So there is a good way. Before, we added a val at the end of the res array. In the post order, you can add a val at the head of the res array instead. (equivalent to changing res from a queue to a stack)

Correspondingly, originally considering the stack, we always put right at the bottom of the stack and left at the top of the stack.

This idea will be reversed when traversing in the later order. We should press left first and then right~

This will also be popped out first and pushed into the res array. The order of ~ res will become: left = > right = > root

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const postorderTraversal = function(root) {
  // Define result array
  const res = []  
  // Dealing with boundary conditions
  if(!root) {
      return res
  }
  // Initialize stack structure
  const stack = [] 
  // First, put the root node into the stack
  stack.push(root)  
  // If the stack is not empty, repeat the operations of out stack and in stack
  while(stack.length) {
      // Record the top node of the stack as the current node
      const cur = stack.pop() 
      // The current node is the root node of the current subtree. Put this node at the head of the result array
      res.unshift(cur.val)
      // If the root node of the current subtree has a left child, the left child will be put into the stack
      if(cur.left) {
        stack.push(cur.left)
      }  
      // If the root node of the current subtree has a right child, the right child will be put into the stack
      if(cur.right) {
        stack.push(cur.right)
      }
  }
  // Return result array
  return res
};

Middle order traversal

Compared with the first two similar traversal methods, the middle order traversal is somewhat out of place (x)

As we all know, the order in (x) is the order of {left = > root = > right

Code idea:
While (stack non null 𞓜 pointer non null):
Stack the left subtree of all// Include root node
Outbound access;
The pointer points to the right node

This also has the advantage that when accessing out of the stack, the root point is actually accessed. Then, right will be put on the stack to ensure the traversal order~

 

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const inorderTraversal = function(root) {
  // Define result array
  const res = []  
  // Initialize stack structure
  const stack = []   
  // Using a cur node as a cursor
  let cur = root  
  // When cur is not empty or stack is not empty, repeat the following logic
  while(cur || stack.length) {
      // The function of this while is to record all nodes of the path in the process of finding the leftmost leaf node 
      while(cur) {
          // Stack the nodes of the path
          stack.push(cur)  
          // Continue to search the left child of the current node
          cur = cur.left  
      }
      // Take out the top element of the stack
      cur = stack.pop()  
      // Put the top element on the stack
      res.push(cur.val)  
      // Try to read the right child of cur node
      cur = cur.right
  }
  // Return result array
  return res
};

level traversal

Xiuyan teacher quoted a question here about sequence traversal. I think sequence traversal is relatively simple. It's easy to understand by looking at the code directly~

Title Description: give you a binary tree. Please return the node values obtained by traversing in sequence. (that is, access all nodes from left to right layer by layer).

 

/**
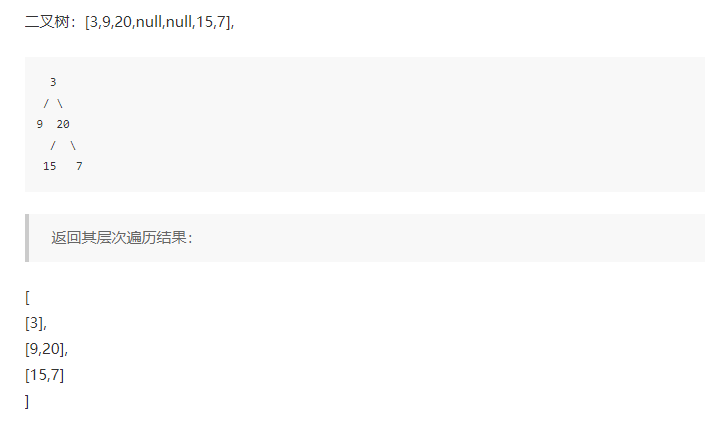
 * @param {TreeNode} root
 * @return {number[][]}
 */
const levelOrder = function(root) {
    // Initialize result array
    const res = []  
    // Dealing with boundary conditions
    if(!root) {
        return res
    }  
    // Initialize queue
    const queue = []   
    // The first element of the queue is the root node
    queue.push(root)  
    // When the queue is not empty, repeat the following logic
    while(queue.length) {
        // level is used to store the nodes of the current layer
        const level = []  
        // Cache the queue length when it first enters the loop. This step is critical because the queue length will change later
        const len = queue.length  
        // Loop through the nodes of the current level
        for(let i=0;i<len;i++) {
            // Fetch the header element of the queue
            const top = queue.shift()  
            // Push the value of the header element into the level array
            level.push(top.val)
            // If the current node has left children, it will be pushed to the next level
            if(top.left) {
                queue.push(top.left)
            }
            // If the current node has a right child, push it to the next level
            if(top.right) {
                queue.push(top.right)
            }
        }
        // Push level into result array
        res.push(level)
    }
    // Return result array
    return res
};

 

Sword finger offer

Recently, I was brushing my sword finger offer with classmate Zhou according to the tag. The progress is one question a day. Recently, I found that the lc mobile phone version is easy to use. I can use my mobile phone to brush questions during the subway and lunch break~

Sword finger Offer 27 Image of binary tree

The problem was finished without looking at the teacher's pamphlet.

The idea is also very simple: recursively, traverse each node in the tree, and exchange the left and right children of each node.

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var mirrorTree = function(root) {
     //Define recursive boundaries
      if(root) {
        //Swap left and right subtrees
        let tmp = root.left
        root.left = root.right
        root.right = tmp
        //recursion
        mirrorTree(root.left)
        mirrorTree(root.right)

        return root
      }else {
        return root
      }
};

Sword finger Offer 28 Symmetric binary tree

It is also a recursive problem.

Because it is to judge symmetry, from the root node, whether the left is equal to the right.

If equal to, judge:

1. Is the left node of the left node equal to the right node of the right node

2. Is the right node of the left node equal to the left node of the right node

var isSymmetric = function(root) {
    return check(root, root)
};

const check = (leftPtr, rightPtr) => {
    // Returns true if there is only a root node
    if (!leftPtr && !rightPtr) return true
    // If there is only one left and right node, false is returned
    if (!leftPtr || !rightPtr) return false
    
    return leftPtr.val === rightPtr.val && check(leftPtr.left, rightPtr.right) && check(leftPtr.right, rightPtr.left)
}

Sword finger Offer 37 Serialized binary tree

I've used this question

//serialize
var serialize = function(root) {
    let res=[]
    let queue=[root]
    while(queue.length){
        let node=queue.shift()
        if(node){
            res.push(node.val)
            queue.push(node.left)
            queue.push(node.right)
        }else{
            res.push('X')
        }
    }
    return res.join(',')
};

//Deserialization
var deserialize = function(data) {
      if (data == 'X') return null;
      
      // Serialize string split into array
      const list = data.split(',');  
      // Get the first item and build the root node
      const root = new TreeNode(list[0]); 
      // Root node push queue
      const queue = [root];
      // Initial point to the second item of the list          
      let cursor = 1;                
      // The pointer is out of bounds, that is, the serialized string is swept
      while (cursor < list.length) {  
         // Examine the nodes of the column
        const node = queue.shift(); 
         // The value of its left son
        const leftVal = list[cursor]; 
        // The value of its right son    
        const rightVal = list[cursor + 1]; 

     // Judge whether it is a real node
    if (leftVal != 'X') {              
      const leftNode = new TreeNode(leftVal); 
      node.left = leftNode;                  
      queue.push(leftNode);                  
    }

    if(rightVal != 'X'){
        const rightNode = new TreeNode(rightVal);
        node.right=rightNode;
        queue.push(rightNode);
    }
   // Visit a pair of sons at a time and add 2 to the pointer
    cursor += 2; 
      }
   return root; 
};