Basic concept of stack

Before we start, let's still think about a few questions:

1. What are some examples of stacks in life?

2. What problems do you think stack can solve in practical development?

Previously, we talked about two basic implementations of linear tables, sequential storage and chain storage. Now we add a constraint to the basic operation of this linear table, as shown in the figure below.

Insert and delete operations are only allowed at one end of the table.

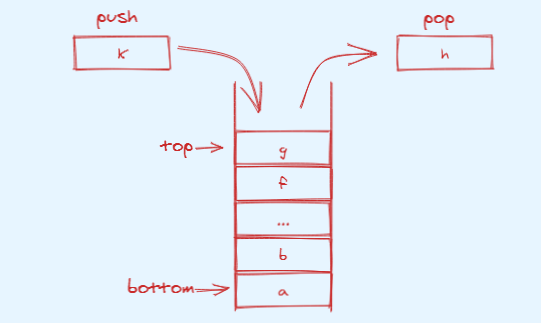
Linear tables with this feature are called "stack", the top of the table is called "top", and the bottom of the table is called "bottom". Each time we only operate on the top of the stack, it has the characteristics of first in, last out, last in, first out, which is abbreviated as FIFO. There are many examples of stack in our life. For example, when putting dishes, the last one is always on the top; Another example is to walk through the maze, always try to go forward first, there is no way at the end, and then go back to the nearest place to explore other exits. There are also many applications in software, such as judging whether the operation expression is compliant, syntax analysis in Compilation Principle and so on.

Before implementing stack related operations, we introduce a mathematical property related to stack. n different elements are put on the stack in order, and the number of out of stack elements in different order can be calculated according to the following formula. This formula is called Catalan number:

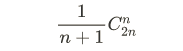
Specific proof can refer to combinatorial mathematics textbooks or Wikipedia.

Implementation of stack

• Sequential storage structure

// Static memory allocation is adopted
#define MAX_SIZE 100
typedef int ElemType;
typedef struct {
    ElemType data[MAX_SIZE];
    int top // Stack top pointer
} SqStack;
// The method of dynamic memory allocation is adopted. When the storage space of the stack is not enough, a piece of memory is reallocated
#define INIT_SIZE 100
#define INCREMENT 20
typedef struct {
    ElemType *bottom;
    ElemType *top;
    int stackSize;
} SqStack;

In order to facilitate the operation, we use the statically allocated array to realize the related manipulation.

// We assume that the initial position of the stack top pointer is - 1, and top points to the stack top element
// initialization
bool InitStack(SqStack *stack) {
    stack->top = -1;
    return true;
}
// Judge empty stack
bool EmptyStack(SqStack *stack) {
    return stack->top == -1 ? true : false;
}
// Judge full stack
bool FullStack(SqStack *stack) {
    return stack->top == MAX_SIZE-1 ? true : false;
}
// Stack operation
bool PushStack(SqStack *stack, ElemType data) {
    if (FullStack(stack)) {
        printf("stack full\n");
        return false;
    }
    
    stack->data[++stack->top] = data;
    return true;
}

// Out of stack operation
bool PopStack(SqStack *stack, Elemtype *data) {
    if (EmptyStack(stack)) {
        printf("stack empty\n");
        return false;
    }
    
    *data = stack->data[stack->top--];
    return true;
}

The method of dynamic memory allocation is similar to the basic operation in the previous section, which will not be repeated here. For details, please refer to the textbook data structure (C language version) by Yan Weimin and WU Weimin. Next, we implement the basic operation of the stack through the chain structure.

• Linked Storage Structure

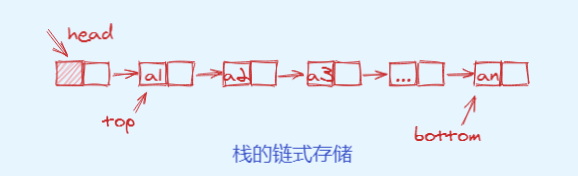
typedef int ElemType;
typedef struct LinkNode
{
    ElemType data;
    struct LinkNode *next;
} *LinkStack;

// Judge empty stack
bool EmptyStack(LinkStack linkStack)
{
    return linkStack->next == NULL ? true : false;
}

// Judge full stack (chain structure omitted)

// Push 
bool PushStack(LinkStack linkStack, ElemType data)
{
    if (linkStack == NULL)
    {
        return false;
    }
    struct LinkNode *newNode = (struct LinkNode*)malloc(sizeof(struct LinkNode));
    if (newNode == NULL)
    {
        return false;
    }
    newNode->data = data;
    newNode->next = NULL;

    newNode->next = linkStack->next;
    linkStack->next = newNode;

    return true;
}

// Out of stack
bool PopStack(LinkStack linkStack, ElemType *data)
{
    if (linkStack == NULL || linkStack->next == NULL)
    {
        return false;
    }

    struct LinkNode *tmpNode = linkStack->next;
    *data = tmpNode->data;
    linkStack->next = tmpNode->next;

    return true;
}

Linked list operation application

• The reversal of the linked list (supplement the application of the second linked list operation), as shown in the figure below.

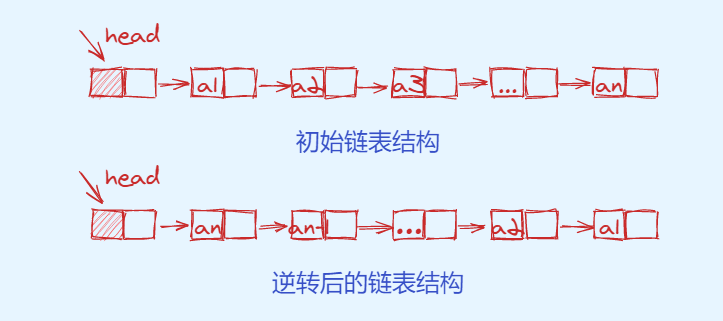
• Solution 1: we can traverse each node of the linked list one by one, and then insert the traversed node into the new linked list using the head insertion method (inserted from the head node) to realize the reversal of the linked list.

• Sample code

typedef int ElemType
typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
} *LinkList;

bool ReverseLinkList(LinkList Sq)
{
    // exception handling
    if (Sq == NULL)
    {
        return false;
    }

    LinkList tmpSq = Sq->next;
    LinkList tmpNode = NULL;
    LinkList tmpList = (LinkList)malloc(sizeof(struct LinkNode));
    if (tmpList == NULL)
    {
        return false;
    }
    tmpList->next = NULL;

    while (tmpSq != NULL)
    {
        tmpNode = tmpSq;
        tmpSq = tmpSq->next;

        // Insert header into new linked list
        tmpNode->next = tmpList->next;
        tmpList->next = tmpNode;
    }

    Sq->next = tmpList->next;
    free(tmpList);

    return true;
}

• Solution 2: optimize the previous solution

bool ReverseLinkList2(LinkList Sq)
{
    if (Sq == NULL)
    {
        return false;
    }

    LinkList newList = NULL;
    LinkList curNode = Sq->next;
    LinkList tmpNode = NULL;

    while ( curNode != NULL )
    {
        tmpNode = curNode;
        curNode = curNode->next;
        tmpNode->next = newList;
        newList = tmpNode;
    }

    Sq->next = newList;
    return true;
}

• Solution 3: adopt the idea of recursion

  The idea of recursion is to decompose a complex problem into two parts and deal with the two parts respectively. If the two parts are still very complex, decompose the two sub problems until they can be handled simply. In fact, we can hold the general idea of recursive implementation. According to my personal experience, the difficulty lies in the determination of recursive termination conditions and how to correctly transfer parameters to the upper layer to ensure the correct processing of recursion. The specific processing steps of linked list reverse recursive implementation are as follows.

  

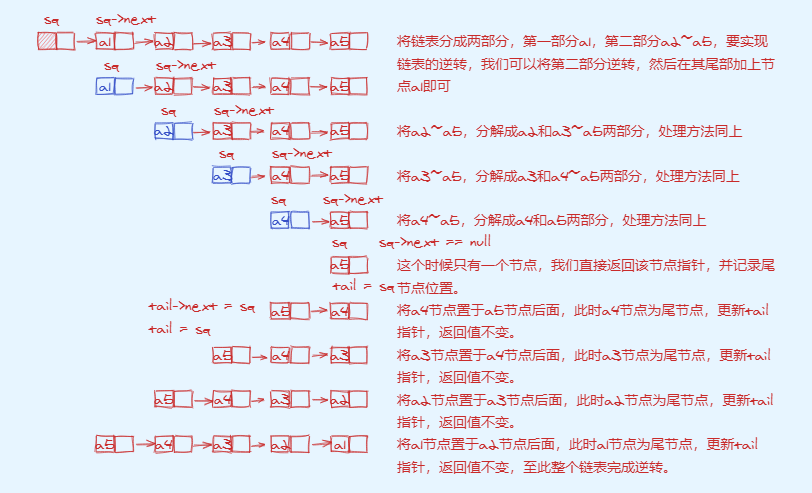
• Sample code

typedef int ElemType
typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
} *LinkList;

LinkList reverse(LinkList Sq, LinkList *tail)
{
    LinkList reversedSq = Sq;

    if(Sq->next == NULL)
    {
        *tail = Sq;
    }
    else
    {
        reversedSq = reverse(Sq->next, tail);
        (*tail)->next = Sq;
        *tail = Sq;
    }

    return reversedSq;
}

bool ReverseLinkList3(LinkList Sq)
{
    if (Sq == NULL)
    {
        return false;
    }

    LinkList *tail = (LinkList)malloc(sizeof(LinkList));
    Sq->next = reverse(Sq->next, tail);
    // This step cannot be less. Tail - > next in recursive functions always points to the previous node
    (*tail)->next = NULL;

    return true;
}

Application of stack in expression calculation

Let's first look at an arithmetic expression:

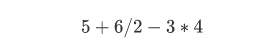
This arithmetic expression consists of two parts, operands and operators. Expressions can be divided into the following types according to the position of operands and operators.

Prefix expression - the operation symbol is before two operands; Infix expression - the operation symbol is between two operands; Suffix expression - the operand symbol is after two operands.

The above formula is infix expression. The corresponding prefix expression and suffix expression are:

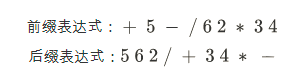
Infix expression is the expression that we can normally process and recognize. What people input in the computer is the form of infix expression, but this form is not easy to be processed by the computer. Therefore, to calculate the value of a given expression, our calculation program needs to convert infix expression into prefix expression or suffix expression for calculation. Let's talk about the calculation and conversion rules of these expressions.

Computers use prefix expressions to evaluate:

Scan the expression from right to left. If it is a numeric character, press that character into the stack. If it is an operator, pop up two operands from the stack. Calculate the result according to the order of OP at the top of the stack and then press it into the stack. Continue to scan the expression character string to the left and repeat the processing logic described above. The final calculated result is the value of the expression.

Example: calculate prefix expression: + 5 - / 6 2 * 3 4

1. Scan from right to left and press 4 and 3 into the stack;

2. When the * operator is encountered, pop up 3 and 4 (3 is the top element of the stack and 4 is the secondary top element), calculate the value of 3 * 4, and press 12 into the stack;

3. Press 2 and 6 into the stack;

4. When encountering the / operator, pop up 6 and 2 (6 is the top element of the stack and 2 is the secondary top element), calculate the value of 6 / 2 and press 3 into the stack;

5. When encountering the - operator, pop up 3 and 12 (3 is the top element of the stack and 12 is the secondary top element), calculate the value of 3-12 and press - 9 into the stack;

6. Push 5 into the stack

7. When encountering the + operator, pop up 5 and - 9 (5 is the top element of the stack and - 9 is the secondary top element), calculate the value of 5-9 and press - 4 into the stack;

8. After scanning, the value in the stack is taken out as the final result.

**The computer uses the suffix expression to evaluate: * * scan the expression from left to right. If it is a numeric character, push the character into the stack. If it is an operator, pop up two operands from the stack, calculate the result in the order of the secondary stack top element OP stack top element and push it into the stack; Continue to scan the value of the expression to the right, repeat the above processing logic, and the finally calculated value is the value of the expression.

Example: calculate suffix expression: 5 6 2 / + 3 4 *-

1. Scan from left to right and press 5, 6 and 2 into the stack;

2. When the / operator is encountered, 2 and 6 pop up (2 is the top element of the stack and 6 is the secondary top element. Note that it is compared with the prefix expression), calculate the value 3 of 6 / 2 and push it into the stack;

3. When encountering the + operator, pop up 3 and 5 (3 is the top element of the stack and 5 is the secondary top element), calculate the value 8 of 5 + 3 and push it into the stack;

4. Push 3 and 4 onto the stack

5. When the * operator is encountered, pop up 4 and 3 (4 is the top element of the stack and 3 is the secondary top element), calculate the value of 3 * 4, and press 12 into the stack;

6. Encounter the - operator, pop up 12 and 8 (12 is the top element of the stack and 8 is the secondary top element), calculate the value of 8-12, - 4 and press it into the stack;

7. After scanning, the value in the stack is taken out as the final result.

Infix expression, suffix expression and prefix expression are converted to each other

See you next time...

reference

[1] Data structure: C language version Yan Weimin et al Beijing: Tsinghua University Press, 2007

[2] Data structure Postgraduate Entrance Examination Review Guide: Kingway forum Electronic Industry Press

[3] Data structure: Second Edition Chen Yue Beijing: Higher Education Press

[4] Prefix, infix and suffix expressions: Antineutrino

For more knowledge, please pay attention to official account.