Basic concepts of pytoch
Tensor
Pytorch Tensor (Tensor) is the most basic operation object of Pytorch. Its English name is Tensor. It represents a multi-dimensional matrix. For example, zero dimension is a point, one dimension is a vector, two dimension is a general matrix, and multi dimension is equivalent to a multi-dimensional array, which corresponds to numpy. Moreover, Python's Tensor can be converted to numpy's darray. The only difference is that Python can run on GPU, while numpy's darray can only run on CPU.
Tensor s of different data types are commonly used as follows:
- 32-bit floating-point torch FloatTensor
- 64 bit floating point torch DoubleTensor
- 16 bit integer torch ShortTensor
- 32-bit integer torch IntTensor
- 64 bit integer torch LongTensor
Variable
Variable, that is, variable, which is not available in numpy, is a unique concept in the neural network calculation diagram, that is, variable provides the function of automatic derivation. Before, if you know Tensorflow, you should know that when neural network performs operations, you need to construct a calculation map first, and then run forward propagation and back propagation in it.
There is no difference between Variable and Tensor in essence, but Variable will be put into a calculation diagram, and then forward propagation, back propagation and automatic derivation will be carried out.
First, the Variable is in torch autograd. In variables, it is also very simple to turn a tensor into a Variable. For example, if you want to turn a tensor a into a Variable, you only need Variable(a). The properties of a Variable are as follows:

Variable has three important component attributes: data, grad and grad_fn. The tensor value in the variable can be retrieved through data, grad_fn indicates the operation to get this variable. For example, it is obtained by addition, subtraction or multiplication and division. Finally, grad is the back-propagation gradient of the variable.
When building variables, you should pay attention to passing in a parameter requires_grad=True, this parameter indicates whether to calculate the gradient of this Variable. The default is False, that is, do not calculate the gradient of this Variable. Here we want to obtain the gradient of these variables, so we need to pass this parameter.
y. The line of backward (), which is called automatic derivation, is actually equivalent to y.backward(torch.FloatTensor([1]). However, the parameters in scalar derivation can be omitted. For automatic derivation, you don't need to specify which function is derived from which function. You can directly derive all variables requiring gradient through this line of code, Get their gradients, and then get the gradient of x through x.grad.
Matrix derivation is equivalent to giving a three-dimensional vector for operation. At this time, the result y is a vector. Here, the derivation of this vector cannot be directly written as y.backward(), so the program will report an error. At this time, you need to pass in parameter declarations, such as y.backward (roach. Floattensor ([1, 1, 1]), so that the result is the gradient of each component, or you can pass in y.backward(torch.FloatTensor([1, 0.1, 0.01]), so that the gradient is their original gradient multiplied by 1, 0.1 and 0.01 respectively.
Data set
Data reading and preprocessing are the primary operations for machine learning. PyTorch provides many methods to complete data reading and preprocessing. This article introduces the simple usage of Dataset, TensorDataset, DataLoader and ImageFolder.
torch.utils.data.Dataset
torch.utils.data.Dataset is an abstract class representing this data. You can define your own data class, inherit and rewrite this abstract class, which is very simple. You only need to define__ len__ And__ getitem__ These two functions:
from torch.utils.data import Dataset
import pandas as pd
class myDataset(Dataset):
def __init__(self,csv_file,txt_file,root_dir, other_file):
self.csv_data = pd.read_csv(csv_file)
with open(txt_file,'r') as f:
data_list = f.readlines()
self.txt_data = data_list
self.root_dir = root_dir
def __len__(self):
return len(self.csv_data)
def __gettime__(self,idx):
data = (self.csv_data[idx],self.txt_data[idx])
return data
Through the above methods, we can define the data classes we need, and obtain each data through iteration, but it is difficult to obtain batch, shuffle or Multithread to read data.
torch.utils.data.TensorDataset
torch.utils.data.TensorDataset inherits from Dataset, and the new version replaces the previous data_tensor and target_ The tensor is removed, and the input becomes a variable parameter, that is, we usually use * args.
How to use the original train_dataset = Data.TensorDataset(data_tensor=x, target_tensor=y) # How to use the new version train_dataset = Data.TensorDataset(x,y)
For the TensorDataset method, refer to the following example:
import torch
import torch.utils.data as Data
BATCH_SIZE = 5
x = torch.linspace(1, 10, 10)
y = torch.linspace(10, 1, 10)
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
dataset=torch_dataset,
batch_size=BATCH_SIZE,
shuffle=True,
num_workers=0,
)
for epoch in range(3):
for step, (batch_x, batch_y) in enumerate(loader):
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ', batch_x.numpy(), '| batch y: ', batch_y.numpy())
Execution results:

torch.utils.data.DataLoader
PyTorch provides a simple way to do this through torch utils. data. Dataloader to define a new iterator, as follows:
from torch.utils.data import DataLoader dataiter = DataLoader(myDataset,batch_size=32,shuffle=True,collate_fn=defaulf_collate)
The parameters are very clear, only collate_fn identifies how to take samples. We can define our own functions to accurately realize the desired functions. The default functions can be used in general.
It should be noted that the Dataset class is only equivalent to a packaging tool, which contains the address of the data. The real process of reading data into memory is carried out when the Dataloader performs batch iterative input.
torchvision.datasets.ImageFolder
In addition, in the torchvison package, there is a more advanced data reading class related to computer vision: ImageFolder. Its main function is to process pictures, and the pictures are required to be stored in the following form:
root/dog/xxx.png
root/dog/xxy.png
root/dog/xxz.png
root/cat/123.png
root/cat/asd/png
root/cat/zxc.png
Then call this class as follows:
from torchvision.datasets import ImageFolder dset = ImageFolder(root='root_path', transform=None, loader=default_loader)
Where root needs to be the root directory. There are several folders in this directory. Each folder represents a category: transform and target_transform is image enhancement, which will be described in detail later; Loader is the method of image reading, because we read the name of the image, and then convert the image into the image type we need through loader to enter the neural network.
PyTorch optimization
Optimization algorithm is a strategy to adjust the update of model parameters. In deep learning and machine learning, we often minimize or maximize the loss function by modifying parameters.
Optimization algorithms are divided into two categories:
(1) First order optimization algorithm
This algorithm uses the gradient value of each parameter to update the parameters. The most commonly used first-order optimization algorithm is gradient descent. The so-called gradient is the multivariable expression of the derivative. The gradient of the function forms a vector field and a direction. The directional derivative in this direction is the largest and equal to the gradient. The function of gradient descent is to find the minimum value, control the variance, update the model parameters, and finally make the model converge. The parameter update formula of the network is as follows:

(2) Second order optimization algorithm
The second-order optimization algorithm is used to minimize or maximize the loss function with the second-order derivative (also known as Hessian method). It is mainly based on Newton method, but this method is not widely used because of the high computational cost of the second-order derivative. torch.optim is a library that implements various optimization algorithms. Most common algorithms can be called directly through this package, and the interface has enough universality to integrate more complex methods in the future, such as random gradient descent, random gradient descent adding momentum, adaptive learning rate, etc. In order to build an optimizer, you need to give it an iterable containing the parameters to be optimized (which must all be Variable objects). Then set the parameter options of optimizer, such as learning rate, momentum, etc.
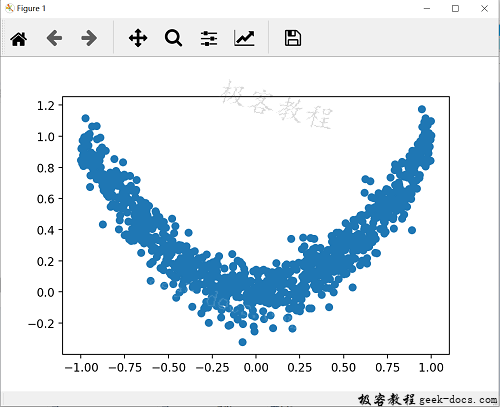
import torch import torch.utils.data as Data import torch.nn.functional as F from torch.autograd import Variable import matplotlib.pyplot as plt torch.manual_seed(1) # reproducible LR = 0.01 BATCH_SIZE = 32 EPOCH = 12 # fake dataset x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1) y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size())) # plot dataset plt.scatter(x.numpy(), y.numpy()) plt.show()
The results are as follows:
In order to compare each optimizer, we create a neural network for each optimizer, but this neural network comes from the same Net form. Next, create different optimizers to train different networks And create a loss_func is used to calculate the error. Several common optimizers: SGD, Momentum, RMSprop, Adam.
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=0,)
# Default network form
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
# Create a net for each optimizer
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # Record the loss of different neural networks during training
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (batch_x, batch_y) in enumerate(loader):
b_x = Variable(batch_x) # Be sure to wrap it with Variable
b_y = Variable(batch_y)
# For each optimizer, optimization belongs to his neural network
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get output for every net
loss = loss_func(output, b_y) # compute loss for every net
opt.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
opt.step() # apply gradients
l_his.append(loss.item()) # loss recoder
Training and loss drawing, the results are as follows:
